配对函数

在数学中，配对函数是唯一编码两个自然数到一个单一的自然数的过程。

在集合论中可以用任何配对函数来证明整数和有理数有同自然数相同的基数。在理论计算机科学中用它们把定义在自然数的向量上的函数 f:N^k → N 编码成一个新函数 g:N → N。

定义

配对函数是双射函数

$\pi :\mathbb {N} \times \mathbb {N} \to \mathbb {N}$ 。

康托尔配对函数

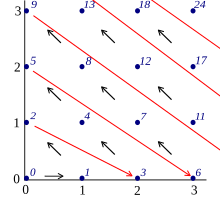康拖尔配对函数。

康托尔配对函数是配对函数

$\pi :\mathbb {N} \times \mathbb {N} \to \mathbb {N}$

定义为

$\pi (k_{1},k_{2}):={\frac {1}{2}}(k_{1}+k_{2})(k_{1}+k_{2}+1)+k_{2}.$

在应用配对函数到 $k_{1}$ 和 $k_{2}$ 的时候，我们经常指示结果的数为 $\langle k_{1},k_{2}\rangle$

这个定义可以归纳一般化为康托尔元组函数

$\pi ^{(n)}:\mathbb {N} ^{n}\to \mathbb {N}$

作为

$\pi ^{(n)}(k_{1},\ldots ,k_{n-1},k_{n}):=\pi (\pi ^{(n-1)}(k_{1},\ldots ,k_{n-1}),k_{n})$

引用

• Steven Pigeon. Pairing function. MathWorld.