第339行:
第339行:
|-
|-
|18
|18
|<math>\frac{1}{4}\sqrt[3]{4}\left(\sqrt[3]{i-\sqrt{3}}-\sqrt[3]{i+\sqrt{3}}\right)</math>
|<math>\frac{1}{4}\left(\sqrt[3]{4i -4 \sqrt{3}}-\sqrt[3]{4i +4 \sqrt{3}}\right)</math>
|<math>\frac{1}{4}\sqrt[3]{4}\left(\sqrt[3]{1+i\sqrt{3}}+\sqrt[3]{1-i\sqrt{3}}\right)</math>
|<math>\frac{1}{4}\left(\sqrt[3]{4 +4i \sqrt{3}}+\sqrt[3]{4 -4i \sqrt{3}}\right)</math>
|
|
|-
|-
2016年9月22日 (四) 15:32的版本
三角函數精確值 是利用三角函數的公式 將特定的三角函數 值加以化簡,並以數學根式 或分數 表示
用根式 或分數 表達的精確三角函數 有時很有用,主要用於簡化的解決某些方程式 能進一步化簡。
根据尼云定理 ,有理数度数的角的正弦值,其中的有理数仅有0,±1/2,±1。
注意 :以下為相同角度的轉換表:
相同角度的轉換表
角度單位
值
轉
0
{\displaystyle \mathbf {0} }
1
12
{\displaystyle {\tfrac {1}{12}}}
1
8
{\displaystyle {\tfrac {1}{8}}}
1
6
{\displaystyle {\tfrac {1}{6}}}
1
4
{\displaystyle {\tfrac {1}{4}}}
1
2
{\displaystyle {\tfrac {1}{2}}}
3
4
{\displaystyle {\tfrac {3}{4}}}
1
{\displaystyle \mathbf {1} }
角度
0°
30°
45°
60°
90°
180°
270°
360°
弧度
0
{\displaystyle \mathbf {0} }
π
6
{\displaystyle {\tfrac {\pi }{6}}}
π
4
{\displaystyle {\tfrac {\pi }{4}}}
π
3
{\displaystyle {\tfrac {\pi }{3}}}
π
2
{\displaystyle {\tfrac {\pi }{2}}}
π
{\displaystyle \pi }
3
π
2
{\displaystyle {\tfrac {3\pi }{2}}}
2
π
{\displaystyle 2\pi }
梯度
0
g
{\displaystyle 0^{g}}
33
1
3
g
{\displaystyle 33{\tfrac {1}{3}}^{g}}
50
g
{\displaystyle 50^{g}}
66
2
3
g
{\displaystyle 66{\tfrac {2}{3}}^{g}}
100
g
{\displaystyle 100^{g}}
200
g
{\displaystyle 200^{g}}
300
g
{\displaystyle 300^{g}}
400
g
{\displaystyle 400^{g}}
例如:0°、30°、45°
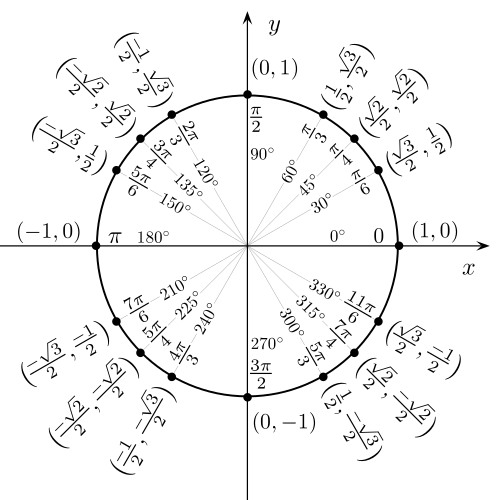
單位圓 例如:15°、22.5°
sin
(
x
2
)
=
±
1
2
(
1
−
cos
x
)
{\displaystyle \sin \left({\frac {x}{2}}\right)=\pm \,{\sqrt {{\tfrac {1}{2}}(1-\cos x)}}}
cos
(
x
2
)
=
±
1
2
(
1
+
cos
x
)
{\displaystyle \cos \left({\frac {x}{2}}\right)=\pm \,{\sqrt {{\tfrac {1}{2}}(1+\cos x)}}}
三倍角公式 求
1
3
{\displaystyle {\frac {1}{3}}\,}
例如:10°、20°、7°......等等,非三的倍數的角的精確值。
sin
3
θ
=
3
sin
θ
−
4
sin
3
θ
{\displaystyle \sin 3\theta =3\sin \theta -4\sin ^{3}\theta \,}
cos
3
θ
=
4
cos
3
θ
−
3
cos
θ
{\displaystyle \cos 3\theta =4\cos ^{3}\theta -3\cos \theta \,}
把它改為
sin
θ
=
3
sin
1
3
θ
−
4
sin
3
1
3
θ
{\displaystyle \sin \theta =3\sin {\frac {1}{3}}\theta -4\sin ^{3}{\frac {1}{3}}\theta \,}
cos
θ
=
4
cos
3
1
3
θ
−
3
cos
1
3
θ
{\displaystyle \cos \theta =4\cos ^{3}{\frac {1}{3}}\theta -3\cos {\frac {1}{3}}\theta \,}
把
cos
1
3
θ
{\displaystyle \cos {\frac {1}{3}}\theta \,}
cos
θ
{\displaystyle \cos \theta \,}
一元三次方程式 即可求出
例如:
sin
π
9
=
sin
20
∘
=
−
3
16
+
−
1
256
3
+
−
3
16
−
−
1
256
3
{\displaystyle \sin {\frac {\pi }{9}}=\sin 20^{\circ }={\sqrt[{3}]{-{\frac {\sqrt {3}}{16}}+{\sqrt {-{\frac {1}{256}}}}}}+{\sqrt[{3}]{-{\frac {\sqrt {3}}{16}}-{\sqrt {-{\frac {1}{256}}}}}}}
同樣地,若角度代未知數,則會得到三分之一角公式 。
cos
θ
n
=
ℜ
(
cos
θ
+
i
sin
θ
n
)
=
1
2
(
cos
θ
+
i
sin
θ
n
+
cos
θ
−
i
sin
θ
n
)
{\displaystyle \cos {\frac {\theta }{n}}=\Re \left({\sqrt[{n}]{\cos \theta +i\sin \theta }}\right)={\frac {1}{2}}\left({\sqrt[{n}]{\cos \theta +i\sin \theta }}+{\sqrt[{n}]{\cos \theta -i\sin \theta }}\right)}
sin
θ
n
=
ℑ
(
cos
θ
+
i
sin
θ
n
)
=
1
2
i
(
cos
θ
+
i
sin
θ
n
−
cos
θ
−
i
sin
θ
n
)
{\displaystyle \sin {\frac {\theta }{n}}=\Im \left({\sqrt[{n}]{\cos \theta +i\sin \theta }}\right)={\frac {1}{2i}}\left({\sqrt[{n}]{\cos \theta +i\sin \theta }}-{\sqrt[{n}]{\cos \theta -i\sin \theta }}\right)}
例如:
sin
1
∘
=
1
2
i
(
cos
3
∘
+
i
sin
3
∘
3
−
cos
3
∘
−
i
sin
3
∘
3
)
{\displaystyle \sin {1^{\circ }}={\frac {1}{2i}}\left({\sqrt[{3}]{\cos {3^{\circ }}+i\sin {3^{\circ }}}}-{\sqrt[{3}]{\cos {3^{\circ }}-i\sin {3^{\circ }}}}\right)}
=
1
4
2
3
i
{
[
2
(
1
+
3
)
5
+
5
+
2
(
5
−
1
)
(
3
−
1
)
]
+
i
[
2
(
1
−
3
)
5
+
5
+
2
(
5
−
1
)
(
3
+
1
)
]
3
{\displaystyle ={\frac {1}{4{\sqrt[{3}]{2}}i}}{\Bigg \{}{\sqrt[{3}]{\left[2(1+{\sqrt {3}}){\sqrt {5+{\sqrt {5}}}}+{\sqrt {2}}({\sqrt {5}}-1)({\sqrt {3}}-1)\right]+i\left[2(1-{\sqrt {3}}){\sqrt {5+{\sqrt {5}}}}+{\sqrt {2}}({\sqrt {5}}-1)({\sqrt {3}}+1)\right]}}}
−
[
2
(
1
+
3
)
5
+
5
+
2
(
5
−
1
)
(
3
−
1
)
]
−
i
[
2
(
1
−
3
)
5
+
5
+
2
(
5
−
1
)
(
3
+
1
)
]
3
}
{\displaystyle -{\sqrt[{3}]{\left[2(1+{\sqrt {3}}){\sqrt {5+{\sqrt {5}}}}+{\sqrt {2}}({\sqrt {5}}-1)({\sqrt {3}}-1)\right]-i\left[2(1-{\sqrt {3}}){\sqrt {5+{\sqrt {5}}}}+{\sqrt {2}}({\sqrt {5}}-1)({\sqrt {3}}+1)\right]}}{\Bigg \}}}
[ 1]
例如:21° = 9° + 12°
sin
(
x
±
y
)
=
sin
(
x
)
cos
(
y
)
±
cos
(
x
)
sin
(
y
)
{\displaystyle \sin(x\pm y)=\sin(x)\cos(y)\pm \cos(x)\sin(y)\,}
cos
(
x
±
y
)
=
cos
(
x
)
cos
(
y
)
∓
sin
(
x
)
sin
(
y
)
{\displaystyle \cos(x\pm y)=\cos(x)\cos(y)\mp \sin(x)\sin(y)\,}
Chord(36°) = a/b = 1/f, from 托勒密定理 例如:18°
c
r
d
36
∘
=
c
r
d
(
∠
A
D
B
)
=
a
b
=
2
1
+
5
{\displaystyle \mathrm {crd} \ {36^{\circ }}=\mathrm {crd} \left(\angle \mathrm {ADB} \right)={\frac {a}{b}}={\frac {2}{1+{\sqrt {5}}}}}
c
r
d
θ
=
2
sin
θ
2
{\displaystyle \mathrm {crd} \ {\theta }=2\sin {\frac {\theta }{2}}\,}
sin
18
∘
=
1
1
+
5
=
1
4
(
5
−
1
)
{\displaystyle \sin {18^{\circ }}={\frac {1}{1+{\sqrt {5}}}}={\tfrac {1}{4}}\left({\sqrt {5}}-1\right)}
由於三角函數的特性,大於45°角度的三角函數值,可以經由自0°~45°的角度的三角函數值的相關的計算取得。
sin
0
=
0
{\displaystyle \sin 0=0\,}
cos
0
=
1
{\displaystyle \cos 0=1\,}
tan
0
=
0
{\displaystyle \tan 0=0\,}
sin
1
∘
=
1
+
3
i
16
4
30
−
8
15
+
3
5
+
8
5
+
5
+
4
10
−
4
6
−
4
2
+
(
4
30
+
8
15
+
3
5
+
8
5
+
5
−
4
10
−
4
6
+
4
2
)
i
3
+
{\displaystyle \sin {1^{\circ }}={\frac {1+{\sqrt {3}}i}{16}}{\sqrt[{3}]{4{\sqrt {30}}-8{\sqrt {15+3{\sqrt {5}}}}+8{\sqrt {5+{\sqrt {5}}}}+4{\sqrt {10}}-4{\sqrt {6}}-4{\sqrt {2}}+\left(4{\sqrt {30}}+8{\sqrt {15+3{\sqrt {5}}}}+8{\sqrt {5+{\sqrt {5}}}}-4{\sqrt {10}}-4{\sqrt {6}}+4{\sqrt {2}}\right)i}}+}
1
−
3
i
16
4
30
−
8
15
+
3
5
+
8
5
+
5
+
4
10
−
4
6
−
4
2
−
(
4
30
+
8
15
+
3
5
+
8
5
+
5
−
4
10
−
4
6
+
4
2
)
i
3
{\displaystyle {\frac {1-{\sqrt {3}}i}{16}}{\sqrt[{3}]{4{\sqrt {30}}-8{\sqrt {15+3{\sqrt {5}}}}+8{\sqrt {5+{\sqrt {5}}}}+4{\sqrt {10}}-4{\sqrt {6}}-4{\sqrt {2}}-\left(4{\sqrt {30}}+8{\sqrt {15+3{\sqrt {5}}}}+8{\sqrt {5+{\sqrt {5}}}}-4{\sqrt {10}}-4{\sqrt {6}}+4{\sqrt {2}}\right)i}}}
[ 2]
sin
2
∘
=
1
2
i
(
cos
6
∘
+
i
sin
6
∘
3
−
cos
6
∘
−
i
sin
6
∘
3
)
{\displaystyle \sin {2^{\circ }}={\frac {1}{2i}}\left({\sqrt[{3}]{\cos {6^{\circ }}+i\sin {6^{\circ }}}}-{\sqrt[{3}]{\cos {6^{\circ }}-i\sin {6^{\circ }}}}\right)}
=
1
4
i
{
[
2
(
5
−
5
)
+
3
(
5
+
1
)
]
+
i
[
6
(
5
−
5
)
−
5
−
1
]
3
{\displaystyle ={\frac {1}{4i}}{\Bigg \{}{\sqrt[{3}]{\left[{\sqrt {2(5-{\sqrt {5}})}}+{\sqrt {3}}({\sqrt {5}}+1)\right]+i\left[{\sqrt {6(5-{\sqrt {5}})}}-{\sqrt {5}}-1\right]}}}
−
[
2
(
5
−
5
)
+
3
(
5
+
1
)
]
−
i
[
6
(
5
−
5
)
−
5
−
1
]
3
}
{\displaystyle -{\sqrt[{3}]{\left[{\sqrt {2(5-{\sqrt {5}})}}+{\sqrt {3}}({\sqrt {5}}+1)\right]-i\left[{\sqrt {6(5-{\sqrt {5}})}}-{\sqrt {5}}-1\right]}}{\Bigg \}}}
cos
2
∘
=
1
2
(
cos
6
∘
+
i
sin
6
∘
3
+
cos
6
∘
−
i
sin
6
∘
3
)
{\displaystyle \cos {2^{\circ }}={\frac {1}{2}}\left({\sqrt[{3}]{\cos {6^{\circ }}+i\sin {6^{\circ }}}}+{\sqrt[{3}]{\cos {6^{\circ }}-i\sin {6^{\circ }}}}\right)}
=
1
4
{
[
2
(
5
−
5
)
+
3
(
5
+
1
)
]
+
i
[
6
(
5
−
5
)
−
5
−
1
]
3
{\displaystyle ={\frac {1}{4}}{\Bigg \{}{\sqrt[{3}]{\left[{\sqrt {2(5-{\sqrt {5}})}}+{\sqrt {3}}({\sqrt {5}}+1)\right]+i\left[{\sqrt {6(5-{\sqrt {5}})}}-{\sqrt {5}}-1\right]}}}
+
[
2
(
5
−
5
)
+
3
(
5
+
1
)
]
−
i
[
6
(
5
−
5
)
−
5
−
1
]
3
}
{\displaystyle +{\sqrt[{3}]{\left[{\sqrt {2(5-{\sqrt {5}})}}+{\sqrt {3}}({\sqrt {5}}+1)\right]-i\left[{\sqrt {6(5-{\sqrt {5}})}}-{\sqrt {5}}-1\right]}}{\Bigg \}}}
sin
π
60
=
sin
3
∘
=
1
4
8
−
3
−
15
−
10
−
2
5
{\displaystyle \sin {\frac {\pi }{60}}=\sin 3^{\circ }={\tfrac {1}{4}}{\sqrt {8-{\sqrt {3}}-{\sqrt {15}}-{\sqrt {10-2{\sqrt {5}}}}}}\,}
cos
π
60
=
cos
3
∘
=
1
4
8
+
3
+
15
+
10
−
2
5
{\displaystyle \cos {\frac {\pi }{60}}=\cos 3^{\circ }={\tfrac {1}{4}}{\sqrt {8+{\sqrt {3}}+{\sqrt {15}}+{\sqrt {10-2{\sqrt {5}}}}}}\,}
tan
π
60
=
tan
3
∘
=
1
4
[
(
2
−
3
)
(
3
+
5
)
−
2
]
[
2
−
2
(
5
−
5
)
]
{\displaystyle \tan {\frac {\pi }{60}}=\tan 3^{\circ }={\tfrac {1}{4}}\left[(2-{\sqrt {3}})(3+{\sqrt {5}})-2\right]\left[2-{\sqrt {2(5-{\sqrt {5}})}}\right]\,}
sin
4
∘
=
1
2
i
(
cos
12
∘
+
i
sin
12
∘
3
−
cos
12
∘
−
i
sin
12
∘
3
)
{\displaystyle \sin {4^{\circ }}={\frac {1}{2i}}\left({\sqrt[{3}]{\cos {12^{\circ }}+i\sin {12^{\circ }}}}-{\sqrt[{3}]{\cos {12^{\circ }}-i\sin {12^{\circ }}}}\right)}
=
1
4
i
{
[
6
(
5
+
5
)
+
5
−
1
]
+
i
[
2
(
5
+
5
)
−
3
(
5
−
1
)
]
3
{\displaystyle ={\frac {1}{4i}}{\Bigg \{}{\sqrt[{3}]{\left[{\sqrt {6(5+{\sqrt {5}})}}+{\sqrt {5}}-1\right]+i\left[{\sqrt {2(5+{\sqrt {5}})}}-{\sqrt {3}}({\sqrt {5}}-1)\right]}}}
−
[
6
(
5
+
5
)
+
5
−
1
]
−
i
[
2
(
5
+
5
)
−
3
(
5
−
1
)
]
3
}
{\displaystyle -{\sqrt[{3}]{\left[{\sqrt {6(5+{\sqrt {5}})}}+{\sqrt {5}}-1\right]-i\left[{\sqrt {2(5+{\sqrt {5}})}}-{\sqrt {3}}({\sqrt {5}}-1)\right]}}{\Bigg \}}}
cos
4
∘
=
1
2
(
cos
12
∘
+
i
sin
12
∘
3
+
cos
12
∘
−
i
sin
12
∘
3
)
{\displaystyle \cos {4^{\circ }}={\frac {1}{2}}\left({\sqrt[{3}]{\cos {12^{\circ }}+i\sin {12^{\circ }}}}+{\sqrt[{3}]{\cos {12^{\circ }}-i\sin {12^{\circ }}}}\right)}
=
1
4
{
[
6
(
5
+
5
)
+
5
−
1
]
+
i
[
2
(
5
+
5
)
−
3
(
5
−
1
)
]
3
{\displaystyle ={\frac {1}{4}}{\Bigg \{}{\sqrt[{3}]{\left[{\sqrt {6(5+{\sqrt {5}})}}+{\sqrt {5}}-1\right]+i\left[{\sqrt {2(5+{\sqrt {5}})}}-{\sqrt {3}}({\sqrt {5}}-1)\right]}}}
+
[
6
(
5
+
5
)
+
5
−
1
]
−
i
[
2
(
5
+
5
)
−
3
(
5
−
1
)
]
3
}
{\displaystyle +{\sqrt[{3}]{\left[{\sqrt {6(5+{\sqrt {5}})}}+{\sqrt {5}}-1\right]-i\left[{\sqrt {2(5+{\sqrt {5}})}}-{\sqrt {3}}({\sqrt {5}}-1)\right]}}{\Bigg \}}}
sin
π
36
=
sin
5
∘
=
2
−
2
3
i
2
2
(
2
−
6
)
3
−
2
−
3
−
(
1
+
3
i
)
2
(
2
−
6
)
3
−
2
−
3
8
{\displaystyle \sin {\frac {\pi }{36}}=\sin 5^{\circ }={\frac {2-2{\sqrt {3}}\mathrm {i} }{2{\sqrt[{3}]{2({\sqrt {2}}-{\sqrt {6}})}}-2-{\sqrt {3}}}}-{\frac {(1+{\sqrt {3}}\mathrm {i} ){\sqrt[{3}]{2({\sqrt {2}}-{\sqrt {6}})}}-2-{\sqrt {3}}}{8}}\,}
sin
π
30
=
sin
6
∘
=
1
8
[
6
(
5
−
5
)
−
5
−
1
]
{\displaystyle \sin {\frac {\pi }{30}}=\sin 6^{\circ }={\tfrac {1}{8}}\left[{\sqrt {6(5-{\sqrt {5}})}}-{\sqrt {5}}-1\right]\,}
cos
π
30
=
cos
6
∘
=
1
8
[
2
(
5
−
5
)
+
3
(
5
+
1
)
]
{\displaystyle \cos {\frac {\pi }{30}}=\cos 6^{\circ }={\tfrac {1}{8}}\left[{\sqrt {2(5-{\sqrt {5}})}}+{\sqrt {3}}({\sqrt {5}}+1)\right]\,}
tan
π
30
=
tan
6
∘
=
1
2
[
2
(
5
−
5
)
−
3
(
5
−
1
)
]
{\displaystyle \tan {\frac {\pi }{30}}=\tan 6^{\circ }={\tfrac {1}{2}}\left[{\sqrt {2(5-{\sqrt {5}})}}-{\sqrt {3}}({\sqrt {5}}-1)\right]\,}
cot
π
30
=
cot
6
∘
=
1
2
(
50
+
22
5
+
3
3
+
15
)
{\displaystyle \cot {\frac {\pi }{30}}=\cot 6^{\circ }={\tfrac {1}{2}}\left({\sqrt {50+22{\sqrt {5}}}}+3{\sqrt {3}}+{\sqrt {15}}\right)\,}
sec
π
30
=
sec
6
∘
=
3
−
5
−
2
5
{\displaystyle \sec {\frac {\pi }{30}}=\sec 6^{\circ }={\sqrt {3}}-{\sqrt {5-2{\sqrt {5}}}}\,}
csc
π
30
=
csc
6
∘
=
2
+
5
+
15
+
6
5
{\displaystyle \csc {\frac {\pi }{30}}=\csc 6^{\circ }=2+{\sqrt {5}}+{\sqrt {15+6{\sqrt {5}}}}\,}
sin
π
24
=
sin
7.5
∘
=
1
4
8
−
2
6
−
2
2
{\displaystyle \sin {\frac {\pi }{24}}=\sin 7.5^{\circ }={\tfrac {1}{4}}{\sqrt {8-2{\sqrt {6}}-2{\sqrt {2}}}}\,}
cos
π
24
=
cos
7.5
∘
=
1
4
8
+
2
6
+
2
2
{\displaystyle \cos {\frac {\pi }{24}}=\cos 7.5^{\circ }={\tfrac {1}{4}}{\sqrt {8+2{\sqrt {6}}+2{\sqrt {2}}}}\,}
tan
π
24
=
tan
7.5
∘
=
6
+
2
−
2
−
3
{\displaystyle \tan {\frac {\pi }{24}}=\tan 7.5^{\circ }={\sqrt {6}}+{\sqrt {2}}-2-{\sqrt {3}}\,}
cot
π
24
=
cot
7.5
∘
=
6
+
2
+
2
+
3
{\displaystyle \cot {\frac {\pi }{24}}=\cot 7.5^{\circ }={\sqrt {6}}+{\sqrt {2}}+2+{\sqrt {3}}\,}
sec
π
24
=
sec
7.5
∘
=
16
−
6
6
−
10
2
+
8
3
{\displaystyle \sec {\frac {\pi }{24}}=\sec 7.5^{\circ }={\sqrt {16-6{\sqrt {6}}-10{\sqrt {2}}+8{\sqrt {3}}}}\,}
csc
π
24
=
csc
7.5
∘
=
16
+
6
6
+
10
2
+
8
3
{\displaystyle \csc {\frac {\pi }{24}}=\csc 7.5^{\circ }={\sqrt {16+6{\sqrt {6}}+10{\sqrt {2}}+8{\sqrt {3}}}}\,}
sin
π
20
=
sin
9
∘
=
1
4
8
−
2
10
+
2
5
{\displaystyle \sin {\frac {\pi }{20}}=\sin 9^{\circ }={\tfrac {1}{4}}{\sqrt {8-2{\sqrt {10+2{\sqrt {5}}}}}}\,}
cos
π
20
=
cos
9
∘
=
1
4
8
+
2
10
+
2
5
{\displaystyle \cos {\frac {\pi }{20}}=\cos 9^{\circ }={\tfrac {1}{4}}{\sqrt {8+2{\sqrt {10+2{\sqrt {5}}}}}}\,}
tan
π
20
=
tan
9
∘
=
5
+
1
−
5
+
2
5
{\displaystyle \tan {\frac {\pi }{20}}=\tan 9^{\circ }={\sqrt {5}}+1-{\sqrt {5+2{\sqrt {5}}}}\,}
cot
π
20
=
cot
9
∘
=
5
+
1
+
5
+
2
5
{\displaystyle \cot {\frac {\pi }{20}}=\cot 9^{\circ }={\sqrt {5}}+1+{\sqrt {5+2{\sqrt {5}}}}\,}
tan
10
∘
=
−
−
1
−
3
i
6
−
12
3
+
36
i
3
−
−
1
+
3
i
6
−
12
3
−
36
i
3
+
1
3
{\displaystyle {\tan 10^{\circ }=-{\frac {-1-{\sqrt {3}}{\rm {i}}}{6}}{\sqrt[{3}]{-12{\sqrt {3}}+36{\rm {i}}}}-{\frac {-1+{\sqrt {3}}{\rm {i}}}{6}}{\sqrt[{3}]{-12{\sqrt {3}}-36{\rm {i}}}}+{\frac {1}{\sqrt {3}}}}\,}
sin
π
15
=
sin
12
∘
=
1
8
[
2
(
5
+
5
)
−
3
(
5
−
1
)
]
{\displaystyle \sin {\frac {\pi }{15}}=\sin 12^{\circ }={\tfrac {1}{8}}\left[{\sqrt {2(5+{\sqrt {5}})}}-{\sqrt {3}}({\sqrt {5}}-1)\right]\,}
cos
π
15
=
cos
12
∘
=
1
8
[
6
(
5
+
5
)
+
5
−
1
]
{\displaystyle \cos {\frac {\pi }{15}}=\cos 12^{\circ }={\tfrac {1}{8}}\left[{\sqrt {6(5+{\sqrt {5}})}}+{\sqrt {5}}-1\right]\,}
tan
π
15
=
tan
12
∘
=
1
2
[
3
(
3
−
5
)
−
2
(
25
−
11
5
)
]
{\displaystyle \tan {\frac {\pi }{15}}=\tan 12^{\circ }={\tfrac {1}{2}}\left[{\sqrt {3}}(3-{\sqrt {5}})-{\sqrt {2(25-11{\sqrt {5}})}}\right]\,}
sin
π
12
=
sin
15
∘
=
1
4
2
(
3
−
1
)
{\displaystyle \sin {\frac {\pi }{12}}=\sin 15^{\circ }={\tfrac {1}{4}}{\sqrt {2}}\left({\sqrt {3}}-1\right)\,}
cos
π
12
=
cos
15
∘
=
1
4
2
(
3
+
1
)
{\displaystyle \cos {\frac {\pi }{12}}=\cos 15^{\circ }={\tfrac {1}{4}}{\sqrt {2}}\left({\sqrt {3}}+1\right)\,}
tan
π
12
=
tan
15
∘
=
2
−
3
{\displaystyle \tan {\frac {\pi }{12}}=\tan 15^{\circ }=2-{\sqrt {3}}\,}
sin
π
10
=
sin
18
∘
=
1
4
(
5
−
1
)
=
1
2
φ
−
1
{\displaystyle \sin {\frac {\pi }{10}}=\sin 18^{\circ }={\tfrac {1}{4}}\left({\sqrt {5}}-1\right)={\tfrac {1}{2}}\varphi ^{-1}\,}
cos
π
10
=
cos
18
∘
=
1
4
2
(
5
+
5
)
{\displaystyle \cos {\frac {\pi }{10}}=\cos 18^{\circ }={\tfrac {1}{4}}{\sqrt {2\left(5+{\sqrt {5}}\right)}}\,}
tan
π
10
=
tan
18
∘
=
1
5
5
(
5
−
2
5
)
{\displaystyle \tan {\frac {\pi }{10}}=\tan 18^{\circ }={\tfrac {1}{5}}{\sqrt {5\left(5-2{\sqrt {5}}\right)}}\,}
sin
π
9
=
sin
20
∘
=
−
3
16
+
−
1
256
3
+
−
3
16
−
−
1
256
3
=
{\displaystyle \sin {\frac {\pi }{9}}=\sin 20^{\circ }={\sqrt[{3}]{-{\frac {\sqrt {3}}{16}}+{\sqrt {-{\frac {1}{256}}}}}}+{\sqrt[{3}]{-{\frac {\sqrt {3}}{16}}-{\sqrt {-{\frac {1}{256}}}}}}=}
2
−
4
3
(
i
−
3
3
−
i
+
3
3
)
{\displaystyle 2^{-{\frac {4}{3}}}\left({\sqrt[{3}]{i-{\sqrt {3}}}}-{\sqrt[{3}]{i+{\sqrt {3}}}}\right)}
cos
π
9
=
cos
20
∘
=
{\displaystyle \cos {\frac {\pi }{9}}=\cos 20^{\circ }=}
2
−
4
3
(
1
+
i
3
3
+
1
−
i
3
3
)
{\displaystyle 2^{-{\frac {4}{3}}}\left({\sqrt[{3}]{1+i{\sqrt {3}}}}+{\sqrt[{3}]{1-i{\sqrt {3}}}}\right)}
sin
7
π
60
=
sin
21
∘
=
1
4
8
+
3
−
15
−
10
+
2
5
{\displaystyle \sin {\frac {7\pi }{60}}=\sin 21^{\circ }={\tfrac {1}{4}}{\sqrt {8+{\sqrt {3}}-{\sqrt {15}}-{\sqrt {10+2{\sqrt {5}}}}}}\,}
cos
7
π
60
=
cos
21
∘
=
1
4
8
−
3
+
15
+
10
+
2
5
{\displaystyle \cos {\frac {7\pi }{60}}=\cos 21^{\circ }={\tfrac {1}{4}}{\sqrt {8-{\sqrt {3}}+{\sqrt {15}}+{\sqrt {10+2{\sqrt {5}}}}}}\,}
tan
7
π
60
=
tan
21
∘
=
1
4
[
2
−
(
2
+
3
)
(
3
−
5
)
]
[
2
−
2
(
5
+
5
)
]
{\displaystyle \tan {\frac {7\pi }{60}}=\tan 21^{\circ }={\tfrac {1}{4}}\left[2-\left(2+{\sqrt {3}}\right)\left(3-{\sqrt {5}}\right)\right]\left[2-{\sqrt {2\left(5+{\sqrt {5}}\right)}}\right]\,}
(
21
3
17
)
∘
{\displaystyle \mathbf {\left(21{\frac {3}{17}}\right)^{\circ }} }
(
360
17
)
∘
{\displaystyle \mathbf {\left({\frac {360}{17}}\right)^{\circ }} }
正十七邊形
cos
2
π
17
=
−
1
+
17
+
34
−
2
17
+
2
17
+
3
17
−
34
−
2
17
−
2
34
+
2
17
16
{\displaystyle \operatorname {cos} {2\pi \over 17}={\frac {-1+{\sqrt {17}}+{\sqrt {34-2{\sqrt {17}}}}+2{\sqrt {17+3{\sqrt {17}}-{\sqrt {34-2{\sqrt {17}}}}-2{\sqrt {34+2{\sqrt {17}}}}}}}{16}}}
sin
π
8
=
sin
22.5
∘
=
1
2
(
2
−
2
)
{\displaystyle \sin {\frac {\pi }{8}}=\sin 22.5^{\circ }={\tfrac {1}{2}}({\sqrt {2-{\sqrt {2}}}})}
cos
π
8
=
cos
22.5
∘
=
1
2
(
2
+
2
)
{\displaystyle \cos {\frac {\pi }{8}}=\cos 22.5^{\circ }={\tfrac {1}{2}}({\sqrt {2+{\sqrt {2}}}})\,}
tan
π
8
=
tan
22.5
∘
=
2
−
1
{\displaystyle \tan {\frac {\pi }{8}}=\tan 22.5^{\circ }={\sqrt {2}}-1\,}
sin
2
π
15
=
sin
24
∘
=
1
8
[
3
(
5
+
1
)
−
2
5
−
5
]
{\displaystyle \sin {\frac {2\pi }{15}}=\sin 24^{\circ }={\tfrac {1}{8}}\left[{\sqrt {3}}({\sqrt {5}}+1)-{\sqrt {2}}{\sqrt {5-{\sqrt {5}}}}\right]\,}
cos
2
π
15
=
cos
24
∘
=
1
8
(
6
5
−
5
+
5
+
1
)
{\displaystyle \cos {\frac {2\pi }{15}}=\cos 24^{\circ }={\tfrac {1}{8}}\left({\sqrt {6}}{\sqrt {5-{\sqrt {5}}}}+{\sqrt {5}}+1\right)\,}
tan
2
π
15
=
tan
24
∘
=
1
2
[
2
(
25
+
11
5
)
−
3
(
3
+
5
)
]
{\displaystyle \tan {\frac {2\pi }{15}}=\tan 24^{\circ }={\tfrac {1}{2}}\left[{\sqrt {2(25+11{\sqrt {5}})}}-{\sqrt {3}}(3+{\sqrt {5}})\right]\,}
(
25
5
7
)
∘
{\displaystyle \mathbf {\left(25{\frac {5}{7}}\right)^{\circ }} }
(
180
7
)
∘
{\displaystyle \mathbf {\left({\frac {180}{7}}\right)^{\circ }} }
正七邊形
cos
π
7
=
cos
180
7
∘
=
cos
25
5
7
∘
=
1
6
+
1
−
3
i
24
28
−
84
3
i
3
+
1
+
3
i
24
28
−
84
3
i
3
{\displaystyle \cos {\frac {\pi }{7}}=\cos {\frac {180}{7}}^{\circ }=\cos 25{\frac {5}{7}}^{\circ }={\frac {1}{6}}+{\frac {1-{\sqrt {3}}i}{24}}{\sqrt[{3}]{28-84{\sqrt {3}}i}}+{\frac {1+{\sqrt {3}}i}{24}}{\sqrt[{3}]{28-84{\sqrt {3}}i}}}
sin
3
π
20
=
sin
27
∘
=
1
8
[
2
5
+
5
−
2
(
5
−
1
)
]
{\displaystyle \sin {\frac {3\pi }{20}}=\sin 27^{\circ }={\tfrac {1}{8}}\left[2{\sqrt {5+{\sqrt {5}}}}-{\sqrt {2}}\;({\sqrt {5}}-1)\right]\,}
cos
3
π
20
=
cos
27
∘
=
1
8
[
2
5
+
5
+
2
(
5
−
1
)
]
{\displaystyle \cos {\frac {3\pi }{20}}=\cos 27^{\circ }={\tfrac {1}{8}}\left[2{\sqrt {5+{\sqrt {5}}}}+{\sqrt {2}}\;\left({\sqrt {5}}-1\right)\right]\,}
tan
3
π
20
=
tan
27
∘
=
5
−
1
−
5
−
2
5
{\displaystyle \tan {\frac {3\pi }{20}}=\tan 27^{\circ }={\sqrt {5}}-1-{\sqrt {5-2{\sqrt {5}}}}\,}
sin
π
6
=
sin
30
∘
=
1
2
{\displaystyle \sin {\frac {\pi }{6}}=\sin 30^{\circ }={\tfrac {1}{2}}\,}
cos
π
6
=
cos
30
∘
=
1
2
3
{\displaystyle \cos {\frac {\pi }{6}}=\cos 30^{\circ }={\tfrac {1}{2}}{\sqrt {3}}\,}
tan
π
6
=
tan
30
∘
=
1
3
3
{\displaystyle \tan {\frac {\pi }{6}}=\tan 30^{\circ }={\tfrac {1}{3}}{\sqrt {3}}\,}
sin
11
π
60
=
sin
33
∘
=
1
4
8
−
3
−
15
+
10
−
2
5
{\displaystyle \sin {\frac {11\pi }{60}}=\sin 33^{\circ }={\tfrac {1}{4}}{\sqrt {8-{\sqrt {3}}-{\sqrt {15}}+{\sqrt {10-2{\sqrt {5}}}}}}\,}
cos
11
π
60
=
cos
33
∘
=
1
4
8
+
3
+
15
−
10
−
2
5
{\displaystyle \cos {\frac {11\pi }{60}}=\cos 33^{\circ }={\tfrac {1}{4}}{\sqrt {8+{\sqrt {3}}+{\sqrt {15}}-{\sqrt {10-2{\sqrt {5}}}}}}\,}
tan
11
π
60
=
tan
33
∘
=
1
4
(
2
3
−
5
−
1
)
(
2
5
+
2
5
+
3
+
5
)
{\displaystyle \tan {\frac {11\pi }{60}}=\tan 33^{\circ }={\tfrac {1}{4}}\left(2{\sqrt {3}}-{\sqrt {5}}-1\right)\left(2{\sqrt {5+2{\sqrt {5}}}}+3+{\sqrt {5}}\right)\,}
cot
11
π
60
=
cot
33
∘
=
1
4
(
2
3
+
5
+
1
)
(
2
5
+
2
5
−
3
−
5
)
{\displaystyle \cot {\frac {11\pi }{60}}=\cot 33^{\circ }={\tfrac {1}{4}}\left(2{\sqrt {3}}+{\sqrt {5}}+1\right)\left(2{\sqrt {5+2{\sqrt {5}}}}-3-{\sqrt {5}}\right)\,}
sin
π
5
=
sin
36
∘
=
1
4
[
2
(
5
−
5
)
]
{\displaystyle \sin {\frac {\pi }{5}}=\sin 36^{\circ }={\tfrac {1}{4}}\left[{\sqrt {2\left(5-{\sqrt {5}}\right)}}\right]\,}
cos
π
5
=
cos
36
∘
=
1
+
5
4
=
1
2
φ
{\displaystyle \cos {\frac {\pi }{5}}=\cos 36^{\circ }={\frac {1+{\sqrt {5}}}{4}}={\tfrac {1}{2}}\varphi \,}
tan
π
5
=
tan
36
∘
=
5
−
2
5
{\displaystyle \tan {\frac {\pi }{5}}=\tan 36^{\circ }={\sqrt {5-2{\sqrt {5}}}}\,}
sin
13
π
60
=
sin
39
∘
=
1
4
8
−
3
+
15
+
10
+
2
5
{\displaystyle \sin {\frac {13\pi }{60}}=\sin 39^{\circ }={\tfrac {1}{4}}{\sqrt {8-{\sqrt {3}}+{\sqrt {15}}+{\sqrt {10+2{\sqrt {5}}}}}}\,}
cos
13
π
60
=
cos
39
∘
=
1
4
8
+
3
−
15
+
10
+
2
5
{\displaystyle \cos {\frac {13\pi }{60}}=\cos 39^{\circ }={\tfrac {1}{4}}{\sqrt {8+{\sqrt {3}}-{\sqrt {15}}+{\sqrt {10+2{\sqrt {5}}}}}}\,}
tan
13
π
60
=
tan
39
∘
=
1
4
[
(
2
−
3
)
(
3
−
5
)
−
2
]
[
2
−
2
(
5
+
5
)
]
{\displaystyle \tan {\frac {13\pi }{60}}=\tan 39^{\circ }={\tfrac {1}{4}}\left[\left(2-{\sqrt {3}}\right)\left(3-{\sqrt {5}}\right)-2\right]\left[2-{\sqrt {2\left(5+{\sqrt {5}}\right)}}\right]\,}
sin
7
π
30
=
sin
42
∘
=
6
5
+
5
−
5
+
1
8
{\displaystyle \sin {\frac {7\pi }{30}}=\sin 42^{\circ }={\frac {{\sqrt {6}}{\sqrt {5+{\sqrt {5}}}}-{\sqrt {5}}+1}{8}}\,}
cos
7
π
30
=
cos
42
∘
=
2
5
+
5
+
3
(
5
−
1
)
8
{\displaystyle \cos {\frac {7\pi }{30}}=\cos 42^{\circ }={\frac {{\sqrt {2}}{\sqrt {5+{\sqrt {5}}}}+{\sqrt {3}}\left({\sqrt {5}}-1\right)}{8}}\,}
tan
7
π
30
=
tan
42
∘
=
1
2
(
3
+
15
−
10
+
2
5
)
{\displaystyle \tan {\frac {7\pi }{30}}=\tan 42^{\circ }={\frac {1}{2}}\left({\sqrt {3}}+{\sqrt {15}}-{\sqrt {10+2{\sqrt {5}}}}\right)\,}
cot
7
π
30
=
cot
42
∘
=
1
2
(
3
3
−
15
+
50
−
22
5
)
{\displaystyle \cot {\frac {7\pi }{30}}=\cot 42^{\circ }={\frac {1}{2}}\left(3{\sqrt {3}}-{\sqrt {15}}+{\sqrt {50-22{\sqrt {5}}}}\right)\,}
sec
7
π
30
=
sec
42
∘
=
5
+
2
5
−
3
{\displaystyle \sec {\frac {7\pi }{30}}=\sec 42^{\circ }={\sqrt {5+2{\sqrt {5}}}}-{\sqrt {3}}\,}
sec
7
π
30
=
sec
42
∘
=
15
−
6
5
+
5
−
2
{\displaystyle \sec {\frac {7\pi }{30}}=\sec 42^{\circ }={\sqrt {15-6{\sqrt {5}}}}+{\sqrt {5}}-2\,}
sin
π
4
=
sin
45
∘
=
2
2
=
1
2
{\displaystyle \sin {\frac {\pi }{4}}=\sin 45^{\circ }={\frac {\sqrt {2}}{2}}={\frac {1}{\sqrt {2}}}\,}
cos
π
4
=
cos
45
∘
=
2
2
=
1
2
{\displaystyle \cos {\frac {\pi }{4}}=\cos 45^{\circ }={\frac {\sqrt {2}}{2}}={\frac {1}{\sqrt {2}}}\,}
tan
π
4
=
tan
45
∘
=
1
{\displaystyle \tan {\frac {\pi }{4}}=\tan 45^{\circ }=1}
n
{\displaystyle n}
sin
(
2
π
n
)
{\displaystyle \sin \left({\frac {2\pi }{n}}\right)}
cos
(
2
π
n
)
{\displaystyle \cos \left({\frac {2\pi }{n}}\right)}
tan
(
2
π
n
)
{\displaystyle \tan \left({\frac {2\pi }{n}}\right)}
1
0
{\displaystyle 0}
1
{\displaystyle 1}
0
{\displaystyle 0}
2
0
{\displaystyle 0}
−
1
{\displaystyle -1}
0
{\displaystyle 0}
3
1
2
3
{\displaystyle {\frac {1}{2}}{\sqrt {3}}}
−
1
2
{\displaystyle -{\frac {1}{2}}}
−
3
{\displaystyle -{\sqrt {3}}}
4
1
{\displaystyle 1}
0
{\displaystyle 0}
±
∞
{\displaystyle \pm \infty }
5
1
4
(
10
+
2
5
)
{\displaystyle {\frac {1}{4}}\left({\sqrt {10+2{\sqrt {5}}}}\right)}
1
4
(
5
−
1
)
{\displaystyle {\frac {1}{4}}\left({\sqrt {5}}-1\right)}
5
+
2
5
{\displaystyle {\sqrt {5+2{\sqrt {5}}}}}
6
1
2
3
{\displaystyle {\frac {1}{2}}{\sqrt {3}}}
1
2
{\displaystyle {\frac {1}{2}}}
3
{\displaystyle {\sqrt {3}}}
7
1
2
1
3
(
7
−
ω
2
7
+
21
−
3
2
3
−
ω
7
−
21
−
3
2
3
)
{\displaystyle {\frac {1}{2}}{\sqrt {{\frac {1}{3}}\left(7-\omega ^{2}{\sqrt[{3}]{\frac {7+21{\sqrt {-3}}}{2}}}-\omega {\sqrt[{3}]{\frac {7-21{\sqrt {-3}}}{2}}}\right)}}}
1
6
(
−
1
+
7
+
21
−
3
2
3
+
7
−
21
−
3
2
3
)
{\displaystyle {\frac {1}{6}}\left(-1+{\sqrt[{3}]{\frac {7+21{\sqrt {-3}}}{2}}}+{\sqrt[{3}]{\frac {7-21{\sqrt {-3}}}{2}}}\right)}
8
1
2
2
{\displaystyle {\frac {1}{2}}{\sqrt {2}}}
1
2
2
{\displaystyle {\frac {1}{2}}{\sqrt {2}}}
1
{\displaystyle 1}
9
10
1
4
(
10
−
2
5
)
{\displaystyle {\frac {1}{4}}\left({\sqrt {10-2{\sqrt {5}}}}\right)}
1
4
(
5
+
1
)
{\displaystyle {\frac {1}{4}}\left({\sqrt {5}}+1\right)}
5
−
2
5
{\displaystyle {\sqrt {5-2{\sqrt {5}}}}}
11
12
1
2
{\displaystyle {\frac {1}{2}}}
1
2
3
{\displaystyle {\frac {1}{2}}{\sqrt {3}}}
1
3
3
{\displaystyle {\frac {1}{3}}{\sqrt {3}}}
13
14
15
1
8
(
15
+
3
−
10
−
2
5
)
{\displaystyle {\frac {1}{8}}\left({\sqrt {15}}+{\sqrt {3}}-{\sqrt {10-2{\sqrt {5}}}}\right)}
1
8
(
1
+
5
+
30
−
6
5
)
{\displaystyle {\frac {1}{8}}\left(1+{\sqrt {5}}+{\sqrt {30-6{\sqrt {5}}}}\right)}
1
2
(
−
3
3
−
s
q
r
t
15
+
50
+
22
5
)
{\displaystyle {\frac {1}{2}}\left(-3{\sqrt {3}}-sqrt{15}+{\sqrt {50+22{\sqrt {5}}}}\right)}
16
1
2
(
2
−
2
)
{\displaystyle {\frac {1}{2}}\left({\sqrt {2-{\sqrt {2}}}}\right)}
1
2
(
2
+
2
)
{\displaystyle {\frac {1}{2}}\left({\sqrt {2+{\sqrt {2}}}}\right)}
2
−
1
{\displaystyle {\sqrt {2}}-1}
17
1
16
(
−
1
+
17
+
34
−
2
17
+
2
17
+
3
17
−
34
−
2
17
−
2
34
+
2
17
)
{\displaystyle {\frac {1}{16}}\left(-1+{\sqrt {17}}+{\sqrt {34-2{\sqrt {17}}}}+2{\sqrt {17+3{\sqrt {17}}-{\sqrt {34-2{\sqrt {17}}}}-2{\sqrt {34+2{\sqrt {17}}}}}}\right)}
18
1
4
(
4
i
−
4
3
3
−
4
i
+
4
3
3
)
{\displaystyle {\frac {1}{4}}\left({\sqrt[{3}]{4i-4{\sqrt {3}}}}-{\sqrt[{3}]{4i+4{\sqrt {3}}}}\right)}
1
4
(
4
+
4
i
3
3
+
4
−
4
i
3
3
)
{\displaystyle {\frac {1}{4}}\left({\sqrt[{3}]{4+4i{\sqrt {3}}}}+{\sqrt[{3}]{4-4i{\sqrt {3}}}}\right)}
19
20
1
4
(
5
−
1
)
{\displaystyle {\frac {1}{4}}\left({\sqrt {5}}-1\right)}
1
4
(
10
+
2
5
)
{\displaystyle {\frac {1}{4}}\left({\sqrt {10+2{\sqrt {5}}}}\right)}
1
5
(
25
−
10
5
)
{\displaystyle {\frac {1}{5}}\left({\sqrt {25-10{\sqrt {5}}}}\right)}
21
22
23
24
1
2
(
6
−
2
)
{\displaystyle {\frac {1}{2}}\left({\sqrt {6}}-{\sqrt {2}}\right)}
1
2
(
6
+
2
)
{\displaystyle {\frac {1}{2}}\left({\sqrt {6}}+{\sqrt {2}}\right)}
2
−
3
{\displaystyle 2-{\sqrt {3}}}
埃里克·韦斯坦因 . Constructible polygon . MathWorld . 埃里克·韦斯坦因 . Trigonometry angles . MathWorld . Bracken, Paul; Cizek, Jiri. Evaluation of quantum mechanical perturbation sums in terms of quadratic surds and their use in approximation of zeta(3)/pi^3. Int. J. Quantum Chemistry. 2002, 90 (1): 42–53. doi:10.1002/qua.1803 Conway, John H.; Radin, Charles; Radun, Lorenzo. On angles whose squared trigonometric functions are rational. 1998. arXiv:math-ph/9812019 Conway, John H.; Radin, Charles; Radun, Lorenzo. On angles whose squared trigonometric functions are rational. Disc. Comput. Geom. 1999, 22 (3): 321–332. doi:10.1007/PL00009463 MR 1706614 Girstmair, Kurt. Some linear relations between values of trigonometric functions at k*pi/n. Acta Arithmetica. 1997, 81 : 387–398. MR 1472818 Gurak, S. On the minimal polynomial of gauss periods for prime powers. Mathematics of Computation. 2006, 75 (256): 2021–2035. Bibcode:2006MaCom..75.2021G doi:10.1090/S0025-5718-06-01885-0 MR 2240647 Servi, L. D. Nested square roots of 2. Am. Math. Monthly. 2003, 110 (4): 326–330. doi:10.2307/3647881 MR 1984573
^ 由Wolfram Alpha 验算:[1]
^ 使用Mathematica驗算,代碼為N[ArcSin[(1 + Sqrt[3] I)/16 Power[4 Sqrt[30] - 8 Sqrt[15 + 3 Sqrt[5]] + 8 Sqrt[5 + Sqrt[5]] + 4 Sqrt[10] - 4 Sqrt[6] - 4 Sqrt[2] + (4 Sqrt[30] + 8 Sqrt[15 + 3 Sqrt[5]] + 8 Sqrt[5 + Sqrt[5]] - 4 Sqrt[10] - 4 Sqrt[6] + 4 Sqrt[2]) I, (3)^-1] + (1 - Sqrt[3] I)/16 Power[4 Sqrt[30] - 8 Sqrt[15 + 3 Sqrt[5]] + 8 Sqrt[5 + Sqrt[5]] + 4 Sqrt[10] - 4 Sqrt[6] - 4 Sqrt[2] - (4 Sqrt[30] + 8 Sqrt[15 + 3 Sqrt[5]] + 8 Sqrt[5 + Sqrt[5]] - 4 Sqrt[10] - 4 Sqrt[6] + 4 Sqrt[2]) I, (3)^-1]], 100]/Degree結果為1與原角度無誤差


 .
.
































![{\displaystyle \sin {\frac {\pi }{9}}=\sin 20^{\circ }={\sqrt[{3}]{-{\frac {\sqrt {3}}{16}}+{\sqrt {-{\frac {1}{256}}}}}}+{\sqrt[{3}]{-{\frac {\sqrt {3}}{16}}-{\sqrt {-{\frac {1}{256}}}}}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/6019908a9d7a84324bc27625b5e5213830d24d8a)
![{\displaystyle \cos {\frac {\theta }{n}}=\Re \left({\sqrt[{n}]{\cos \theta +i\sin \theta }}\right)={\frac {1}{2}}\left({\sqrt[{n}]{\cos \theta +i\sin \theta }}+{\sqrt[{n}]{\cos \theta -i\sin \theta }}\right)}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/71c3d32e31b02c92e787505c9eafa8fa4e8cd828)
![{\displaystyle \sin {\frac {\theta }{n}}=\Im \left({\sqrt[{n}]{\cos \theta +i\sin \theta }}\right)={\frac {1}{2i}}\left({\sqrt[{n}]{\cos \theta +i\sin \theta }}-{\sqrt[{n}]{\cos \theta -i\sin \theta }}\right)}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/2ea663e7086395418f2d54876843352a2d0bf147)
![{\displaystyle \sin {1^{\circ }}={\frac {1}{2i}}\left({\sqrt[{3}]{\cos {3^{\circ }}+i\sin {3^{\circ }}}}-{\sqrt[{3}]{\cos {3^{\circ }}-i\sin {3^{\circ }}}}\right)}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/1c521d6e55fec7801936d21449aaaeb321b28e58)
![{\displaystyle ={\frac {1}{4{\sqrt[{3}]{2}}i}}{\Bigg \{}{\sqrt[{3}]{\left[2(1+{\sqrt {3}}){\sqrt {5+{\sqrt {5}}}}+{\sqrt {2}}({\sqrt {5}}-1)({\sqrt {3}}-1)\right]+i\left[2(1-{\sqrt {3}}){\sqrt {5+{\sqrt {5}}}}+{\sqrt {2}}({\sqrt {5}}-1)({\sqrt {3}}+1)\right]}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/2b16a535e1158d40e820a6c9cce5ca093eca02fe)
![{\displaystyle -{\sqrt[{3}]{\left[2(1+{\sqrt {3}}){\sqrt {5+{\sqrt {5}}}}+{\sqrt {2}}({\sqrt {5}}-1)({\sqrt {3}}-1)\right]-i\left[2(1-{\sqrt {3}}){\sqrt {5+{\sqrt {5}}}}+{\sqrt {2}}({\sqrt {5}}-1)({\sqrt {3}}+1)\right]}}{\Bigg \}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/066614d2502295fa13145c41b345358bf2238739)








![{\displaystyle \sin {1^{\circ }}={\frac {1+{\sqrt {3}}i}{16}}{\sqrt[{3}]{4{\sqrt {30}}-8{\sqrt {15+3{\sqrt {5}}}}+8{\sqrt {5+{\sqrt {5}}}}+4{\sqrt {10}}-4{\sqrt {6}}-4{\sqrt {2}}+\left(4{\sqrt {30}}+8{\sqrt {15+3{\sqrt {5}}}}+8{\sqrt {5+{\sqrt {5}}}}-4{\sqrt {10}}-4{\sqrt {6}}+4{\sqrt {2}}\right)i}}+}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/b9a7f8cda0d69d750a416bca1207841bab26cd6f)
![{\displaystyle {\frac {1-{\sqrt {3}}i}{16}}{\sqrt[{3}]{4{\sqrt {30}}-8{\sqrt {15+3{\sqrt {5}}}}+8{\sqrt {5+{\sqrt {5}}}}+4{\sqrt {10}}-4{\sqrt {6}}-4{\sqrt {2}}-\left(4{\sqrt {30}}+8{\sqrt {15+3{\sqrt {5}}}}+8{\sqrt {5+{\sqrt {5}}}}-4{\sqrt {10}}-4{\sqrt {6}}+4{\sqrt {2}}\right)i}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/36c528db784d06bd39b38158572c4ae931517615)
![{\displaystyle \sin {2^{\circ }}={\frac {1}{2i}}\left({\sqrt[{3}]{\cos {6^{\circ }}+i\sin {6^{\circ }}}}-{\sqrt[{3}]{\cos {6^{\circ }}-i\sin {6^{\circ }}}}\right)}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/9cb6011d35cbc8d89b146f7fa0a014321c9f1d09)
![{\displaystyle ={\frac {1}{4i}}{\Bigg \{}{\sqrt[{3}]{\left[{\sqrt {2(5-{\sqrt {5}})}}+{\sqrt {3}}({\sqrt {5}}+1)\right]+i\left[{\sqrt {6(5-{\sqrt {5}})}}-{\sqrt {5}}-1\right]}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/76088f823ff50097d119f0df28cff18ea03e6c6e)
![{\displaystyle -{\sqrt[{3}]{\left[{\sqrt {2(5-{\sqrt {5}})}}+{\sqrt {3}}({\sqrt {5}}+1)\right]-i\left[{\sqrt {6(5-{\sqrt {5}})}}-{\sqrt {5}}-1\right]}}{\Bigg \}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/bc8b004b90010622da546669426b9a57564c5903)
![{\displaystyle \cos {2^{\circ }}={\frac {1}{2}}\left({\sqrt[{3}]{\cos {6^{\circ }}+i\sin {6^{\circ }}}}+{\sqrt[{3}]{\cos {6^{\circ }}-i\sin {6^{\circ }}}}\right)}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/6e40bf7865e0a5ceef13869ffa29c74560bced35)
![{\displaystyle ={\frac {1}{4}}{\Bigg \{}{\sqrt[{3}]{\left[{\sqrt {2(5-{\sqrt {5}})}}+{\sqrt {3}}({\sqrt {5}}+1)\right]+i\left[{\sqrt {6(5-{\sqrt {5}})}}-{\sqrt {5}}-1\right]}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/0ed4dc0c22095244d2f44b1a13799f3d249ebca5)
![{\displaystyle +{\sqrt[{3}]{\left[{\sqrt {2(5-{\sqrt {5}})}}+{\sqrt {3}}({\sqrt {5}}+1)\right]-i\left[{\sqrt {6(5-{\sqrt {5}})}}-{\sqrt {5}}-1\right]}}{\Bigg \}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/57b380930ccaf8f99838d8352bcfc963be7680bd)


![{\displaystyle \tan {\frac {\pi }{60}}=\tan 3^{\circ }={\tfrac {1}{4}}\left[(2-{\sqrt {3}})(3+{\sqrt {5}})-2\right]\left[2-{\sqrt {2(5-{\sqrt {5}})}}\right]\,}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/9afc8cae3b0181ce3ca0fa38cd9737a9096fc5de)
![{\displaystyle \sin {4^{\circ }}={\frac {1}{2i}}\left({\sqrt[{3}]{\cos {12^{\circ }}+i\sin {12^{\circ }}}}-{\sqrt[{3}]{\cos {12^{\circ }}-i\sin {12^{\circ }}}}\right)}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/622ba2d2d653fa9a61ba26ef726e4a46cc2acafb)
![{\displaystyle ={\frac {1}{4i}}{\Bigg \{}{\sqrt[{3}]{\left[{\sqrt {6(5+{\sqrt {5}})}}+{\sqrt {5}}-1\right]+i\left[{\sqrt {2(5+{\sqrt {5}})}}-{\sqrt {3}}({\sqrt {5}}-1)\right]}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/896906922b19b21a780a055f38801474ecafd495)
![{\displaystyle -{\sqrt[{3}]{\left[{\sqrt {6(5+{\sqrt {5}})}}+{\sqrt {5}}-1\right]-i\left[{\sqrt {2(5+{\sqrt {5}})}}-{\sqrt {3}}({\sqrt {5}}-1)\right]}}{\Bigg \}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/e2d8e586d6453abd5ac515018fcbfd022fa81011)
![{\displaystyle \cos {4^{\circ }}={\frac {1}{2}}\left({\sqrt[{3}]{\cos {12^{\circ }}+i\sin {12^{\circ }}}}+{\sqrt[{3}]{\cos {12^{\circ }}-i\sin {12^{\circ }}}}\right)}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/2100bbeb5c6a431e34e47bf0f26e4c67bddd1cbb)
![{\displaystyle ={\frac {1}{4}}{\Bigg \{}{\sqrt[{3}]{\left[{\sqrt {6(5+{\sqrt {5}})}}+{\sqrt {5}}-1\right]+i\left[{\sqrt {2(5+{\sqrt {5}})}}-{\sqrt {3}}({\sqrt {5}}-1)\right]}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/d98084504214bdee5478f5af195113cb7476e2db)
![{\displaystyle +{\sqrt[{3}]{\left[{\sqrt {6(5+{\sqrt {5}})}}+{\sqrt {5}}-1\right]-i\left[{\sqrt {2(5+{\sqrt {5}})}}-{\sqrt {3}}({\sqrt {5}}-1)\right]}}{\Bigg \}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/cbd37da55c50e7c12ca7ba6ebd337630973cf60c)
![{\displaystyle \sin {\frac {\pi }{36}}=\sin 5^{\circ }={\frac {2-2{\sqrt {3}}\mathrm {i} }{2{\sqrt[{3}]{2({\sqrt {2}}-{\sqrt {6}})}}-2-{\sqrt {3}}}}-{\frac {(1+{\sqrt {3}}\mathrm {i} ){\sqrt[{3}]{2({\sqrt {2}}-{\sqrt {6}})}}-2-{\sqrt {3}}}{8}}\,}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/74aa3cf4e94e893298f0dd9edba498d11b4a2249)
![{\displaystyle \sin {\frac {\pi }{30}}=\sin 6^{\circ }={\tfrac {1}{8}}\left[{\sqrt {6(5-{\sqrt {5}})}}-{\sqrt {5}}-1\right]\,}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/e32eed64add3521d7d7c9bf695482e8c3add4c36)
![{\displaystyle \cos {\frac {\pi }{30}}=\cos 6^{\circ }={\tfrac {1}{8}}\left[{\sqrt {2(5-{\sqrt {5}})}}+{\sqrt {3}}({\sqrt {5}}+1)\right]\,}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/f90aff5eb92b8553f8dfd11cd76f3f30bd223560)
![{\displaystyle \tan {\frac {\pi }{30}}=\tan 6^{\circ }={\tfrac {1}{2}}\left[{\sqrt {2(5-{\sqrt {5}})}}-{\sqrt {3}}({\sqrt {5}}-1)\right]\,}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/ca95e17f7bfec511a0d9029c1aa1a0c8e5cc5630)













![{\displaystyle {\tan 10^{\circ }=-{\frac {-1-{\sqrt {3}}{\rm {i}}}{6}}{\sqrt[{3}]{-12{\sqrt {3}}+36{\rm {i}}}}-{\frac {-1+{\sqrt {3}}{\rm {i}}}{6}}{\sqrt[{3}]{-12{\sqrt {3}}-36{\rm {i}}}}+{\frac {1}{\sqrt {3}}}}\,}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/bff3bab5cf2730334855083f4576b03c09c9dd07)
![{\displaystyle \sin {\frac {\pi }{15}}=\sin 12^{\circ }={\tfrac {1}{8}}\left[{\sqrt {2(5+{\sqrt {5}})}}-{\sqrt {3}}({\sqrt {5}}-1)\right]\,}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/55fb1a72c84d5dec8bf231d619c534df13c261ef)
![{\displaystyle \cos {\frac {\pi }{15}}=\cos 12^{\circ }={\tfrac {1}{8}}\left[{\sqrt {6(5+{\sqrt {5}})}}+{\sqrt {5}}-1\right]\,}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/4923130317e1553f2cfd21ca42c4e29cd2f1f836)
![{\displaystyle \tan {\frac {\pi }{15}}=\tan 12^{\circ }={\tfrac {1}{2}}\left[{\sqrt {3}}(3-{\sqrt {5}})-{\sqrt {2(25-11{\sqrt {5}})}}\right]\,}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/a207e48f104ece1821014496f7b32e371956076d)






![{\displaystyle \sin {\frac {\pi }{9}}=\sin 20^{\circ }={\sqrt[{3}]{-{\frac {\sqrt {3}}{16}}+{\sqrt {-{\frac {1}{256}}}}}}+{\sqrt[{3}]{-{\frac {\sqrt {3}}{16}}-{\sqrt {-{\frac {1}{256}}}}}}=}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/1e39576a98052e848f2f9291c5d5da2437d6d056)
![{\displaystyle 2^{-{\frac {4}{3}}}\left({\sqrt[{3}]{i-{\sqrt {3}}}}-{\sqrt[{3}]{i+{\sqrt {3}}}}\right)}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/4fb7a6cadc9f67c9fc96b0b6bb7165af68824e9d)

![{\displaystyle 2^{-{\frac {4}{3}}}\left({\sqrt[{3}]{1+i{\sqrt {3}}}}+{\sqrt[{3}]{1-i{\sqrt {3}}}}\right)}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/c1fd794ae0ddf0128bdcedcca67ead75c8174e89)


![{\displaystyle \tan {\frac {7\pi }{60}}=\tan 21^{\circ }={\tfrac {1}{4}}\left[2-\left(2+{\sqrt {3}}\right)\left(3-{\sqrt {5}}\right)\right]\left[2-{\sqrt {2\left(5+{\sqrt {5}}\right)}}\right]\,}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/92f16397799bd47711ac25e404f6de198c9bb28c)






![{\displaystyle \sin {\frac {2\pi }{15}}=\sin 24^{\circ }={\tfrac {1}{8}}\left[{\sqrt {3}}({\sqrt {5}}+1)-{\sqrt {2}}{\sqrt {5-{\sqrt {5}}}}\right]\,}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/748d70aaab6ed6e9d613d6ef799e612174f96970)

![{\displaystyle \tan {\frac {2\pi }{15}}=\tan 24^{\circ }={\tfrac {1}{2}}\left[{\sqrt {2(25+11{\sqrt {5}})}}-{\sqrt {3}}(3+{\sqrt {5}})\right]\,}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/751f49b7e0a84e36750d6df47e69f7e5ca2f4ba2)


![{\displaystyle \cos {\frac {\pi }{7}}=\cos {\frac {180}{7}}^{\circ }=\cos 25{\frac {5}{7}}^{\circ }={\frac {1}{6}}+{\frac {1-{\sqrt {3}}i}{24}}{\sqrt[{3}]{28-84{\sqrt {3}}i}}+{\frac {1+{\sqrt {3}}i}{24}}{\sqrt[{3}]{28-84{\sqrt {3}}i}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/9e6f0da045735bbe37ae69faa6cb417ce734400d)
![{\displaystyle \sin {\frac {3\pi }{20}}=\sin 27^{\circ }={\tfrac {1}{8}}\left[2{\sqrt {5+{\sqrt {5}}}}-{\sqrt {2}}\;({\sqrt {5}}-1)\right]\,}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/56f979b3d0d06f3124dd266ee7860dd955e654c1)
![{\displaystyle \cos {\frac {3\pi }{20}}=\cos 27^{\circ }={\tfrac {1}{8}}\left[2{\sqrt {5+{\sqrt {5}}}}+{\sqrt {2}}\;\left({\sqrt {5}}-1\right)\right]\,}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/96ed3130d2995af89ffd7fed92ca75b79e11b580)








![{\displaystyle \sin {\frac {\pi }{5}}=\sin 36^{\circ }={\tfrac {1}{4}}\left[{\sqrt {2\left(5-{\sqrt {5}}\right)}}\right]\,}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/a5a125bab3d72d8e6ca59b000aa0de58afe4e645)




![{\displaystyle \tan {\frac {13\pi }{60}}=\tan 39^{\circ }={\tfrac {1}{4}}\left[\left(2-{\sqrt {3}}\right)\left(3-{\sqrt {5}}\right)-2\right]\left[2-{\sqrt {2\left(5+{\sqrt {5}}\right)}}\right]\,}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/3f5d40feb83e05d4be7784892beb0641f8740e59)

























![{\displaystyle {\frac {1}{2}}{\sqrt {{\frac {1}{3}}\left(7-\omega ^{2}{\sqrt[{3}]{\frac {7+21{\sqrt {-3}}}{2}}}-\omega {\sqrt[{3}]{\frac {7-21{\sqrt {-3}}}{2}}}\right)}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/8cc7dc542d7b26bf260027485f6a30538ffeffed)
![{\displaystyle {\frac {1}{6}}\left(-1+{\sqrt[{3}]{\frac {7+21{\sqrt {-3}}}{2}}}+{\sqrt[{3}]{\frac {7-21{\sqrt {-3}}}{2}}}\right)}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/b9770256721ca5edf98ee18d025cdcea444febf4)












![{\displaystyle {\frac {1}{4}}\left({\sqrt[{3}]{4i-4{\sqrt {3}}}}-{\sqrt[{3}]{4i+4{\sqrt {3}}}}\right)}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/831ad9c69d6f77d8090366aa50615a1542b2dfbc)
![{\displaystyle {\frac {1}{4}}\left({\sqrt[{3}]{4+4i{\sqrt {3}}}}+{\sqrt[{3}]{4-4i{\sqrt {3}}}}\right)}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/5b255f026730e4fe89ed9015dbb49d3216e5353e)




