不连续点:修订间差异
外观
删除的内容 添加的内容
svg (GlobalReplace v0.6.5) |
TheNewHope(留言 | 贡献) |
||
| 第1行: | 第1行: | ||
{{微积分学}} |
{{微积分学}} |
||
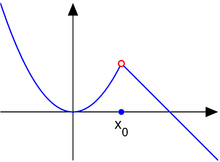
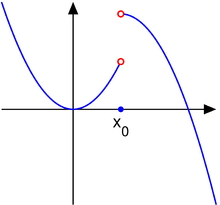
'''不连续点'''又称'''间断点''',通常是在單變數實值函數的環境下討論。令<math>E\subseteq \mathbb{R},~f:E\to\mathbb{R}</math>,且若<math>c\in\mathbb{R}</math>(不一定要在<math>E</math>中),若<math>f</math>在<math>c</math>不連續,則稱<math>f</math>在那裡有個不連續點、<math>c</math>為一個<math>f</math>的不連續點。 |
'''不连续点'''又称'''间断点''',通常是在單變數實值函數的環境下討論。令<math>E\subseteq \mathbb{R},~f:E\to\mathbb{R}</math>,且若<math>c\in\mathbb{R}</math>(不一定要在<math>E</math>中),若<math>f</math>在<math>c</math>不連續,則稱<math>f</math>在那裡有個不連續點、<math>c</math>為一個<math>f</math>的不連續點。 |
||
关于复变函数的奇点的分类,请参考[[奇点_(数学)]]。 |
|||
== 分类 == |
== 分类 == |
||