C3线性化:修订间差异
补救9个来源,并将0个来源标记为失效。) #IABot (v2.0.8) (Yining Chen - 8470 |
|||
| 第24行: | 第24行: | ||
| archive-url = https://web.archive.org/web/20181214001931/http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.19.3910&rep=rep1&type=pdf |
| archive-url = https://web.archive.org/web/20181214001931/http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.19.3910&rep=rep1&type=pdf |
||
| dead-url = no |
| dead-url = no |
||
}}</ref>首次提出了C3超类线性化。它被[[Python]] 2.3<ref>{{Cite web |url=https://www.python.org/download/releases/2.3/mro/ |title=Python 2.3's use of C3 MRO |accessdate=2018-02-02 |archive-date=2020-08-20 |archive-url=https://web.archive.org/web/20200820231854/https://www.python.org/download/releases/2.3/mro/ |dead-url=no }}</ref><ref>{{Cite web |url=http://rhettinger.wordpress.com/2011/05/26/super-considered-super/ |title=Tutorial for practical applications of C3 linearization using Python |accessdate=2018-02-02 |archive-date=2020-07-05 |archive-url=https://web.archive.org/web/20200705054428/https://rhettinger.wordpress.com/2011/05/26/super-considered-super/ |dead-url=no }}</ref>、[[Perl 6]]<ref>{{Cite web |url=http://doc.perl6.org/type/Metamodel::C3MRO |title=Perl 6's use of the C3 MRO |accessdate=2018-02-02 |archive-date=2016-06-17 |archive-url=https://web.archive.org/web/20160617001030/http://doc.perl6.org/type/Metamodel::C3MRO |dead-url=no }}</ref>、[[Parrot虚拟机|Parrot]]<ref>{{Cite web |url=http://aspn.activestate.com/ASPN/Mail/Message/perl6-internals/2746631 |title=Parrot uses C3 MRO |access-date=2018-02-02 |archive-url=https://web.archive.org/web/20070208165958/http://aspn.activestate.com/ASPN/Mail/Message/perl6-internals/2746631 |archive-date=2007-02-08 |dead-url=yes }}</ref>、[[Solidity]]和{{tsl|en|PGF/TikZ}}的面向对象语言模块<ref>{{cite book|last1=Tantau|first1=Till|title=The TikZ & PGF Manual|date=2015-08-29|page=956|edition=3.0.1a|url=http://ftp.ntua.gr/mirror/ctan/graphics/pgf/base/doc/pgfmanual.pdf|accessdate=2017-08-14|archive-date=2020-08-26|archive-url=https://web.archive.org/web/20200826223205/http://ftp.ntua.gr/mirror/ctan/graphics/pgf/base/doc/pgfmanual.pdf|dead-url=no}}</ref>等,选作方法解析的默认算法。[[Perl|Perl 5]]语言从版本5.10.0起将它作为可选的、非默认的MRO<ref>{{Cite web |url=https://metacpan.org/module/mro |title=C3 MRO available in Perl 5.10 and newer |accessdate=2018-02-02 |archive-date=2013-09-13 |archive-url=https://web.archive.org/web/20130913023639/https://metacpan.org/module/mro |dead-url=no }}</ref>。早期版本Perl 5有称为<code>Class::C3</code>一个扩展实现曾发布于[[CPAN]]<ref>{{Cite web |url=https://metacpan.org/module/Class::C3 |title=Perl 5 extension for C3 MRO on CPAN |accessdate=2018-02-02 |archive-date=2013-06-06 |archive-url=https://web.archive.org/web/20130606070211/https://metacpan.org/module/Class::C3 |dead-url=no }}</ref>。 |
|||
}}</ref>首次提出了C3超类线性化。它被[[Python]] 2.3<ref> |
|||
{{Cite web |url=https://www.python.org/download/releases/2.3/mro/ |title=Python 2.3's use of C3 MRO |accessdate=2018-02-02 |archive-date=2020-08-20 |archive-url=https://web.archive.org/web/20200820231854/https://www.python.org/download/releases/2.3/mro/ |dead-url=no }}</ref><ref>{{Cite web |url=http://rhettinger.wordpress.com/2011/05/26/super-considered-super/ |title=Tutorial for practical applications of C3 linearization using Python |accessdate=2018-02-02 |archive-date=2020-07-05 |archive-url=https://web.archive.org/web/20200705054428/https://rhettinger.wordpress.com/2011/05/26/super-considered-super/ |dead-url=no }} |
|||
</ref>、[[Perl 6]]<ref> |
|||
{{Cite web |url=http://doc.perl6.org/type/Metamodel::C3MRO |title=Perl 6's use of the C3 MRO |accessdate=2018-02-02 |archive-date=2016-06-17 |archive-url=https://web.archive.org/web/20160617001030/http://doc.perl6.org/type/Metamodel::C3MRO |dead-url=no }} |
|||
</ref>、[[Parrot虚拟机|Parrot]]<ref> |
|||
{{Cite web |url=http://aspn.activestate.com/ASPN/Mail/Message/perl6-internals/2746631 |title=Parrot uses C3 MRO |access-date=2018-02-02 |archive-url=https://web.archive.org/web/20070208165958/http://aspn.activestate.com/ASPN/Mail/Message/perl6-internals/2746631 |archive-date=2007-02-08 |dead-url=yes }} |
|||
</ref>、[[Solidity]]和{{tsl|en|PGF/TikZ}}的面向对象语言模块<ref> |
|||
{{cite book|last1=Tantau|first1=Till|title=The TikZ & PGF Manual|date=2015-08-29|page=956|edition=3.0.1a|url=http://ftp.ntua.gr/mirror/ctan/graphics/pgf/base/doc/pgfmanual.pdf|accessdate=2017-08-14|archive-date=2020-08-26|archive-url=https://web.archive.org/web/20200826223205/http://ftp.ntua.gr/mirror/ctan/graphics/pgf/base/doc/pgfmanual.pdf|dead-url=no}} |
|||
</ref>等,选作方法解析的默认算法。[[Perl|Perl 5]]语言从版本5.10.0起将它作为可选的、非默认的MRO<ref> |
|||
{{Cite web |url=https://metacpan.org/module/mro |title=C3 MRO available in Perl 5.10 and newer |accessdate=2018-02-02 |archive-date=2013-09-13 |archive-url=https://web.archive.org/web/20130913023639/https://metacpan.org/module/mro |dead-url=no }} |
|||
</ref>。早期版本Perl 5有称为<code>Class::C3</code>一个扩展实现曾发布于[[CPAN]]<ref> |
|||
{{Cite web |url=https://metacpan.org/module/Class::C3 |title=Perl 5 extension for C3 MRO on CPAN |accessdate=2018-02-02 |archive-date=2013-06-06 |archive-url=https://web.archive.org/web/20130606070211/https://metacpan.org/module/Class::C3 |dead-url=no }}</ref>。 |
|||
== 描述 == |
== 描述 == |
||
2021年8月9日 (一) 12:41的版本
在计算机科学中,C3算法主要用在多重继承中,确定子类应该继承哪一个父类的方法。换句话说,C3超类线性化的输出是确定性的方法解析顺序(MRO:Method Resolution Order)。
C3算法得名于它实现了一致性于三种重要特性:
- 扩展的优先图,
- 局部优先原则(比如A继承B和C,C继承B,那么A读取父类方法,应该优先使用C的方法而不是B的方法),
- 单调性原则(即子类不改变父类的方法搜索顺序)。
在1996年的OOPSLA会议上,发表的论文《A Monotonic Superclass Linearization for Dylan》[1]首次提出了C3超类线性化。它被Python 2.3[2][3]、Perl 6[4]、Parrot[5]、Solidity和PGF/TikZ的面向对象语言模块[6]等,选作方法解析的默认算法。Perl 5语言从版本5.10.0起将它作为可选的、非默认的MRO[7]。早期版本Perl 5有称为Class::C3一个扩展实现曾发布于CPAN[8]。
描述
一个类的C3超类线性化是这个类,再加上它的各个父类的线性化与各个父类形成列表的唯一合并的结果。父类列表作为合并过程的最后实参,保持了直接父类的本地前趋序。
各个父类的线性化与各个父类形成列表的合并算法,首先选择不出现在各个列表的尾部(指除了第一个元素外的其他元素)的第一个元素,该元素可能同时出现在多个列表的头部。被选中元素从各个列表中删除并追加到输出列表中。这个选择再删除、追加元素的过程迭代下去直到各个列表被耗尽。如果在某个时候无法选出元素,说明这个类继承体系的依赖序是不一致的,因而无法线性化。[9]
例子
给定
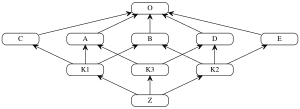
class O class A extends O class B extends O class C extends O class D extends O class E extends O class K1 extends A, B, C class K2 extends D, B, E class K3 extends D, A class Z extends K1, K2, K3
Z的线性化计算:
L(O) := [O] // the linearization of O is trivially the singleton list [O], because O has no parents
L(A) := [A] + merge(L(O), [O]) // the linearization of A is A plus the merge of its parents' linearizations with the list of parents...
= [A] + merge([O], [O])
= [A, O] // ...which simply prepends A to its single parent's linearization
L(B) := [B, O] // linearizations of B, C, D and E are computed similar to that of A
L(C) := [C, O]
L(D) := [D, O]
L(E) := [E, O]
L(K1) := [K1] + merge(L(A), L(B), L(C), [A, B, C]) // first, find the linearizations of K1's parents, L(A), L(B), and L(C), and merge them with the parent list [A, B, C]
= [K1] + merge([A, O], [B, O], [C, O], [A, B, C]) // class A is a good candidate for the first merge step, because it only appears as the head of the first and last lists
= [K1, A] + merge([O], [B, O], [C, O], [B, C]) // class O is not a good candidate for the next merge step, because it also appears in the tails of list 2 and 3; but class B is a good candidate
= [K1, A, B] + merge([O], [O], [C, O], [C]) // class C is a good candidate; class O still appears in the tail of list 3
= [K1, A, B, C] + merge([O], [O], [O]) // finally, class O is a valid candidate, which also exhausts all remaining lists
= [K1, A, B, C, O]
L(K2) := [K2] + merge(L(D), L(B), L(E), [D, B, E])
= [K2] + merge([D, O], [B, O], [E, O], [D, B, E]) // select D
= [K2, D] + merge([O], [B, O], [E, O], [B, E]) // fail O, select B
= [K2, D, B] + merge([O], [O], [E, O], [E]) // fail O, select E
= [K2, D, B, E] + merge([O], [O], [O]) // select O
= [K2, D, B, E, O]
L(K3) := [K3] + merge(L(D), L(A), [D, A])
= [K3] + merge([D, O], [A, O], [D, A]) // select D
= [K3, D] + merge([O], [A, O], [A]) // fail O, select A
= [K3, D, A] + merge([O], [O]) // select O
= [K3, D, A, O]
L(Z) := [Z] + merge(L(K1), L(K2), L(K3), [K1, K2, K3])
= [Z] + merge([K1, A, B, C, O], [K2, D, B, E, O], [K3, D, A, O], [K1, K2, K3]) // select K1
= [Z, K1] + merge([A, B, C, O], [K2, D, B, E, O], [K3, D, A, O], [K2, K3]) // fail A, select K2
= [Z, K1, K2] + merge([A, B, C, O], [D, B, E, O], [K3, D, A, O], [K3]) // fail A, fail D, select K3
= [Z, K1, K2, K3] + merge([A, B, C, O], [D, B, E, O], [D, A, O]) // fail A, select D
= [Z, K1, K2, K3, D] + merge([A, B, C, O], [B, E, O], [A, O]) // select A
= [Z, K1, K2, K3, D, A] + merge([B, C, O], [B, E, O], [O]) // select B
= [Z, K1, K2, K3, D, A, B] + merge([C, O], [E, O], [O]) // select C
= [Z, K1, K2, K3, D, A, B, C] + merge([O], [E, O], [O]) // fail O, select E
= [Z, K1, K2, K3, D, A, B, C, E] + merge([O], [O], [O]) // select O
= [Z, K1, K2, K3, D, A, B, C, E, O] // done
例子的 Python 实现
以下为 C3 算法 Python 实现的一个例子
def c3_mro(cls):
if cls is object:
# 讨论假设顶层基类为 object ,递归终止
return [object]
# 构造 C3-MRO 算法的总式,递归开始
merge_list = [c3_mro(base_cls) for base_cls in cls.__bases__]
merge_list.append(list(cls.__bases__))
mro = [cls] + merge(merge_list)
return mro
def merge(in_lists):
if not in_lists:
# 若合并的内容为空,返回空 list
# 配合下文的排除空 list 操作,递归终止
return []
# 遍历要合并的 MRO
for mro_list in in_lists:
# 取头
head = mro_list[0]
# 遍历要合并的 MRO(与外一层相同),检查尾中是否有头
for cmp_list in in_lists:
if cmp_list is mro_list:
continue
if head in cmp_list[1:]:
break
else:
# 筛选出好头
next_list = []
for merge_item in in_lists:
if head in merge_item:
merge_item.remove(head)
if merge_item:
# 排除空 list
next_list.append(merge_item)
# 递归开始
return [head] + merge(next_list)
else:
# 无好头,引发类型错误
raise TypeError
首先,metaclass 允许对象通过名字简明表示而不用 <class '__main__.A'>:
class Type(type):
def __repr__(cls):
return cls.__name__
A = Type('A', (object,), {})
类 A 表示自身通过名字:
>>> A
A
由于 Python 3 的metaclass语法改变了,为使例子兼任版本2与3,用metaclass创建对象,如同用type。
A = Type('A', (object,), {})
B = Type('B', (object,), {})
C = Type('C', (object,), {})
D = Type('D', (object,), {})
E = Type('E', (object,), {})
K1 = Type('K1', (A, B, C), {})
K2 = Type('K2', (D, B, E), {})
K3 = Type('K3', (D, A), {})
Z = Type('Z', (K1, K2, K3), {})
等价的Python 2 的类定义是:
class Z(K1, K2, K3):
__metaclass__ = Type
对于Python 3是
class Z(K1, K2, K3, metaclass=Type):
pass
最后有:
>>> Z.mro()
[Z, K1, K2, K3, D, A, B, C, E, <type 'object'>]
参考文献
- ^ A Monotonic Superclass Linearization for Dylan. OOPSLA '96 Conference Proceedings. ACM Press: 69–82. 1996-06-28 [2018-02-02]. ISBN 0-89791-788-X. doi:10.1145/236337.236343. (原始内容存档于2018-12-14).
- ^ Python 2.3's use of C3 MRO. [2018-02-02]. (原始内容存档于2020-08-20).
- ^ Tutorial for practical applications of C3 linearization using Python. [2018-02-02]. (原始内容存档于2020-07-05).
- ^ Perl 6's use of the C3 MRO. [2018-02-02]. (原始内容存档于2016-06-17).
- ^ Parrot uses C3 MRO. [2018-02-02]. (原始内容存档于2007-02-08).
- ^ Tantau, Till. The TikZ & PGF Manual (PDF) 3.0.1a. 2015-08-29: 956 [2017-08-14]. (原始内容存档 (PDF)于2020-08-26).
- ^ C3 MRO available in Perl 5.10 and newer. [2018-02-02]. (原始内容存档于2013-09-13).
- ^ Perl 5 extension for C3 MRO on CPAN. [2018-02-02]. (原始内容存档于2013-06-06).
- ^ van Rossum, Guido. Method Resolution Order. The History of Python. 2010-06-23 [2018-01-18]. (原始内容存档于2018-02-08).
