第429行:
第429行:
可以在[[反三角函数]]条目中找到类似的公式。使用复[[对数]],可以把这些函数推广到复辐角上:
可以在[[反三角函数]]条目中找到类似的公式。使用复[[对数]],可以把这些函数推广到复辐角上:
:<math>
:<math>
\arcsin (z) = -i \log \left( i z + \sqrt{1 - z^2} \right)
\arcsin (z) = -i \ln \left( i z + \sqrt{1 - z^2} \right)
</math>
</math>
:<math>
:<math>
\arccos (z) = -i \log \left( z + \sqrt{z^2 - 1}\right)
\arccos (z) = -i \ln \left( z + \sqrt{z^2 - 1}\right)
</math>
</math>
:<math>
:<math>
\arctan (z) = \frac{i}{2} \log\left(\frac{1-iz}{1+iz}\right)
\arctan (z) = \frac{i}{2} \ln \left(\frac{1-iz}{1+iz}\right)
</math>
</math>
<!-- (note: these should probably be presented as definite integrals, removing the ambiguity of the constant) -->
<!-- (note: these should probably be presented as definite integrals, removing the ambiguity of the constant) -->
角 θ的所有三角函数在几何上可以依据以O 點為圓心的单位圓来构造。 三角函数: 正弦 , 餘弦 , 正切 , 正割 , 餘割 , 餘切 在数学 中,三角函数 (也叫做圆函数)是角 的函数 ;它们在研究三角形 和建模周期现象和许多其他应用中是很重要的。三角函数通常定义为包含这个角的直角三角形的两个边的比率 ,也可以等价的定义为单位圆 上的各种线段的长度。更现代的定义把它们表达为无穷级数 或特定微分方程 的解,允许它们扩展到任意正数和负数值,甚至是复数 值。
三角函数在数学 中属于初等函数 裡的超越函数 的一类函数。它们的本质是任意角 的集合与一个比值的集合的变量之间的映射 。由于三角函数表現出周期性,所以它并不具有单射函数 意义上的反函数 。三角函数在复数 中有较为重要的应用。在物理学中,三角函数也是常用的工具。
函数 简写 关系
正弦 sin
sin
θ
=
cos
(
π
2
−
θ
)
=
1
csc
θ
{\displaystyle \sin \theta =\cos \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\csc \theta }}\,}
餘弦 cos
cos
θ
=
sin
(
π
2
−
θ
)
=
1
sec
θ
{\displaystyle \cos \theta =\sin \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\sec \theta }}\,}
正切
tan
tan
θ
=
sin
θ
cos
θ
=
cot
(
π
2
−
θ
)
=
1
cot
θ
{\displaystyle \tan \theta ={\frac {\sin \theta }{\cos \theta }}=\cot \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\cot \theta }}\,}
餘割
csc
csc
θ
=
sec
(
π
2
−
θ
)
=
1
sin
θ
{\displaystyle \csc \theta =\sec \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\sin \theta }}\,}
正割
sec
sec
θ
=
csc
(
π
2
−
θ
)
=
1
cos
θ
{\displaystyle \sec \theta =\csc \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\cos \theta }}\,}
餘切
cot
cot
θ
=
cos
θ
sin
θ
=
tan
(
π
2
−
θ
)
=
1
tan
θ
{\displaystyle \cot \theta ={\frac {\cos \theta }{\sin \theta }}=\tan \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\tan \theta }}\,}
除六個基本函數,历史上還有下面六个函数:
正矢
versin
(
θ
)
=
1
−
cos
(
θ
)
=
2
sin
2
(
θ
2
)
{\displaystyle {\textrm {versin}}(\theta )=1-\cos(\theta )=2\sin ^{2}\left({\frac {\theta }{2}}\right)\,}
餘矢
coversin
(
θ
)
=
versin
(
π
/
2
−
θ
)
=
1
−
sin
(
θ
)
{\displaystyle {\textrm {coversin}}(\theta )={\textrm {versin}}(\pi /2-\theta )=1-\sin(\theta )\,}
半正矢
haversin
(
θ
)
=
versin
(
θ
)
2
=
sin
2
(
θ
2
)
{\displaystyle {\textrm {haversin}}(\theta )={\frac {{\textrm {versin}}(\theta )}{2}}=\sin ^{2}\left({\frac {\theta }{2}}\right)}
半餘矢
hacoversin
(
θ
)
=
haversin
(
π
2
−
θ
)
=
coversin
(
θ
)
2
{\displaystyle {\textrm {hacoversin}}(\theta )={\textrm {haversin}}\left({\frac {\pi }{2}}-\theta \right)={\frac {{\textrm {coversin}}(\theta )}{2}}}
外正割
exsec
(
θ
)
=
sec
(
θ
)
−
1
{\displaystyle {\textrm {exsec}}(\theta )=\sec(\theta )-1\,}
外餘割
excsc
(
θ
)
=
exsec
(
π
/
2
−
θ
)
=
csc
(
θ
)
−
1
{\displaystyle {\textrm {excsc}}(\theta )={\textrm {exsec}}(\pi /2-\theta )=\csc(\theta )-1\!}
随着认识到相似三角形在它们的边之间保持相同的比率,就有了在三角形的边的长度和三角形的角之间应当有某种标准的对应的想法。就是说对于任何相似三角形,(比如)斜边和剩下的两个边的比率都是相同的。如果斜边变为两倍长,其他边也要变为两倍长。三角函数表达的就是这些比率。
研究三角函数的有尼西亚 的喜帕恰斯 (公元前180-125年)、埃及 的托勒密 (公元90-180年)、Aryabhata (公元476-550年),Varahamihira 、婆罗摩笈多 、花拉子密 、Abū al-Wafā' al-Būzjānī 、欧玛尔·海亚姆 、婆什迦罗第二 、Nasir al-Din al-Tusi 、Ghiyath al-Kashi (14世纪)、Ulugh Beg (14世纪)、约翰·缪勒 (1464)、Rheticus 和 Rheticus 的学生 Valentin Otho。
Madhava of Sangamagramma (約1400)以无穷级数 的方式做了三角函数的分析 的早期研究。欧拉 的《無窮微量解析入門 》(Introductio in Analysin Infinitorum )(1748)对建立三角函数在欧洲的分析处理做了最主要的贡献,他定义三角函数为无穷级数,并表述了欧拉公式 ,还有使用接近现代的简写 sin. 、cos. 、tang. 、cot. 、sec. 和 cosec. 。
File:Tri def.png 在直角三角形 中仅有锐角 三角函数的定义。
一个锐角的正弦 是它的对边与斜边的比值。在图中,
sin
A
{\displaystyle \sin A}
a /h 。 一个锐角的餘弦 是它的邻边与斜边的比值。在图中,
cos
A
{\displaystyle \cos A}
b /h 。 一个锐角的正切 是它的对边与邻边的比值。在图中,
tan
A
{\displaystyle \tan A}
a /b 。
设α是平面直角坐标系xOy中的一个象限角 ,
P
(
x
,
y
)
{\displaystyle P\left({x,y}\right)}
r
=
x
2
+
y
2
>
0
{\displaystyle r={\sqrt {x^{2}+y^{2}}}>0}
函数名
定义
函数名
定义
正弦
sin
α
=
y
r
{\displaystyle \sin \alpha ={\frac {y}{r}}}
餘弦
cos
α
=
x
r
{\displaystyle \cos \alpha ={\frac {x}{r}}}
正切
tan
α
=
y
x
{\displaystyle \tan \alpha ={\frac {y}{x}}}
餘切
cot
α
=
x
y
{\displaystyle \cot \alpha ={\frac {x}{y}}}
正割
sec
α
=
r
x
{\displaystyle \sec \alpha ={\frac {r}{x}}}
餘割
csc
α
=
r
y
{\displaystyle \csc \alpha ={\frac {r}{y}}}
单位圆 六个三角函数也可以依据半径为一中心为原点的单位圆 来定义。单位圆定义在实际计算上没有大的价值;实际上对多数角它都依赖于直角三角形。但是单位圆定义的确允许三角函数对所有正数和负数辐角都有定义,而不只是对于在 0 和 π/2 弧度之间的角。它提供了一个单一的可视图像,一次封装了所有重要的三角函数。根据勾股定理 ,单位圆的等式是:
x
2
+
y
2
=
1
{\displaystyle x^{2}+y^{2}=1\,}
在图像中,给出了用弧度度量的某个公共角。逆时针方向的度量是正角而顺时针的度量是负角。设一个过原点的线,同 x 轴正半部分得到一个角 θ ,并与单位圆相交。这个交点的 x 和 y 坐标分别等于 cos θ 和 sin θ 。在这个图形中的三角形确保了这个公式;半径等于斜边并有长度 1,所以有了 sin θ = y /1 和 cos θ = x /1。单位圆可以被視为是通过改变邻边和对边的长度,并保持斜边等于 1,查看无限個三角形的一种方式。
在笛卡尔平面上 f (x ) = sin(x ) 和 f (x ) = cos(x ) 函数的图像。 对于大于 2π 或小于 −2π 的角度,简单的继续绕单位圆旋转。在这种方式下,正弦和余弦变成了周期为 2π的周期函数 :
sin
θ
=
sin
(
θ
+
2
π
k
)
{\displaystyle \sin \theta =\sin \left(\theta +2\pi k\right)}
cos
θ
=
cos
(
θ
+
2
π
k
)
{\displaystyle \cos \theta =\cos \left(\theta +2\pi k\right)}
对于任何角度 θ 和任何整数 k 。
周期函数的最小正周期叫做这个函数的“基本周期”(primitive period)。正弦、余弦、正割或余割的基本周期是全圆,也就是 2π 弧度或 360 度;正切或余切的基本周期是半圆,也就是 π 弧度或 180 度。上面只有正弦和余弦是直接使用单位圆定义的,其他四个三角函数可以定义为:
tan
θ
=
sin
θ
cos
θ
sec
θ
=
1
cos
θ
{\displaystyle \tan \theta ={\frac {\sin \theta }{\cos \theta }}\quad \sec \theta ={\frac {1}{\cos \theta }}}
csc
θ
=
1
sin
θ
cot
θ
=
cos
θ
sin
θ
{\displaystyle \csc \theta ={\frac {1}{\sin \theta }}\quad \cot \theta ={\frac {\cos \theta }{\sin \theta }}}
在笛卡尔平面上 f (x ) = tan(x ) 函数的图像。 在正切函数的图像中,在角 k π 附近变化缓慢,而在接近角 (k + 1/2)π 的时候变换迅速。正切函数的图像在 θ = (k + 1/2)π 有垂直渐进线 。这是因为在 θ 从左侧接进 (k + 1/2)π 的时候函数接近正无穷,而从右侧接近 (k + 1/2)π 的时候函数接近负无穷。
可作为替代选择,所有基本三角函数都可依据中心为 O 的单位圆来定义,类似于历史上使用的几何定义。特别是,对于这个圆的弦 AB ,这里的 θ 是对向角的一半,sin(θ) 是 AC (半弦),这是印度 的 Aryabhata (AD 476–550)介入的定义。cos(θ) 是水平距离 OC ,versin (θ) = 1 − cos(θ) 是 CD 。tan(θ) 是通过 A 的切线 的线段 AE 的长度,所以这个函数才叫正切。cot(θ) 是另一个切线段 AF 。 sec(θ) = OE 和 csc(θ) = OF 是割线 (与圆相交于两点)的线段,所以可以看作 OA 沿着 A 的切线分别向水平和垂直轴的投影。DE 是 exsec (θ) = sec(θ) − 1 (正割在圆外的部分)。通过这些构造,容易看出正割和正切函数在 θ 接近 π/2 (90 度)的时候发散,而余割和余切在 θ 接近零的时候发散。
正弦函数(蓝色)被对中心为原点的全圆的它的 5 次泰勒级数(粉红色)紧密逼近。 只使用几何和极限 的性质,可以证明正弦的导数 是余弦,而余弦的导数是负的正弦。(在微积分 中,所有角度都以弧度 来度量)。你可以接着使用泰勒级数 的理论来证明下列恒等式对于所有实数 x 都成立 :
sin
x
=
x
−
x
3
3
!
+
x
5
5
!
−
x
7
7
!
+
⋯
=
∑
n
=
0
∞
(
−
1
)
n
x
2
n
+
1
(
2
n
+
1
)
!
{\displaystyle \sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}}}
cos
x
=
1
−
x
2
2
!
+
x
4
4
!
−
x
6
6
!
+
⋯
=
∑
n
=
0
∞
(
−
1
)
n
x
2
n
(
2
n
)
!
{\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}}
这些恒等式经常被用做正弦和余弦函数的定义。它们经常被用做三角函数的严肃处理和应用的起点(比如,在傅立叶级数 中),因为无穷级数 的理论自实数系 的基础上发展而来,独立于任何几何考虑。这些函数的可微性 和连续性 经常单独从级数定义自身确立。
其他级数可见于:[ 1]
tan
x
{\displaystyle \tan x\,}
=
∑
n
=
0
∞
U
2
n
+
1
x
2
n
+
1
(
2
n
+
1
)
!
{\displaystyle {}=\sum _{n=0}^{\infty }{\frac {U_{2n+1}x^{2n+1}}{(2n+1)!}}}
=
∑
n
=
1
∞
(
−
1
)
n
−
1
2
2
n
(
2
2
n
−
1
)
B
2
n
x
2
n
−
1
(
2
n
)
!
{\displaystyle {}=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}}}
=
x
+
x
3
3
+
2
x
5
15
+
17
x
7
315
+
⋯
,
for
|
x
|
<
π
2
{\displaystyle {}=x+{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}+{\frac {17x^{7}}{315}}+\cdots ,\qquad {\mbox{for }}|x|<{\frac {\pi }{2}}}
这里的
U
n
{\displaystyle U_{n}\,}
n 次上/下数 ,
B
n
{\displaystyle B_{n}\,}
n 次伯努利数 ,
E
n
{\displaystyle E_{n}\,}
n 次欧拉数 。在这种形式的表达中,分母是相应的阶乘,而分子叫做“正切数”,有组合 解释: 它们枚举了奇数势 的有限集合的交错排列 (alternating permutation)。
csc
x
{\displaystyle \csc x\,}
=
∑
n
=
0
∞
(
−
1
)
n
+
1
2
(
2
2
n
−
1
−
1
)
B
2
n
x
2
n
−
1
(
2
n
)
!
{\displaystyle {}=\sum _{n=0}^{\infty }{\frac {(-1)^{n+1}2(2^{2n-1}-1)B_{2n}x^{2n-1}}{(2n)!}}}
=
1
x
+
x
6
+
7
x
3
360
+
31
x
5
15120
+
⋯
,
for
0
<
|
x
|
<
π
{\displaystyle {}={\frac {1}{x}}+{\frac {x}{6}}+{\frac {7x^{3}}{360}}+{\frac {31x^{5}}{15120}}+\cdots ,\qquad {\mbox{for }}0<|x|<\pi }
sec
x
{\displaystyle \sec x\,}
=
∑
n
=
0
∞
U
2
n
x
2
n
(
2
n
)
!
=
∑
n
=
0
∞
(
−
1
)
n
E
n
x
2
n
(
2
n
)
!
{\displaystyle {}=\sum _{n=0}^{\infty }{\frac {U_{2n}x^{2n}}{(2n)!}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}E_{n}x^{2n}}{(2n)!}}}
=
1
+
x
2
2
+
5
x
4
24
+
61
x
6
720
+
⋯
,
for
|
x
|
<
π
2
{\displaystyle {}=1+{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}+{\frac {61x^{6}}{720}}+\cdots ,\qquad {\mbox{for }}|x|<{\frac {\pi }{2}}}
在这种形式的表达中,分母是对应的阶乘,而分子叫做“正割数”,有组合 解释: 它们枚举偶数势的有限集合的交错排列。
cot
x
{\displaystyle \cot x\,}
=
∑
n
=
0
∞
(
−
1
)
n
2
2
n
B
2
n
x
2
n
−
1
(
2
n
)
!
{\displaystyle {}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}2^{2n}B_{2n}x^{2n-1}}{(2n)!}}}
=
1
x
−
x
3
−
x
3
45
−
2
x
5
945
−
⋯
,
for
0
<
|
x
|
<
π
{\displaystyle {}={\frac {1}{x}}-{\frac {x}{3}}-{\frac {x^{3}}{45}}-{\frac {2x^{5}}{945}}-\cdots ,\qquad {\mbox{for }}0<|x|<\pi }
从复分析 的一个定理得出,这个实函数到复数有一个唯一的解析扩展(analytic extension)。它们有同样的泰勒级数,所以定义在复数上三角函数使用上述泰勒级数。
复正弦。横轴对应函数自变量实部,纵轴对应函数自变量虚部,色相 表示函数的幅角,而亮度 表示函数的幅值。 复余弦。横轴对应函数自变量实部,纵轴对应函数自变量虚部,色相 表示函数的幅角,而亮度 表示函数的幅值。 可以从上述的级数定义证明正弦和余弦函数分别是复指数函数 在它的自变量为纯虚数 时候的虚数和实数部分:
e
i
θ
=
cos
θ
+
i
sin
θ
.
{\displaystyle e^{i\theta }=\cos \theta +i\sin \theta \,.}
这个联系首先由欧拉 注意到,而这个恒等式叫做欧拉公式 。在这种方式下,三角函数在复分析的几何解释中变成了本质性的。例如,通过上述恒等式,如果考虑在复平面 中 e ix 所定义的单位圆,同上面一样,我们可以依据余弦和正弦来参数化这个圆,在复指数和三角函数之间联系变得非常明显。
进一步的,这允许定义对复自变量 z 的三角函数:
sin
z
=
∑
n
=
0
∞
(
−
1
)
n
(
2
n
+
1
)
!
z
2
n
+
1
=
e
i
z
−
e
−
i
z
2
i
=
−
i
sinh
(
i
z
)
{\displaystyle \sin z\,=\,\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}z^{2n+1}\,=\,{e^{iz}-e^{-iz} \over 2i}=-i\sinh \left(iz\right)}
cos
z
=
∑
n
=
0
∞
(
−
1
)
n
(
2
n
)
!
z
2
n
=
e
i
z
+
e
−
i
z
2
=
cosh
(
i
z
)
{\displaystyle \cos z\,=\,\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}z^{2n}\,=\,{e^{iz}+e^{-iz} \over 2}=\cosh \left(iz\right)}
这里的 i 2 = −1。还有对于纯实数 x ,
cos
x
=
Re
(
e
i
x
)
{\displaystyle \cos x\,=\,{\mbox{Re }}(e^{ix})}
sin
x
=
Im
(
e
i
x
)
{\displaystyle \sin x\,=\,{\mbox{Im }}(e^{ix})}
还知道这种指数处理密切联系于周期行为。
正弦和余弦函数都满足微分方程
y
″
=
−
y
{\displaystyle y''=-y\,}
就是说,每个都是它自己的二阶导数的负数。在由所有这个方程的解的二维向量空间 V 中,正弦函数是满足初始条件 y (0) = 0 和 y ′(0) = 1 的唯一解,而余弦函数是满足初始条件 y (0) = 1 和 y ′(0) = 0 的唯一解。因为正弦和余弦函数是线性无关的,它们在一起形成了 V 的基 。这种定义正弦和余弦函数的方法本质上等价于使用欧拉公式。(参见线性微分方程 )。很明显这个微分方程不只用来定义正弦和余弦函数,还可用来证明正弦和余弦函数的三角恒等式 。进一步的,观察到正弦和余弦函数满足
y
″
=
−
y
{\displaystyle y''=-y\,}
特征函数 。
正切函数是非线性微分方程
y
′
=
1
+
y
2
{\displaystyle y'=1+y^{2}\,}
满足初始条件 y (0) = 0 的唯一解。有一个正切函数满足这个微分方程的非常有趣的可视证明;参见 Needham 的《Visual Complex Analysis》。[ 2]
弧度通过测量沿着单位圆的路径的长度指定一个角,并构成给正弦和余弦函数的特定辐角。特别是,只有映射弧度到比率的那些正弦和余弦函数才满足古典的描述它们的微分方程。如果给正弦和余弦函数的弧度辐角是正比于频率的
f
(
x
)
=
sin
(
k
x
)
;
k
≠
0
,
k
≠
1
{\displaystyle f(x)=\sin(kx);k\neq 0,k\neq 1\,}
则导数将正比于“振幅”。
f
′
(
x
)
=
k
cos
(
k
x
)
{\displaystyle f'(x)=k\cos(kx)\,}
这里的 k 是表示在单位之间映射的常数。如果 x 是度,则
k
=
π
180
∘
.
{\displaystyle k={\frac {\pi }{180^{\circ }}}.}
这意味着使用度的正弦的二阶导数不满足微分方程
y
″
=
−
y
{\displaystyle y''=-y\,}
而
y
″
=
−
k
2
y
{\displaystyle y''=-k^{2}y\,}
对余弦也是类似的。
这意味着这些正弦和余弦是不同的函数,因此正弦的四阶导数再次是正弦,只有它的辐角是弧度的条件下。
在三角函数相互之间存在很多恒等式。其中最常用的是毕达哥拉斯恒等式 ,它声称对于任何角,正弦的平方加上余弦的平方总是 1。这可从斜边为 1 的直角三角形应用毕达哥拉斯定理 得出。用符号形式表示,毕达哥拉斯恒等式为:
(
sin
x
)
2
+
(
cos
x
)
2
=
1
,
{\displaystyle \left(\sin x\right)^{2}+\left(\cos x\right)^{2}=1,}
更常写为在正弦和余弦符号之后加“2”次幂:
sin
2
(
x
)
+
cos
2
(
x
)
=
1.
{\displaystyle \sin ^{2}\left(x\right)+\cos ^{2}\left(x\right)=1.}
在某些情况下内层括号可以省略。
另一个关键联系是和差公式 ,它把两个角的和差的正弦和余弦依据这些角度自身的正弦和余弦而给出。它们可以在几何上使用托勒密 的论证方法推导出来;还可以在代数上使用欧拉公式 得出。
当两个角相同的时候,和公式简化为叫做二倍角公式 的更简单等式。
这些等式还可以用来推导积化和差恒等式 ,古代用它把两个数的积变换成两个数的和而像对数 那样做更快速的运算。
三角函数的积分 和导数 可参见导数表 、积分表 和三角函数积分表 。
在数学分析 中,可以基于和差公式这样的性质使用函数方程 来定义三角函数。例如,取用给定此种公式和毕达哥拉斯恒等式,可以证明只有两个实函数 满足这些条件。即存在唯一的一对实函数 sin 和 cos 使得对于所有实数 x 和 y ,下列方程成立:
sin
2
(
x
)
+
cos
2
(
x
)
=
1
,
{\displaystyle \sin ^{2}(x)+\cos ^{2}(x)=1,\,}
sin
(
x
+
y
)
=
sin
(
x
)
cos
(
y
)
+
cos
(
x
)
sin
(
y
)
,
{\displaystyle \sin(x+y)=\sin(x)\cos(y)+\cos(x)\sin(y),\,}
cos
(
x
+
y
)
=
cos
(
x
)
cos
(
y
)
−
sin
(
x
)
sin
(
y
)
,
{\displaystyle \cos(x+y)=\cos(x)\cos(y)-\sin(x)\sin(y),\,}
并满足附加条件
0
<
x
cos
(
x
)
<
sin
(
x
)
<
x
f
o
r
0
<
x
<
1
{\displaystyle 0<x\cos(x)<\sin(x)<x\ \mathrm {for} \ 0<x<1}
开始于其他函数方程的其他推导也是可能的,并且这种推导可以扩展到复数。作为例子,这个推导可以用来定义伽罗瓦域 中的三角学 。
三角函数的计算是个复杂的主题,由于计算机 和提供对任何角度的内置三角函数的科学计算器 的广泛使用,今天大多数人都幸免于此。本节中将描述它在三个重要上下文中的计算详情: 历史上使用的三角函数表,计算机使用的现代技术,和容易找到简单精确值的一些“重要”角度。(下面只考虑一个角度小范围,比如 0 到 π/2,因为通过三角函数的周期性和对称性,所有其他角度可以简约到这个范围内。)
在有计算机之前,人们典型的通过对计算到了多个有效数字 的一个三角函数值详表的内插 来计算三角函数的值。这种表格在有三角函数的描述的时候就已经有了,它们典型的是通过开始于已知值(比如sin(π/2)=1)的重复应用半角和和差公式而生成。
现代计算机使用了各种技术。[ 3] 浮点 单元的高端处理器上,是组合多项式 或有理式 逼近 (比如切比雪夫逼近 、最佳一致逼近和Padé逼近 ,和典型用于更高或可变精度的泰勒级数 和Laurent级数 )和范围简约与表查找 — 首先在一个小表中查找最近的角度,接着使用多项式来计算修正。[ 4] 硬件乘法器 的简单设备上,有叫做CORDIC算法 的一个更有效的算法(和相关技术),因为它只用了移位 和加法。出于性能的原因,所有这些方法通常都用硬件 来实现。
对于非常高精度的运算,在级数展开收敛变得太慢的时候,可以用算术几何平均 来逼近三角函数,它自身通过复数 椭圆积分 来逼近三角函数。[ 5]
最后对于一些简单的角度,可以如下面例子这样使用毕达哥拉斯定理 来手工计算三角函数的值。事实上,
π
/
60
{\displaystyle \pi /60}
弧度 (3°)的任何整数倍角的正弦、余弦和正切都可以手工找到。
考虑等腰直角三角形,两个角都是
π
/
4
{\displaystyle \pi /4}
b 和对边 a 的长度相等;我们可以选择
a
=
b
=
1
{\displaystyle a=b=1}
π
/
4
{\displaystyle \pi /4}
c
=
a
2
+
b
2
=
2
{\displaystyle c={\sqrt {a^{2}+b^{2}}}={\sqrt {2}}}
所以:
sin
(
π
/
4
)
=
sin
(
45
∘
)
=
cos
(
π
/
4
)
=
cos
(
45
∘
)
=
1
2
{\displaystyle \sin \left(\pi /4\right)=\sin \left(45^{\circ }\right)=\cos \left(\pi /4\right)=\cos \left(45^{\circ }\right)={1 \over {\sqrt {2}}}}
tan
(
π
/
4
)
=
tan
(
45
∘
)
=
sin
(
π
/
4
)
cos
(
π
/
4
)
=
1
2
⋅
2
1
=
2
2
=
1
{\displaystyle \tan \left(\pi /4\right)=\tan \left(45^{\circ }\right)={{\sin \left(\pi /4\right)} \over {\cos \left(\pi /4\right)}}={1 \over {\sqrt {2}}}\cdot {{\sqrt {2}} \over 1}={{\sqrt {2}} \over {\sqrt {2}}}=1}
要确定π/3弧度(60度)和π/6弧度(30度)角的三角函数,我们可以开始于边长为 1 的一个等边三角形,它的所有的角都是π/3弧度(60度)。把它等分为二,得到一个角是π/6弧度(30度)和一个角是π/3弧度(60度)的一个直角三角形。这个三角形中,最短的边 = 1/2、其次大的边 =(√3)/2 而斜边 = 1。得出:
sin
(
π
/
6
)
=
sin
(
30
∘
)
=
cos
(
π
/
3
)
=
cos
(
60
∘
)
=
1
2
{\displaystyle \sin \left(\pi /6\right)=\sin \left(30^{\circ }\right)=\cos \left(\pi /3\right)=\cos \left(60^{\circ }\right)={1 \over 2}}
cos
(
π
/
6
)
=
cos
(
30
∘
)
=
sin
(
π
/
3
)
=
sin
(
60
∘
)
=
3
2
{\displaystyle \cos \left(\pi /6\right)=\cos \left(30^{\circ }\right)=\sin \left(\pi /3\right)=\sin \left(60^{\circ }\right)={{\sqrt {3}} \over 2}}
tan
(
π
/
6
)
=
tan
(
30
∘
)
=
cot
(
π
/
3
)
=
cot
(
60
∘
)
=
1
3
{\displaystyle \tan \left(\pi /6\right)=\tan \left(30^{\circ }\right)=\cot \left(\pi /3\right)=\cot \left(60^{\circ }\right)={1 \over {\sqrt {3}}}}
三角函数中有一些常用的特殊函数值。
函數名
0
(
0
∘
)
{\displaystyle 0\ (0^{\circ })}
π
12
(
15
∘
)
{\displaystyle {\frac {\pi }{12}}\ (15^{\circ })}
π
6
(
30
∘
)
{\displaystyle {\frac {\pi }{6}}\ (30^{\circ })}
π
4
(
45
∘
)
{\displaystyle {\frac {\pi }{4}}\ (45^{\circ })}
π
3
(
60
∘
)
{\displaystyle {\frac {\pi }{3}}\ (60^{\circ })}
5
π
12
(
75
∘
)
{\displaystyle {\frac {5\pi }{12}}\ (75^{\circ })}
π
2
(
90
∘
)
{\displaystyle {\frac {\pi }{2}}\ (90^{\circ })}
sin
0
{\displaystyle 0}
6
−
2
4
{\displaystyle {\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}}
1
2
{\displaystyle {\frac {1}{2}}}
2
2
{\displaystyle {\frac {\sqrt {2}}{2}}}
3
2
{\displaystyle {\frac {\sqrt {3}}{2}}}
6
+
2
4
{\displaystyle {\frac {{\sqrt {6}}+{\sqrt {2}}}{4}}}
1
{\displaystyle 1}
cos
1
{\displaystyle 1}
6
+
2
4
{\displaystyle {\frac {{\sqrt {6}}+{\sqrt {2}}}{4}}}
3
2
{\displaystyle {\frac {\sqrt {3}}{2}}}
2
2
{\displaystyle {\frac {\sqrt {2}}{2}}}
1
2
{\displaystyle {\frac {1}{2}}}
6
−
2
4
{\displaystyle {\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}}
0
{\displaystyle 0}
tan
0
{\displaystyle 0}
2
−
3
{\displaystyle 2-{\sqrt {3}}}
3
3
{\displaystyle {\frac {\sqrt {3}}{3}}}
1
{\displaystyle 1}
3
{\displaystyle {\sqrt {3}}}
2
+
3
{\displaystyle 2+{\sqrt {3}}}
∞
{\displaystyle \infty }
cot
∞
{\displaystyle \infty }
2
+
3
{\displaystyle 2+{\sqrt {3}}}
3
{\displaystyle {\sqrt {3}}}
1
{\displaystyle 1}
3
3
{\displaystyle {\frac {\sqrt {3}}{3}}}
2
−
3
{\displaystyle 2-{\sqrt {3}}}
0
{\displaystyle 0}
sec
1
{\displaystyle 1}
6
−
2
{\displaystyle {\sqrt {6}}-{\sqrt {2}}}
2
3
3
{\displaystyle {\frac {2{\sqrt {3}}}{3}}}
2
{\displaystyle {\sqrt {2}}}
2
{\displaystyle 2}
6
+
2
{\displaystyle {\sqrt {6}}+{\sqrt {2}}}
∞
{\displaystyle \infty }
csc
∞
{\displaystyle \infty }
6
+
2
{\displaystyle {\sqrt {6}}+{\sqrt {2}}}
2
{\displaystyle 2}
2
{\displaystyle {\sqrt {2}}}
2
3
3
{\displaystyle {\frac {2{\sqrt {3}}}{3}}}
6
−
2
{\displaystyle {\sqrt {6}}-{\sqrt {2}}}
1
{\displaystyle 1}
由於三角函数屬於周期函数 ,而不是单射函数 ,所以严格來說並没有反函数 。因此要定义其反函数必须先限制三角函数的定义域 ,使得三角函数成為双射函数 。基本的反三角函数定义为:
反三角函数 定义 值域
arcsin
(
x
)
=
y
{\displaystyle \arcsin(x)=y\,}
sin
(
y
)
=
x
{\displaystyle \sin(y)=x\,}
−
π
2
≤
y
≤
π
2
{\displaystyle -{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}}\,}
arccos
(
x
)
=
y
{\displaystyle \arccos(x)=y\,}
cos
(
y
)
=
x
{\displaystyle \cos(y)=x\,}
0
≤
y
≤
π
{\displaystyle 0\leq y\leq \pi \,}
arctan
(
x
)
=
y
{\displaystyle \arctan(x)=y\,}
tan
(
y
)
=
x
{\displaystyle \tan(y)=x\,}
−
π
2
<
y
<
π
2
{\displaystyle -{\frac {\pi }{2}}<y<{\frac {\pi }{2}}\,}
arccsc
(
x
)
=
y
{\displaystyle \operatorname {arccsc}(x)=y\,}
csc
(
y
)
=
x
{\displaystyle \csc(y)=x\,}
−
π
2
≤
y
≤
π
2
,
y
≠
0
{\displaystyle -{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}},y\neq 0\,}
arcsec
(
x
)
=
y
{\displaystyle \operatorname {arcsec}(x)=y\,}
sec
(
y
)
=
x
{\displaystyle \sec(y)=x\,}
0
≤
y
≤
π
,
y
≠
π
2
{\displaystyle 0\leq y\leq \pi ,y\neq {\frac {\pi }{2}}\,}
arccot
(
x
)
=
y
{\displaystyle \operatorname {arccot}(x)=y\,}
cot
(
y
)
=
x
{\displaystyle \cot(y)=x\,}
0
<
y
<
π
{\displaystyle 0<y<\pi \,}
对于反三角函数,符号 sin−1 和 cos−1 经常用于 arcsin 和 arccos。当使用这种符号的时候,反函数可能混淆于这个函数的倒数。使用“arc-”前缀的符号避免了这种混淆,尽管“arcsec”可能偶尔混淆于“arcsecond ”。
正如正弦和余弦,反三角函数也依据无穷级数来定义。例如,
arcsin
z
=
z
+
(
1
2
)
z
3
3
+
(
1
⋅
3
2
⋅
4
)
z
5
5
+
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
z
7
7
+
⋯
{\displaystyle \arcsin z=z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots }
这些函数也可以通过证明它们是其他函数的不定积分来定义。例如反正弦函数,可以写为如下积分:
arcsin
(
x
)
=
∫
0
x
1
1
−
z
2
d
z
,
|
x
|
<
1
{\displaystyle \arcsin \left(x\right)=\int _{0}^{x}{\frac {1}{\sqrt {1-z^{2}}}}\,\mathrm {d} z,\quad |x|<1}
可以在反三角函数 条目中找到类似的公式。使用复对数 ,可以把这些函数推广到复辐角上:
arcsin
(
z
)
=
−
i
ln
(
i
z
+
1
−
z
2
)
{\displaystyle \arcsin(z)=-i\ln \left(iz+{\sqrt {1-z^{2}}}\right)}
arccos
(
z
)
=
−
i
ln
(
z
+
z
2
−
1
)
{\displaystyle \arccos(z)=-i\ln \left(z+{\sqrt {z^{2}-1}}\right)}
arctan
(
z
)
=
i
2
ln
(
1
−
i
z
1
+
i
z
)
{\displaystyle \arctan(z)={\frac {i}{2}}\ln \left({\frac {1-iz}{1+iz}}\right)}
三角函数如其名字所暗示的在三角学 中是至关重要的,主要是因为下列两个结果。
正弦定律 三角形 ,它的边是 a , b 和 c 而相对这些边的角是 A , B 和 C ,有:
sin
A
a
=
sin
B
b
=
sin
C
c
{\displaystyle {\frac {\sin A}{a}}={\frac {\sin B}{b}}={\frac {\sin C}{c}}}
也表示为:
a
sin
A
=
b
sin
B
=
c
sin
C
=
2
R
{\displaystyle {\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}=2R}
利萨茹曲线 ,一种三角基的函数形成的图像。它可以通过把三角形分为两个直角三角形并使用正弦的上述定义证明。在这个定理中出现的公共数 (sinA )/a 是通过 A , B 和 C 三点的圆的直径的倒数。正弦定理用于在一个三角形的两个角和一个边已知时计算未知边的长度。这是三角测量 中常见情况。
余弦定律 托勒密定理 的扩展:
c
2
=
a
2
+
b
2
−
2
a
b
cos
C
{\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos C\,}
也表示为:
cos
C
=
a
2
+
b
2
−
c
2
2
a
b
{\displaystyle \cos C={\frac {a^{2}+b^{2}-c^{2}}{2ab}}}
这个定理也可以通过把三角形分为两个直角三角形来证明。余弦定律用于在一个三角形的两个边和一个角已知时确定未知的数据。
如果这个角不包含在这两个边之间,三角形可能不是唯一的(边-边-角全等 歧义)。小心余弦定律的这种歧义情况。
还有一个正切定律
a
+
b
a
−
b
=
tan
[
1
2
(
A
+
B
)
]
tan
[
1
2
(
A
−
B
)
]
{\displaystyle {\frac {a+b}{a-b}}={\frac {\tan[{\frac {1}{2}}(A+B)]}{\tan[{\frac {1}{2}}(A-B)]}}}
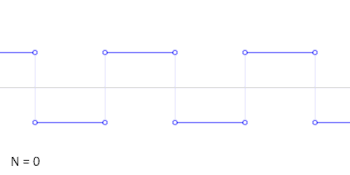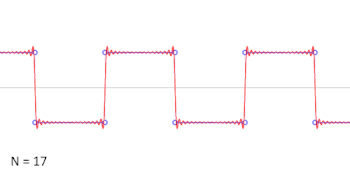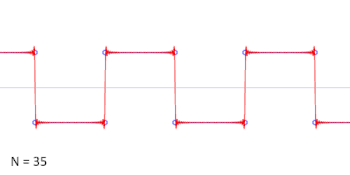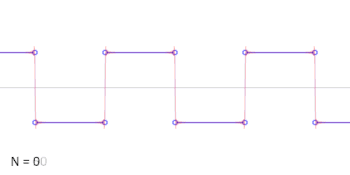
谐波数目递增的方波 的加法合成的动画。 三角函数在物理中也是重要的。例如,正弦和余弦函数被用来描述简单谐波运动 ,它建模了很多自然现象,比如附着在弹簧上的重块的振动,挂在绳子上重块的小角度摆动。正弦和余弦函数是圆周运动 的一维投影。
三角函数还被证明在一般周期函数 的研究中很有用。这些函数有作为图像的特征波模式,对于建模循环现象比如声波或光波是有用的。所有信号都可以写为不同频率的正弦和余弦函数的(典型的无限)和;这是傅立叶分析 的基础想法,这里的三角级数被用来解微分方程的各种边界值问题。例如,方波 可以写为傅立叶级数
x
s
q
u
a
r
e
(
t
)
=
4
π
∑
k
=
1
∞
sin
(
(
2
k
−
1
)
t
)
(
2
k
−
1
)
.
{\displaystyle x_{\mathrm {square} }(t)={\frac {4}{\pi }}\sum _{k=1}^{\infty }{\sin {\left((2k-1)t\right)} \over (2k-1)}.}
在右边的动画中,可以看到只用一些项就已经生成了非常好的逼近。
^ Abramowitz; Weisstein.
^ Needham, p. ix.
^ Kantabutra.
^ However, doing that while maintaining precision is nontrivial, and methods like Gal's accurate tables, Cody and Waite reduction, and Payne and Hanek reduction algorithms can be used.
^ R. P. Brent, "Fast Multiple-Precision Evaluation of Elementary Functions", J. ACM 23 , 242 (1976).
Abramowitz, Milton、Irene A. Stegun,,《Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables》,Dover,New York (1964年),ISBN 0-486-61272-4 。
Boyer, Carl B., 《A History of Mathematics》,John Wiley & Sons, Inc.,第二版(1991年),ISBN 0-471-54397-7 。
Joseph, George G.,《The Crest of the Peacock: Non-European Roots of Mathematics》,第二版,Penguin Books,London,(2000年),ISBN 0-691-00659-8 。
Kantabutra, Vitit,《On hardware for computing exponential and trigonometric functions》,IEEE Trans. Computers 45 (3), 328-339 (1996年)。
Maor, Eli,《Trigonometric Delights》 ,Princeton Univ. Press. (1998年),重印版(2005年2月25日): ISBN 0-691-09541-8 。
Needham, Tristan,《Preface》 ,Visual Complex Analysis ISBN 0-19-853446-9 。
O'Connor, J.J.、E.F. Robertson,《Trigonometric functions》 ,MacTutor History of Mathematics Archive ,(1996年)。
O'Connor, J.J.、E.F. Robertson,《Madhava of Sangamagramma》 , MacTutor History of Mathematics Archive ,(2000年)。
Pearce, Ian G.,《Madhava of Sangamagramma》 ,MacTutor History of Mathematics Archive ,(2002年)。
Weisstein, Eric W.,《Tangent》 ,MathWorld
Template:Link FA
Template:Link FA











































































































































![{\displaystyle {\frac {a+b}{a-b}}={\frac {\tan[{\frac {1}{2}}(A+B)]}{\tan[{\frac {1}{2}}(A-B)]}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/dc3a9eabede6ceceb176a58754cf6557b46f7c3c)
