双射:修订间差异
外观
删除的内容 添加的内容
Add 3 books for verifiability (20211007)) #IABot (v2.0.8.1) (GreenC bot |
|||
| 第64行: | 第64行: | ||
{{refbegin|2}} |
{{refbegin|2}} |
||
* {{cite book|last=Wolf|title=Proof, Logic and Conjecture: A Mathematician's Toolbox|year=1998|publisher=Freeman}} |
* {{cite book|last=Wolf|title=Proof, Logic and Conjecture: A Mathematician's Toolbox|year=1998|publisher=Freeman}} |
||
* {{cite book|last=Sundstrom|title=Mathematical Reasoning: Writing and Proof|year=2003|publisher=Prentice-Hall}} |
* {{cite book|last=Sundstrom|title=Mathematical Reasoning: Writing and Proof|url=https://archive.org/details/mathematicalreas0000sund|year=2003|publisher=Prentice-Hall}} |
||
* {{cite book|last1=Smith|last2=Eggen|last3=St.Andre|title=A Transition to Advanced Mathematics (6th Ed.)|year=2006|publisher=Thomson (Brooks/Cole)}} |
* {{cite book|last1=Smith|last2=Eggen|last3=St.Andre|title=A Transition to Advanced Mathematics (6th Ed.)|year=2006|publisher=Thomson (Brooks/Cole)}} |
||
* {{cite book|last=Schumacher|title=Chapter Zero: Fundamental Notions of Abstract Mathematics|year=1996|publisher=Addison-Wesley}} |
* {{cite book|last=Schumacher|title=Chapter Zero: Fundamental Notions of Abstract Mathematics|year=1996|publisher=Addison-Wesley}} |
||
| 第72行: | 第72行: | ||
* {{cite book|last=Lay|title=Analysis with an introduction to proof|year=2001|publisher=Prentice Hall}} |
* {{cite book|last=Lay|title=Analysis with an introduction to proof|year=2001|publisher=Prentice Hall}} |
||
* {{cite book|last1=Gilbert|last2=Vanstone|title=An Introduction to Mathematical Thinking|year=2005|publisher=Pearson Prentice-Hall}} |
* {{cite book|last1=Gilbert|last2=Vanstone|title=An Introduction to Mathematical Thinking|year=2005|publisher=Pearson Prentice-Hall}} |
||
* {{cite book|last1=Fletcher|last2=Patty|title=Foundations of Higher Mathematics|publisher=PWS-Kent}} |
* {{cite book|last1=Fletcher|last2=Patty|title=Foundations of Higher Mathematics|year=1992|url=https://archive.org/details/foundationsofhig0000flet|publisher=PWS-Kent}} |
||
* {{cite book|last1=Iglewicz|last2=Stoyle|title=An Introduction to Mathematical Reasoning|publisher=MacMillan}} |
* {{cite book|last1=Iglewicz|last2=Stoyle|title=An Introduction to Mathematical Reasoning|publisher=MacMillan}} |
||
* {{cite book|last=Devlin|first=Keith|title=Sets, Functions, and Logic: An Introduction to Abstract Mathematics|year=2004|publisher=Chapman & Hall/ CRC Press}} |
* {{cite book|last=Devlin|first=Keith|title=Sets, Functions, and Logic: An Introduction to Abstract Mathematics|year=2004|publisher=Chapman & Hall/ CRC Press}} |
||
* {{cite book|last1=D'Angelo|last2=West|title=Mathematical Thinking: Problem Solving and Proofs|year=2000|publisher=Prentice Hall}} |
* {{cite book|last1=D'Angelo|last2=West|title=Mathematical Thinking: Problem Solving and Proofs|year=2000|publisher=Prentice Hall}} |
||
* {{cite book|last=Cupillari|title=The Nuts and Bolts of Proofs|publisher=Wadsworth}} |
* {{cite book|last=Cupillari|title=The Nuts and Bolts of Proofs|year=1989|url=https://archive.org/details/nutsboltsofproof00anto|publisher=Wadsworth}} |
||
* {{cite book|last=Bond|title=Introduction to Abstract Mathematics|publisher=Brooks/Cole}} |
* {{cite book|last=Bond|title=Introduction to Abstract Mathematics|publisher=Brooks/Cole}} |
||
* {{cite book|last1=Barnier|last2=Feldman|title=Introduction to Advanced Mathematics|year=2000|publisher=Prentice Hall}} |
* {{cite book|last1=Barnier|last2=Feldman|title=Introduction to Advanced Mathematics|year=2000|publisher=Prentice Hall}} |
||
2021年10月8日 (五) 12:45的版本

| 各種函數 |
|---|
| x ↦ f (x) |
| 不同定義域和陪域 |
| 函數類/性質 |
| 構造 |
| 推廣 |
數學中,一個由集合映射至集合的函數,若對每一在內的,存在唯一一個在內的与其对应,且對每一在內的,存在唯一一個在內的与其对应,則此函數為對射函數。
換句話說,如果其為兩集合間的一一對應,则是雙射的。即,同時為單射和滿射。
例如,由整數集合至的函數,其將每一個整數連結至整數,這是一個雙射函數;再看一個例子,函數,其將每一對實數連結至,這也是個雙射函數。
一雙射函數亦簡稱為雙射(英語:bijection)或置換。後者一般較常使用在時。以由至的所有雙射組成的集合標記為。
雙射函數在許多數學領域扮演著很基本的角色,如在同構的定義(以及如同胚和微分同構等相關概念)、置換群、投影映射及許多其他概念的基本上。
複合函數與反函數
一函數為雙射的若且唯若其逆關係也是個函數。在這情況,也會是雙射函數。
兩個雙射函數及的複合函數亦為雙射函數。其反函數為。
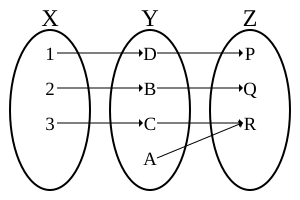
另一方面,若為雙射的,可知是單射的且是滿射的,但也僅限於此。
一由至的關係為雙射函數若且唯若存在另一由至的關係,使得為上的恆等函數,且為上的恆等函數。必然地,此兩個集合會有相同的勢。
雙射與勢
若和為有限集合,則其存在一兩集合的雙射函數若且唯若兩個集合有相同的元素個數。確實,在公理集合論裡,這正是「相同元素個數」的定義,且廣義化至無限集合,並導致了基數的概念,用以分辨無限集合的不同大小。
例子與反例
- 對任一集合,其恆等函數為雙射函數。
- 函數,其形式為,是雙射的,因為對任一,存在一唯一使得。
- 指數函數,其形式為,不是雙射的:因為不存在一內的使得,故非為雙射。但若其陪域改成正實數,則便是雙射的了;其反函數為自然對數函數。
- 函數 : ,其形式為,不是雙射的:因為,故非為雙射。但如果把定義域也改成,則便是雙射的了;其反函數為正平方根函數。
- 不是雙射函數,因為和都在其定義域裡且都映射至。
- 不是雙射函數,因為和2都在其定義域裡且都映射至。
性質
- 一由實數至的函數是雙射的,若且唯若其圖像和任一水平線相交且只相交於一點。
- 設為一集合,則由至其本身的雙射函數,加上其複合函數「」的運算,會形成一個群,即為的對稱群,其標記為、或。
- 取一定義域的子集及一陪域的子集,則
- 且。
- 為一雙射函數。
- 為一滿射函數。
- 為一單射函數。
- 一个严格的单调函数是双射函数,但双射函数不一定是单调函数(例如)。
雙射與範疇論
另見
參考文獻
- Wolf. Proof, Logic and Conjecture: A Mathematician's Toolbox. Freeman. 1998.
- Sundstrom. Mathematical Reasoning: Writing and Proof. Prentice-Hall. 2003.
- Smith; Eggen; St.Andre. A Transition to Advanced Mathematics (6th Ed.). Thomson (Brooks/Cole). 2006.
- Schumacher. Chapter Zero: Fundamental Notions of Abstract Mathematics. Addison-Wesley. 1996.
- O'Leary. The Structure of Proof: With Logic and Set Theory. Prentice-Hall. 2003.
- Morash. Bridge to Abstract Mathematics. Random House.
- Maddox. Mathematical Thinking and Writing. Harcourt/ Academic Press. 2002.
- Lay. Analysis with an introduction to proof. Prentice Hall. 2001.
- Gilbert; Vanstone. An Introduction to Mathematical Thinking. Pearson Prentice-Hall. 2005.
- Fletcher; Patty. Foundations of Higher Mathematics. PWS-Kent. 1992.
- Iglewicz; Stoyle. An Introduction to Mathematical Reasoning. MacMillan.
- Devlin, Keith. Sets, Functions, and Logic: An Introduction to Abstract Mathematics. Chapman & Hall/ CRC Press. 2004.
- D'Angelo; West. Mathematical Thinking: Problem Solving and Proofs. Prentice Hall. 2000.
- Cupillari. The Nuts and Bolts of Proofs. Wadsworth. 1989.
- Bond. Introduction to Abstract Mathematics. Brooks/Cole.
- Barnier; Feldman. Introduction to Advanced Mathematics. Prentice Hall. 2000.
- Ash. A Primer of Abstract Mathematics. MAA.
外部連結
维基共享资源中相关的多媒体资源:Bijectivity














































![{\displaystyle \mathbb {R} \to [-1,1]:x\mapsto \sin(x)}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/dbb23cd8a0d8771ac197194b8610e7451013d752)












