1A2B：修订间差异
回退到InternetArchiveBot在2022-01-14 07:30:23時製作的修訂版本69650811，透過popups 标签：手工回退 |
原文對人工智慧的意思誤解 |
||
| 第15行： | 第15行： | ||
| footnotes = |
| footnotes = |
||
}} |
}} |
||
'''猜數字'''是一种[[益智游戏]]，遊戲人數為兩人，或一人與一個 |
'''猜數字'''是一种[[益智游戏]]，遊戲人數為兩人，或一人與一個運算機器。 |
||
==玩法== |
==玩法== |
||
2022年2月20日 (日) 16:59的版本
此條目介紹的是和數字位置有關的益智游戏。关于根據猜測數字太大或太小而進行的益智游戏，请见「終極密碼」。 | 此條目可能包含原创研究。 (2019年1月31日) |
 | 此條目需要补充更多来源。 (2019年1月31日) |
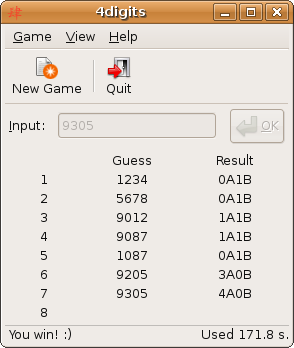 4digits的運行畫面 | |
| 玩家數目 | 2人 |
|---|---|
| 複雜程度 | 低 |
| 所需技巧 | 分析 |
猜數字是一种益智游戏，遊戲人數為兩人，或一人與一個運算機器。
玩法
一個人設定一組四碼的数字作為謎底，另一方猜。每猜一个数，出数者就要根据这个数字给出提示，提示以XAYB形式呈現，直到猜中為止。其中X表示位置正确的数的个数，而Y表示数字正确而位置不对的数的个数。
例如，當謎底為8123，而猜謎者猜1052時，出題者必須提示0A2B。
例如，當謎底為5637，而猜謎者猜4931時，出題者必須提示1A0B。
含重复数字的猜数字
有一种使用范围比较狭窄的猜数字，是允许重复数字存在的猜数字，但由于其规则较复杂，故没有得到广泛的推广。其规则如下：
除了上面的规则外，如果有出现重复的数字，则重复的数字每个也只能算一次，且以最优的结果为准，
如正确答案为5543，猜的人猜5255，则在这里不能认为猜测的第一个5对正确答案第二个，根据最优结果为准的原理和每个数字只能有一次的规则，两个比较后应该为1A1B，第一个5位置正确，记为1A；猜测数字中的第三个5或第四个5和答案的第二个5匹配，只能记为1B。当然，如果有猜5267中的第一个5不能与答案中的第二个5匹配，因此只能记作1A0B。
解法
對於第一種玩法而言，有以下的解法：
计算机解
通常采用的计算机解是通过排除法，即遍历所有可能的数，将不符合要求的数剃掉。[1]
下面是一个计算机处理的例子：
for (int i = 0; i < Array.Count; i++)
{
if (请求提示(Array[i]) == 全A)
return Array[i];
}
这个代码采用C#的语法，其中Array表示所有可能的数字的集合。这个例子为了方便说明，结合了语言的描述。
这样的方法充分利用了计算机计算速度快的优势，使用穷举法，并不进行推理。数字越长猜测时间越长。
推理解
计算机解是根据这种方法推广的。这种解法的中心思想是假设猜的这个数字是正确答案，即如果它为正确答案，那么这个数应该符合已经猜测的数及其结果。如已经有
1234 0A0B
那么下一步就不能猜含有1234中任一数字的数，因为如果正确答案含1234中任一數字；則出題者不會說1234是0A0B。
再假設如果出題者說 5678 是 0A1B 的話，則正確答案必須只包含5、6、7、8其中僅僅一個數字，且如果有5、6、7、8的話，5的位置必須不在(左邊數起)第一個位置、6的位置必須不在(左邊數起)第二個位置、7的位置必須不在(左邊數起)第三個位置、8的位置必須不在(左邊數起)第四個位置。
再假設如果出題者說 1357 是 1A0B 的話，則正確答案必須只包含1、3、5、7其中僅僅一個數字，且如果有1、3、5、7的話，1的位置必須在(左邊數起)第一個位置、3的位置必須在(左邊數起)第二個位置、5的位置必須在(左邊數起)第三個位置、7的位置必須在(左邊數起)第四個位置。
基于这个解法，根据个人思维风格和起始数字选择的不同，以及对出题者出数风格的猜测，經過一些計算機程式的大量模擬，猜到答案的平均次數大約為5.3次。顯然地，如果運氣夠好，有機會可以在一次、兩次猜到答案；運氣不好之時，花費八次猜測才找到答案也不無可能。
使用这种解法需要考虑的时间很久，不是很適合人們使用；特別是在限時賽中，人們很難檢視所有可能的候選答案，然後選擇其中最佳者。事實上，有興趣的數學研究者，提出一種證明方法，證明了四位數(數字不重複、零可以開頭)的猜數字遊戲，在最佳狀況下，可以用至多七次的猜測找到對手的答案，而平均來說，只要花5.2131次的猜測來完成一次的遊戲。[2][3]
代入解
即在推理出不可能的數字後，將餘下可能的數字依序帶入。
參考資料
- ^ 電腦(1A2B)猜數字遊戲的策略. 陳麒全、林新富、陳鴻宜. [2021-08-20]. （原始内容存档于2021-08-20）.
- ^ Optimal algorithms for bulls and cows game. (PDF). [2012-08-17]. （原始内容存档 (PDF)于2013-05-20）.
- ^ http://www.cs.nccu.edu.tw/~chaolin/papers/science3203.pdf （页面存档备份，存于互联网档案馆） 劉昭麟. 數學、資訊科學與數字遊戲, 科學月刊，第32卷第3期，第250到255頁， 財團法人臺北市科學出版事業基金會,2001.
其他
著名的桌上遊戲Master Mind （页面存档备份，存于互联网档案馆）（珠機妙算），就是這種遊戲形式的實物道具版本，只是把所要猜的由數字改為顏色。
