擬詹森多面體：修订间差异

删除的内容添加的内容

行内

2023年2月1日 (三) 14:07的版本

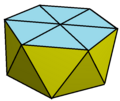
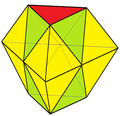
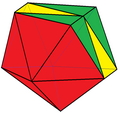
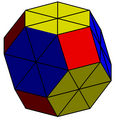
在幾何學中，擬詹森多面體是嚴格凸多面體，其面幾乎都是正多邊形，但其中有部分或全部的面不是正多邊形但很接近正多邊形。這種多面體也包含詹森多面體，即所有的面都是正多邊形，而擬詹森多面體經常會在正多邊形與非正多邊形之間有物理構造上可以忽略的微小差異^[1]。近似的精確值取決於這樣一個多面體的面逼近正多邊形的程度。

例子

名稱康威多面體表示法	頂點布局（英语：Vertex configuration）	頂點	邊	面	F₃	F₄	F₅	F₆	F₁₀	F₁₂	對稱性（英语：List of spherical symmetry groups）
底面截角雙三角錐 t4dP3	2 (5.5.5) 12 (4.5.5)	14	21	9		3	6				Dih₃ order 12
截角三角化四面體 t6kT	4 (5.5.5) 24 (5.5.6)	28	42	16			12	4			T_d, [3,3] order 24
五邊形六邊形五角十二面七十四面體	12 (3.5.3.6) 24 (3.3.5.6) 24 (3.3.3.3.5)	60	132	74	56		12	6			T_h, [3⁺,4] order 24
倒角立方體 cC	24 (4.6.6) 8 (6.6.6)	32	48	18		6		12			O_h, [4,3] order 48
--	12 (5.5.6) 6 (3.5.3.5) 12 (3.3.5.5)	30	54	26	12		12	2			D_6h, [6,2] order 24
--	6 (5.5.5) 9 (3.5.3.5) 12 (3.3.5.5)	27	51	26	14		12				D_3h, [3,2] order 12
四階十二面體	4 (5.5.5) 12 (3.5.3.5) 12 (3.3.5.5)	28	54	28	16		12				T_d, [3,3] order 24
部分截半截角八面體	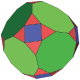24 (3.4.3.9) 24 (3.9.9)	38	84	48	24	6					O_h, [4,3]
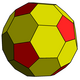
倒角十二面體 cD	60 (5.6.6) 20 (6.6.6)	80	120	42			12	30			I_h, [5,3] order 120
截半截角二十面體 atI	60 (3.5.3.6) 30 (3.6.3.6)	90	180	92	60		12	20			I_h, [5,3] order 120
截角截角二十面體 ttI	120 (3.10.12) 60 (3.12.12)	180	270	92	60				12	20	I_h, [5,3] order 120
擴展截角二十面體 etI	60 (3.4.5.4) 120 (3.4.6.4)	180	360	182	60	90	12	20			I_h, [5,3] order 120
扭稜截角二十面體 stI	60 (3.3.3.3.5) 120 (3.3.3.3.6)	180	450	272	240		12	20			I, [5,3]⁺ order 60

共面擬詹森多面體

有些未能成為詹森多面體的候選多面體是因為其存在有兩個以上共面的面，其也可以算是全部由正多邊形組成的凸多面體，只是其凸為非嚴格凸。^[2]這些多面體可被看做是凸的面且非常接近正多邊形。這些立體通常有無限多種，但若約定所有頂點要位於頂角處，不能位於面（共面的一組面視為同一個面）的內部，則滿足條件的立體只有78個，可以視為詹森多面體的自然推廣^[2]（參見章節條件邊正多邊形凸多面體）。

例如： 3.3...：

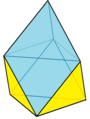
同相雙三角柱
（菱形柱）
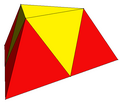
楔形體
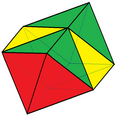
二側錐八面體
（三方偏方面體）
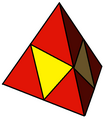
正三角錐反角柱
間三側錐八面體
長八面體
間四側錐八面體
正六角錐反角柱
（正六角反棱柱）
邊收縮二十面體
 十八面體
四側錐截角四面體
（截角四面體）
八側錐截角八面體
（截角八面體）
雙六角錐柱
（六角柱）
正三角帳塔錐
（正三角帳塔）

4.4.4.4：

正方形二十四面體
（正方體）

3.4.6.4：

正六角帳塔
（退化）

條件邊正多邊形凸多面體

若將詹森多面體的條件放寬成允許面兩兩共面，且所有頂點都要嚴格位於頂角上，不能有邊兩兩共線的情況（若允許邊兩兩共線，則結果會有無窮多種情況），也不能夠有頂點位於共面區域內部的情況，則能夠再列出有限個有此特性的立體。條件邊指的是對應棱的二面角為平角的邊。^[2]在這條件下，能允許互相共面的面有正三角形與正三角形（3+3）、正三角形與正方形（3+4）、正三角形與正五邊形（3+5）、正方形和兩個位於對側的正三角形（3+4+3）、正五邊形和兩個不相鄰的正三角形（3+5+3），也就是說，這些立體除了有正多邊形面外，也會存在上述組合之形狀的面。^[3]這類立體一共有78個。^[2]和詹森多面體一樣，這些立體除了一些基本立體外，都能夠用柱體、錐體和28種立體互相組合而成。^[3]亞歷克斯·多斯基（Alex Doskey）^[4]、羅傑·考夫曼（Roger Kaufman）和史蒂夫·沃特曼（Steve Waterman）^[5]在2006年列出了大部分有此性質的立體。2008年，維克多·扎加勒（Victor Zalgaller）^[6]和阿列克謝·維克多羅維奇·蒂莫芬科（Aleksei Victorovich Timofeenko）^[7]獨立發現並列出這些立體。2010年，蒂莫芬科證明這些立體只有78種。^[7]^[8]

P_n,k^[7]	S_n^[6]	名稱	組合	頂點	邊	面	F₃	F₄	F₅	F₆	F₈	F₁₀	F₃₊₃	F_etc
Q₁	Q₁	斜六角柱	（基本立體）	12	18	8		2		2			4
Q₂	Q₂	六斜方十二面體（hexarhombic dodecahedron）	（基本立體）	18	28	12		4		4			4
Q₃	Q₃	（未命名）	（基本立體）	15	29	16	9	2	3				2
Q₄	Q₄	（未命名）	（基本立體）	15	27	14	5	2	3				4
Q₅	Q₅	（未命名）	（基本立體）	22	42	22	10	4	2	2			4
Q₆	Q₆	（未命名）	（基本立體）	18	33	17	7	3	3	1			3
P_2,2	S₃	同相雙三角柱	三角柱	8	12	6		4					2
P_2,3	S₄	側三角柱立方體	三角柱+立方體	10	15	7		5						2
P_2,4	S₅	側三角柱五角柱	三角柱+五角柱	12	18	8		6						2
P_2,22	S₁₄	側錐四角錐	正四面體+四角錐	6	9	5	2	1					2
P_2,25	S₁₇	側錐三角台塔	三角台塔+四角錐	10	16	8	2	2		1			3
P_2,29	S₂₂	側錐雙新月雙罩帳	雙新月雙罩帳+五角錐	15	29	16	9	2	3				2
P_2,30	S₄₆	側錐五角丸塔	五角丸塔+五角錐	21	36	17	7		5			1	4
P_2,31	S₂₄	五角丸塔錐	五角丸塔+五角錐	21	35	16	5		5			1	5
P_2,33	S₂	側錐三角廣底球狀罩帳	三角廣底球狀罩帳+五角錐	19	38	21	12	3	2	1			3
P_2,34	S₁	異側鄰二側錐雙新月雙罩帳	雙新月雙罩帳+五角錐	16	32	18	10	2	2				4
P_2,38	S₅₉	單旋側台塔截角四面體	截角四面體+三角台塔	15	24	11	2	3		3			3
P_2,42	S₆₀	單旋側台塔截角立方體	截角立方體+四角台塔	28	44	18	4	5			5		4
P_2,48	S₆₃	單旋側台塔截角十二面体	截角十二面体+五角台塔	65	100	37	15	5	1			11	5
P_3,1	S₆	側錐同相雙三角柱	三角柱+四角錐	9	16	9	4	3					2
P_3,2	S₁₀	柱化異相雙三角柱	三角柱+立方體	12	18	8		4						4
P_3,3	S₁₁	柱化同相雙三角柱	三角柱+立方體	12	18	8		6						2
P_3,4	S₉	對側錐側三角柱立方體	三角柱+立方體+四角錐	11	19	10	4	4						2
P_3,5	S₁₂	間二側三角柱五角柱	三角柱+五角柱	14	21	9		7						2
P_3,6	S₁₃	間側錐側三角柱五角柱	三角柱+五角柱+四角錐	13	22	11	4	5						2
P_3,22	S₄₀	五角丸塔錐柱	五角丸塔+十角柱+五角錐	31	55	26	5	10	5			1	5
P_3,31	S₄₁	五角丸塔錐反棱柱	五角丸塔+五角反棱柱+五角錐	31	65	36	25		5			1	5
P_3,33	S₁₅	側錐八面體	正八面體+正四面體	7	12	7	4						3
P_3,34	S₁₈	側錐同相雙三角台塔	三角台塔+四角錐	13	25	14	6	5					3
P_3,35	S₂₀	側錐截半立方體	截半立方體+四角錐	13	24	13	4	5					4
P_3,36	S₂₃	對二側錐雙新月雙罩帳	雙新月雙罩帳+五角錐	16	32	18	10	2	2				4
P_3,37	S₄₇	間二側錐五角丸塔	五角丸塔+五角錐	22	37	17	4		4			1	8
P_3,38	S₄₈	罩帳側錐異相五角帳塔罩帳	五角丸塔+五角台塔+五角錐	26	51	27	12	5	6				4
P_3,39	S₄₉	罩帳側錐同相五角帳塔罩帳	五角丸塔+五角台塔+五角錐	26	51	27	12	5	6				4
P_3,40	S₂₇	側錐截半二十面体	截半二十面体+五角錐	31	60	31	15		11				5
P_3,41	S₅₂	側錐同相雙五角丸塔	同相雙五角罩帳（英语：Pentagonal orthobirotunda）+五角錐	31	61	32	17		11				4
P_3,42	S₂₅	異相五角帳塔罩帳錐	五角帳塔+五角罩帳+五角錐	26	50	26	10	5	6				5
P_3,43	S₂₆	同相五角帳塔罩帳錐	五角帳塔+五角罩帳+五角錐	26	50	26	10	5	6				5
P_3,44	S₂₈	同相雙五角罩帳錐	五角罩帳+五角錐	31	60	31	15		11				5
P_3,48	S₆₁	單旋二側台塔截角立方體	截角立方體+四角台塔	32	56	26	8	10			4		4
P_3,49	S₆₂	雙旋二側台塔截角立方體	截角立方體+四角台塔	32	52	22		10			4		8
P_3,51	S₆₆	單旋間二側台塔截角十二面体	截角十二面体+五角台塔	70	115	47	20	10	2			10	5
P_3,53	S₆₄	單旋對二側台塔截角十二面体	截角十二面体+五角台塔	70	115	47	20	10	2			10	5
P_3,54	S₆₇	雙旋間二側台塔截角十二面体	截角十二面体+五角台塔	70	110	42	10	10	2			10	10
P_3,55	S₆₅	雙旋對二側台塔截角十二面体	截角十二面体+五角台塔	70	110	42	10	10	2			10	10
P_4,1	S₇	鄰二側錐同相雙三角柱	三角柱+四角錐	10	20	12	8	2					2
P_4,2	S₈	對二側錐同相雙三角柱	三角柱+四角錐	10	20	12	8	2					2
P_4,5	S₃₁	同相五角台塔丸塔柱錐	五角台塔+五角丸塔+十角柱+五角錐	36	70	36	10	15	6				5
P_4,6	S₃₂	異相五角台塔丸塔柱錐	五角台塔+五角丸塔+十角柱+五角錐	36	70	36	10	15	6				5
P_4,7	S₃₃	同相雙五角丸塔柱錐	五角丸塔+十角柱+五角錐	41	80	41	15	10	11				5
P_4,8	S₃₄	異相雙五角丸塔柱錐	五角丸塔+十角柱+五角錐	41	80	41	15	10	11				5
P_4,9	S₃₇	五角台塔丸塔反棱柱錐	五角台塔+五角丸塔+十角反棱柱+五角錐	36	80	46	30	5	6				5
P_4,10	S₃₈	雙五角丸塔反棱柱錐	五角丸塔+十角反棱柱+五角錐	41	90	51	35		11				5
P_4,11	S₁₆	二側錐八面體	正四面體+正八面體	8	12	6							6
P_4,12	S₁₉	間二側錐同相雙三角台塔	三角台塔+四角錐	14	26	14	4	4					6
P_4,13	S₂₁	對二側錐截半立方體	截半立方體+四角錐	14	24	12		4					8
P_4,14	S₅₀	間二側錐異相五角帳塔罩帳	五角帳塔+五角罩帳+五角錐	27	52	27	9	5	5				8
P_4,15	S₅₁	間二側錐同相五角帳塔罩帳	五角帳塔+五角罩帳+五角錐	27	52	27	9	5	5				8
P_4,16	S₄₄	間二側錐截半二十面体	截半二十面体+五角錐	32	60	30	10		10				10
P_4,17	S₅₃	同側間二側錐同相雙五角罩帳	五角罩帳+五角錐	32	62	32	14		10				8
P_4,18	S₂₉	對二側錐截半二十面体	截半二十面体+五角錐	32	60	30	10		10				10
P_4,19	S₅₇	異側鄰二側錐同相雙五角罩帳	五角罩帳+五角錐	32	62	32	14		10				8
P_4,20	S₅₈	異側對二側錐同相雙五角罩帳	五角罩帳+五角錐	32	62	32	14		10				8
P_4,21	S₄₂	異側側錐同相雙五角罩帳錐	五角罩帳+五角錐	32	61	31	12		10				9
P_4,22	S₃₀	同相雙五角罩帳雙錐	五角罩帳+五角錐	32	60	30	10		10				10
P_4,25	S₆₈	單旋三側帳塔截角十二面體	截角十二面体+五角帳塔	75	130	57	25	15	3			9	5
P_4,26	S₆₉	雙旋三側帳塔截角十二面體	截角十二面体+五角帳塔	75	125	52	15	15	3			9	10
P_4,27	S₇₀	三旋三側帳塔截角十二面體	截角十二面体+五角帳塔	75	120	47	5	15	3			9	15
P_4,30		斜四角柱	正四面體+四角錐	8	12	6		2					4
P_4,31		雙重側錐四角錐（doubled augmented square pyramid）雙斜三角柱（doubled oblique triangular prism）扭斜四角柱（twist slant square prism）	正四面體+四角錐	8	14	8	4	2					2
P_5,1	S₃₅	同相雙五角罩帳柱雙錐	五角罩帳+十角柱+五角錐	42	80	40	10	10	10				10
P_5,2	S₃₆	異相雙五角罩帳柱雙錐	五角罩帳+十角柱+五角錐	42	80	40	10	10	10				10
P_5,3	S₃₉	雙五角罩帳反棱柱雙錐	五角罩帳+十角反棱柱+五角錐	42	90	50	30		10				10
P_5,4	S₄₅	三側錐截半二十面体	截半二十面体+五角錐	33	60	29	5		9				15
P_5,5	S₅₅	異側連三側錐同相雙五角罩帳	五角罩帳+五角錐	33	63	32	11		9				12
P_5,6	S₅₆	異側偏三側錐同相雙五角罩帳	五角罩帳+五角錐	33	63	32	11		9				12
P_5,7	S₄₃	異側間二側錐同相雙五角罩帳錐	五角罩帳+五角錐	33	62	31	9		9				13
P_6,1	S₅₄	四側錐同相雙五角罩帳錐	五角罩帳+五角錐	34	64	32	8		8				16

參見

參考文獻

^ Kaplan, Craig S.; Hart, George W., Symmetrohedra: Polyhedra from Symmetric Placement of Regular Polygons, Bridges: Mathematical Connections in Art, Music and Science (PDF), 2001 [2014-05-01], （原始内容存档 (PDF)于2015-09-23） .
^ ^2.0 ^2.1 ^2.2 ^2.3 Robert R Tupelo-Schneck. Convex regular-faced polyhedra with conditional edges.
^ ^3.0 ^3.1 Robert R Tupelo-Schneck. Regular-faced Polyhedra.
^ Alex Doskey. Convex Diamond-Regular Polyhedra.
^ Steve Waterman. Convex hulls having regular diamonds.
^ ^6.0 ^6.1 Gurin, AM and Zalgaller, VA. On the history of the study of convex polyhedra with regular faces and faces composed of regular ones. Translations of the American Mathematical Society-Series 2. 2009, 228: 169.
^ ^7.0 ^7.1 ^7.2 Timofeenko, Aleksei Victorovich. Junction of noncomposite polygons. Algebra i Analiz (St. Petersburg Department of Steklov Institute of Mathematics, Russian~…). 2009, 21 (3): 165–209.
^ Timofeenko, Aleksei Victorovich. Corrections to “Junction of noncomposite polyhedra”. St. Petersburg Mathematical Journal. 2012-08-01, 23 (4): 779–780 [2023-01-31]. ISSN 1061-0022. doi:10.1090/S1061-0022-2012-01217-3 （英语）.

Near Misses （页面存档备份，存于互联网档案馆）
24 Johnson Solid Near Misses （页面存档备份，存于互联网档案馆）

[1] Kaplan, Craig S.; Hart, George W., Symmetrohedra: Polyhedra from Symmetric Placement of Regular Polygons, Bridges: Mathematical Connections in Art, Music and Science (PDF), 2001 [2014-05-01], （原始内容存档 (PDF)于2015-09-23） .

[Robert_R_Tupelo-Schneck_conditional_edges-2] 2.0 ^2.1 ^2.2 ^2.3 Robert R Tupelo-Schneck. Convex regular-faced polyhedra with conditional edges.

[Robert_R_Tupelo-Schneck_Regular-faced_Polyhedra-3] 3.0 ^3.1 Robert R Tupelo-Schneck. Regular-faced Polyhedra.

[4] Alex Doskey. Convex Diamond-Regular Polyhedra.

[5] Steve Waterman. Convex hulls having regular diamonds.

[article_gurin2009history-6] 6.0 ^6.1 Gurin, AM and Zalgaller, VA. On the history of the study of convex polyhedra with regular faces and faces composed of regular ones. Translations of the American Mathematical Society-Series 2. 2009, 228: 169.

[article_timofeenko2009junction-7] 7.0 ^7.1 ^7.2 Timofeenko, Aleksei Victorovich. Junction of noncomposite polygons. Algebra i Analiz (St. Petersburg Department of Steklov Institute of Mathematics, Russian~…). 2009, 21 (3): 165–209.

[A._V._Timofeenko_2012-8] Timofeenko, Aleksei Victorovich. Corrections to “Junction of noncomposite polyhedra”. St. Petersburg Mathematical Journal. 2012-08-01, 23 (4): 779–780 [2023-01-31]. ISSN 1061-0022. doi:10.1090/S1061-0022-2012-01217-3 （英语）.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

@@ 第242行： / 第242行： @@
   |pages=165-209
   |year=2009
-  |publisher=St. Petersburg Department of Steklov Institute of Mathematics, Russian~…}}</ref>獨立發現並列出這些立體。2010年，蒂莫芬科證明這些立體只有78種。<ref name="A. V. Timofeenko 2012">{{cite journal|journal=St. Petersburg Mathematical Journal|volume=23|issue=4|language=en|issn=1061-0022|date=2012-08-01|pages=779–780|doi=10.1090/S1061-0022-2012-01217-3|url=http://www.ams.org/jourcgi/jour-getitem?pii=S1061-0022-2012-01217-3|title=Corrections to “Junction of noncomposite polyhedra”|accessdate=2023-01-31|author=Timofeenko, Aleksei Victorovich}}</ref>
+  |publisher=St. Petersburg Department of Steklov Institute of Mathematics, Russian~…}}</ref>獨立發現並列出這些立體。2010年，蒂莫芬科證明這些立體只有78種。<ref name= "article timofeenko2009junction"/><ref name="A. V. Timofeenko 2012">{{cite journal|journal=St. Petersburg Mathematical Journal|volume=23|issue=4|language=en|issn=1061-0022|date=2012-08-01|pages=779–780|doi=10.1090/S1061-0022-2012-01217-3|url=http://www.ams.org/jourcgi/jour-getitem?pii=S1061-0022-2012-01217-3|title=Corrections to “Junction of noncomposite polyhedra”|accessdate=2023-01-31|author=Timofeenko, Aleksei Victorovich}}</ref>
 {| class="wikitable sortable"
-!P<sub>n,k</sub><ref name="A. V. Timofeenko 2012"/>
+!P<sub>n,k</sub><ref name= "article timofeenko2009junction"/>
 !S<sub>n</sub><ref name=" article gurin2009history"/>
 !名稱

查论编擬詹森多面體
種類	面近似正多邊形條件邊正多邊形凸多面體共面擬詹森多面體
截角形式	截角三角化四面體倒角立方体 (截角菱形十二面體) 倒角十二面體 (截角菱形三十面體)
不完全變換形式	部分截半截角八面體部分截角截四階角五角二十四面體
其他形式	四階十二面體截半截角二十面體五邊形六邊形五角十二面七十四面體