叉积
此條目没有列出任何参考或来源。 (2017年2月13日) |
叉積(英語:Cross product)是一种在向量空间中向量的二元运算。与点积不同,它的运算结果是一个向量而不是一个标量。两个向量的叉积写作,也称作外积(英語:Outer product)或向量积(英語:Vector product)。叉积与原来的两个向量都垂直。
定义

两个向量和的叉积写作 (有时也被写成,避免和字母x混淆)。叉积可以定义为:
在这里表示和之间的角度(),它位于这两个向量所定义的平面上。而是一个与、所构成的平面垂直的单位向量。
这个定义有个问题,就是同时有两个单位向量都垂直于和:若满足垂直的条件,那么也满足。
“正确”的向量由向量空间的方向确定,即按照给定直角坐标系的左右手定则。若(、、)满足右手定则,则(、、)也满足右手定则;或者两者同时满足左手定则。
一个简单的确定满足“右手定则”的结果向量的方向的方法是这样的:若坐标系满足右手定则,当右手的四指从以不超过180°的转角转向时,竖起的大拇指指向是的方向。由于向量的叉积由坐标系确定,所以其结果被称为「伪向量」。
性质
代数性质
對於任意三個向量、、,
一般來說,向量叉積不遵守約簡律,即不表示。此外,不表示或。
但對於两个非零向量和,
- 當且僅當平行於
三重積
純量三重積满足以下特殊的结合律:
向量三重積不满足结合律,但满足以下恆等式:
- (雅可比恆等式)
向量三重積亦可以點積展開:
- (拉格朗日公式)
向量微分
對於實數和兩個向量值函數、,乘積法則成立:
三維坐標
给定直角坐标系的单位向量,,满足下列等式:
- 、、
通过这些规则,两个向量的叉积的坐标可以方便地计算出来,不需要考虑任何角度:设
则
叉积也可以用四元数来表示。注意到上述、、之间的叉积满足四元数的乘法。一般而言,若将向量[a1, a2, a3]表示成四元数a1i + a2j + a3k,两个向量的叉积可以这样计算:计算两个四元数的乘积得到一个四元数,并将这个四元数的实部去掉,即为结果。更多关于四元数乘法,向量运算及其几何意义请参见四元数与空间旋转。
几何意义
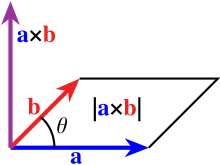
由向量和定義兩條鄰邊的平行四边形,其面積為
因此兩支向量叉積的模長可視作平行四边形其面積:
高维情形
七维向量的叉积可以通过八元数得到,与上述的四元数方法相同。
七维叉积具有与三维叉积相似的性质:
- 双线性性:
- 反交换律:
- 同时与和垂直:
- 不同于三维情形,它并不满足雅可比恒等式:
应用
另外,在物理学力学、电磁学、光学和计算机图形学等理工学科中,叉积应用十分广泛。例如力矩、角动量、洛伦兹力等矢量都可以由向量的叉积求解。在进行这些物理量的计算时,往往可以借助右手定则辅助判断方向。





















































