不連續點

不連續點是指：在非連續函數y=f(x)中某點處x_o處有中斷現象，那麼，x_o就稱為函數的不連續點。

分類

根據不同不連續點的性質，通常把不連續點分為兩類：

1. 第一類不連續點：
   1. 跳躍不連續點：不連續點兩側函數的極限存在，但不相等；
   2. 可去不連續點：不連續點兩側函數的極限存在且相等。
2. 第二類不連續點：

不屬於第一類不連續點的任何一種不連續點都屬於第二類不連續點。

外部連結

• YAN Kun. Adaptive connection equation in discontinuous area of data curve. DOI:10.3969/j.issn.1004-2903.2011.01.018

例子

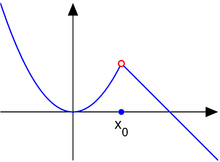可去不連續點

1. 考慮以下函數：

$f(x)={\begin{cases}x^{2}&{\mbox{ for }}x<1\\0&{\mbox{ for }}x=1\\2-x&{\mbox{ for }}x>1\end{cases}}$

點$x_{0}=1$是可去不連續點。

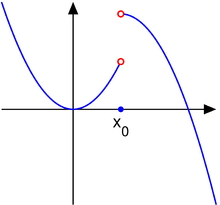跳躍不連續點

2. 考慮以下函數：

$f(x)={\begin{cases}x^{2}&{\mbox{ for }}x<1\\0&{\mbox{ for }}x=1\\2-(x-1)^{2}&{\mbox{ for }}x>1\end{cases}}$

點$x_{0}=1$是跳躍不連續點。

第二類不連續點

3. 考慮以下函數：

$f(x)={\begin{cases}\sin {\frac {5}{x-1}}&{\mbox{ for }}x<1\\0&{\mbox{ for }}x=1\\{\frac {0.1}{x-1}}&{\mbox{ for }}x>1\end{cases}}$

點$x_{0}=1$是第二類不連續點，又稱本性不連續點。