User:JC1/twenty-second

光速

太陽光平均只要8分19秒即可到達地球。
準確數字
米每秒	7008299792458000000♠299792458
普朗克	1
大約數字
公里每秒	300,000
公里每小時	1,080,000,000
英里每秒	186,000
英里每小時	671,000,000
天文單位每日	173
前進某一距離所需時間
距離	時間
1英尺	1.0納秒
1米	3.3納秒
從地球靜止軌道到地面	119毫秒
赤道長度	134毫秒
從月球到地球	1.3秒
從太陽到地球（1天文單位）	8.3分鐘
從毗鄰星到太陽（1.3秒差距）	4.2年
從大犬座矮星系到地球	25,000年
橫越銀河系	100,000年
從仙女座星系到地球	2,500,000年

光速，通常指光波傳播的速度。光在真空中傳播的速度，又名${\begin{smallmatrix}c\end{smallmatrix}}$，是一個於物理學中極為重要的物理常數。此值為299,792,458米每秒。其為一實數，因為秒為國際單位，而米的長度亦由光速定義。以英制單位來說，此值約為186,282尺每秒。

跟據狹義相對論，${\begin{smallmatrix}c\end{smallmatrix}}$是宇宙中所有能量、物質或資訊所能達至的最高速度。${\begin{smallmatrix}c\end{smallmatrix}}$也是無質量粒子及相關的場（包括電磁波，如光）於真空中前進的速度。其亦是現時理論中預測重力波的傳遞速度。上述的粒子或波皆以${\begin{smallmatrix}c\end{smallmatrix}}$傳遞，不論來源有否運動或觀察者的慣性參考系。相對論中，${\begin{smallmatrix}c\end{smallmatrix}}$與時空相關連，亦出現於質能等價公式${\begin{smallmatrix}E=mc^{2}\end{smallmatrix}}$之中。

光線傳播時若通過透明的物質，如空氣或水，則其速度會低於${\begin{smallmatrix}c\end{smallmatrix}}$，而該速度${\begin{smallmatrix}v\end{smallmatrix}}$與${\begin{smallmatrix}c\end{smallmatrix}}$的比例為折射率－${\begin{smallmatrix}n\end{smallmatrix}}$（${\begin{smallmatrix}n={\tfrac {c}{v}}\end{smallmatrix}}$）。例如可見光於玻璃的折射率通常約為1.5，即光於玻璃中傳播時的速度為${\begin{smallmatrix}{\tfrac {c}{1.5}}\thickapprox 200,000\end{smallmatrix}}$ 公里每秒；空氣的折射率約為1.0003，即光於空氣中的速度比${\begin{smallmatrix}c\end{smallmatrix}}$慢約90公里每秒。

大部分情況下，光都可以被理解為「瞬間到達」，但當距離較長或要求非常精準時光的速度就顯得非常重要。當與遙遠的太空探測器溝通時，其需要數分鐘甚至以小時計來傳遞訊息。由於星系之間的距離極長，所以我們看到的星光實際上由恆星於很多年前發出，使我們能借此研究宇宙的歷史。光線有限的速度也限制了電腦於理論上的最高速度，因為電腦中的信息需於集成電路之間傳遞。最後，光速亦能用於精確測量長距離的飛行。

奧勒·羅默於1676年首次以木衛一與木星之間的掩食演示了光的速度有限。1865年，詹姆斯·克拉克·馬克士威提出光是一種電磁波，因此在他的理論中為光速予以${\begin{smallmatrix}c\end{smallmatrix}}$。1905年，阿爾伯特·愛因斯坦假設光速對於任何慣性系來說都是獨立於其光源，並根據狹義相對論探討了一些推論，並由此顯示${\begin{smallmatrix}c\end{smallmatrix}}$不只在光和電磁方面的相關性。經過百多年來越來越精確的測量，1975年測出為約為7008299792458000000♠299792458米每秒。1983年，國際單位制將米按光速重新定義，改為每秒的299,792,458分之1。

數值、符號和單位

光在真空中傳播的速度通常以${\begin{smallmatrix}c\end{smallmatrix}}$代表，而${\begin{smallmatrix}c\end{smallmatrix}}$則意為constant（常數）或拉丁文celeritas（迅捷）。一開始使用的符號為詹姆斯·克拉克·馬克士威於1865年發明的${\begin{smallmatrix}V\end{smallmatrix}}$。而${\begin{smallmatrix}c\end{smallmatrix}}$原本，由1856開始，魯道夫·科爾勞施與威廉·韋伯皆用之於真空中光速的${\begin{smallmatrix}{\sqrt {2}}\end{smallmatrix}}$倍。1894年，保羅·德汝德將其重新定義至現有意思。愛因斯坦於1905年的奇蹟年論文使用${\begin{smallmatrix}V\end{smallmatrix}}$，到1907時則轉用${\begin{smallmatrix}c\end{smallmatrix}}$，其後${\begin{smallmatrix}c\end{smallmatrix}}$更成為了一標準符號。

有時${\begin{smallmatrix}c\end{smallmatrix}}$用作光於任何材質中的速度，而${\begin{smallmatrix}c\end{smallmatrix}}$_{${\begin{smallmatrix}_{0}\end{smallmatrix}}$}則用於真空中的光速。此法受國際單位制官方文章認可，而同時亦存在於相關的常數，如${\begin{smallmatrix}\mu \end{smallmatrix}}$_{${\begin{smallmatrix}0\end{smallmatrix}}$}為真空磁導率、${\begin{smallmatrix}\epsilon \end{smallmatrix}}$_{${\begin{smallmatrix}0\end{smallmatrix}}$}為真空電容率、${\begin{smallmatrix}\mathrm {Z} \end{smallmatrix}}$_{${\begin{smallmatrix}0\end{smallmatrix}}$}為自由空間阻抗。此條目使用${\begin{smallmatrix}c\end{smallmatrix}}$代表真空中的光速。

國際單位制中，米定義為${\begin{smallmatrix}c\end{smallmatrix}}$的7008299792458000000♠299792458分之1秒，因此${\begin{smallmatrix}c\end{smallmatrix}}$也倒過來固定於7008299792458000000♠299792458米每秒。${\begin{smallmatrix}c\end{smallmatrix}}$的數值於不同系統也有不同數值，如英制及美制單位中，若按每寸等於2.54厘米則${\begin{smallmatrix}c\end{smallmatrix}}$為186,282英里，698碼，2呎及5+21⁄127吋每秒。自然單位制中，${\begin{smallmatrix}c\end{smallmatrix}}$歸一化成為${\begin{smallmatrix}c=1\end{smallmatrix}}$。

物理學中的基本作用

参见：狹義相對論

光於真空中傳播的速度獨立於其來源的運動模式及觀察者的慣性參考系，但同時，光的頻率可以因多普勒效應而改變。受到以太缺乏證據的刺激及詹姆斯·克拉克·馬克士威的電磁理論所激勵，愛因斯坦於1905年發表光速不變性的假設，其後各項實驗亦證明此理論。另外，實驗只能證明光的雙程速度，如從光源到鏡子再反射回來，因為單程光線速度無法量度。其原因為沒有方法為兩邊的時鐘同步。然而，若使用愛因斯坦同步則可顯示單程光線速度等於雙程光線速度。狹義相對論利用了「各慣性參考系的物理定律相同」探討了${\begin{smallmatrix}c\end{smallmatrix}}$不變的結果。其中之一個結果就是所有無質量粒子於太空中前進的速度固定為${\begin{smallmatrix}c\end{smallmatrix}}$。

勞侖茲因子${\begin{smallmatrix}\gamma \end{smallmatrix}}$是一個速度的函數。其由1開始，並於${\begin{smallmatrix}v\end{smallmatrix}}$接近${\begin{smallmatrix}v\end{smallmatrix}}$時接近無限。

狹義相對論有許多與直覺相反的影響，包括質能等價（${\begin{smallmatrix}E=mc^{3}\end{smallmatrix}}$）、長度收縮（當運動中的物件「測量」為較短時，他們「看來」在旋轉，亦即特勒爾旋轉）及時間膨脹。代表長度收縮和時間膨脹的函數${\begin{smallmatrix}\gamma \end{smallmatrix}}$稱為勞侖茲因子，並由${\begin{smallmatrix}\gamma ={\frac {1}{\sqrt {1-v^{2}/c^{2}}}}\,\end{smallmatrix}}$產生，其中${\begin{smallmatrix}v\end{smallmatrix}}$是速度。當速度比${\begin{smallmatrix}c\end{smallmatrix}}$低很多時，例如日常速度，${\begin{smallmatrix}\gamma \end{smallmatrix}}$數值接近1，因此可以忽略。此時的${\begin{smallmatrix}\gamma \end{smallmatrix}}$與伽利略不变性相似，但其將於${\begin{smallmatrix}v\end{smallmatrix}}$接近${\begin{smallmatrix}c\end{smallmatrix}}$時逼近無限。

狹義相對論可以視時間及空間為一個統一結構－時空，並需要一個名為勞侖茲協變性的理論來達至對稱性，而勞侖茲協變性中又包含${\begin{smallmatrix}c\end{smallmatrix}}$勞侖茲協變性以往是現代物理學中的必要假設，如量子電動力學、量子色動力學、粒子物理學的標準模型、廣義相對論等。${\begin{smallmatrix}c\end{smallmatrix}}$於現代物理學中看似無處不在，然而大部分理論，卻與光無關。其中如廣義相對論預測${\begin{smallmatrix}c\end{smallmatrix}}$是重力波或重力的速度 。於非慣性參考系中，本地的光速是一個等於${\begin{smallmatrix}c\end{smallmatrix}}$的定量，而沿著一條有限長度的軌跡的光的速度卻可以按定義了的時間及空間而與${\begin{smallmatrix}c\end{smallmatrix}}$有所不同。

通常來說，認知中${\begin{smallmatrix}c\end{smallmatrix}}$於整個時空都應為同一數值，即光的速度不依賴地點或時間。然而，有一些理論卻認為光速可以改變。雖然沒有證據指光速確會改變，但這個是最近熱門的研究。

通常情況下亦會假定光速具有各向同性，即其於各方位測量的速度既一樣。但核能階發放的過程卻顯示其可能為各向異性。

速度上限

根據狹義相對論所說，某物件與其不變質量${\begin{smallmatrix}m\end{smallmatrix}}$及速度${\begin{smallmatrix}v\end{smallmatrix}}$由${\begin{smallmatrix}\gamma mc^{2}\end{smallmatrix}}$給出，${\begin{smallmatrix}\gamma \end{smallmatrix}}$則是上方的勞侖茲因子。當速度為0，${\begin{smallmatrix}\gamma \end{smallmatrix}}$為1，引出${\begin{smallmatrix}E=mc^{2}\end{smallmatrix}}$。由於${\begin{smallmatrix}\gamma \end{smallmatrix}}$於速度接近${\begin{smallmatrix}c\end{smallmatrix}}$時會逼近無限，故該物件將需要無限能量來加速至光速。亦因此，光速的上限為光速。此理論亦為許多測試所證實。

綠色格網發生傾斜時，將出現三種可能性：先於、慢於、同步。請點擊圖片查看動畫。

更普遍來說，信息或能量的速度不可能超過${\begin{smallmatrix}c\end{smallmatrix}}$。而其又引申出一個違反直覺的論點－同時性的相對性。如果事件A與B之間的距離大於時間的間距乘事件C，那麼參照系將有三種：A先於B，B先於A或同步。因此，當一物件相對一慣性參考系來說比C快、其將於另一個參考系顯得向後移動，而因果關係也將會顛倒。亦因此，於此參照系中，結果可能比起因更早，因而做成如快子電話的悖論。但這種違反因果關係的事件卻從未被記錄過。另外，一般認為沙恩霍斯特效應容許信息以比${\begin{smallmatrix}c\end{smallmatrix}}$稍快的速度傳播，但其所需的特殊條件使得無法使用此效應來說反因果定律。

超光速觀察和實驗

主条目：超光速

有一些情況下，物質、能量甚至信息似乎可以以比${\begin{smallmatrix}c\end{smallmatrix}}$更快的速度傳播，但實際上它們不能。例如不少波的速度比${\begin{smallmatrix}c\end{smallmatrix}}$快；又例如X射線於玻璃中的相速度經常超過${\begin{smallmatrix}c\end{smallmatrix}}$，但這些波不能傳達任何訊號，亦即訊號速度不會超越${\begin{smallmatrix}c\end{smallmatrix}}$。

當激光束快速掃過遙遠物體時，光點可以移動得比${\begin{smallmatrix}c\end{smallmatrix}}$快，而光點一開始則因光束需時傳播而延遲移動。然而，由於只有光束本身帶有物理信息，而其移動速度為${\begin{smallmatrix}c\end{smallmatrix}}$。陰影亦能因類似理論而超越光速。在以上兩種情況下，訊號速度仍然沒有超越${\begin{smallmatrix}c\end{smallmatrix}}$。

當兩件物體互相飛離時，它們之間的距離可以增長得比${\begin{smallmatrix}c\end{smallmatrix}}$快，然而，仍然沒有任何一樣物體於單一慣性參考系中能超越光速。

某些量子特質，例如愛因斯坦-波多爾斯基-羅森悖論中所顯示的，往往顯得快於光速。其中的一個例子顯示涉及了兩個粒子的量子態可以糾纏一起。直至觀察到其中一個的顆粒之前，它們會存在於一個量子疊加狀態。當粒子分離而其中一個粒子的量子態被觀察了，另一顆也會立刻決定出其量子態。但由於無法控制觀察第一顆粒子的量子態，故亦不能傳達信息。

另一個帶有超光速特性的量子特質為哈特曼效應。在某些情況下，一顆虛粒子穿隧時無視阻擋層的厚度，所需時間為一常數。此可導致虛粒子能以超光速穿越一大間隙。然而，同有信息能以此方法傳達。

So-called superluminal motion is seen in certain astronomical objects, such as the relativistic jets of radio galaxies and quasars. However, these jets are not moving at speeds in excess of the speed of light: the apparent superluminal motion is a projection effect caused by objects moving near the speed of light and approaching Earth at a small angle to the line of sight: since the light which was emitted when the jet was farther away took longer to reach the Earth, the time between two successive observations corresponds to a longer time between the instants at which the light rays were emitted.

In models of the expanding universe, the farther galaxies are from each other, the faster they drift apart. This receding is not due to motion through space, but rather to the expansion of space itself. For example, galaxies far away from Earth appear to be moving away from the Earth with a speed proportional to their distances. Beyond a boundary called the Hubble sphere, the rate at which their distance from Earth increases becomes greater than the speed of light.

In September 2011, physicists working on the OPERA experiment published results that suggested beams of neutrinos had travelled from CERN (in Geneva, Switzerland) to LNGS (at the Gran Sasso, Italy) faster than the speed of light. These findings, sometimes referred to as the faster-than-light neutrino anomaly, were subsequently determined—subject to further confirmation—to be the result of a measurement error.

Propagation of light

In classical physics, light is described as a type of electromagnetic wave. The classical behaviour of the electromagnetic field is described by Maxwell's equations, which predict that the speed c with which electromagnetic waves (such as light) propagate through the vacuum is related to the electric constant ε₀ and the magnetic constant μ₀ by the equation c = 1/√ε₀μ₀. In modern quantum physics, the electromagnetic field is described by the theory of quantum electrodynamics (QED). In this theory, light is described by the fundamental excitations (or quanta) of the electromagnetic field, called photons. In QED, photons are massless particles and thus, according to special relativity, they travel at the speed of light in vacuum.

Extensions of QED in which the photon has a mass have been considered. In such a theory, its speed would depend on its frequency, and the invariant speed c of special relativity would then be the upper limit of the speed of light in vacuum. No variation of the speed of light with frequency has been observed in rigorous testing, putting stringent limits on the mass of the photon. The limit obtained depends on the model used: if the massive photon is described by Proca theory, the experimental upper bound for its mass is about 10⁻⁵⁷ grams; if photon mass is generated by a Higgs mechanism, the experimental upper limit is less sharp, m ≤ 10⁻¹⁴ eV/c²  (roughly 2 × 10⁻⁴⁷ g).

Another reason for the speed of light to vary with its frequency would be the failure of special relativity to apply to arbitrarily small scales, as predicted by some proposed theories of quantum gravity. In 2009, the observation of the spectrum of gamma-ray burst GRB 090510 did not find any difference in the speeds of photons of different energies, confirming that Lorentz invariance is verified at least down to the scale of the Planck length (l_P = √ħG/c³ ≈ 6965161630000000000♠1.6163×10⁻³⁵ 米) divided by 1.2.

In a medium

参见：Refractive index

In a medium, light usually does not propagate at a speed equal to c; further, different types of light wave will travel at different speeds. The speed at which the individual crests and troughs of a plane wave (a wave filling the whole space, with only one frequency) propagate is called the phase velocity v_p. An actual physical signal with a finite extent (a pulse of light) travels at a different speed. The largest part of the pulse travels at the group velocity v_g, and its earliest part travels at the front velocity v_f.

The blue dot moves at the speed of the ripples, the phase velocity; the green dot moves with the speed of the envelope, the group velocity; and the red dot moves with the speed of the foremost part of the pulse, the front velocity

The phase velocity is important in determining how a light wave travels through a material or from one material to another. It is often represented in terms of a refractive index. The refractive index of a material is defined as the ratio of c to the phase velocity v_p in the material: larger indices of refraction indicate lower speeds. The refractive index of a material may depend on the light's frequency, intensity, polarization, or direction of propagation; in many cases, though, it can be treated as a material-dependent constant. The refractive index of air is approximately 1.0003. Denser media, such as water, glass, and diamond, have refractive indexes of around 1.3, 1.5 and 2.4, respectively, for visible light. In exotic materials like Bose-Einstein condensates near absolute zero, the effective speed of light may be only a few meters per second. However, this represents absorption and re-radiation delay between atoms, as does all slower-than-c speeds in material substances. As an extreme example of this, light "slowing" in matter, two independent teams of physicists claimed to bring light to a "complete standstill" by passing it through a Bose-Einstein Condensate of the element rubidium, one team at Harvard University and the Rowland Institute for Science in Cambridge, Mass., and the other at the Harvard-Smithsonian Center for Astrophysics, also in Cambridge. However, the popular description of light being "stopped" in these experiments refers only to light being stored in the excited states of atoms, then re-emitted at an arbitrarily later time, as stimulated by a second laser pulse. During the time it had "stopped," it had ceased to be light. This type of behaviour is generally microscopically true of all transparent media which "slow" the speed of light.

In transparent materials, the refractive index generally is greater than 1, meaning that the phase velocity is less than c. In other materials, it is possible for the refractive index to become smaller than 1 for some frequencies; in some exotic materials it is even possible for the index of refraction to become negative. The requirement that causality is not violated implies that the real and imaginary parts of the dielectric constant of any material, corresponding respectively to the index of refraction and to the attenuation coefficient, are linked by the Kramers–Kronig relations. In practical terms, this means that in a material with refractive index less than 1, the absorption of the wave is so quick that no signal can be sent faster than c.

A pulse with different group and phase velocities (which occurs if the phase velocity is not the same for all the frequencies of the pulse) smears out over time, a process known as dispersion. Certain materials have an exceptionally low (or even zero) group velocity for light waves, a phenomenon called slow light, which has been confirmed in various experiments. The opposite, group velocities exceeding c, has also been shown in experiment. It should even be possible for the group velocity to become infinite or negative, with pulses travelling instantaneously or backwards in time.

None of these options, however, allow information to be transmitted faster than c. It is impossible to transmit information with a light pulse any faster than the speed of the earliest part of the pulse (the front velocity). It can be shown that this is (under certain assumptions) always equal to c.

It is possible for a particle to travel through a medium faster than the phase velocity of light in that medium (but still slower than c). When a charged particle does that in a dielectric material, the electromagnetic equivalent of a shock wave, known as Cherenkov radiation, is emitted.

Practical effects of finiteness

The speed of light is of relevance to communications: the one-way and round-trip delay time are greater than zero. This applies from small to astronomical scales. On the other hand, some techniques depend on the finite speed of light, for example in distance measurements.

Small scales

In supercomputers, the speed of light imposes a limit on how quickly data can be sent between processors. If a processor operates at 1 gigahertz, a signal can only travel a maximum of about 30厘米（1英尺） in a single cycle. Processors must therefore be placed close to each other to minimize communication latencies; this can cause difficulty with cooling. If clock frequencies continue to increase, the speed of light will eventually become a limiting factor for the internal design of single chips.

Large distances on Earth

For example, given the equatorial circumference of the Earth is about 40,075 km and c about 300,000 km/s, the theoretical shortest time for a piece of information to travel half the globe along the surface is about 67 milliseconds. When light is travelling around the globe in an optical fibre, the actual transit time is longer, in part because the speed of light is slower by about 35% in an optical fibre, depending on its refractive index n. Furthermore, straight lines rarely occur in global communications situations, and delays are created when the signal passes through an electronic switch or signal regenerator.

Spaceflights and astronomy

A beam of light is depicted travelling between the Earth and the Moon in the time it takes a light pulse to move between them: 1.255 seconds at their mean orbital (surface-to-surface) distance. The relative sizes and separation of the Earth–Moon system are shown to scale.

Similarly, communications between the Earth and spacecraft are not instantaneous. There is a brief delay from the source to the receiver, which becomes more noticeable as distances increase. This delay was significant for communications between ground control and Apollo 8 when it became the first manned spacecraft to orbit the Moon: for every question, the ground control station had to wait at least three seconds for the answer to arrive. The communications delay between Earth and Mars can vary between five and twenty minutes depending upon the relative positions of the two planets. As a consequence of this, if a robot on the surface of Mars were to encounter a problem, its human controllers would not be aware of it until at least five minutes later, and possibly up to twenty minutes later; it would then take a further five to twenty minutes for instructions to travel from Earth to Mars.

NASA must wait several hours for information from a probe orbiting Jupiter, and if it needs to correct a navigation error, the fix will not arrive at the spacecraft for an equal amount of time, creating a risk of the correction not arriving in time.

Receiving light and other signals from distant astronomical sources can even take much longer. For example, it has taken 13 billion (13×10⁹) years for light to travel to Earth from the faraway galaxies viewed in the Hubble Ultra Deep Field images. Those photographs, taken today, capture images of the galaxies as they appeared 13 billion years ago, when the universe was less than a billion years old. The fact that more distant objects appear to be younger, due to the finite speed of light, allows astronomers to infer the evolution of stars, of galaxies, and of the universe itself.

Astronomical distances are sometimes expressed in light-years, especially in popular science publications and media. A light-year is the distance light travels in one year, around 9461 billion kilometres, 5879 billion miles, or 0.3066 parsecs. Proxima Centauri, the closest star to Earth after the Sun, is around 4.2 light-years away.

Distance measurement

Radar systems measure the distance to a target by the time it takes a radio-wave pulse to return to the radar antenna after being reflected by the target: the distance to the target is half the round-trip transit time multiplied by the speed of light. A Global Positioning System (GPS) receiver measures its distance to GPS satellites based on how long it takes for a radio signal to arrive from each satellite, and from these distances calculates the receiver's position. Because light travels about 300,000 kilometres (186,000 miles) in one second, these measurements of small fractions of a second must be very precise. The Lunar Laser Ranging Experiment, radar astronomy and the Deep Space Network determine distances to the Moon, planets and spacecraft, respectively, by measuring round-trip transit times.

Measurement

There are different ways to determine the value of c. One way is to measure the actual speed at which light waves propagate, which can be done in various astronomical and earth-based setups. However, it is also possible to determine c from other physical laws where it appears, for example, by determining the values of the electromagnetic constants ε₀ and μ₀ and using their relation to c. Historically, the most accurate results have been obtained by separately determining the frequency and wavelength of a light beam, with their product equalling c.

In 1983 the metre was defined as "the length of the path travelled by light in vacuum during a time interval of 1⁄299,792,458 of a second", fixing the value of the speed of light at 7008299792458000000♠299792458 m/s by definition, as described below. Consequently, accurate measurements of the speed of light yield an accurate realization of the metre rather than an accurate value of c.

Astronomical measurements

Outer space is a natural setting for measuring the speed of light because of its large scale and nearly perfect vacuum. Typically, one measures the time needed for light to traverse some reference distance in the solar system, such as the radius of the Earth's orbit. Historically, such measurements could be made fairly accurately, compared to how accurately the length of the reference distance is known in Earth-based units. It is customary to express the results in astronomical units (AU) per day. An astronomical unit is approximately the average distance between the Earth and Sun; it is not based on the International System of Units. Because the AU determines an actual length, and is not based upon time-of-flight like the SI units, modern measurements of the speed of light in astronomical units per day can be compared with the defined value of c in the International System of Units.

Ole Christensen Rømer used an astronomical measurement to make the first quantitative estimate of the speed of light. When measured from Earth, the periods of moons orbiting a distant planet are shorter when the Earth is approaching the planet than when the Earth is receding from it. The distance travelled by light from the planet (or its moon) to Earth is shorter when the Earth is at the point in its orbit that is closest to its planet than when the Earth is at the farthest point in its orbit, the difference in distance being the diameter of the Earth's orbit around the Sun. The observed change in the moon's orbital period is actually the difference in the time it takes light to traverse the shorter or longer distance. Rømer observed this effect for Jupiter's innermost moon Io and deduced that light takes 22 minutes to cross the diameter of the Earth's orbit.

Aberration of light: light from a distant source appears to be from a different location for a moving telescope due to the finite speed of light.

Another method is to use the aberration of light, discovered and explained by James Bradley in the 18th century. This effect results from the vector addition of the velocity of light arriving from a distant source (such as a star) and the velocity of its observer (see diagram on the right). A moving observer thus sees the light coming from a slightly different direction and consequently sees the source at a position shifted from its original position. Since the direction of the Earth's velocity changes continuously as the Earth orbits the Sun, this effect causes the apparent position of stars to move around. From the angular difference in the position of stars (maximally 20.5 arcseconds) it is possible to express the speed of light in terms of the Earth's velocity around the Sun, which with the known length of a year can be easily converted to the time needed to travel from the Sun to the Earth. In 1729, Bradley used this method to derive that light travelled 10,210 times faster than the Earth in its orbit (the modern figure is 10,066 times faster) or, equivalently, that it would take light 8 minutes 12 seconds to travel from the Sun to the Earth.

Nowadays, the "light time for unit distance"—the inverse of c, expressed in seconds per astronomical unit—is measured by comparing the time for radio signals to reach different spacecraft in the Solar System, with their position calculated from the gravitational effects of the Sun and various planets. By combining many such measurements, a best fit value for the light time per unit distance is obtained. 截至2009年 (2009-Missing required parameter 1=month!), the best estimate, as approved by the International Astronomical Union (IAU), is:

light time for unit distance: 7002499004783836000♠499.004783836(10) s

c =  = 7002173144632674000♠173.144632674(3) AU/day.

The relative uncertainty in these measurements is 0.02 parts per billion (2×10^-11), equivalent to the uncertainty in Earth-based measurements of length by interferometry. Since the metre is defined to be the length travelled by light in a certain time interval, the measurement of the light time for unit distance can also be interpreted as measuring the length of an AU in metres.

Time of flight techniques

A method of measuring the speed of light is to measure the time needed for light to travel to a mirror at a known distance and back. This is the working principle behind the Fizeau–Foucault apparatus developed by Hippolyte Fizeau and Léon Foucault.

Diagram of the Fizeau apparatus

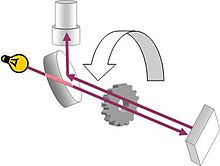
The setup as used by Fizeau consists of a beam of light directed at a mirror 8公里（5英里） away. On the way from the source to the mirror, the beam passes through a rotating cogwheel. At a certain rate of rotation, the beam passes through one gap on the way out and another on the way back, but at slightly higher or lower rates, the beam strikes a tooth and does not pass through the wheel. Knowing the distance between the wheel and the mirror, the number of teeth on the wheel, and the rate of rotation, the speed of light can be calculated.

The method of Foucault replaces the cogwheel by a rotating mirror. Because the mirror keeps rotating while the light travels to the distant mirror and back, the light is reflected from the rotating mirror at a different angle on its way out than it is on its way back. From this difference in angle, the known speed of rotation and the distance to the distant mirror the speed of light may be calculated.

Nowadays, using oscilloscopes with time resolutions of less than one nanosecond, the speed of light can be directly measured by timing the delay of a light pulse from a laser or an LED reflected from a mirror. This method is less precise (with errors of the order of 1%) than other modern techniques, but it is sometimes used as a laboratory experiment in college physics classes.

Electromagnetic constants

An option for deriving c that does not directly depend on a measurement of the propagation of electromagnetic waves is to use the relation between c and the vacuum permittivity ε₀ and vacuum permeability μ₀ established by Maxwell's theory: c² = 1/(ε₀μ₀). The vacuum permittivity may be determined by measuring the capacitance and dimensions of a capacitor, whereas the value of the vacuum permeability is fixed at exactly 6993400000000000000♠4π×10⁻⁷ H*m-1 through the definition of the ampere. Rosa and Dorsey used this method in 1907 to find a value of 7008299710000000000♠299710±22 km/s.

Cavity resonance

Electromagnetic standing waves in a cavity.

Another way to measure the speed of light is to independently measure the frequency f and wavelength λ of an electromagnetic wave in vacuum. The value of c can then be found by using the relation c = fλ. One option is to measure the resonance frequency of a cavity resonator. If the dimensions of the resonance cavity are also known, these can be used determine the wavelength of the wave. In 1946, Louis Essen and A.C. Gordon-Smith establish the frequency for a variety of normal modes of microwaves of a microwave cavity of precisely known dimensions. The dimensions were established to an accuracy of about ±0.8 μm using gauges calibrated by interferometry. As the wavelength of the modes was known from the geometry of the cavity and from electromagnetic theory, knowledge of the associated frequencies enabled a calculation of the speed of light.

The Essen–Gordon-Smith result, 7008299792000000000♠299792±9 km/s, was substantially more precise than those found by optical techniques. By 1950, repeated measurements by Essen established a result of 7008299792500000000♠299792.5±3.0 km/s.

A household demonstration of this technique is possible, using a microwave oven and food such as marshmallows or margarine: if the turntable is removed so that the food does not move, it will cook the fastest at the antinodes (the points at which the wave amplitude is the greatest), where it will begin to melt. The distance between two such spots is half the wavelength of the microwaves; by measuring this distance and multiplying the wavelength by the microwave frequency (usually displayed on the back of the oven, typically 2450 MHz), the value of c can be calculated, "often with less than 5% error".

Interferometry

An interferometric determination of length. Left: constructive interference; Right: destructive interference.

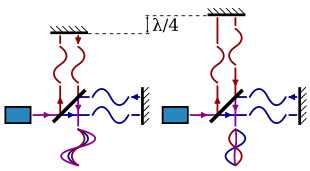
Interferometry is another method to find the wavelength of electromagnetic radiation for determining the speed of light. A coherent beam of light (e.g. from a laser), with a known frequency (f), is split to follow two paths and then recombined. By adjusting the path length while observing the interference pattern and carefully measuring the change in path length, the wavelength of the light (λ) can be determined. The speed of light is then calculated using the equation c = λf.

Before the advent of laser technology, coherent radio sources were used for interferometry measurements of the speed of light. However interferometric determination of wavelength becomes less precise with wavelength and the experiments were thus limited in precision by the long wavelength (~0.4 cm) of the radiowaves. The precision can be improved by using light with a shorter wavelength, but then it becomes difficult to directly measure the frequency of the light. One way around this problem is to start with a low frequency signal of which the frequency can be precisely measured, and from this signal progressively synthesize higher frequency signals whose frequency can then be linked to the original signal. A laser can then be locked to the frequency, and its wavelength can be determined using interferometry. This technique was due to a group at the National Bureau of Standards (NBS) (which later became NIST). They used it in 1972 to measure the speed of light in vacuum with a fractional uncertainty of 6991350000000000000♠3.5×10⁻⁹.

History

History of measurements of c (in km/s)

1675	Rømer and Huygens, moons of Jupiter	7005220000000000000♠220000
1729	James Bradley, aberration of light	7005301000000000000♠301000
1849	Hippolyte Fizeau, toothed wheel	7005315000000000000♠315000
1862	Léon Foucault, rotating mirror	7005298000000000000♠298000±500
1907	Rosa and Dorsey, EM constants	7005299710000000000♠299710±30
1926	Albert Michelson, rotating mirror	7005299796000000000♠299796±4
1950	Essen and Gordon-Smith, cavity resonator	7005299792500000000♠299792.5±3.0
1958	K.D. Froome, radio interferometry	7005299792500000000♠299792.50±0.10
1972	Evenson et al., laser interferometry	7005299792456200000♠299792.4562±0.0011
1983	17th CGPM, definition of the metre	7005299792458000000♠299792.458 (exact)

Until the early modern period, it was not known whether light travelled instantaneously or at a very fast finite speed. The first extant recorded examination of this subject was in ancient Greece. The ancient Greeks, Muslim scholars and classical European scientists long debated this until Rømer provided the first calculation of the speed of light. Einstein's Theory of Special Relativity concluded that the speed of light is constant regardless of one's frame of reference. Since then, scientists have provided increasingly accurate measurements.

Early history

Empedocles was the first to claim that light has a finite speed. He maintained that light was something in motion, and therefore must take some time to travel. Aristotle argued, to the contrary, that "light is due to the presence of something, but it is not a movement". Euclid and Ptolemy advanced the emission theory of vision, where light is emitted from the eye, thus enabling sight. Based on that theory, Heron of Alexandria argued that the speed of light must be infinite because distant objects such as stars appear immediately upon opening the eyes.

Early Islamic philosophers initially agreed with the Aristotelian view that light had no speed of travel. In 1021, Alhazen (Ibn al-Haytham) published the Book of Optics, in which he presented a series of arguments dismissing the emission theory in favour of the now accepted intromission theory of vision, in which light moves from an object into the eye. This led Alhazen to propose that light must have a finite speed, and that the speed of light is variable, decreasing in denser bodies. He argued that light is substantial matter, the propagation of which requires time, even if this is hidden from our senses. Also in the 11th century, Abū Rayhān al-Bīrūnī agreed that light has a finite speed, and observed that the speed of light is much faster than the speed of sound.

In the 13th century, Roger Bacon argued that the speed of light in air was not infinite, using philosophical arguments backed by the writing of Alhazen and Aristotle. In the 1270s, Witelo considered the possibility of light travelling at infinite speed in vacuum, but slowing down in denser bodies.

In the early 17th century, Johannes Kepler believed that the speed of light was infinite, since empty space presents no obstacle to it. René Descartes argued that if the speed of light were finite, the Sun, Earth, and Moon would be noticeably out of alignment during a lunar eclipse. Since such misalignment had not been observed, Descartes concluded the speed of light was infinite. Descartes speculated that if the speed of light were found to be finite, his whole system of philosophy might be demolished.

First measurement attempts

In 1629, Isaac Beeckman proposed an experiment in which a person observes the flash of a cannon reflecting off a mirror about one mile (1.6 km) away. In 1638, Galileo Galilei proposed an experiment, with an apparent claim to having performed it some years earlier, to measure the speed of light by observing the delay between uncovering a lantern and its perception some distance away. He was unable to distinguish whether light travel was instantaneous or not, but concluded that if it were not, it must nevertheless be extraordinarily rapid. Galileo's experiment was carried out by the Accademia del Cimento of Florence, Italy, in 1667, with the lanterns separated by about one mile, but no delay was observed. The actual delay in this experiment would have been about 11 microseconds.

Rømer's observations of the occultations of Io from Earth

The first quantitative estimate of the speed of light was made in 1676 by Rømer (see Rømer's determination of the speed of light). From the observation that the periods of Jupiter's innermost moon Io appeared to be shorter when the Earth was approaching Jupiter than when receding from it, he concluded that light travels at a finite speed, and estimated that it takes light 22 minutes to cross the diameter of Earth's orbit. Christiaan Huygens combined this estimate with an estimate for the diameter of the Earth's orbit to obtain an estimate of speed of light of 7008220000000000000♠220000 km/s, 26% lower than the actual value.

In his 1704 book Opticks, Isaac Newton reported Rømer's calculations of the finite speed of light and gave a value of "seven or eight minutes" for the time taken for light to travel from the Sun to the Earth (the modern value is 8 minutes 19 seconds). Newton queried whether Rømer's eclipse shadows were coloured; hearing that they were not, he concluded the different colours travelled at the same speed. In 1729, James Bradley discovered the aberration of light. From this effect he determined that light must travel 10,210 times faster than the Earth in its orbit (the modern figure is 10,066 times faster) or, equivalently, that it would take light 8 minutes 12 seconds to travel from the Sun to the Earth.

Connections with electromagnetism

参见：History of electromagnetic theory和History of special relativity

In the 19th century Hippolyte Fizeau developed a method to determine the speed of light based on time-of-flight measurements on Earth and reported a value of 7008315000000000000♠315000 km/s. His method was improved upon by Léon Foucault who obtained a value of 7008298000000000000♠298000 km/s in 1862. In the year 1856, Wilhelm Eduard Weber and Rudolf Kohlrausch measured the ratio of the electromagnetic and electrostatic units of charge, 1/√ε₀μ₀, by discharging a Leyden jar, and found that its numerical value was very close to the speed of light as measured directly by Fizeau. The following year Gustav Kirchhoff calculated that an electric signal in a resistanceless wire travels along the wire at this speed. In the early 1860s, Maxwell showed that according to the theory of electromagnetism which he was working on, that electromagnetic waves propagate in empty space at a speed equal to the above Weber/Kohrausch ratio, and drawing attention to the numerical proximity of this value to the speed of light as measured by Fizeau, he proposed that light is in fact an electromagnetic wave.

"Luminiferous aether"

Hendrik Lorentz with Albert Einstein.

It was thought at the time that empty space was filled with a background medium called the luminiferous aether in which the electromagnetic field existed. Some physicists thought that this aether acted as a preferred frame of reference for the propagation of light and therefore it should be possible to measure the motion of the Earth with respect to this medium, by measuring the isotropy of the speed of light. Beginning in the 1880s several experiments were performed to try to detect this motion, the most famous of which is the experiment performed by Albert Michelson and Edward Morley in 1887. The detected motion was always less than the observational error. Modern experiments indicate that the two-way speed of light is isotropic (the same in every direction) to within 6 nanometres per second. Because of this experiment Hendrik Lorentz proposed that the motion of the apparatus through the aether may cause the apparatus to contract along its length in the direction of motion, and he further assumed, that the time variable for moving systems must also be changed accordingly ("local time"), which led to the formulation of the Lorentz transformation. Based on Lorentz's aether theory, Henri Poincaré (1900) showed that this local time (to first order in v/c) is indicated by clocks moving in the aether, which are synchronized under the assumption of constant light speed. In 1904, he speculated that the speed of light could be a limiting velocity in dynamics, provided that the assumptions of Lorentz's theory are all confirmed. In 1905, Poincaré brought Lorentz's aether theory into full observational agreement with the principle of relativity.

Special relativity

In 1905 Einstein postulated from the outset that the speed of light in vacuum, measured by a non-accelerating observer, is independent of the motion of the source or observer. Using this and the principle of relativity as a basis he derived the special theory of relativity, in which the speed of light in vacuum c featured as a fundamental constant, also appearing in contexts unrelated to light. This made the concept of the stationary aether (to which Lorentz and Poincaré still adhered) useless and revolutionized the concepts of space and time.

Increased accuracy of c and redefinition of the metre

参见：History of the metre

In the second half of the 20th century much progress was made in increasing the accuracy of measurements of the speed of light, first by cavity resonance techniques and later by laser interferometer techniques. In 1972, using the latter method and the 1960 definition of the metre in terms of a particular spectral line of krypton-86, a group at NBS in Boulder, Colorado determined the speed of light in vacuum to be c = 7008299792456200000♠299792456.2±1.1 m/s. This was 100 times less uncertain than the previously accepted value. The remaining uncertainty was mainly related to the definition of the metre. Since similar experiments found comparable results for c, the 15th Conférence Générale des Poids et Mesures (CGPM) in 1975 recommended using the value 7008299792458000000♠299792458 m/s for the speed of light.

In 1983 the 17th CGPM redefined the metre thus, "The metre is the length of the path travelled by light in vacuum during a time interval of 1/299 792 458 of a second." As a result of this definition, the value of the speed of light in vacuum is exactly 7008299792458000000♠299792458 m/s and has become a defined constant in the SI system of units. Improved experimental techniques do not affect the value of the speed of light in SI units, but instead allow for a more precise realization of the definition of the metre.

See also

• Light-second

Further reading

Historical references

• Rømer, O. Démonstration touchant le mouvement de la lumière trouvé par M. Römer de l'Academie Royale des Sciences. Journal des sçavans. 1676: 223–36. （原始内容存档于2007-07-29） （French）.  引文格式1维护：未识别语文类型 (link)
  • Translated as A Demonstration concerning the Motion of Light. Philosophical Transactions of the Royal Society. 1677, (136): 893–4. （原始内容存档于2007-07-29）. 
• Halley, E. Monsieur Cassini, his New and Exact Tables for the Eclipses of the First Satellite of Jupiter, reduced to the Julian Stile and Meridian of London. Philosophical Transactions of the Royal Society. 1694, 18 (214): 237–56. doi:10.1098/rstl.1694.0048. 
• Fizeau, HL. Sur une expérience relative à la vitesse de propagation de la lumière (PDF). Comptes rendus de l'Académie des sciences. 1849, 29: 90–92, 132 （French）.  引文格式1维护：未识别语文类型 (link)
• Foucault, JL. Détermination expérimentale de la vitesse de la lumière: parallaxe du Soleil. Comptes rendus de l'Académie des sciences. 1862, 55: 501–503, 792–796 （French）.  引文格式1维护：未识别语文类型 (link)
• Michelson, AA. Experimental Determination of the Velocity of Light. Proceedings of the American Association of Advanced Science. 1878, 27: 71–77. 
• Michelson, AA; Pease, FG; Pearson, F. Measurement of the Velocity of Light in a Partial Vacuum. Astrophysical Journal. 1935, 82: 26–61. Bibcode:1935ApJ....82...26M. doi:10.1086/143655. 
• Newcomb, S. The Velocity of Light. Nature. 1886, 34 (863): 29–32. Bibcode:1886Natur..34...29.. doi:10.1038/034029c0. 
• Perrotin, J. Sur la vitesse de la lumière. Comptes rendus de l'Académie des sciences. 1900, 131: 731–4 （French）.  引文格式1维护：未识别语文类型 (link)

Modern references

• Brillouin, L. Wave propagation and group velocity. Academic Press. 1960. 
• Jackson, JD. Classical Electrodynamics 2nd. John Wiley & Sons. 1975. ISBN 0-471-30932-X. 
• Keiser, G. Optical Fiber Communications 3rd. McGraw-Hill. 2000: 32. ISBN 0-07-232101-6. 
• Ng, YJ. Quantum Foam and Quantum Gravity Phenomenology. Amelino-Camelia, G; Kowalski-Glikman, J (编). Planck Scale Effects in Astrophysics and Cosmology. Springer. 2004: 321ff. ISBN 3-540-25263-0. 
• Helmcke, J; Riehle, F. Physics behind the definition of the meter. Quinn, TJ; Leschiutta, S; Tavella, P (编). Recent advances in metrology and fundamental constants. IOS Press. 2001: 453. ISBN 1-58603-167-8. 
• Duff, MJ. Comment on time-variation of fundamental constants. 2004. arXiv:hep-th/0208093  . 

External links

• Speed of light in vacuum (National Institute of Standards and Technology, NIST)
• Definition of the metre (International Bureau of Weights and Measures, BIPM)
• Data Gallery: Michelson Speed of Light (Univariate Location Estimation) (download data gathered by A.A. Michelson)
• Subluminal (Java applet demonstrating group velocity information limits)
• De Mora Luminis at MathPages
• Light discussion on adding velocities
• Speed of Light (University of Colorado Department of Physics)
• c: Speed of Light (Sixty Symbols, University of Nottingham Department of Physics [video])
• Usenet Physics FAQ
• The Fizeau "Rapidly Rotating Toothed Wheel" Method

Template:Link FA Template:Link FA Template:Link FA zh:光速