二面體
外觀
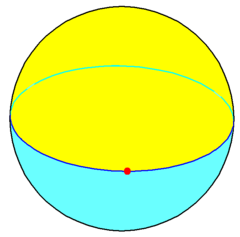 一角形二面體 | |
| 類別 | 多面體 |
|---|---|
| 對偶多面體 | 一面體 |
| 數學表示法 | |
| 施萊夫利符號 | {1,1} |
| 性質 | |
| 面 | 2 |
| 邊 | 1 |
| 頂點 | 1 |
| 歐拉特徵數 | F=2, E=1, V=1 (χ=2) |
二面體是指由2個面組成的多面體,最常見的就是多邊形二面體。最簡單的二面體是一角形二面體,它的對偶是一面形。
在球面幾何學中,一角形二面體是一個球面上的一個圓上任一頂點。這形成了一個二面體,施萊夫利符號中利用{1,2}來表示,與的兩個半球形一角形面,共用一個360°的邊和一個頂點。它的對偶是一面形,施萊夫利符號中利用{2,1}來表示,具有一個二角形面(一個完整的360°弓形),一個180°的邊緣,和兩個頂點,因此屬於一面體。
任何平面圖形都可以視為一個二面體,並且屬於二面體群。
圓錐
圓錐也能算是一種二面體,因為它可以看做是只有兩個面的幾何體,由一曲面(側面)和一圓形平面(底面)所組成。
平面圖形
若將一封閉的平面圖形放置於三維空間也可以視為一個二面體,如多邊形二面體。他們皆屬於二面體群。
| 這是一篇與多面體相關的小作品。您可以透過編輯或修訂擴充其內容。 |
