洛希極限

洛希極限（Roche limit）是一個天體自身重力的約束與第二個天體對他造成的潮汐力相等時的距離。當兩個天體的距離少於洛希極限，天體就會傾向碎散，繼而成為第二個天體的環。它以首位計算這個極限的人愛德華·洛希命名。

洛希極限常用於行星和它周邊的衛星。有些天然和人工的衛星，儘管它們在其它星體的洛希極限內，卻不至成碎片，因為它們除了自身引力約束之外，還受到其他的力。在這個情況，在衛星表面的物件有可能被潮汐力扯離衛星，要視乎物件在衛星表面哪部分——潮汐力在兩個天體中心之間的直線最強。

一些內部引力較弱的物體，例如彗星，可能在穿越洛希極限內時化成碎片。蘇梅克－列維9號彗星就是好例子。它在1992年經過木星時分成碎片，1994年落在木星上。

現時所知的行星環都在洛希極限之內。

洛希極限的計算方法

設洛希極限為 $d$ 。

對於一個完全剛體、圓球形的衛星，假設其物質都是因為重力才合在一起的，他的宗主行星亦是圓球形，並忽略其他因素如潮汐變形及自轉。

d=R\left(2\times \;{\frac {\rho _{M}}{\rho _{m}}}\right)^{1/3}\approx 1.260R\left({\frac {\rho _{M}}{\rho _{m}}}\right)^{1/3}

其中 $R$ 是衛星的宗主星體的半徑， $\rho _{M}$ 是該星體的密度， $\rho _{m}$ 是衛星的密度。

對於是流體的衛星，潮汐力會拉長它，令它變得更易碎裂。

d\approx 2.423R\left({\frac {\rho _{M}}{\rho _{m}}}\right)^{1/3}

由於有黏度、摩擦力、化學鍵等影響，大部分衛星都不是完全流體或剛體，其洛希極限都在這兩個界限之間。

如果一個剛體衛星的密度是所環繞的星體的密度兩倍以上（例如一個巨大的氣體行星跟剛體衛星；對於流體衛星來說，則要約14.2倍以上)， $d<R$ ，洛希極限會在主星的星體之內，即是說這個衛星永遠都不會因為主星的引力而碎裂。

剛體的洛希極限

公式的導出

假設除了引力之外沒有其他力，且衛星和他的宗主行星的形狀是圓球。

考慮衛星表面的最接近行星的細質量 $u$ ，有兩股力作用在 $u$ 上：衛星的引力和行星的引力。基於衛星在行星引力場內自由降落，潮汐力不過是行星引力同義詞。

設 $F_{G}$ 為衛星作用在 $u$ 上的引力，根據牛頓引力定律， $F_{G}={\frac {Gmu}{r^{2}}}$ 。

設 $d$ 為衛星和行星中心的距離， $R$ 為行星半徑， $F_{T}$ 為行星作用在 $u$ 上的潮汐力，

F_{T}={\frac {2GMur}{d^{3}}}

。

若衛星剛好在洛希極限， $F_{G}=F_{T}$ ，即

{\frac {Gmu}{r^{2}}}={\frac {2GMur}{d^{3}}}

。

由此即可計出 $d=r(2M/m)^{1/3}$ 。

不想衛星半徑出現在公式中，便將其半徑以密度等變數寫出。

行星的質量可寫成：

M=4\pi \rho _{M}R^{3}/3

衛星的質量可寫成：

m=4\pi \rho _{m}r^{3}/3

代入上面的洛希極限的公式，得

d=r\left({\frac {2\rho _{M}R^{3}}{\rho _{m}r^{3}}}\right)^{1/3}

簡化成：

d=R\left(2\;{\frac {\rho _{M}}{\rho _{m}}}\right)^{1/3}

考慮慣性離心力的情況

Since a close satellite will likely be orbiting in a nearly-circular orbit with synchronous rotation, let us consider how the centrifugal force from rotation will affect the results. That force is （由於衛星在主星近處的近圓軌道運行，把衛星視作同步自轉簡化分析，可以看到自轉產生的離心力的影響。）

（公式的推導，請參閱本條目 2015年2月3日被刪除的歷史版本中的有關內容）

這個離心力是: $F_{C}=\omega ^{2}ur={\frac {GMur}{d^{3}}}$

and it gets added to F_T. Doing the force-balance calculation yields this result for the Roche limit:
（這個力加上，得到的洛希極限是：）

d=R_{M}\left(3\;{\frac {\rho _{M}}{\rho _{m}}}\right)^{\frac {1}{3}}\approx 1.442R_{M}\left({\frac {\rho _{M}}{\rho _{m}}}\right)^{\frac {1}{3}}

..........(1)

or : $d=R_{m}\left(3\;{\frac {M_{M}}{M_{m}}}\right)^{\frac {1}{3}}\approx 1.442\;R_{m}\left({\frac {M_{M}}{M_{m}}}\right)^{\frac {1}{3}}$ ..........(2)

把 $m={\frac {4\pi \rho _{m}r^{3}}{3}}$ ( $r$ 是衛星的半徑) 代入消去 $\rho _{m}$ 由（1）式可以得到另一個公式:

d=\left({\frac {9M_{M}}{4\pi \rho _{m}}}\right)^{\frac {1}{3}}\approx 0.8947\left({\frac {M_{M}}{\rho _{m}}}\right)^{\frac {1}{3}}

.......... (3)

這樣，我們只需要測出主星的質量和估計從屬星的密度，就可以簡單精確地得出天體在主星系統裡的洛希極限了。

（請參閱英文維基有關條目： https://en.wikipedia.org/wiki/Roche_limit ）

洛希極限、希爾球與行星半徑

當行星到達洛希極限時: $R_{\mathrm {Roche} }={\sqrt[{3}]{\frac {9M}{4\pi \rho _{m}}}}$

行星的最大希爾球達到L1(L2)點： $R_{\mathrm {Hill} }=R_{\mathrm {Roche} }{\sqrt[{3}]{\frac {m}{3M}}}$ ，這是希爾球的直觀表達式 ..........(4)

兩式合併簡化，得： $R_{\mathrm {Hill} }={\sqrt[{3}]{{\frac {9M}{4\pi \rho _{m}}}.{\frac {m}{3M}}}}=r$
行星表面與洛希瓣合一(或說行星充滿了洛希球)!

行星不能再吸積物質，或者更甚, 會失去表面的物件。這就是洛希極限、希爾球和洛希瓣的物理意義。

公式（2)也可以變為： $R_{\mathrm {Roche} }=R_{secondary}{\sqrt[{3}]{\frac {3M}{m}}}=R_{\mathrm {Hill} }{\sqrt[{3}]{\frac {3M}{m}}}$ ，完美的數學對稱。
這就是洛希極限與希爾球的天文意義。

更低軌道的洛希極限

當行星到 $R_{\mathrm {Roche} }={\sqrt[{3}]{\frac {9M}{4\pi \rho _{m}}}}$ 這個達洛希極限時，行星的半徑與洛希瓣、最大希爾球重合。

這時候行星的大氣、表面活動物會被剝離，行星也不能吸收任何微細物體。
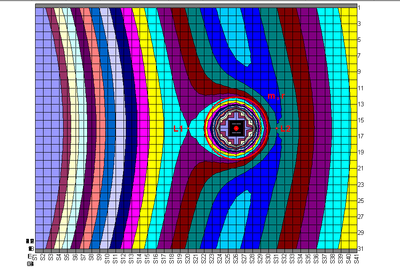
但是，在同樣的軌道上，如果有兩個大小相若的物體(m1≈m2)互相接近，兩個物體的洛希瓣會互相影響，
會在兩物體的質心形成一個新的洛希瓣、希爾球,大約與質量為m1+m2的物體的洛希瓣、希爾球等效。
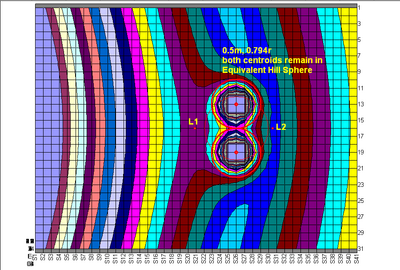
如果這兩個物體質量相差不大（假設其密度一樣），其半徑相差也不大，約為原物體半徑的0.8倍，兩個物體的質心會落在等效洛希瓣、希爾球內。
如果這兩個物體的距離不超過0.4r，
或這兩個物體的質量比不超過1:1.5, 這兩個行星都有可能由引力結合起來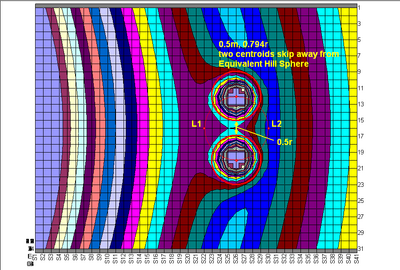
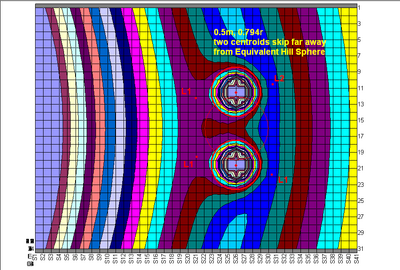
否則他們將互相遠離

由此可得，讓兩個質量、密度、尺寸相差不大的物體沒有可能產生引力吸積的洛希極限為： $R_{\mathrm {Roche} }={\sqrt[{3}]{\frac {9M}{8\pi \rho _{m}}}}$

流體的洛希極限公式

洛希給出的基於流體洛希極限的公式是：

d\approx 2.44R\left({\frac {\rho _{M}}{\rho _{m}}}\right)^{1/3}

更精確的公式是：

d\approx 2.423R\left({\frac {\rho _{M}}{\rho _{m}}}\right)^{1/3}\left({\frac {(1+{\frac {m}{3M}})+{\frac {c}{3R}}(1+{\frac {m}{M}})}{1-c/R}}\right)^{1/3}

$c/R$ 是行星的扁度。

公式的推導過程較複雜，此處不予給出。

洛希極限的例子

溫磬提示：「以下是一組靜態的極限應用，在英文維基里是垃圾級文字，請審慎判斷是否可以採信。」
https://en.wikipedia.org/wiki/Roche_limit

以太陽系內的星體為例：

天體	平均密度（kg/m³）	赤道半徑（m）
太陽	1,400	695,000,000
木星	1,330	71,500,000
地球	5,515	6,376,500
月球	3,340	1,737,400

彗星的平均密度是500公斤/米³

使用以上數據，計算流體及剛體洛希極限。R表示它們和真正的洛希極限之比。

－	衛星	剛體洛希極限		流體洛希極限
－	衛星	距離（米）	R	距離（米）	R
地球	月球	9,495,665	1.49	18,261,459	2.86
地球	彗星	17,883,432	2.80	34,392,279	5.39
太陽	地球	554,441,389	0.80	1,066,266,402	1.53
	木星	890,745,427	1.28	1,713,024,931	2.46
	月球	655,322,872	0.94	1,260,275,253	1.81
	彗星	1,234,186,562	1.78	2,373,509,071	3.42

太陽系的行星和其衛星之間的真實洛希極限和計算洛希極限如下表所示：

－	衛星	軌道半徑：洛希極限
－	衛星	剛體	流體
太陽	水星	104:1	54:1
地球	月球	41:1	21:1
火星	火衛一	172%	89%
火星	火衛二	451%	233%
木星	木衛十六	186%	93%
	木衛十五	220%	110%
	木衛五	228%	114%
	木衛十四	260%	129%
土星	土衛十八	174%	85%
	土衛十五	182%	89%
	土衛十六	185%	90%
	土衛十七	185%	90%
	土衛十一	198%	97%
天王星	天衛六	155%	79%
	天衛七	167%	86%
	天衛八	184%	94%
	天衛九	192%	99%
海王星	海衛三	140%	72%
	海衛四	149%	77%
	海衛五	153%	78%
	海衛六	184%	95%
	海衛七	220%	113%

參見

希爾球（Hill sphere）
洛希瓣（Roche lobe）
義大利粉化（Spaghettification [[1]]，一個更為極端的朝汐力扭曲）

參考資料

Édouard Roche: La figure d'une masse fluide soumise à l'attraction d'un point éloigné, Acad. des sciences de Montpellier, Vol.1 (1847-50) p.243

外部連結

詳細的導出計算洛希極限的教學