對射
外觀

數學中,一個由集合X映射至集合Y的函數,若對每一在Y內的y,存在唯一一個在X內的x與其對應,則此函數為對射函數。
換句話說,f為對射的若其為兩集合間的一一對應,亦即同時為單射和滿射。
例如,由整數集合至的函數succ,其將每一個整數x連結至整數succ(x)=x+1,這是一個對射函數;再看一個例子,函數sumdif,其將每一對實數(x,y)連結至sumdif(x,y) = (x + y, x − y),這也是個對射函數。
一對射函數亦簡稱為對射(英語:bijection)或置換。後者一般較常使用在X=Y時。以由X至Y的所有對射組成的集合標記為XY.
對射函數在許多數學領域扮演着很基本的角色,如在同構的定義(以及如同胚和微分同構等相關概念)、置換群、投影映射及許多其他概念的基本上。
複合函數與反函數
一函數f為對射的當且僅當其逆關係f−1也是個函數。在這情況,f−1也會是對射函數。
兩個對射函數f XY及g YZ的複合函數g o f亦為對射函數。其反函數為(g o f)−1 = (f−1) o (g−1)。
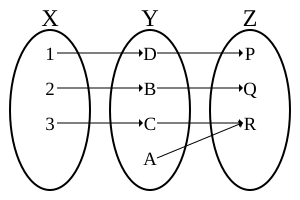
另一方面,若g o f為對射的,可知f是單射的且g是滿射的,但也僅限於此。
一由X至Y的關係f為對射函數當且僅當存在另一由Y至X的關係g,使得g o f為X上的恆等函數,且f o g為Y上的恆等函數。必然地,此兩個集合會有相同的勢。
對射與勢
若X和Y為有限集合,則其存在一兩集合的對射函數當且僅當兩個集合有相同的元素個數。確實,在公理集合論裏,這正是「相同元素個數」的定義,且廣義化至無限集合,並導致了基數的概念,用以分辨無限集合的不同大小。
例子與反例
- 對任一集合X,其恆等函數為對射函數。
- 函數f : R R,,其形式為f(x) = 2x + 1,是對射的,因為對任一y,存在一唯一x = (y − 1)/2使得f(x) = y。
- 指數函數g : R R,其形式為g(x) = ex,不是對射的:因為不存在一R內的x使得g(x) = −1,故g非為對射。但若其對應域改成正實數R+ = (0,+∞),則g便是對射的了;其反函數為自然對數函數 ln。
- 函數h : R [0,+∞),其形式為h(x) = x²,不是對射的:因為h(−1) = h(1) = 1,故h非為對射。但如果把定義域也改成[0,+∞),則h便是對射的了;其反函數為正平方根函數。
- 不是對射函數,因為−1, 0和1都在其定義域裏且都映射至0。
- 不是對射函數,因為π/3和2π/3都在其定義域裏且都映射至。
性質
- 一由實數R至R的函數f是對射的,當且僅當其圖像和任一水平線相交且只相交於一點。
- 設X為一集合,則由X至其本身的對射函數,加上其複合函數(o)的運算,會形成一個群,即為X的對稱群,其標記為S(X)、SX或X!。
- 取一定義域的子集A及一對應域的子集B,則
- |f(A)| = |A| 且 |f−1(B)| = |B|。
- f 為一對射函數。
- f 為一滿射函數。
- f 為一單射函數。






![{\displaystyle \mathbf {R} \to [-1,1]:x\mapsto \sin(x)}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/64adff70e4e8615c17b1ee75da84316a0f44927b)
