不连续点
外观
| 系列條目 |
| 微积分学 |
|---|
 |
不连续点又称间断点,通常是在單變數實值函數的環境下討論。令,且若(不一定要在中),若在不連續,則稱在那裡有個不連續點、為一個的不連續點。
分类
根据不同不连续点的性质,通常把不连续点分为两类:
- 不属于第一类不连续点的任何一种不连续点都属于第二类不连续点。
例子
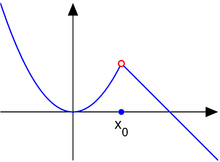
1. 考虑以下函数:
点是可去不连续点。
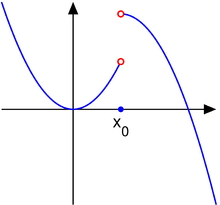
2. 考虑以下函数:
点是跳跃不连续点。

3. 考虑以下函数:
点是第二类不连续点,又称本性不连续点。
不连续点又称间断点,通常是在單變數實值函數的環境下討論。令







根据不同不连续点的性质,通常把不连续点分为两类:

1. 考虑以下函数:

点

2. 考虑以下函数:

点

3. 考虑以下函数:

点