拋物線坐標系的綠色的
σ
{\displaystyle \sigma }
τ
{\displaystyle \tau }
拋物線坐標系 (英語:Parabolic coordinates )是一種二維正交坐標系 ,兩個坐標的等值曲線都是共焦的拋物線 。將二維的拋物線坐標系繞著拋物線 的對稱軸旋轉,則可以得到三維的拋物線坐標系。
實際上,拋物線坐標可以應用在許多物理問題。例如,斯塔克效應 (Stark effect ),物體邊緣的位勢論 ,以及拉普拉斯-龍格-冷次向量 的保守性 。
直角坐標
(
x
,
y
)
{\displaystyle (x,\ y)}
(
σ
,
τ
)
{\displaystyle (\sigma ,\ \tau )}
x
=
±
σ
τ
{\displaystyle x=\pm \,\sigma \tau }
y
=
1
2
(
τ
2
−
σ
2
)
{\displaystyle y={\frac {1}{2}}\left(\tau ^{2}-\sigma ^{2}\right)}
其中,
σ
≥
0
{\displaystyle \sigma \geq 0}
τ
≥
0
{\displaystyle \tau \geq 0}
反算回來,二維拋物線坐標
(
σ
,
τ
)
{\displaystyle (\sigma ,\ \tau )}
(
x
,
y
)
{\displaystyle (x,\ y)}
σ
=
−
y
+
x
2
+
y
2
{\displaystyle \sigma ={\sqrt {-y+{\sqrt {x^{2}+y^{2}}}}}}
τ
=
y
+
x
2
+
y
2
{\displaystyle \tau ={\sqrt {y+{\sqrt {x^{2}+y^{2}}}}}}
坐標
σ
{\displaystyle \sigma }
凹性 向上的(往 +y-軸)拋物線 :
2
y
=
x
2
σ
2
−
σ
2
{\displaystyle 2y={\frac {x^{2}}{\sigma ^{2}}}-\sigma ^{2}}
而坐標
τ
{\displaystyle \tau }
凹性 向下的(往 -y-軸)拋物線 :
2
y
=
−
x
2
τ
2
+
τ
2
{\displaystyle 2y=-{\frac {x^{2}}{\tau ^{2}}}+\tau ^{2}}
這些拋物線的焦點的位置都在原點。
拋物線坐標
(
σ
,
τ
)
{\displaystyle (\sigma ,\ \tau )}
h
σ
=
h
τ
=
σ
2
+
τ
2
{\displaystyle h_{\sigma }=h_{\tau }={\sqrt {\sigma ^{2}+\tau ^{2}}}}
因此,面積的無窮小元素是
d
A
=
(
σ
2
+
τ
2
)
d
σ
d
τ
{\displaystyle dA=\left(\sigma ^{2}+\tau ^{2}\right)d\sigma d\tau }
拉普拉斯算子 是
∇
2
Φ
=
1
σ
2
+
τ
2
(
∂
2
Φ
∂
σ
2
+
∂
2
Φ
∂
τ
2
)
{\displaystyle \nabla ^{2}\Phi ={\frac {1}{\sigma ^{2}+\tau ^{2}}}\left({\frac {\partial ^{2}\Phi }{\partial \sigma ^{2}}}+{\frac {\partial ^{2}\Phi }{\partial \tau ^{2}}}\right)}
其它微分算子,像
∇
⋅
F
{\displaystyle \nabla \cdot \mathbf {F} }
∇
×
F
{\displaystyle \nabla \times \mathbf {F} }
(
σ
,
τ
)
{\displaystyle (\sigma ,\ \tau )}
正交坐標系 條目內的一般公式。
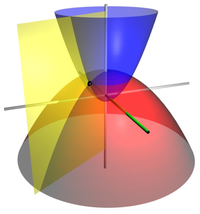
三維拋物線坐標的坐標曲面 。紅色的拋物曲面的坐標
τ
=
2
{\displaystyle \tau =2}
σ
=
1
{\displaystyle \sigma =1}
ϕ
=
−
60
∘
{\displaystyle \phi =-60^{\circ }}
P
=
(
1.0
,
−
1.732
,
1.5
)
{\displaystyle \mathbf {P} =(1.0,-1.732,1.5)}
將二維的拋物線坐標系繞著拋物線 的對稱軸旋轉,則可以得到三維的拋物線坐標系,又稱為旋轉拋物線坐標系 。將對稱軸與 z-軸排列成同直線;而拋物線坐標系的共焦點與直角坐標系的原點同地點。直角坐標
(
x
,
y
,
z
)
{\displaystyle (x,\ y,\ z)}
(
σ
,
τ
,
ϕ
)
{\displaystyle (\sigma ,\ \tau ,\ \phi )}
x
=
σ
τ
cos
ϕ
{\displaystyle x=\sigma \tau \cos \phi }
y
=
σ
τ
sin
ϕ
{\displaystyle y=\sigma \tau \sin \phi }
z
=
1
2
(
τ
2
−
σ
2
)
{\displaystyle z={\frac {1}{2}}\left(\tau ^{2}-\sigma ^{2}\right)}
其中,
σ
≥
0
{\displaystyle \sigma \geq 0}
τ
≥
0
{\displaystyle \tau \geq 0}
ϕ
{\displaystyle \phi }
tan
ϕ
=
y
x
,
0
≤
ϕ
≤
2
π
{\displaystyle \tan \phi ={\frac {y}{x}},\qquad 0\leq \phi \leq 2\pi }
反算回來,三維拋物線坐標
(
σ
,
τ
,
ϕ
)
{\displaystyle (\sigma ,\ \tau ,\ \phi )}
(
x
,
y
,
z
)
{\displaystyle (x,\ y,\ z)}
σ
=
−
z
+
x
2
+
y
2
+
z
2
{\displaystyle \sigma ={\sqrt {-z+{\sqrt {x^{2}+y^{2}+z^{2}}}}}}
τ
=
z
+
x
2
+
y
2
+
z
2
{\displaystyle \tau ={\sqrt {z+{\sqrt {x^{2}+y^{2}+z^{2}}}}}}
ϕ
=
tan
−
1
y
x
{\displaystyle \phi =\tan ^{-1}{\frac {y}{x}}}
每一個
σ
{\displaystyle \sigma }
拋物曲面 :
2
z
=
x
2
+
y
2
σ
2
−
σ
2
{\displaystyle 2z={\frac {x^{2}+y^{2}}{\sigma ^{2}}}-\sigma ^{2}}
而每一個
τ
{\displaystyle \tau }
拋物曲面 :
2
z
=
−
x
2
+
y
2
τ
2
+
τ
2
{\displaystyle 2z=-{\frac {x^{2}+y^{2}}{\tau ^{2}}}+\tau ^{2}}
這些拋物曲面的焦點的位置都在原點。
三維標度因子為:
h
σ
=
σ
2
+
τ
2
{\displaystyle h_{\sigma }={\sqrt {\sigma ^{2}+\tau ^{2}}}}
h
τ
=
σ
2
+
τ
2
{\displaystyle h_{\tau }={\sqrt {\sigma ^{2}+\tau ^{2}}}}
h
ϕ
=
σ
τ
{\displaystyle h_{\phi }=\sigma \tau \,}
我們可以觀察出,標度因子
h
σ
{\displaystyle h_{\sigma }}
h
τ
{\displaystyle h_{\tau }}
d
V
=
h
σ
h
τ
h
ϕ
=
σ
τ
(
σ
2
+
τ
2
)
d
σ
d
τ
d
ϕ
{\displaystyle dV=h_{\sigma }h_{\tau }h_{\phi }=\sigma \tau \left(\sigma ^{2}+\tau ^{2}\right)\,d\sigma \,d\tau \,d\phi }
拉普拉斯算子 是
∇
2
Φ
=
1
σ
2
+
τ
2
[
1
σ
∂
∂
σ
(
σ
∂
Φ
∂
σ
)
+
1
τ
∂
∂
τ
(
τ
∂
Φ
∂
τ
)
]
+
1
σ
2
τ
2
∂
2
Φ
∂
ϕ
2
{\displaystyle \nabla ^{2}\Phi ={\frac {1}{\sigma ^{2}+\tau ^{2}}}\left[{\frac {1}{\sigma }}{\frac {\partial }{\partial \sigma }}\left(\sigma {\frac {\partial \Phi }{\partial \sigma }}\right)+{\frac {1}{\tau }}{\frac {\partial }{\partial \tau }}\left(\tau {\frac {\partial \Phi }{\partial \tau }}\right)\right]+{\frac {1}{\sigma ^{2}\tau ^{2}}}{\frac {\partial ^{2}\Phi }{\partial \phi ^{2}}}}
其它微分算子,像
∇
⋅
F
{\displaystyle \nabla \cdot \mathbf {F} }
∇
×
F
{\displaystyle \nabla \times \mathbf {F} }
(
σ
,
τ
,
ϕ
)
{\displaystyle (\sigma ,\ \tau ,\ \phi )}
正交坐標系 條目內的一般公式。
另外還有一種拋物線坐標系的表述,專門用於哈密頓-亞可比方程式 。假若使用此種表述的公式,則哈密頓-亞可比方程式可以很容易的分解出來。應用此方法,可以導引出拉普拉斯-龍格-冷次向量 的恆定性.
採用下述從拋物線坐標變換至直角坐標的公式:
η
=
−
z
+
x
2
+
y
2
+
z
2
{\displaystyle \eta ={-z+{\sqrt {x^{2}+y^{2}+z^{2}}}}}
ξ
=
z
+
x
2
+
y
2
+
z
2
{\displaystyle \xi ={z+{\sqrt {x^{2}+y^{2}+z^{2}}}}}
ϕ
=
arctan
y
x
{\displaystyle \phi =\arctan {y \over x}}
假若
ϕ
=
0
{\displaystyle \phi =0}
x
≥
0
{\displaystyle x\geq 0}
η
=
−
z
+
x
2
+
z
2
{\displaystyle \eta =-z+{\sqrt {x^{2}+z^{2}}}}
ξ
=
z
+
x
2
+
z
2
{\displaystyle \xi =z+{\sqrt {x^{2}+z^{2}}}}
假若包含於一條曲線的每一點的坐標
η
{\displaystyle \eta }
η
=
c
{\displaystyle \eta =c}
z
|
η
=
c
=
x
2
2
c
−
c
2
{\displaystyle \left.z\right|_{\eta =c}={x^{2} \over 2c}-{c \over 2}}
這是一個共焦點在原點的拋物線;對稱軸與 z-軸同軸;凹性向上。
假若包含於一條曲線的每一點的坐標
ξ
{\displaystyle \xi }
ξ
=
b
{\displaystyle \xi =b}
z
|
ξ
=
b
=
b
2
−
x
2
2
b
{\displaystyle \left.z\right|_{\xi =b}={b \over 2}-{x^{2} \over 2b}}
這也是一個共焦點在原點的拋物線;對稱軸與 z-軸同軸;凹性向下。
思考任何一條向上的拋物線
η
=
c
{\displaystyle \eta =c}
ξ
=
b
{\displaystyle \xi =b}
x
2
2
c
−
c
2
=
b
2
−
x
2
2
b
{\displaystyle {x^{2} \over 2c}-{c \over 2}={b \over 2}-{x^{2} \over 2b}}
稍微計算,可得
x
=
b
c
{\displaystyle x={\sqrt {bc}}}
將相交點的横坐標
x
{\displaystyle x}
z
c
=
b
c
2
c
−
c
2
=
b
−
c
2
{\displaystyle z_{c}={bc \over 2c}-{c \over 2}={b-c \over 2}}
所以,相交點 P 坐標為
(
b
c
,
b
−
c
2
)
{\displaystyle \left({\sqrt {bc}},\ {b-c \over 2}\right)}
思考正切這兩條拋物線於點 P 的一對切線。向上的拋物線的切線的斜率為
d
z
c
d
x
=
x
c
=
b
c
=
s
c
{\displaystyle {\frac {dz_{c}}{dx}}={\frac {x}{c}}={\sqrt {\frac {b}{c}}}=s_{c}}
向下的拋物線的切線的斜率為
d
z
b
d
x
=
−
x
b
=
−
c
b
=
s
b
{\displaystyle {dz_{b} \over dx}=-{x \over b}=-{\sqrt {c \over b}}=s_{b}}
兩個斜率的乘積為
s
c
s
b
=
−
1
{\displaystyle s_{c}s_{b}=-1}
所以,兩條切線相垂直。對於任何兩條凹性相反的拋物線,都會有同樣的結果。
假設
ϕ
≠
0
{\displaystyle \phi \neq 0}
ϕ
{\displaystyle \phi }
0
{\displaystyle 0}
右手定則 旋轉;拋物線坐標為常數的拋物線 形成了拋物曲面。一對相反的拋物曲面的相交 設定了一個圓圈。而
ϕ
{\displaystyle \phi }
[ 1]
x
=
η
ξ
cos
ϕ
{\displaystyle x={\sqrt {\eta \xi }}\ \cos \phi }
y
=
η
ξ
sin
ϕ
{\displaystyle y={\sqrt {\eta \xi }}\ \sin \phi }
z
=
1
2
(
ξ
−
η
)
{\displaystyle z={\frac {1}{2}}(\xi -\eta )}
Morse PM, Feshbach H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill. 1953: p. 660. ISBN 0-07-043316-X . Margenau H, Murphy GM. The Mathematics of Physics and Chemistry. New York: D. van Nostrand. 1956: pp. 185–186. Korn GA, Korn TM. Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. 1961: p. 180. Sauer R, Szabó I. Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. 1967: p. 96. Zwillinger D. Handbook of Integration. Boston, MA: Jones and Bartlett. 1992: p. 114. ISBN 0-86720-293-9 Moon P, Spencer DE. Parabolic Coordinates (μ, ν, ψ). Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions corrected 2nd ed., 3rd print ed. New York: Springer-Verlag. 1988: pp. 34–36 (Table 1.08). ISBN 978-0387184302
^ Menzel, Donald H. Mathematical Physics. United States of America: Dover Publications. 1961: pp. 139. ISBN 978-0486600567(英语) .









































![{\displaystyle \nabla ^{2}\Phi ={\frac {1}{\sigma ^{2}+\tau ^{2}}}\left[{\frac {1}{\sigma }}{\frac {\partial }{\partial \sigma }}\left(\sigma {\frac {\partial \Phi }{\partial \sigma }}\right)+{\frac {1}{\tau }}{\frac {\partial }{\partial \tau }}\left(\tau {\frac {\partial \Phi }{\partial \tau }}\right)\right]+{\frac {1}{\sigma ^{2}\tau ^{2}}}{\frac {\partial ^{2}\Phi }{\partial \phi ^{2}}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/0de55bf6476e43e24c58491488f09964454617bd)

























