叉积

關於其他常稱作外積的相關二元運算，參閱外積 (消歧義)。

在数学和向量代数领域，叉積（英語：Cross product）又称向量积（英語：Vector product），是对三维空间中的两个向量的二元运算，使用符号 $\times$。与点积不同，它的运算结果是向量。对于线性无关的两个向量 $\mathbf {a}$ 和 $\mathbf {b}$，它们的叉积写作 $\mathbf {a} \times \mathbf {b}$，是 $\mathbf {a}$ 和 $\mathbf {b}$ 所在平面的法线向量，与 $\mathbf {a}$ 和 $\mathbf {b}$ 都垂直。叉积被广泛运用于数学、物理、工程学、计算机科学领域。

如果两个向量方向相同或相反（即它们非线性无关），亦或任意一个的长度为零，那么它们的叉积为零。推广开来，叉积的模长和以这两个向量为边的平行四边形的面积相等；如果两个向量成直角，它们叉积的模长即为两者长度的乘积。

叉积和点积一样依赖于欧几里德空间的度量，但与点积之不同的是，叉积还依赖于定向或右手定則。

在右手坐标系中的向量积

定义

使用右手定則确定叉积的方向

两个向量 $\mathbf {a}$ 和 $\mathbf {b}$ 的叉积仅在三维空间中有定义，写作 $\mathbf {a} \times \mathbf {b}$。在物理学中，叉积有时也被写成$\mathbf {a} \wedge \mathbf {b}$，但在数学中 $\mathbf {a} \wedge \mathbf {b}$ 是外代数中的外积。

叉积 $\mathbf {a} \times \mathbf {b}$ 是与 $\mathbf {a}$ 和 $\mathbf {b}$ 都垂直的向量 $\mathbf {c}$。其方向由右手定則决定，模长等于以两个向量为边的平行四边形的面积。

叉积可以定义为：

$\mathbf {a} \times \mathbf {b} =\|\mathbf {a} \|\|\mathbf {b} \|\sin(\theta )\ \mathbf {n}$

其中 $\theta$ 表示 $\mathbf {a}$ 和 $\mathbf {b}$ 在它们所定义的平面上的夹角（$0^{\circ }\leq \theta \leq 180^{\circ }$）。$\|\mathbf {a} \|$ 和 $\|\mathbf {b} \|$ 是向量 $\mathbf {a}$ 和 $\mathbf {b}$ 的模长，而 $\mathbf {n}$ 则是一个与 $\mathbf {a}$、$\mathbf {b}$ 所构成的平面垂直的单位向量，方向由右手定則决定。根据上述公式，当 $\mathbf {a}$ 与 $\mathbf {b}$ 平行（即 $\theta$ 为 0° 或 180°）时，它们的叉积为零向量 $\mathbf {0}$。

叉积a × b（垂直方向、紫色）随着向量 a（蓝色）和 b（红色）的夹角变化。 叉积垂直于两个向量，模长在两者平行时为零、在两者垂直时达到最大值‖a‖‖b‖。

按照惯例，向量 $\mathbf {n}$ 的方向由右手定則决定：将右手食指指向 $\mathbf {a}$ 的方向、中指指向 $\mathbf {b}$ 的方向，则此时拇指的方向即为 $\mathbf {n}$ 的方向。使用这一定则意味着叉积满足反交换律，$\mathbf {a} \times \mathbf {b} =-(\mathbf {b} \times \mathbf {a} )$：将右手食指指向 $\mathbf {b}$、中指指向 $\mathbf {a}$，那么拇指就必定指向相反方向，即翻转了叉积的符号。

由此可以看出，使用叉积需要考虑坐标系的利手性（英語：Handedness），如果使用的是左手坐标系，向量 $\mathbf {n}$ 的方向需要使用左手定则决定，与右手坐标系中的方向相反。

这样就会带来一个问题：参照系的变换不应该影响 $\mathbf {n}$ 的方向（例如从右手坐标系到左手坐标系的镜像变换）。因此，两个向量的叉积并不是（真）向量，而是伪向量。

计算

坐标表示

基向量（i、j、k，也记作 e₁、e₂、e₃）和向量 a 的分解（a_x、a_y、a_z，也记作 a₁、a₂、a₃)

右手坐标系中，基向量 $\mathbf {i}$、$\mathbf {j}$、$\mathbf {k}$ 满足以下等式：

${\begin{aligned}\mathbf {i} \times \mathbf {j} &=\mathbf {k} \\\mathbf {j} \times \mathbf {k} &=\mathbf {i} \\\mathbf {k} \times \mathbf {i} &=\mathbf {j} \end{aligned}}$

根据反交换律可以得出：

${\begin{aligned}\mathbf {j\times i} &=-\mathbf {k} \\\mathbf {k\times j} &=-\mathbf {i} \\\mathbf {i\times k} &=-\mathbf {j} \end{aligned}}$

根据叉积的定义可以得出：

$\mathbf {i} \times \mathbf {i} =\mathbf {j} \times \mathbf {j} =\mathbf {k} \times \mathbf {k} =\mathbf {0}$（零向量）。

根据以上等式，结合叉积的分配律和线性关系，就可以确定任意向量的叉积。

向量 $\mathbf {u}$ 和 $\mathbf {v}$ 可以定义为平行于基向量的三个正交元素之和：

${\begin{aligned}\mathbf {u} &=u_{1}\mathbf {i} +u_{2}\mathbf {j} +u_{3}\mathbf {k} \\\mathbf {v} &=v_{1}\mathbf {i} +v_{2}\mathbf {j} +v_{3}\mathbf {k} \end{aligned}}$

两者的叉积 $\mathbf {u} \times \mathbf {v}$ 可以根据分配律展开：

${\begin{aligned}\mathbf {u} \times \mathbf {v} ={}&(u_{1}\mathbf {i} +u_{2}\mathbf {j} +u_{3}\mathbf {k} )\times (v_{1}\mathbf {i} +v_{2}\mathbf {j} +v_{3}\mathbf {k} )\\={}&u_{1}v_{1}(\mathbf {i} \times \mathbf {i} )+u_{1}v_{2}(\mathbf {i} \times \mathbf {j} )+u_{1}v_{3}(\mathbf {i} \times \mathbf {k} )+{}\\&u_{2}v_{1}(\mathbf {j} \times \mathbf {i} )+u_{2}v_{2}(\mathbf {j} \times \mathbf {j} )+u_{2}v_{3}(\mathbf {j} \times \mathbf {k} )+{}\\&u_{3}v_{1}(\mathbf {k} \times \mathbf {i} )+u_{3}v_{2}(\mathbf {k} \times \mathbf {j} )+u_{3}v_{3}(\mathbf {k} \times \mathbf {k} )\\\end{aligned}}$

即把 $\mathbf {u} \times \mathbf {v}$ 分解为九个仅涉及 $\mathbf {i}$、$\mathbf {j}$、$\mathbf {k}$ 的简单叉积之和。九个叉积各自所涉及的向量，要么相互平行、要么相互正交。将最前面所述的几个等式带入其中，然后合并同类项，可以得到：

${\begin{aligned}\mathbf {u} \times \mathbf {v} ={}&-u_{1}v_{1}\mathbf {0} +u_{1}v_{2}\mathbf {k} -u_{1}v_{3}\mathbf {j} \\&-u_{2}v_{1}\mathbf {k} -u_{2}v_{2}\mathbf {0} +u_{2}v_{3}\mathbf {i} \\&+u_{3}v_{1}\mathbf {j} -u_{3}v_{2}\mathbf {i} -u_{3}v_{3}\mathbf {0} \\={}&(u_{2}v_{3}-u_{3}v_{2})\mathbf {i} +(u_{3}v_{1}-u_{1}v_{3})\mathbf {j} +(u_{1}v_{2}-u_{2}v_{1})\mathbf {k} \\\end{aligned}}$

即结果向量 $\mathbf {s} =s_{1}\mathbf {i} +s_{2}\mathbf {j} +s_{3}\mathbf {k} =\mathbf {u} \times \mathbf {v}$ 的三个标量元素为：

${\begin{aligned}s_{1}&=u_{2}v_{3}-u_{3}v_{2}\\s_{2}&=u_{3}v_{1}-u_{1}v_{3}\\s_{3}&=u_{1}v_{2}-u_{2}v_{1}\end{aligned}}$

也可以记作列向量的形式：

${\begin{pmatrix}s_{1}\\s_{2}\\s_{3}\end{pmatrix}}={\begin{pmatrix}u_{2}v_{3}-u_{3}v_{2}\\u_{3}v_{1}-u_{1}v_{3}\\u_{1}v_{2}-u_{2}v_{1}\end{pmatrix}}$

矩阵表示

根据萨吕法则确定 u 和 v 的叉积

叉积可以表达为这样的行列式：

$\mathbf {u\times v} ={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\u_{1}&u_{2}&u_{3}\\v_{1}&v_{2}&v_{3}\\\end{vmatrix}}$

这个行列式可以使用萨吕法则或拉普拉斯展开计算。使用萨吕法则可以展开为：

${\begin{aligned}\mathbf {u\times v} &=(u_{2}v_{3}\mathbf {i} +u_{3}v_{1}\mathbf {j} +u_{1}v_{2}\mathbf {k} )-(u_{3}v_{2}\mathbf {i} +u_{1}v_{3}\mathbf {j} +u_{2}v_{1}\mathbf {k} )\\&=(u_{2}v_{3}-u_{3}v_{2})\mathbf {i} +(u_{3}v_{1}-u_{1}v_{3})\mathbf {j} +(u_{1}v_{2}-u_{2}v_{1})\mathbf {k} \end{aligned}}$

使用拉普拉斯展开可以沿第一行展开为：

${\begin{aligned}\mathbf {u\times v} &={\begin{vmatrix}u_{2}&u_{3}\\v_{2}&v_{3}\end{vmatrix}}\mathbf {i} -{\begin{vmatrix}u_{1}&u_{3}\\v_{1}&v_{3}\end{vmatrix}}\mathbf {j} +{\begin{vmatrix}u_{1}&u_{2}\\v_{1}&v_{2}\end{vmatrix}}\mathbf {k} \\&=(u_{2}v_{3}-u_{3}v_{2})\mathbf {i} -(u_{1}v_{3}-u_{3}v_{1})\mathbf {j} +(u_{1}v_{2}-u_{2}v_{1})\mathbf {k} \end{aligned}}$

都可以直接得到结果向量。

性质

代数性质

對於任意三個向量 $\mathbf {a}$、$\mathbf {b}$、$\mathbf {c}$，

• $\mathbf {a} \times \mathbf {a} =\mathbf {0}$
• $\mathbf {a} \times \mathbf {0} =\mathbf {0}$
• $\mathbf {a} \times \mathbf {b} =-(\mathbf {b} \times \mathbf {a} )$（反交换律）
• $\mathbf {a} \times (\mathbf {b} +\mathbf {c} )=\mathbf {a} \times \mathbf {b} +\mathbf {a} \times \mathbf {c}$（加法的左分配律）
• $(\mathbf {a} +\mathbf {b} )\times \mathbf {c} =\mathbf {a} \times \mathbf {c} +\mathbf {b} \times \mathbf {c}$（加法的右分配律）
• $(\lambda \mathbf {a} )\times \mathbf {b} =\lambda (\mathbf {a} \times \mathbf {b} )=\mathbf {a} \times (\lambda \mathbf {b} )$
• $\mathbf {a} \times \mathbf {b} +\mathbf {c} \times \mathbf {d} =(\mathbf {a} -\mathbf {c} )\times (\mathbf {b} -\mathbf {d} )+\mathbf {a} \times \mathbf {d} +\mathbf {c} \times \mathbf {b}$
• $|\mathbf {a} \times \mathbf {b} |=|\mathbf {b} \times \mathbf {a} |$
• $|\mathbf {a} \times \mathbf {b} |^{2}=|\mathbf {a} |^{2}|\mathbf {b} |^{2}-(\mathbf {a} \cdot \mathbf {b} )^{2}={\begin{vmatrix}\mathbf {a} \cdot \mathbf {a} &\mathbf {a} \cdot \mathbf {b} \\\mathbf {a} \cdot \mathbf {b} &\mathbf {b} \cdot \mathbf {b} \\\end{vmatrix}}$（拉格朗日恆等式）

一般來說，向量叉積不遵守約簡律，即 $\mathbf {a} \times \mathbf {b} =\mathbf {a} \times \mathbf {c}$ 不表示 $\mathbf {b} =\mathbf {c}$。此外，$\mathbf {a} \times \mathbf {b} =\mathbf {0}$ 不表示 $\mathbf {a} =\mathbf {0}$ 或 $\mathbf {b} =\mathbf {0}$。

但對於两个非零向量 $\mathbf {a}$ 和 $\mathbf {b}$，

• $\mathbf {a} \times \mathbf {b} =\mathbf {0}$ 當且僅當 $\mathbf {a}$ 平行於 $\mathbf {b}$

三重積

主条目：三重積

純量三重積满足以下特殊的结合律：

• $\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )=(\mathbf {a} \times \mathbf {b} )\cdot \mathbf {c}$

向量三重積不满足结合律，但满足以下恆等式：

• $\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )\;+\mathbf {b} \times (\mathbf {c} \times \mathbf {a} )\;+\mathbf {c} \times (\mathbf {a} \times \mathbf {b} )=\mathbf {0}$ （雅可比恆等式）

向量三重積亦可以點積展開：

• $\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )$（拉格朗日公式）

向量微分

對於實數 $t$ 和兩個向量值函數 $\mathbf {a} (t)$、$\mathbf {b} (t)$，乘積法則成立：

• ${\frac {d}{dt}}(\mathbf {a} \times \mathbf {b} )={\frac {d\mathbf {a} }{dt}}\times \mathbf {b} +\mathbf {a} \times {\frac {d\mathbf {b} }{dt}}$

三維坐標

给定直角坐标系的单位向量$\mathbf {i}$，$\mathbf {j}$，$\mathbf {k}$满足下列等式：

$\mathbf {i} \times \mathbf {j} =\mathbf {k}$、$\mathbf {j} \times \mathbf {k} =\mathbf {i}$、$\mathbf {k} \times \mathbf {i} =\mathbf {j}$

通过这些规则，两个向量的叉积的坐标可以方便地计算出来，不需要考虑任何角度：设

$\mathbf {a} =a_{1}\mathbf {i} +a_{2}\mathbf {j} +a_{3}\mathbf {k}$

$\mathbf {b} =b_{1}\mathbf {i} +b_{2}\mathbf {j} +b_{3}\mathbf {k}$

则

${\begin{aligned}\mathbf {a} \times \mathbf {b} &=(a_{2}b_{3}-a_{3}b_{2})\mathbf {i} +(a_{3}b_{1}-a_{1}b_{3})\mathbf {j} +(a_{1}b_{2}-a_{2}b_{1})\mathbf {k} \\&={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\\end{vmatrix}}\end{aligned}}$

叉积也可以用四元数来表示。注意到上述 $\mathbf {i}$、$\mathbf {j}$、$\mathbf {k}$ 之间的叉积满足四元数的乘法。一般而言，若将向量[a₁, a₂, a₃]表示成四元数a₁i + a₂j + a₃k，两个向量的叉积可以这样计算：计算两个四元数的乘积得到一个四元数，并将这个四元数的实部去掉，即为结果。更多关于四元数乘法，向量运算及其几何意义请参见四元数与空间旋转。

几何意义

以向量定義的平行四边形。

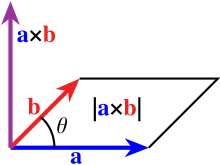
由向量 $\mathbf {a}$ 和 $\mathbf {b}$ 定義兩條鄰邊的平行四边形，其面積 $A$ 為

$A=|\mathbf {a} ||\mathbf {b} |\sin \theta$

因此兩支向量叉積的模長可視作平行四边形其面積：

• $A=|\mathbf {a} \times \mathbf {b} |$

高维情形

七维向量的叉积可以通过八元数得到，与上述的四元数方法相同。

七维叉积具有与三维叉积相似的性质：

• 双线性性：

$\mathbf {x} \times (a\mathbf {y} +b\mathbf {z} )=a\mathbf {x} \times \mathbf {y} +b\mathbf {x} \times \mathbf {z}$

$(a\mathbf {y} +b\mathbf {z} )\times \mathbf {x} =a\mathbf {y} \times \mathbf {x} +b\mathbf {z} \times \mathbf {x}$

• 反交换律：

$\mathbf {x} \times \mathbf {y} +\mathbf {y} \times \mathbf {x} =\mathbf {0}$

• $\mathbf {x} \times \mathbf {y}$ 同时与 $\mathbf {x}$ 和 $\mathbf {y}$ 垂直：

$\mathbf {x} \cdot (\mathbf {x} \times \mathbf {y} )=\mathbf {y} \cdot (\mathbf {x} \times \mathbf {y} )=\mathbf {0}$

• 拉格朗日恒等式：

$|\mathbf {x} \times \mathbf {y} |^{2}=|\mathbf {x} |^{2}|\mathbf {y} |^{2}-(\mathbf {x} \cdot \mathbf {y} )^{2}$

• 不同于三维情形，它并不满足雅可比恒等式：

$\mathbf {x} \times (\mathbf {y} \times \mathbf {z} )\;+\mathbf {y} \times (\mathbf {z} \times \mathbf {x} )\;+\mathbf {z} \times (\mathbf {x} \times \mathbf {y} )\neq \mathbf {0}$

应用

另外，在物理学力学、电磁学、光学和计算机图形学等理工学科中，叉积应用十分广泛。例如力矩、角动量、洛伦兹力等矢量都可以由向量的叉积求解。在进行这些物理量的计算时，往往可以借助右手定则辅助判断方向。

参见

• 純量积
• 三重積
• 右手定则
• 外代数：叉乘的实质，赝矢量与赝标量