散度

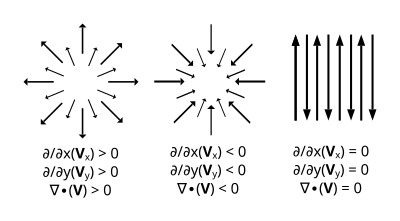
不同的向量场的散度。向量场自点(x,y)的散度等于它在这个点上的x分量关于x的偏导数与y分量关于y的偏导数的和： $\nabla \!\cdot (\mathbf {V} (x,y))={\frac {\partial \ {\mathbf {V} _{x}(x,y)}}{\partial {x}}}+{\frac {\partial \ {\mathbf {V} _{y}(x,y)}}{\partial {y}}}$

散度或稱發散度，是向量分析中的一个向量算子，将向量空间上的一个向量场（矢量场）对应到一个标量场上。散度描述的是向量场里一个点是汇聚点还是发源点，形象地说，就是这包含这一点的一个微小体元中的向量是“向外”居多还是“向内”居多。举例来说，考虑空间中的静电场，其空间里的电场强度是一个矢量场。正电荷附近，电场线“向外”发射，所以正电荷处的散度为正值，电荷越大，散度越大。负电荷附近，电场线“向内”，所以负电荷处的散度为负值，电荷越大，散度越小。向量函數的散度為一個純量，而二阶张量的散度是向量函数。

定义

定义向量场的散度，首先要引入通量的概念。给定一个三维空间中的向量场$\mathbf {A}$以及一个简单有向曲面$\Sigma$，则向量场$\mathbf {A}$通过曲面$\Sigma$的通量就是曲面每一点$x$上的场向量$\mathbf {A} (x)$在曲面法向方向上的分量的积分:

$\Phi _{\mathbf {A} }(\Sigma )=\iint \limits _{\Sigma }\mathbf {A} \cdot \mathbf {n} \mathrm {d} S$

其中$\mathrm {d} S$是积分的面积元，n是Σ在点(x,y,z)处的单位法向量。如果曲面是封闭的，例如球面，那么通常约定法向量是从裡朝外的，所以这时候的通量是描述曲面上的场向量朝外的程度。

通量描述了一固定区域（也就是 $\Sigma$ ）上向量场的流通傾向，散度在某點的值则是这个性质的在這點的局部描述，也就是说，从散度在一点的值，我们可以看出向量场在这点附近到底倾向发散还是收敛。要算某一点 $x$ 的散度，先求包含这一点的某一个封闭曲面 $\Sigma$ 的通量 $\Phi _{\mathbf {A} }(\Sigma )$ 除以封闭曲面 $\Sigma$ 围起来的微小体元 $\delta V$ 的体积 （这个体积用 $|\delta V|$ 表示） 得到的比值，矢量场 $\mathbf {A}$ 在点 $x$ 的散度即是这个比值在体积微元 $\delta V$ 趋向于点 $x$ 时的极限。用数学公式表示即：

$\operatorname {div} \mathbf {A} (x)=\lim _{\delta V\rightarrow \{x\}}\oint _{\Sigma }{\mathbf {A} \cdot \mathbf {n} \over |\delta V|}\;dS=\lim _{\delta V\rightarrow \{x\}}{\frac {\Phi _{\mathbf {A} }(\Sigma )}{|\delta V|}}$

如果用Nabla算子 $\nabla$ 表示的话，向量场 $\mathbf {A}$ 的散度记作：$\operatorname {div} \,\mathbf {A} =\nabla \cdot \mathbf {A} .$

物理意义

从定义中可以看出，散度是向量场的一种强度性质，就如同密度、浓度、温度一样，它对应的广延性质是一个封闭区域表面的通量，所以说散度是通量的体密度。下面从散度的极限表达式来看它的物理意义。

设${\textstyle \mathbf {P} }$为场域V中的一点，现作包围${\textstyle \mathbf {P} }$点的任一闭合曲面${\textstyle \mathbf {S} }$，$\Delta V$是S面所围的区域。那么：$$\oint _{S}{\mathbf {A} \cdot d\mathbf {S} }=\iiint \limits _{\Delta V}\mathrm {div} \mathbf {A} dV\;\;\;\;(1)$$

利用中值定理得$$\iiint \limits _{\Delta V}\mathrm {div} \mathbf {A} dV=\mathrm {(} \mathrm {div} \mathbf {A} \mathrm {)} _{x}\cdot |\Delta V|\;\;\;\;(2)$$

式中 $x$ 为 $\Delta V$中的某一点，$|\Delta V|$ 為 $\Delta V$ 的體積。带入(1)中后得$$\mathrm {(} \mathrm {div} \mathbf {A} \mathrm {)} _{x}={\frac {1}{|\Delta V|}}\oint _{S}{\mathbf {A} \cdot d\mathbf {S} }$$

令$\Delta V$向点P收缩，则 $x$ 点就趋向于P点，所以在P点的散度可由下列极限表示$$(\mathrm {div} \mathbf {A} )_{P}=\lim _{\Delta V\rightarrow P}{\frac {1}{|\Delta V|}}\oint _{S}{\mathbf {A} \cdot d\mathbf {S} }$$

若在上式中令${\textstyle \Delta \Phi =\oint _{S}{\mathbf {A} \cdot d\mathbf {S} }}$,那么

$$(\mathrm {div} \mathbf {A} )_{P}=\lim _{\Delta V\rightarrow P}{\frac {1}{|\Delta V|}}\oint _{S}{\mathbf {A} \cdot d\mathbf {S} }=\lim _{\Delta V\rightarrow P}{\frac {\Delta \Phi }{|\Delta V|}}={\frac {d\Phi }{dV}}$$

由此可见，散度是通量${\textstyle \Phi }$对曲面所围区域体積的变化率，也可看成通量在V中的分布密度。所以${\textstyle \mathrm {div} \mathbf {A} }$也称为通量密度。

物理上，散度的意义是场的有源性。某一点或某个区域的散度大于零，表示向量场在这一点或这一区域有新的通量产生，小于零则表示向量场在这一点或区域有通量湮灭。这样的点或区域分别称为向量场的正源（发散源）和负源（洞）。举例来说，假设将太空中各个点的热辐射强度向量看做一个向量场，那么某个热辐射源（比如太阳）周边的热辐射强度向量都指向外，说明太阳是不断产生新的热辐射的源头，其散度大于零。

散度等于零的区域称为无源场或管形场。流体力学中，散度为零的流体称为不可压缩流体，也就是说此流体中不会有一部分凭空消失或突然产生，每个微小时间间隔中流入一个微小体元的流体总量都等于在此时间间隔内流出此体元的流体总量。

分量表示

在不同的坐标系下，向量场的散度有不同的表达方式。

直角坐标系

在三维直角坐标系 $xyz$ 中，设向量场 $\mathbf {A}$ 的表示为：

$\mathbf {A} (x,y,z)=A_{x}(x,y,z)\mathbf {i} +A_{y}(x,y,z)\mathbf {j} +A_{z}(x,y,z)\mathbf {k}$，

其中的 $\mathbf {i} ,\mathbf {j} ,\mathbf {k}$ 分别是 $x$轴、$y$轴、$z$轴方向上的单位向量，场的分量 $A_{x},A_{y},A_{z}$ 具有一阶连续偏导数，那么向量场 $\mathbf {A}$ 的散度就是：

$\operatorname {div} \mathbf {A} =\nabla \cdot \mathbf {A} ={\frac {\partial A_{x}}{\partial x}}+{\frac {\partial A_{y}}{\partial y}}+{\frac {\partial A_{z}}{\partial z}}$

圆柱坐标系

圆柱坐标系中，假设物体的位置为$(r,\varphi ,z)$，定义其径向单位矢量、横向单位矢量和纵向单位矢量为${\boldsymbol {e}}_{r},{\boldsymbol {e}}_{\varphi },{\boldsymbol {e}}_{z}$，那么向量场$\mathbf {A}$可以表示成：

$\mathbf {A} =A_{r}(r,\varphi ,z){\boldsymbol {e}}_{r}+A_{z}(r,\varphi ,z){\boldsymbol {e}}_{z}+A_{\varphi }(r,\varphi ,z){\boldsymbol {e}}_{\varphi },$

向量场A的散度就是：

$\operatorname {div} \,\mathbf {A} =\nabla \cdot \mathbf {A} ={\frac {1}{r}}{\frac {\partial }{\partial r}}(rA_{r})+{\frac {1}{r}}{\frac {\partial A_{\varphi }}{\partial \varphi }}+{\frac {\partial A_{z}}{\partial z}}\,.$

球坐标系

球坐标系中，假设物体的位置用球坐标表示为$(r,\theta ,\varphi )$，定义它的基矢：${\boldsymbol {e}}_{r},{\boldsymbol {e}}_{\theta },{\boldsymbol {e}}_{\varphi }$，则向量场A可以表示成：

$\mathbf {A} =A_{r}(r,\theta ,\varphi ){\boldsymbol {e}}_{r}+A_{\theta }(r,\theta ,\varphi ){\boldsymbol {e}}_{\theta }+A_{\varphi }(r,\theta ,\varphi ){\boldsymbol {e}}_{\varphi },$

向量场A的散度就是：

$\operatorname {div} \,\mathbf {A} =\nabla \cdot \mathbf {A} ={\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}(r^{2}A_{r})+{\frac {1}{r\sin \theta }}{\frac {\partial }{\partial \theta }}(\sin \theta \,A_{\theta })+{\frac {1}{r\sin \theta }}{\frac {\partial A_{\varphi }}{\partial \varphi }}.$

性质

以下的性质都可以从常见的求导法则推出。最重要的是，散度是一个线性算子，也就是说：

$\operatorname {div} (a\mathbf {F} +b\mathbf {G} )=a\;\operatorname {div} (\mathbf {F} )+b\;\operatorname {div} (\mathbf {G} )$

其中F和G是向量场，a和b是实数。

设$\varphi$是标量函数，F是向量场，则它们的乘积的散度为：

$\operatorname {div} (\varphi \mathbf {F} )=\operatorname {grad} (\varphi )\cdot \mathbf {F} +\varphi \;\operatorname {div} (\mathbf {F} ),$ 或 $\nabla \cdot (\varphi \mathbf {F} )=(\nabla \varphi )\cdot \mathbf {F} +\varphi \;(\nabla \cdot \mathbf {F} ).$

设有两个向量场F和G，则它们的向量积的散度为：

$\operatorname {div} (\mathbf {F} \times \mathbf {G} )=\operatorname {curl} (\mathbf {F} )\cdot \mathbf {G} \;-\;\mathbf {F} \cdot \operatorname {curl} (\mathbf {G} ),$ 或 $\nabla \cdot (\mathbf {F} \times \mathbf {G} )=(\nabla \times \mathbf {F} )\cdot \mathbf {G} -\mathbf {F} \cdot (\nabla \times \mathbf {G} ).$

其中$\operatorname {curl}$是旋度。

对一个标量场求梯度后再求散度，等于拉普拉斯算子作用在其上：

$\operatorname {div} \,\operatorname {grad} f=\nabla \cdot \nabla f=\Delta f$ (在 $\mathbb {R} ^{n}$ 的向量分析中 $\nabla \cdot \nabla f$ 也寫作 $\nabla ^{2}f)$。

高斯散度定理

主条目：高斯散度定理

既然向量场某一处的散度是向量场在该处附近通量的体密度，那么对某一个体积内的散度进行积分，就应该得到这个体积内的总通量。事实上可以证明这个推论是正确的，称为高斯散度定理。高斯定理说明，如果在体积V内的向量场A拥有散度，那么散度的体积分等于向量场在V的表面S的面积分：

$\iiint \limits _{V}\mathrm {div} \mathbf {A} dv=\int \!\!\!\!\int _{S}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\;\;\;\bigcirc \,\,\mathbf {A} \cdot \mathbf {n} dS$

历史

作为向量分析的基础概念，散度同样源自对四元数上的微积分研究。哈密顿在介绍四元数的运算时，将一个四元数$q=A+B{\boldsymbol {i}}+C{\boldsymbol {j}}+D{\boldsymbol {k}}$中的$A$称为“标量部分”（scalar part），将$B{\boldsymbol {i}}+C{\boldsymbol {j}}+D{\boldsymbol {k}}$称为“向量部分”（vector part）。他引入了四元数的偏微分算子$\nabla ={\boldsymbol {i}}{\frac {\mathrm {d} }{\mathrm {d} x}}+{\boldsymbol {j}}{\frac {\mathrm {d} }{\mathrm {d} y}}+{\boldsymbol {k}}{\frac {\mathrm {d} }{\mathrm {d} z}}$（即$\nabla$算子）后，计算$\nabla$对一个四元数之向量部分$\sigma =B{\boldsymbol {i}}+C{\boldsymbol {j}}+D{\boldsymbol {k}}$的效果：

$\nabla \sigma =({\boldsymbol {i}}{\frac {\mathrm {d} }{\mathrm {d} x}}+{\boldsymbol {j}}{\frac {\mathrm {d} }{\mathrm {d} y}}+{\boldsymbol {k}}{\frac {\mathrm {d} }{\mathrm {d} z}})(B{\boldsymbol {i}}+C{\boldsymbol {j}}+D{\boldsymbol {k}})$

$=-\left({\frac {\mathrm {d} B}{\mathrm {d} x}}+{\frac {\mathrm {d} C}{\mathrm {d} y}}+{\frac {\mathrm {d} D}{\mathrm {d} z}}\right)+\left(\left({\frac {\mathrm {d} D}{\mathrm {d} y}}-{\frac {\mathrm {d} C}{\mathrm {d} z}}\right){\boldsymbol {i}}+\left({\frac {\mathrm {d} B}{\mathrm {d} z}}-{\frac {\mathrm {d} D}{\mathrm {d} x}}\right){\boldsymbol {j}}+\left({\frac {\mathrm {d} C}{\mathrm {d} x}}-{\frac {\mathrm {d} B}{\mathrm {d} y}}\right){\boldsymbol {k}}\right)$

麦克斯韦在1873年的论文中将其中的“标量部分”：$-\left({\frac {\mathrm {d} B}{\mathrm {d} x}}+{\frac {\mathrm {d} C}{\mathrm {d} y}}+{\frac {\mathrm {d} D}{\mathrm {d} z}}\right)$称为“聚集度”（Convergence），而将“向量部分”：$\left({\frac {\mathrm {d} D}{\mathrm {d} y}}-{\frac {\mathrm {d} C}{\mathrm {d} z}}\right){\boldsymbol {i}}+\left({\frac {\mathrm {d} B}{\mathrm {d} z}}-{\frac {\mathrm {d} D}{\mathrm {d} x}}\right){\boldsymbol {j}}+\left({\frac {\mathrm {d} C}{\mathrm {d} x}}-{\frac {\mathrm {d} B}{\mathrm {d} y}}\right){\boldsymbol {k}}$称为“旋度”（Curl）或“变度”（Version）。亥维赛在1883年发表的论文：《电学与磁学中的若干关系》（Some Electrostatic and Magnetic Relations）中讨论了静电场中电场力的聚集度。他计算出在电荷体密度为$\rho$的一点上，有：$4\pi \rho =-\operatorname {conv} \,R={\frac {\mathrm {d} R_{x}}{\mathrm {d} x}}+{\frac {\mathrm {d} R_{y}}{\mathrm {d} y}}+{\frac {\mathrm {d} R_{z}}{\mathrm {d} z}}.\,$其中$R$是电场力。他将这个关系解释为电荷的存在是电场力汇聚的相反。如果将聚集度解释为电场力进入一个微小体积的总和，那么加上一个负号之后，就可以描述一个微小体积中散发出的电场力总和，他将其称为“散度”（divergence）。他认为有必要将$\nabla$算子对一个四元数$q$的作用效果分开，并将$\nabla q$的向量部分分成散度部分$\operatorname {div} \,q$和旋度部分$\operatorname {curl} \,q$ 。

参阅

• 旋度
• 梯度
• 高斯散度定理