散度

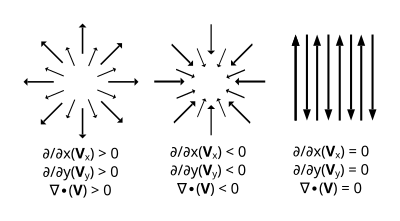
不同的向量場的散度。向量場自點(x,y)的散度等於它在這個點上的x分量關於x的偏導數與y分量關於y的偏導數的和： $\nabla \!\cdot (\mathbf {V} (x,y))={\frac {\partial \ {\mathbf {V} _{x}(x,y)}}{\partial {x}}}+{\frac {\partial \ {\mathbf {V} _{y}(x,y)}}{\partial {y}}}$

散度或稱發散度，是向量分析中的一個向量算子，將向量空間上的一個向量場（矢量場）對應到一個純量場上。散度描述的是向量場裡一個點是匯聚點還是發源點，形象地說，就是這包含這一點的一個微小體元中的向量是「向外」居多還是「向內」居多。舉例來說，考慮空間中的靜電場，其空間裡的電場強度是一個矢量場。正電荷附近，電場線「向外」發射，所以正電荷處的散度為正值，電荷越大，散度越大。負電荷附近，電場線「向內」，所以負電荷處的散度為負值，電荷越大，散度越小。向量函數的散度為一個純量，而二階張量的散度是向量函數。

定義

定義向量場的散度，首先要引入通量的概念。給定一個三維空間中的向量場$\mathbf {A}$以及一個簡單有向曲面$\Sigma$，則向量場$\mathbf {A}$通過曲面$\Sigma$的通量就是曲面每一點$x$上的場向量$\mathbf {A} (x)$在曲面法向方向上的分量的積分:

$\Phi _{\mathbf {A} }(\Sigma )=\iint \limits _{\Sigma }\mathbf {A} \cdot \mathbf {n} \mathrm {d} S$

其中$\mathrm {d} S$是積分的面積元，n是Σ在點(x,y,z)處的單位法向量。如果曲面是封閉的，例如球面，那麼通常約定法向量是從裡朝外的，所以這時候的通量是描述曲面上的場向量朝外的程度。

通量描述了一固定區域（也就是 $\Sigma$ ）上向量場的流通傾向，散度在某點的值則是這個性質的在這點的局部描述，也就是說，從散度在一點的值，我們可以看出向量場在這點附近到底傾向發散還是收斂。要算某一點 $x$ 的散度，先求包含這一點的某一個封閉曲面 $\Sigma$ 的通量 $\Phi _{\mathbf {A} }(\Sigma )$ 除以封閉曲面 $\Sigma$ 圍起來的微小體元 $\delta V$ 的體積 （這個體積用 $|\delta V|$ 表示） 得到的比值，矢量場 $\mathbf {A}$ 在點 $x$ 的散度即是這個比值在體積微元 $\delta V$ 趨向於點 $x$ 時的極限。用數學公式表示即：

$\operatorname {div} \mathbf {A} (x)=\lim _{\delta V\rightarrow \{x\}}\oint _{\Sigma }{\mathbf {A} \cdot \mathbf {n} \over |\delta V|}\;dS=\lim _{\delta V\rightarrow \{x\}}{\frac {\Phi _{\mathbf {A} }(\Sigma )}{|\delta V|}}$

如果用Nabla算子 $\nabla$ 表示的話，向量場 $\mathbf {A}$ 的散度記作：$\operatorname {div} \,\mathbf {A} =\nabla \cdot \mathbf {A} .$

物理意義

從定義中可以看出，散度是向量場的一種強度性質，就如同密度、濃度、溫度一樣，它對應的廣延性質是一個封閉區域表面的通量，所以說散度是通量的體密度。下面從散度的極限表達式來看它的物理意義。

設${\textstyle \mathbf {P} }$為場域V中的一點，現作包圍${\textstyle \mathbf {P} }$點的任一閉合曲面${\textstyle \mathbf {S} }$，$\Delta V$是S面所圍的區域。那麼：$$\oint _{S}{\mathbf {A} \cdot d\mathbf {S} }=\iiint \limits _{\Delta V}\mathrm {div} \mathbf {A} dV\;\;\;\;(1)$$

利用均值定理得$$\iiint \limits _{\Delta V}\mathrm {div} \mathbf {A} dV=\mathrm {(} \mathrm {div} \mathbf {A} \mathrm {)} _{x}\cdot |\Delta V|\;\;\;\;(2)$$

式中 $x$ 為 $\Delta V$中的某一點，$|\Delta V|$ 為 $\Delta V$ 的體積。帶入(1)中後得$$\mathrm {(} \mathrm {div} \mathbf {A} \mathrm {)} _{x}={\frac {1}{|\Delta V|}}\oint _{S}{\mathbf {A} \cdot d\mathbf {S} }$$

令$\Delta V$向點P收縮，則 $x$ 點就趨向於P點，所以在P點的散度可由下列極限表示$$(\mathrm {div} \mathbf {A} )_{P}=\lim _{\Delta V\rightarrow P}{\frac {1}{|\Delta V|}}\oint _{S}{\mathbf {A} \cdot d\mathbf {S} }$$

若在上式中令${\textstyle \Delta \Phi =\oint _{S}{\mathbf {A} \cdot d\mathbf {S} }}$,那麼

$$(\mathrm {div} \mathbf {A} )_{P}=\lim _{\Delta V\rightarrow P}{\frac {1}{|\Delta V|}}\oint _{S}{\mathbf {A} \cdot d\mathbf {S} }=\lim _{\Delta V\rightarrow P}{\frac {\Delta \Phi }{|\Delta V|}}={\frac {d\Phi }{dV}}$$

由此可見，散度是通量${\textstyle \Phi }$對曲面所圍區域體積的變化率，也可看成通量在V中的分布密度。所以${\textstyle \mathrm {div} \mathbf {A} }$也稱為通量密度。

物理上，散度的意義是場的有源性。某一點或某個區域的散度大於零，表示向量場在這一點或這一區域有新的通量產生，小於零則表示向量場在這一點或區域有通量湮滅。這樣的點或區域分別稱為向量場的正源（發散源）和負源（洞）。舉例來說，假設將太空中各個點的熱輻射強度向量看做一個向量場，那麼某個熱輻射源（比如太陽）周邊的熱輻射強度向量都指向外，說明太陽是不斷產生新的熱輻射的源頭，其散度大於零。

散度等於零的區域稱為無源場或管形場。流體力學中，散度為零的流體稱為不可壓縮流體，也就是說此流體中不會有一部分憑空消失或突然產生，每個微小時間間隔中流入一個微小體元的流體總量都等於在此時間間隔內流出此體元的流體總量。

分量表示

在不同的坐標系下，向量場的散度有不同的表達方式。

直角坐標系

在三維直角坐標系 $xyz$ 中，設向量場 $\mathbf {A}$ 的表示為：

$\mathbf {A} (x,y,z)=A_{x}(x,y,z)\mathbf {i} +A_{y}(x,y,z)\mathbf {j} +A_{z}(x,y,z)\mathbf {k}$，

其中的 $\mathbf {i} ,\mathbf {j} ,\mathbf {k}$ 分別是 $x$軸、$y$軸、$z$軸方向上的單位向量，場的分量 $A_{x},A_{y},A_{z}$ 具有一階連續偏導數，那麼向量場 $\mathbf {A}$ 的散度就是：

$\operatorname {div} \mathbf {A} =\nabla \cdot \mathbf {A} ={\frac {\partial A_{x}}{\partial x}}+{\frac {\partial A_{y}}{\partial y}}+{\frac {\partial A_{z}}{\partial z}}$

圓柱坐標系

圓柱坐標系中，假設物體的位置為$(r,\varphi ,z)$，定義其徑向單位矢量、橫向單位矢量和縱向單位矢量為${\boldsymbol {e}}_{r},{\boldsymbol {e}}_{\varphi },{\boldsymbol {e}}_{z}$，那麼向量場$\mathbf {A}$可以表示成：

$\mathbf {A} =A_{r}(r,\varphi ,z){\boldsymbol {e}}_{r}+A_{z}(r,\varphi ,z){\boldsymbol {e}}_{z}+A_{\varphi }(r,\varphi ,z){\boldsymbol {e}}_{\varphi },$

向量場A的散度就是：

$\operatorname {div} \,\mathbf {A} =\nabla \cdot \mathbf {A} ={\frac {1}{r}}{\frac {\partial }{\partial r}}(rA_{r})+{\frac {1}{r}}{\frac {\partial A_{\varphi }}{\partial \varphi }}+{\frac {\partial A_{z}}{\partial z}}\,.$

球坐標系

球坐標系中，假設物體的位置用球坐標表示為$(r,\theta ,\varphi )$，定義它的基矢：${\boldsymbol {e}}_{r},{\boldsymbol {e}}_{\theta },{\boldsymbol {e}}_{\varphi }$，則向量場A可以表示成：

$\mathbf {A} =A_{r}(r,\theta ,\varphi ){\boldsymbol {e}}_{r}+A_{\theta }(r,\theta ,\varphi ){\boldsymbol {e}}_{\theta }+A_{\varphi }(r,\theta ,\varphi ){\boldsymbol {e}}_{\varphi },$

向量場A的散度就是：

$\operatorname {div} \,\mathbf {A} =\nabla \cdot \mathbf {A} ={\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}(r^{2}A_{r})+{\frac {1}{r\sin \theta }}{\frac {\partial }{\partial \theta }}(\sin \theta \,A_{\theta })+{\frac {1}{r\sin \theta }}{\frac {\partial A_{\varphi }}{\partial \varphi }}.$

性質

以下的性質都可以從常見的求導法則推出。最重要的是，散度是一個線性算子，也就是說：

$\operatorname {div} (a\mathbf {F} +b\mathbf {G} )=a\;\operatorname {div} (\mathbf {F} )+b\;\operatorname {div} (\mathbf {G} )$

其中F和G是向量場，a和b是實數。

設$\varphi$是純量函數，F是向量場，則它們的乘積的散度為：

$\operatorname {div} (\varphi \mathbf {F} )=\operatorname {grad} (\varphi )\cdot \mathbf {F} +\varphi \;\operatorname {div} (\mathbf {F} ),$ 或 $\nabla \cdot (\varphi \mathbf {F} )=(\nabla \varphi )\cdot \mathbf {F} +\varphi \;(\nabla \cdot \mathbf {F} ).$

設有兩個向量場F和G，則它們的向量積的散度為：

$\operatorname {div} (\mathbf {F} \times \mathbf {G} )=\operatorname {curl} (\mathbf {F} )\cdot \mathbf {G} \;-\;\mathbf {F} \cdot \operatorname {curl} (\mathbf {G} ),$ 或 $\nabla \cdot (\mathbf {F} \times \mathbf {G} )=(\nabla \times \mathbf {F} )\cdot \mathbf {G} -\mathbf {F} \cdot (\nabla \times \mathbf {G} ).$

其中$\operatorname {curl}$是旋度。

對一個純量場求梯度後再求散度，等於拉普拉斯算子作用在其上：

$\operatorname {div} \,\operatorname {grad} f=\nabla \cdot \nabla f=\Delta f$ (在 $\mathbb {R} ^{n}$ 的向量分析中 $\nabla \cdot \nabla f$ 也寫作 $\nabla ^{2}f)$。

高斯散度定理

主條目：高斯散度定理

既然向量場某一處的散度是向量場在該處附近通量的體密度，那麼對某一個體積內的散度進行積分，就應該得到這個體積內的總通量。事實上可以證明這個推論是正確的，稱為高斯散度定理。高斯定理說明，如果在體積V內的向量場A擁有散度，那麼散度的體積分等於向量場在V的表面S的面積分：

$\iiint \limits _{V}\mathrm {div} \mathbf {A} dv=\int \!\!\!\!\int _{S}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\;\;\;\bigcirc \,\,\mathbf {A} \cdot \mathbf {n} dS$

歷史

作為向量分析的基礎概念，散度同樣源自對四元數上的微積分研究。哈密頓在介紹四元數的運算時，將一個四元數$q=A+B{\boldsymbol {i}}+C{\boldsymbol {j}}+D{\boldsymbol {k}}$中的$A$稱為「純量部分」（scalar part），將$B{\boldsymbol {i}}+C{\boldsymbol {j}}+D{\boldsymbol {k}}$稱為「向量部分」（vector part）。他引入了四元數的偏微分算子$\nabla ={\boldsymbol {i}}{\frac {\mathrm {d} }{\mathrm {d} x}}+{\boldsymbol {j}}{\frac {\mathrm {d} }{\mathrm {d} y}}+{\boldsymbol {k}}{\frac {\mathrm {d} }{\mathrm {d} z}}$（即$\nabla$算子）後，計算$\nabla$對一個四元數之向量部分$\sigma =B{\boldsymbol {i}}+C{\boldsymbol {j}}+D{\boldsymbol {k}}$的效果：

$\nabla \sigma =({\boldsymbol {i}}{\frac {\mathrm {d} }{\mathrm {d} x}}+{\boldsymbol {j}}{\frac {\mathrm {d} }{\mathrm {d} y}}+{\boldsymbol {k}}{\frac {\mathrm {d} }{\mathrm {d} z}})(B{\boldsymbol {i}}+C{\boldsymbol {j}}+D{\boldsymbol {k}})$

$=-\left({\frac {\mathrm {d} B}{\mathrm {d} x}}+{\frac {\mathrm {d} C}{\mathrm {d} y}}+{\frac {\mathrm {d} D}{\mathrm {d} z}}\right)+\left(\left({\frac {\mathrm {d} D}{\mathrm {d} y}}-{\frac {\mathrm {d} C}{\mathrm {d} z}}\right){\boldsymbol {i}}+\left({\frac {\mathrm {d} B}{\mathrm {d} z}}-{\frac {\mathrm {d} D}{\mathrm {d} x}}\right){\boldsymbol {j}}+\left({\frac {\mathrm {d} C}{\mathrm {d} x}}-{\frac {\mathrm {d} B}{\mathrm {d} y}}\right){\boldsymbol {k}}\right)$

麥克斯韋在1873年的論文中將其中的「純量部分」：$-\left({\frac {\mathrm {d} B}{\mathrm {d} x}}+{\frac {\mathrm {d} C}{\mathrm {d} y}}+{\frac {\mathrm {d} D}{\mathrm {d} z}}\right)$稱為「聚集度」（Convergence），而將「向量部分」：$\left({\frac {\mathrm {d} D}{\mathrm {d} y}}-{\frac {\mathrm {d} C}{\mathrm {d} z}}\right){\boldsymbol {i}}+\left({\frac {\mathrm {d} B}{\mathrm {d} z}}-{\frac {\mathrm {d} D}{\mathrm {d} x}}\right){\boldsymbol {j}}+\left({\frac {\mathrm {d} C}{\mathrm {d} x}}-{\frac {\mathrm {d} B}{\mathrm {d} y}}\right){\boldsymbol {k}}$稱為「旋度」（Curl）或「變度」（Version）。亥維賽在1883年發表的論文：《電學與磁學中的若干關係》（Some Electrostatic and Magnetic Relations）中討論了靜電場中電場力的聚集度。他計算出在電荷體密度為$\rho$的一點上，有：$4\pi \rho =-\operatorname {conv} \,R={\frac {\mathrm {d} R_{x}}{\mathrm {d} x}}+{\frac {\mathrm {d} R_{y}}{\mathrm {d} y}}+{\frac {\mathrm {d} R_{z}}{\mathrm {d} z}}.\,$其中$R$是電場力。他將這個關係解釋為電荷的存在是電場力匯聚的相反。如果將聚集度解釋為電場力進入一個微小體積的總和，那麼加上一個負號之後，就可以描述一個微小體積中散發出的電場力總和，他將其稱為「散度」（divergence）。他認為有必要將$\nabla$算子對一個四元數$q$的作用效果分開，並將$\nabla q$的向量部分分成散度部分$\operatorname {div} \,q$和旋度部分$\operatorname {curl} \,q$ 。

參閱

• 旋度
• 梯度
• 高斯散度定理