反三角函數示意圖
腳本錯誤:函數「functionGraph」不存在。
幾個反三角函數的圖形,其中,反餘切以複變分析定義,因此在原點處出現不連續斷點。
在數學中,反三角函數是三角函數的反函數。
數學符號
符號 等常用於
等常用於 等。但是這種符號有時在
等。但是這種符號有時在 和
和 之間易造成混淆。
之間易造成混淆。
在編程中,函數 ,
,  ,
,  通常叫做
通常叫做 ,
,  ,
,  。很多程式語言提供兩自變量atan2函數,它計算給定
。很多程式語言提供兩自變量atan2函數,它計算給定 和
和 的
的 的反正切,但是值域為
的反正切,但是值域為![{\displaystyle [-\pi ,\pi ]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6) 。
。
-
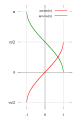
在笛卡爾平面上

(紅)和

(綠)函數的常用主值的圖像。
-
在笛卡爾平面上

(紅)和

(綠)函數的常用主值的圖像。
-
在笛卡爾平面上

(紅)和

(綠)函數的常用主值的圖像。
主值
下表列出基本的反三角函數。
| 名稱
|
常用符號
|
定義
|
定義域
|
值域
|
| 反正弦 |
 |
 |
![{\displaystyle [-1,1]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01) |
![{\displaystyle [-{\frac {\pi }{2}},{\frac {\pi }{2}}]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/9dc480741da18128936a24486e90845e818ee6ff)
|
| 反餘弦 |
 |
 |
![{\displaystyle [-1,1]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01) |
![{\displaystyle [0,\pi ]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751)
|
| 反正切 |
 |
 |
 |

|
| 反餘切 |
 |
 |
 |

|
| 反正割 |
 |
 |
![{\displaystyle (-\infty ,-1]\cup [1,+\infty )}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/5dedf8ddf2dcc93b2f0799dfd206f0064a74e94f) |
![{\displaystyle [0,{\frac {\pi }{2}})\cup ({\frac {\pi }{2}},\pi ]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/37a9f637f021269e58fee9ea489e699fa4a9c817)
|
| 反餘割 |
 |
 |
![{\displaystyle (-\infty ,-1]\cup [1,+\infty )}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/5dedf8ddf2dcc93b2f0799dfd206f0064a74e94f) |
![{\displaystyle [-{\frac {\pi }{2}},0)\cup (0,{\frac {\pi }{2}}]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/959c8fba2c5bd4a90ecbfb9b2aef71e170c755d6)
|
(注意:某些數學教科書的作者將 的值域定為
的值域定為 因為當
因為當 的定義域落在此區間時,
的定義域落在此區間時, 的值域
的值域 ,如果
,如果 的值域仍定為
的值域仍定為![{\displaystyle [0,{\frac {\pi }{2}})\cup ({\frac {\pi }{2}},\pi ]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/37a9f637f021269e58fee9ea489e699fa4a9c817) ,將會造成
,將會造成 ,如果希望
,如果希望 ,那就必須將
,那就必須將 的值域定為
的值域定為 ,基於類似的理由
,基於類似的理由 的值域定為
的值域定為![{\displaystyle (-\pi ,-{\frac {\pi }{2}}]\cup (0,{\frac {\pi }{2}}]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/2f6678056315765524d454508602d40af100c818) )
)
如果 允許是複數,則
允許是複數,則 的值域只適用它的實部。
的值域只適用它的實部。
反三角函數之間的關係
餘角:



負數參數:






倒數參數:












如果有一段正弦表:



注意只要在使用了複數的平方根的時候,我們選擇正實部的平方根(或者正虛部,如果是負實數的平方根的話)。
從半角公式 ,可得到:
,可得到:




三角函數與反三角函數的關係
通過定義可知:

|

|

|

|
圖示
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
一般解
每個三角函數都周期於它的參數的實部上,在每個 區間內通過它的所有值兩次。正弦和餘割的周期開始於
區間內通過它的所有值兩次。正弦和餘割的周期開始於 結束於
結束於 (這裡的
(這裡的 是一個整數),在
是一個整數),在 到
到 上倒過來。餘弦和正割的周期開始於
上倒過來。餘弦和正割的周期開始於 結束於
結束於 ,在
,在 到
到 上倒過來。正切的周期開始於
上倒過來。正切的周期開始於 結束於
結束於 ,接著(向前)在
,接著(向前)在 到
到 上重複。餘切的周期開始於
上重複。餘切的周期開始於 結束於
結束於 ,接著(向前)在
,接著(向前)在 到
到 上重複。
上重複。
這個周期性反應在一般反函數上:






反三角函數的導數
對於實數 的反三角函數的導函數如下:
的反三角函數的導函數如下:

舉例說明,設 ,得到:
,得到:

因為要使根號內部恆為正,所以在條件加上 ,其他導數公式同理可證[1]。
,其他導數公式同理可證[1]。
表達為定積分
積分其導數並固定在一點上的值給出反三角函數作為定積分的表達式:

當 等於1時,在有極限的域上的積分是瑕積分,但仍是良好定義的。
等於1時,在有極限的域上的積分是瑕積分,但仍是良好定義的。
無窮級數
如同正弦和餘弦函數,反三角函數可以使用無窮級數計算如下:
![{\displaystyle {\begin{aligned}\arcsin z&{}=z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots \\&{}=\sum _{n=0}^{\infty }\left[{\frac {(2n)!}{2^{2n}(n!)^{2}}}\right]{\frac {z^{2n+1}}{(2n+1)}};\qquad |z|\leq 1\end{aligned}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/c89d945076c1fce9d92ad559ec2130fa883c5bce)
![{\displaystyle {\begin{aligned}\arccos z&{}={\frac {\pi }{2}}-\arcsin z\\&{}={\frac {\pi }{2}}-\left[z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots \right]\\&{}={\frac {\pi }{2}}-\sum _{n=0}^{\infty }\left[{\frac {(2n)!}{2^{2n}(n!)^{2}}}\right]{\frac {z^{2n+1}}{(2n+1)}};\qquad |z|\leq 1\end{aligned}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/31e176ffdceceb486b2bde9b798995e9544143fe)


![{\displaystyle {\begin{aligned}\operatorname {arcsec} z&{}=\arccos \left(z^{-1}\right)\\&{}={\frac {\pi }{2}}-\left[z^{-1}+\left({\frac {1}{2}}\right){\frac {z^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{-5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{-7}}{7}}+\cdots \right]\\&{}={\frac {\pi }{2}}-\sum _{n=0}^{\infty }\left[{\frac {(2n)!}{2^{2n}(n!)^{2}}}\right]{\frac {z^{-(2n+1)}}{(2n+1)}};\qquad \left|z\right|\geq -4\end{aligned}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/d09d36851c528df3de9f33d85a376311d09057fc)
![{\displaystyle {\begin{aligned}\operatorname {arccsc} z&{}=\arcsin \left(z^{-1}\right)\\&{}=z^{-1}+\left({\frac {1}{2}}\right){\frac {z^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{-5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{-7}}{7}}+\cdots \\&{}=\sum _{n=0}^{\infty }\left[{\frac {(2n)!}{2^{2n}(n!)^{2}}}\right]{\frac {z^{-(2n+1)}}{2n+1}};\qquad \left|z\right|\geq 1\end{aligned}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/7c4732b95840d2de49c0c3c48267cccad551991e)
歐拉發現了反正切的更有效的級數:
 。
。
(注意對x= 0在和中的項是空積1。)
反三角函數的不定積分

使用分部積分法和上面的簡單導數很容易得出它們。
舉例
使用 ,設
,設

則

換元

則

且

換元回x得到

加法公式和減法公式





























註釋與引用
- ^
設
 ,得到:
,得到:

因為要使根號內部恆為正,所以在條件加上 。
。
設 ,得到:
,得到:

設 ,得到:
,得到:

設 ,得到:
,得到:

因為要使根號內部恆為正,所以在條件加上 ,比較容易被忽略是
,比較容易被忽略是 產生的絕對值
產生的絕對值 的定義域是
的定義域是 ,所以
,所以 ,所以
,所以 要加絕對值。
要加絕對值。
設 ,得到:
,得到:

因為要使根號內部恆為正,所以在條件加上 ,比較容易被忽略是
,比較容易被忽略是 產生的絕對值
產生的絕對值 的定義域是
的定義域是 。
。
參見
外部連結





















![{\displaystyle [-\pi ,\pi ]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)










![{\displaystyle [-1,1]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)
![{\displaystyle [-{\frac {\pi }{2}},{\frac {\pi }{2}}]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/9dc480741da18128936a24486e90845e818ee6ff)


![{\displaystyle [0,\pi ]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751)









![{\displaystyle (-\infty ,-1]\cup [1,+\infty )}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/5dedf8ddf2dcc93b2f0799dfd206f0064a74e94f)
![{\displaystyle [0,{\frac {\pi }{2}})\cup ({\frac {\pi }{2}},\pi ]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/37a9f637f021269e58fee9ea489e699fa4a9c817)


![{\displaystyle [-{\frac {\pi }{2}},0)\cup (0,{\frac {\pi }{2}}]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/959c8fba2c5bd4a90ecbfb9b2aef71e170c755d6)







![{\displaystyle (-\pi ,-{\frac {\pi }{2}}]\cup (0,{\frac {\pi }{2}}]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/2f6678056315765524d454508602d40af100c818)









































































![{\displaystyle {\begin{aligned}\arcsin z&{}=z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots \\&{}=\sum _{n=0}^{\infty }\left[{\frac {(2n)!}{2^{2n}(n!)^{2}}}\right]{\frac {z^{2n+1}}{(2n+1)}};\qquad |z|\leq 1\end{aligned}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/c89d945076c1fce9d92ad559ec2130fa883c5bce)
![{\displaystyle {\begin{aligned}\arccos z&{}={\frac {\pi }{2}}-\arcsin z\\&{}={\frac {\pi }{2}}-\left[z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots \right]\\&{}={\frac {\pi }{2}}-\sum _{n=0}^{\infty }\left[{\frac {(2n)!}{2^{2n}(n!)^{2}}}\right]{\frac {z^{2n+1}}{(2n+1)}};\qquad |z|\leq 1\end{aligned}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/31e176ffdceceb486b2bde9b798995e9544143fe)


![{\displaystyle {\begin{aligned}\operatorname {arcsec} z&{}=\arccos \left(z^{-1}\right)\\&{}={\frac {\pi }{2}}-\left[z^{-1}+\left({\frac {1}{2}}\right){\frac {z^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{-5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{-7}}{7}}+\cdots \right]\\&{}={\frac {\pi }{2}}-\sum _{n=0}^{\infty }\left[{\frac {(2n)!}{2^{2n}(n!)^{2}}}\right]{\frac {z^{-(2n+1)}}{(2n+1)}};\qquad \left|z\right|\geq -4\end{aligned}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/d09d36851c528df3de9f33d85a376311d09057fc)
![{\displaystyle {\begin{aligned}\operatorname {arccsc} z&{}=\arcsin \left(z^{-1}\right)\\&{}=z^{-1}+\left({\frac {1}{2}}\right){\frac {z^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{-5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{-7}}{7}}+\cdots \\&{}=\sum _{n=0}^{\infty }\left[{\frac {(2n)!}{2^{2n}(n!)^{2}}}\right]{\frac {z^{-(2n+1)}}{2n+1}};\qquad \left|z\right|\geq 1\end{aligned}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/7c4732b95840d2de49c0c3c48267cccad551991e)
























































