二十面體半形
 | |||
| 類別 | 抽象多胞形 射影多面體 | ||
|---|---|---|---|
| 對偶多面體 | 十二面體半形 | ||
| 數學表示法 | |||
| 施萊夫利符號 | {3,5}/2 or {3,5}5 | ||
| 性質 | |||
| 面 | 10 | ||
| 邊 | 15 | ||
| 頂點 | 6 | ||
| 歐拉特徵數 | F=10, E=15, V=6 (χ=1) | ||
| 組成與佈局 | |||
| 頂點圖 | 3.3.3.3.3 | ||
| 對稱性 | |||
| 對稱群 | A5, 60階 | ||
| 特性 | |||
| 不可定向、 歐拉示性數 | |||
| 圖像 | |||
| |||
在抽象幾何學中,二十面體半形是一種抽象正多面體,有著正二十面體一半的面。二十面體半形可被視為是一種影射多面體,可視為由十個三角形構成的實射影平面鑲嵌。
性質
二十面體半形是一種抽象正多面體,共由10個面、15條邊和6個頂點組成;其中所有10個面都是正三角形、每個頂點都是5個正三角形的公共頂點,在施萊夫利符號中可以用{3,5}5[1]或{3,5}/2[2]來表示,其中{3,5}代表且每個頂點都是5個正三角形的公共頂點,然而{3,5}代表正常的正二十面體,因此用{3,5}5符號來表示二十面體半形[3]。二十面體半形的皮特里多邊形為五邊形。[4]
 二十面體半形 |
 二十面體半形的對偶多面體 十二面體半形 |
二十面體半形的對稱群為A5考克斯特群。所有多面體中僅有2種多面體具備A5考克斯特群對稱性[6],另外一個與A5考克斯特群對應的半形體為大十二面體半形。[7]
具象化
二十面體半形是一個抽象多面體,其無法實體存在,但可以透過一些手段來具象化。其中一種方式是使用其對應的正則地區圖來具象化。二十面體半形對應的正則地區圖可被具象為一個五維空間扭歪正多面體,該多面體所有6個頂點和15條邊皆位於五維正六胞體上[8],而原有五維正六胞體有20個三角形面,而對應的二十面體半形之扭歪多面體具象化則僅交錯地取其中10個面[9],並且相鄰的2個面位於相同三維平坦空間中,但整體立體不位於相同三維空間中,因此是一個扭歪多面體。[10]在這個具象化中,其三角形-三角形二面角為3的反正割值(弧度,約70.5287795度),與一般正二十面體的三角形-三角形二面角(弧度,約138.189685度)不同。 [10]
在拓樸學上,二十面體半形與四面半六面體相關。若將四面半六面體的每一個正方形面替換為2個三角形,則所形成的立體若只看面之間的相鄰關係,會與二十面體半形無異,即每個頂點都是5個三角形,且由10個面(4個正三角形與6個直角三角形)、15條邊(12條四面半六面體的邊與3條正方形面替換為2個三角形時形成的邊)和6個頂點組成。[11]
圖像
二十面體半形的邊,頂點可以對稱地表示為一個施萊格爾圖。

|
| 以為面中心 |
|---|
完全圖K6
二十面體半形和五維正六胞體有著相同的邊以及頂點,但只有其一半數量的面[9]。而五維正六胞體對應的骨架圖為完全圖,即有著六個頂點的完全圖[9],因此圖論的角度來看,二十面體半形可以視為是嵌入於實射影平面完全圖。其對應的對偶圖皮特森圖也對應到了二十面體半形的對偶多面體十二面體半形。[12]

相關多面體
相關半形體
正二十面體可以經過一系列的多面體變換轉變為半正多面體,部分半正多面體也存在對應的半形體,例如截角二十面體半形、截半二十面體半形等[13][14]。
截角二十面體半形
截角二十面體半形是截角二十面體的半形體,又稱為足球半形(Hemi-Soccer Ball)。其出現在四維正五十七胞體的一種具象化的第二層結構中[15],由16個面、45條邊和30個頂點組成。其可透過將截角二十面體的每個頂點與對應的對蹠點合併構成[13][16]。
截半二十面體半形
截半二十面體半形是截半二十面體的半形體。其也可以透過將二十面體半形或十二面體半形進行截半變換構成。[14]
相關皮特里對偶
部分皮特里對偶與正二十面體或其半形體相關,例如二十面體半形的皮特里對偶或正二十面體的皮特里對偶。[17]
二十面體半形的皮特里對偶
二十面體半形的皮特里多邊形為五邊形[4],其對應的皮特里對偶為每個頂點由5個五邊形(二十面體半形的皮特里多邊形)組成的抽象多面體。這個抽象多面體是一個自身對偶多面體,並且可以被小星形十二面體、大十二面體或其他等價於虧格為5的{5,5}幾何結構(的表面)二重覆蓋[17][18]。這個幾何體對應的骨架圖與二十面體半形相同,皆為K6完全圖。[17]
皮特里二十面體
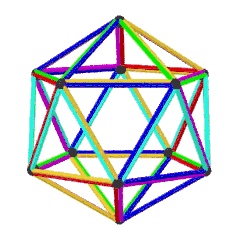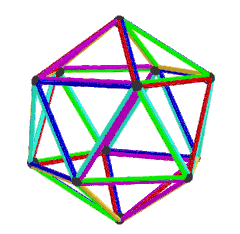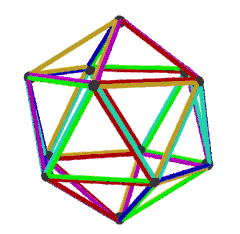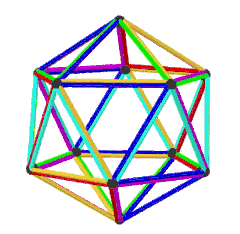 (以不同顏色表示每個面) | |
| 類別 | 皮特里對偶 正則地區圖 |
|---|---|
| 數學表示法 | |
| 施萊夫利符號 | {3,5}π |
| 性質 | |
| 面 | 6 |
| 邊 | 30 |
| 頂點 | 12 |
| 歐拉特徵數 | F=6, E=30, V=12 (χ=-12) |
| 二面角 | (不存在) |
| 對稱性 | |
| 對稱群 | Ih, H3, [5,3], *532 |
| 特性 | |
| 扭歪、正則 | |
皮特里二十面體是正二十面體的皮特里對偶,可以透過將原有正二十面體上取皮特里多邊形構成,換句話說,皮特里二十面體為由正二十面體的皮特里多邊形構成的立體[19]。由於正二十面體的皮特里多邊形為扭歪十邊形,因此無法確立其封閉範圍,故無法計算其表面積和體積。
皮特里二十面體是一個不可定向且虧格為14的幾何結構[20]。皮特里二十面體共有6個面、30條邊和12個頂點。其中面由6個扭歪十邊形面組成,每個頂點都是5個扭歪十邊形的公共頂點。[20]
 二十面體的皮特里多邊形 |
 構成皮皮特里二十面體的扭歪十邊形面 |
皮特里二十面體與正二十面體互為皮特里對偶,也就是說,皮特里二十面體的皮特里對偶為正二十面體,換句話說,即皮特里二十面體的皮特里多邊形為三角形[20][21]。
皮特里大十二面體與皮特里小星形十二面體
  左:皮特里大十二面體 右:皮特里小星形十二面體 | |
| 類別 | 皮特里對偶 正則地區圖 |
|---|---|
| 數學表示法 | |
| 施萊夫利符號 | 皮特里大十二面體:{5,5/2}π 皮特里小星形十二面體:{5/2,5}π |
| 性質 | |
| 面 | 10 |
| 邊 | 30 |
| 頂點 | 12 |
| 歐拉特徵數 | F=10, E=30, V=12 (χ=-8) |
| 二面角 | (不存在) |
| 對稱性 | |
| 對稱群 | Ih, H3, [5,3], *532 |
| 特性 | |
| 扭歪、正則 | |
皮特里大十二面體是大十二面體的皮特里對偶,由大十二面體的皮特里多邊形組成。由於大十二面體與小星形十二面體對應相同的正則地區圖[22],因此皮特里大十二面體對應的正則地區圖也與皮特里小星形十二面體相同,皆由10個面、30條邊和12個頂點組成[23]。
 構成皮特里大十二面體的扭歪六邊形面 |
 構成皮特里小星形十二面體的扭歪六邊形面 |
其對應的骨架為正二十面體。[22]
| 名稱 | 構成面 |
|---|---|
 皮特里二十面體 |
 扭歪十邊形 |
 皮特里大十二面體 |
 扭歪六邊形 |
參見
參考文獻
- ^ Ellers, Erich W. Erich W. Ellers, Branko Grünbaum, Peter McMullen, Asia Ivic Weiss. NOTICES OF THE AMS. 2003, 50 (10).
- ^ Schulte, Egon. Classification of locally toroidal regular polytopes. Polytopes: Abstract, convex and computational (Springer). 1994: 125––154.
- ^ McMullen, Peter; Schulte, Egon, 6C. Projective Regular Polytopes, Abstract Regular Polytopes 1st, Cambridge University Press: 162–165, December 2002, ISBN 0-521-81496-0
- ^ 4.0 4.1 Monson, Barry and Ivić Weiss, Asia. Cayley graphs and symmetric 4-polytopes. Ars Mathematica Contemporanea. 2008, 1 (2).
- ^ Hartley, Michael I. The Classification of Rank 4 Locally Projective Polytopes and Their Quotients. arXiv preprint math/0310429. 2003.
- ^ Fernandes, Maria Elisa and Leemans, Dimitri and Mixer, Mark. Polytopes of high rank for the alternating groups. Journal of Combinatorial Theory, Series A (Elsevier). 2012, 119 (1): 42––56.
- ^ Fernandes, Maria Elisa and Leemans, Dimitri and Mixer, Mark. All Alternating Groups with Have Polytopes of Rank . SIAM Journal on Discrete Mathematics (Society for Industrial and Applied Mathematics). 2012, 26 (2): 482. doi:10.1137/110838467.
- ^ Coxeter, Harold Scott Macdonald, Twelve geometric essays, Carbondale: Southern Illinois University Press: 80, 1968
- ^ 9.0 9.1 9.2 Séquin, Carlo H, A 10-Dimensional Jewel, Gathering for Gardner G4GX, Atlanta, GA, 2012
- ^ 10.0 10.1 Coxeter, HSM, A symmetrical arrangement of eleven hemi-icosahedra, North-Holland Mathematics Studies (Elsevier), 1984, 87: pp. 103–114
- ^ Gailiunas, Paul; et al, Polyhedral Models of the Projective Plane, Bridges 2018 Conference Proceedings, 2018: 543–546
- ^ Melikhov, Sergey A. Combinatorics of embeddings. arXiv preprint arXiv:1103.5457. 2011.
- ^ 13.0 13.1 The Hemi-Soccer Ball. wmich.edu.
- ^ 14.0 14.1 The hemi-icosidodecahedron. Regular Map database - map details. [2021-07-30].
- ^ Séquin, Carlo and Hamlin, James. The regular 4-dimensional 57-cell. ACM SIGGRAPH 2007 Sketches, SIGGRAPH'07. 2007-08. doi:10.1145/1278780.1278784.
- ^ Carlo H. Séquin; James F. Hamlin. The Regular 4-Dimensional 11-cell and 57-cell. SIGGRAPH 2007, San Diego, University of California, Berkeley.
- ^ 17.0 17.1 17.2 C5:{5,5}. Regular Map database - map details. [2021-07-30].
- ^ S4:{5,5}. Regular Map database - map details. [2021-07-30].
- ^ Gorini, Catherine A., Geometry at Work, MAA Notes 53, Cambridge University Press: 181, 2000, ISBN 9780883851647
- ^ 20.0 20.1 20.2 N14.3′. Regular Map database - map details. [2021-08-05].
- ^ The icosahedron. Regular Map database - map details. [2021-08-04].
- ^ 22.0 22.1 S4:{5,5}. Regular Map database - map details, weddslist.com. [2021-07-30].
- ^ N10.5′. Regular Map database - map details, weddslist.com. [2021-07-30].









