跳转到内容

擬詹森多面體

本页使用了标题或全文手工转换
维基百科，自由的百科全书

这是本页的一个历史版本，由A2569875（留言 | 贡献）在2023年1月23日 (一) 12:56 （→例子）编辑。这可能和当前版本存在着巨大的差异。

在幾何學中，擬詹森多面體是嚴格凸多面體，其面幾乎都是正多邊形，但其中有部分或全部的面不是正多邊形但很接近正多邊形。這種多面體也包含詹森多面體，即所有的面都是正多邊形，而擬詹森多面體經常會有在物理構造沒有注意到的差異在正多邊形與非正多邊形之間[1]。近似的精確值取決於這樣一個多面體的面逼近正多邊形的程度。

例子

名稱
康威多面體表示法		 Image Vertex
configurations		 V E F F3 F4 F5 F6 F8 F10 F12 對稱性（英语：List of spherical symmetry groups）
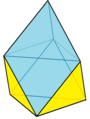
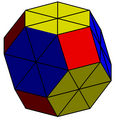
Truncated triangular bipyramid
t4dP3		 2 (5.5.5)
12 (4.5.5)		 14 21 9 3 6 Dih3
order 12
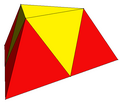
Truncated triakis tetrahedron
t6kT 		4 (5.5.5)
24 (5.5.6) 		28 42 16     12 4       Td, [3,3]
order 24
Pentahexagonal pyritoheptacontatetrahedron 12 (3.5.3.6)
24 (3.3.5.6)
24 (3.3.3.3.5) 		60 132 74 56 12 6 Th, [3+,4]
order 24
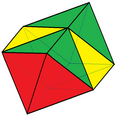
Chamfered cube
cC 		24 (4.6.6)
8 (6.6.6) 		32 48 18   6   12       Oh, [4,3]
order 48
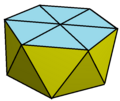
-- 12 (5.5.6)
6 (3.5.3.5)
12 (3.3.5.5) 		30 54 26 12   12 2       D6h, [6,2]
order 24
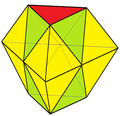
-- 6 (5.5.5)
9 (3.5.3.5)
12 (3.3.5.5) 		27 51 26 14   12         D3h, [3,2]
order 12
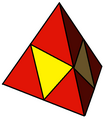
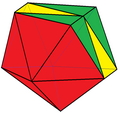
Tetrated dodecahedron 4 (5.5.5)
12 (3.5.3.5)
12 (3.3.5.5) 		28 54 28 16   12         Td, [3,3]
order 24
部分截半截角八面體 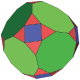24 (3.4.3.9)
24 (3.9.9) 		38 84 48 24 6           Oh, [4,3]
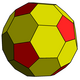
Chamfered dodecahedron
cD 		60 (5.6.6)
20 (6.6.6) 		80 120 42     12 30       Ih, [5,3]
order 120
Rectified truncated icosahedron
atI 		60 (3.5.3.6)
30 (3.6.3.6) 		90 180 92 60   12 20       Ih, [5,3]
order 120
Truncated truncated icosahedron
ttI 		120 (3.10.12)
60 (3.12.12) 		180 270 92 60         12 20 Ih, [5,3]
order 120
Expanded truncated icosahedron
etI 		60 (3.4.5.4)
120 (3.4.6.4) 		180 360 182 60 90 12 20       Ih, [5,3]
order 120
Snub rectified truncated icosahedron
stI 		60 (3.3.3.3.5)
120 (3.3.3.3.6) 		180 450 272 240   12 20       I, [5,3]+
order 60


名稱 圖像 頂點圖 V E F F3 F4 F5 F6 F8 F9 F10 對稱群
截角三角化四面體 4 (5.5.5)
24 (5.5.6) 		28 42 16     12 4       Td
-- 6 (5.5.5)
9 (3.5.3.5)
12 (3.3.5.5) 		27 51 26 14   12         D3h
四階十二面體 4 (5.5.5)
12 (3.5.3.5)
12 (3.3.5.5) 		28 54 28 16   12         Td
-- 12 (5.5.6)
6 (3.5.3.5)
12 (3.3.5.5) 		30 54 26 12   12 2       D6h

共面擬詹森多面體

有些未能成為詹森多面體的候選多面體是因為其存在有兩個以上共面的面。這些多面體可被看做是凸的面切非常接近正多邊形。

例如： 3.3...

4.4.4.4

3.4.6.4:

  • 正六角帳塔 (退化)
    正六角帳塔
    (退化)

參見

參考文獻

  1. ^ Kaplan, Craig S.; Hart, George W., Symmetrohedra: Polyhedra from Symmetric Placement of Regular Polygons, Bridges: Mathematical Connections in Art, Music and Science (PDF), 2001 [2014-05-01], （原始内容存档 (PDF)于2015-09-23） .
检索自“https://zh.wikipedia.org/zhwiki/w/index.php?title=擬詹森多面體&oldid=75652964”