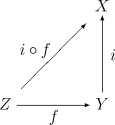在拓扑学和数学的其他相关领域里,拓扑空间  的子空间是指在
的子空间是指在  中子集
中子集  及在
及在  上赋予的由
上赋予的由  的拓扑所导出的拓扑。这个导出的拓扑叫做
的拓扑所导出的拓扑。这个导出的拓扑叫做  的拓扑在
的拓扑在  上的子空间拓扑,也称为相对拓扑。导出方式参见 #定义。
上的子空间拓扑,也称为相对拓扑。导出方式参见 #定义。
给定拓扑空间  和
和  内的子集
内的子集  ,于
,于  上的子空间拓扑被定义为
上的子空间拓扑被定义为

亦即, 的子集于子空间拓扑中为开集当且仅当其为
的子集于子空间拓扑中为开集当且仅当其为  和一于
和一于  内的开集的交集。若
内的开集的交集。若  被设上子空间拓扑,则其本身即为一拓扑空间,并被称之为
被设上子空间拓扑,则其本身即为一拓扑空间,并被称之为  的子空间。除非有额外叙述,一般拓扑空间的子集都会假定设有一子空间拓扑。
的子空间。除非有额外叙述,一般拓扑空间的子集都会假定设有一子空间拓扑。
若  为
为  内的开集、闭集或稠密集,则分别称
内的开集、闭集或稠密集,则分别称  为
为  内的一开子空间、闭子空间或稠密子空间。
内的一开子空间、闭子空间或稠密子空间。
另外,也可以定义  内的子集
内的子集  的子空间拓扑为会使得内含映射
的子空间拓扑为会使得内含映射

为连续的最弱拓扑。
更一般地,设  为一由集合
为一由集合  至拓扑空间
至拓扑空间  的单射,则于
的单射,则于  上的子空间拓扑即为定义为
上的子空间拓扑即为定义为  为连续的最弱拓扑。此拓扑的开集恰好会是
为连续的最弱拓扑。此拓扑的开集恰好会是  的其中一个,其中的
的其中一个,其中的  为
为  内的开集。
内的开集。 因此同胚于在
因此同胚于在  内的值域(也是带子空间拓扑),且
内的值域(也是带子空间拓扑),且  会被称之为拓扑嵌入。
会被称之为拓扑嵌入。
如果单射  是一个开映射,那么子空间
是一个开映射,那么子空间  被称为一个开子空间;同样地,如果单射
被称为一个开子空间;同样地,如果单射  是一个闭映射,那么子空间
是一个闭映射,那么子空间  被称为一个闭子空间。
被称为一个闭子空间。
子空间拓朴具有以下特性。设  是
是  的一个子空间且
的一个子空间且  是一个内含映射。对于任何拓朴空间
是一个内含映射。对于任何拓朴空间  ,
, 是连续映射当且仅当合成映射
是连续映射当且仅当合成映射  是连续的。
是连续的。
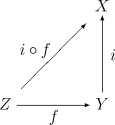
这个特性可以被用来定义  上的子空间拓朴。我们列出一些更进一步的性质。设
上的子空间拓朴。我们列出一些更进一步的性质。设  是
是  的子空间拓朴。
的子空间拓朴。
- 如果
 是连续的,那么
是连续的,那么  到
到  的限制也是连续的。
的限制也是连续的。
- 如果
 是连续的,那么
是连续的,那么  也是连续的。
也是连续的。
 中的闭集是,严谨地来说,
中的闭集是,严谨地来说, 与
与  中闭集的交集。
中闭集的交集。- 如果
 是
是  的一个子空间,那么
的一个子空间,那么  也是
也是  的一个子空间。换言之,
的一个子空间。换言之, 从
从  继承的子空间拓朴与从
继承的子空间拓朴与从  继承的一样。
继承的一样。
- 假设
 是
是  的一个开子空间(则
的一个开子空间(则  ),那么
),那么  的子集合在
的子集合在  中是开的当且仅当其在
中是开的当且仅当其在  中是开的。
中是开的。
- 假设
 是
是  的一个闭子空间(则
的一个闭子空间(则  ),那么
),那么  的子集合在
的子集合在  中是闭的当且仅当其在
中是闭的当且仅当其在  中是闭的。
中是闭的。
- 如果
 是
是  的基,那么
的基,那么  是
是  的基。
的基。
- 透过限制度量到一个子集,度量空间上的导出拓朴会导出对于这个子集的子空间拓朴。
如果一个拓朴空间的一些拓朴不变量能够保证它们的子空间也有相同的性质,那么我们称这些性质具有可遗传性。如果某些性质只有保证闭子空间才拥有,那我们称这些性质具有弱遗传性。
- Bourbaki, Nicolas, Elements of Mathematics: General Topology, Addison-Wesley (1966)
- Steen, Lynn A. and Seeback, J. Arthur Jr., Counterexamples in Topology, Holt, Rinehart and Winston (1970) ISBN 0-03-079485-4.
- Wilard, Stephen. General Topology, Dover Publications (2004) ISBN 0-486-43479-6