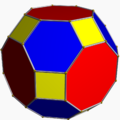
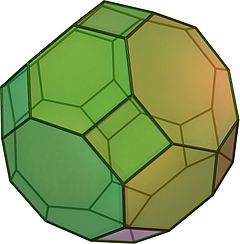
大斜方截半立方体
 (按這裡觀看旋轉模型) | |||||
| 類別 | 半正多面體 | ||||
|---|---|---|---|---|---|
| 對偶多面體 | 四角化菱形十二面體 | ||||
| 識別 | |||||
| 名稱 | 大斜方截半立方体 | ||||
| 參考索引 | U11, C23, W15 | ||||
| 鮑爾斯縮寫 | girco | ||||
| 數學表示法 | |||||
| 考克斯特符號 | |||||
| 施萊夫利符號 | tr{4,3} | ||||
| 威佐夫符號 | 2 3 4 | | ||||
| 康威表示法 | bC taC | ||||
| 性質 | |||||
| 面 | 26 | ||||
| 邊 | 72 | ||||
| 頂點 | 48 | ||||
| 歐拉特徵數 | F=26, E=72, V=48 (χ=2) | ||||
| 組成與佈局 | |||||
| 面的種類 | 正方形 正六邊形 正八邊形 | ||||
| 面的佈局 | 12個{4} 8個{6} 6個{8} | ||||
| 頂點圖 | 4.6.8 | ||||
| 對稱性 | |||||
| 對稱群 | Oh群 | ||||
| 特性 | |||||
| 環帶多面體 | |||||
| 圖像 | |||||
| |||||
在幾何學中,大斜方截半立方體,又稱為截角截半立方體,是一種阿基米德立體。這個多面體共由26個面、72條邊和48個頂點所組成,其中,26個面中包含了 12個正方形面、8個正六邊形面以及6個正八邊形面。由於每個面都存在點對稱性質,因此大斜方截半立方體也是一種環帶多面體。
其他名稱
這個立體有多種名稱:
- 大斜方截半立方體(英語:Great rhombicuboctahedron[註 1]),由Robert Williams命名[1]
- 截角截半立方體(英語:Truncated Cuboctahedron),由約翰尼斯·克卜勒命名[2]
- 斜方截角立方體(英語:Rhombitruncated cuboctahedron),由Magnus Wenninger命名[3]
- 大斜方截半立方體(英語:Great rhombcuboctahedron[註 1]),由Peter Cromwell命名[4]
- 全截立方體(英語:Omnitruncated cube or cantitruncated cube),由諾曼·約翰遜命名
名稱截角截半立方體(英語:Truncated Cuboctahedron)最初是約翰尼斯·克卜勒命的名稱,但這個名稱有點會引起誤解,因為若將截半立方體進行截角操作的話,即切去截半立方體的所有頂點之後,得到的立體圖形將不會是均勻的形狀,會出現長方形的面,但由於他們可以藉由變形變成半正多面體大斜方截半立方體,因此他們在拓樸學上是一樣的[5]。
性質
大斜方截半立方體是一種阿基米德立體,由於每一個面都是正多邊形,因此也符合托羅爾德戈塞特在1900為給出的半正多面體定義[6][7]。此外,大斜方截半立方體也是一種環帶多面體,並屬於八面體對稱。
面的組成
大斜方截半立方體是一種半正多面體,換言之即其面皆由正多邊形組成。大斜方截半立方體具有26個面,因此也可以稱為半正二十六面體,但半正二十六面體不只一種,小斜方截半立方体也是一個具有26個面的半正多面體。組成大斜方截半立方體的26個面中,其中12個面是正方形面、8個面是正六邊形面以及另外6個正八邊形的面。
頂點座標
若有一個邊長為2的大斜方截半立方體之幾何中心置於三維直角坐標系的原點時,其頂點座標為下列座標的全排列:
體積與表面積
其中A代表表面積約為62倍的邊長平方、V代表體積約為42倍的邊長立方。
作法
構成大斜方截半立方體有多種方法,其中一種是將立方體(或正八面體)的十二條棱切一刀,並且在八個(正八面體為六個)頂點處切一刀,但是要切的薄一點,切的深度與截半相當,就可以得到一個大斜方截半立方體。
拆解
| 虧格 3 | 虧格 5 | 虧格 7 | 虧格 11 |
|---|---|---|---|

|

|

|

|
正交投影
| 建立於 | 頂點 | 四邊形-六邊形 交棱 |
四邊形-八邊形 交棱 |
四邊形-八邊形 交棱 |
四邊形-六邊形 交面 |
|---|---|---|---|---|---|
| 圖像 | 
|

|

|

|

|
| 投影對稱性 | [2]+ | [2] | [2] | [2] | [2] |
| 建立於 | 正方形面 | 正八邊形面 | 正方形面 | 正六邊形面 | 正八邊形面 |
| 圖像 | 
|

|

|

|

|
| 投影對稱性 | [2] | [2] | [2] | [6] | [8] |
相關多面體及鑲嵌
| 半正八面體群多面體 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 對稱性: [4,3], (*432) | [4,3]+ (432) |
[1+,4,3] = [3,3] (*332) |
[3+,4] (3*2) | |||||||
| {4,3} | t{4,3} | r{4,3} r{31,1} |
t{3,4} t{31,1} |
{3,4} {31,1} |
rr{4,3} s2{3,4} |
tr{4,3} | sr{4,3} | h{4,3} {3,3} |
h2{4,3} t{3,3} |
s{3,4} s{31,1} |
= |
= |
= |
||||||||
| 半正對偶多面體 | ||||||||||
| V43 | V3.82 | V(3.4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |
大斜方截半立方體圖
| 大斜方截半立方體圖 | |
|---|---|
 4重對稱性 | |
| 顶点 | 48 |
| 边 | 72 |
| 自同构群 | 48 |
| 色数 | 2 |
| 属性 | 立方體, 哈密頓, 正, 零對稱性 |
在圖論的數學領域中,大斜方截半立方體圖是阿基米得立體中大斜方截半立方體之邊與頂點的圖。共有48個頂點和72條稜,且是位於零對稱性和立方體的阿基米德圖[8]。
參見
註釋
參考文獻
- ^ Williams, Robert. The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. 1979. ISBN 0-486-23729-X. (Section 3-9, p. 82)
- ^ Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 138, 1987.
- ^ Wenninger, Magnus, Polyhedron Models, Cambridge University Press, 1974, ISBN 978-0-521-09859-5, MR 0467493 (Model 15, p. 29)
- ^ Cromwell, P.; Polyhedra, CUP hbk (1997), pbk. (1999). (p. 82)
- ^ Cundy, H. and Rollett, A. "Great Rhombicuboctahedron or Truncated Cuboctahedron. 4.6 .8." §3.7.6 in Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., p. 106, 1989.
- ^ Thorold Gosset On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- ^ Coxeter, H.S.M. Regular polytopes, 3rd Edn, Dover (1973)
- ^ Read, R. C.; Wilson, R. J., An Atlas of Graphs, Oxford University Press: 269, 1998
- Cromwell, P. Polyhedra. United Kingdom: Cambridge. 1997: 79–86 Archimedean solids. ISBN 0-521-55432-2.
外部連結
- 埃里克·韦斯坦因. Great rhombicuboctahedron. MathWorld.
- Klitzing, Richard. 3D convex uniform polyhedra x3x4x - girco. bendwavy.org.
- Editable printable net of a truncated cuboctahedron with interactive 3D view
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- great Rhombicuboctahedron: paper strips for plaiting