维基百科:知识问答/存档/2024年5月

本页是以往讨论的存档。请勿编辑本页。若您想发起新讨论或重启现有讨论，请在当前讨论页进行。

伪基百科诽谤文章

https://zh.uncyclopedia.info/wiki/%E4%B8%80%E8%A6%BD%E4%B8%AD%E6%96%87%E7%B6%AD%E5%9F%BA%E4%BA%BA 这篇条目根本就不是讽刺，而且直接骂人的。据我所知有一两个我认识的用户被他们骂了，这样的垃圾文章该怎么办--Hzt0208042508415531 tw（留言） 2024年4月24日 (三) 11:17 (UTC)

伪基的事不归我们社群管，爱怎样就怎样。或者建议基金会去管？

——Sakamotosan路过围观 | 避免做作，免敬 2024年4月30日 (二) 08:54 (UTC)

我也上榜了，原因是因为我在新疆棉花事件引用了一个Twitter一手来源做给一个标注{{需要来源}}的描述脚注？不过比起其他人来说，好像问题一般般。因为按照脚注对应的描述，交流者自述是经济学人（当时的）中国事务编辑，身份正经，看上去有问题吗？（虽然按照本站的来源规则，最好应该是参注新闻媒体对这个交流的引述报道）至于引述Twitter一手来源的，对不住，声优或者ACG类的还真是经常这样引注。

二哈——Sakamotosan路过围观 | 避免做作，免敬 2024年4月30日 (二) 08:54 (UTC)

翻一下历史，居然这句话是我加的，我是从哪里找到这句话的？

囧rz……——Sakamotosan路过围观 | 避免做作，免敬 2024年4月30日 (二) 09:01 (UTC)

管理员Ericliu1912有伪基百科账户，和伪基百科人员关系还不错(?)也许找他讨论看看？请他和那边的管理员沟通？--

{\ce {Be + He->B+ +e- +H- +e+}}

，这是β衰变和正电子发射，请无视其他能量释放。 2024年5月1日 (三) 01:40 (UTC)

我试过了，没有用。实际上伪基百科方面的若干管理人员与维基百科都有过节，对处理此类条目往往意兴阑珊；你看连影武者都能大摇大摆在那边活跃诽谤维基百科及维基人就知道了。甚至对于侵犯个人隐私的资讯，他们也不愿意删除，可以说是非常糟糕。—— Eric Liu_{創造は生命（留言・留名・学生会）} 2024年5月1日 (三) 02:47 (UTC)

关于中国中央电视台新闻频道以ai创作的流感防疫广告中出现了迪士尼皮克斯制作的《寻梦环游记》中角色的元素，这是否构成对迪士尼的侵权？迪士尼公司是否需要寻求法律维权？

如题。 -■■■■（留言） 2024年4月30日 (二) 06:10 (UTC)

哪则广告。--YF dyh000（留言） 2024年4月30日 (二) 14:32 (UTC)

https://www.bilibili.com/video/BV1cm411f7vp/ --■■■■（留言） 2024年5月1日 (三) 00:48 (UTC)

网页是不是打不开？你去B站直接搜BV1cm411f7vp--■■■■（留言） 2024年5月2日 (四) 14:02 (UTC)

我看过了，我觉得很像。目前说不出更多值得参考的观点。--YF dyh000（留言） 2024年5月2日 (四) 14:10 (UTC)

其实不是迪士尼公司是否需要如何的问题，是敢不敢的问题。--Stanleykswong（留言） 2024年5月3日 (五) 07:51 (UTC)

就算真的侵权，你我路人甲乙能代替人家公司提告吗？

在这臆测半天，直接询问该公司法务部门，是不是能得到比较迅速且正确的解答？

人家公司真的觉得自己权益受损，自然会有动作；反之，我们在这边讨论半天人家也不会动不是？

https://privacy.thewaltdisneycompany.com/en/support/

华特迪士尼公司(The Walt Disney Company)

如有关于华特迪士尼公司(The Walt Disney Company)隐私权政策或隐私权措施的相关问题，请联络：

电子邮件： privacycontact@TWDC.com

电话：(877) 466-6669

地址：华特迪士尼公司(The Walt Disney Company)

500 South Buena Vista Street

Mail Code 7830

Burbank, CA 91521-7667

Hulu

电子邮件：DTC.Hulu-Privacy@disney.com

电话：(855) 738-6978

地址：收件人：法务部

2500 Broadway, 2nd Floor

Santa Monica, CA 90404--Innova（留言） 2024年5月3日 (五) 08:59 (UTC)

中世纪欧洲的官员呈给国王或女王的公事报告称为什么？

如题，其实就是想问中世纪西方类似奏折的东西，该怎么称呼。-KRF（留言） 2024年4月30日 (二) 15:04 (UTC)

欧洲的君主（国王或女王）跟官员之间的关系有点儿像三代时期的中国（尤其是商及春秋），他们之间的 power distance 不大，所以没有正式的奏折，大部分上下沟通都是口述。正式公文称为 Letters，但是很少用，Letters 可以是官员君主（甚至是平民）给君主，亦可以是君主下达的。--Stanleykswong（留言） 2024年5月3日 (五) 07:38 (UTC)

另外，其实中国古代也没有奏折。奏折是清朝中后期（大概相当于欧洲的 Early Modern 时期）才有正式的公文；清初，明朝（大概相当于中世纪后期）用的是本、题本、奏本。再之前也是以口头报告／沟通为主。--Stanleykswong（留言） 2024年5月3日 (五) 07:49 (UTC)

了解了，谢谢。-KRF（留言） 2024年5月3日 (五) 10:28 (UTC)

一元二次方程式判别式为0的重根问题

一元二次方程式 $ax^{2}+bx+c=0$ ，其中 $a,c$ 皆为正数， $b$ 为实数，且 $b^{2}-4ac=0$ ，则

$b^{2}=4ac\to b=\pm {\sqrt {4ac}}=\pm 2{\sqrt {ac}}$ ，

代回原方程式，得

ax^{2}\pm (2{\sqrt {ac}})x+c=0

({\sqrt {a}})^{2}x^{2}\pm (2{\sqrt {a}}{\sqrt {c}})x+({\sqrt {c}})^{2}=0

({\sqrt {a}}x\pm {\sqrt {c}})^{2}=0

{\sqrt {a}}x\pm {\sqrt {c}}=0

{\sqrt {a}}x=\pm {\sqrt {c}}

x=\pm {\frac {\sqrt {c}}{\sqrt {a}}}=\pm {\sqrt {\frac {c}{a}}}

可是判别式 $b^{2}-4ac=0$ 应该就造成重根了，为什么上述计算过程还能推导出2个相异根呢？---游蛇脱壳/克劳棣 2024年5月3日 (五) 11:44 (UTC)

阁下分别考虑了两种b的取值（两个二次函数以y轴呈轴对称），当然有2个相异根（实际上是4个根，两组2个相同的实根）。--自由雨日（留言） 2024年5月3日 (五) 12:18 (UTC)

举例：a=c=1，b=±2，代入一下看看吧。--自由雨日（留言） 2024年5月3日 (五) 12:23 (UTC)

本质是一个逻辑问题，阁下首先并没有说明a，b，c是确定的常数，连这个方程本身都没确定下来，怎么可能确定根的个数呢？（如果阁下第一句的意思是a，b，c就是常数，那么再去将常数b当作未知数去求解=±某个数就更是大错特错的。）--自由雨日（留言） 2024年5月3日 (五) 12:26 (UTC)

阁下应该知道一元二次方程式

ax^{2}+bx+c=0

有公式解

x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}

？不用确定

a,b,c

的个别值，只要知道判别式

b^{2}-4ac

的值，就可以知道（实）根的个数了。

- - 当 $b^{2}-4ac>0$ ，方程式有两实根
  - 当 $b^{2}-4ac=0$ ，方程式有一实根（重根） $x={\frac {-b}{2a}}$
  - 当 $b^{2}-4ac<0$ ，方程式有两虚根

我只是将

x={\frac {-b}{2a}}

以另一个形式表示而已，可是它却有两个值

x=\pm {\sqrt {\frac {c}{a}}}

，这就是问题所在。-游蛇脱壳/克劳棣 2024年5月3日 (五) 13:09 (UTC)

阁下的言论已经和百度贴吧民科吧内容非常相似了，建议再好好思考思考。--自由雨日（留言） 2024年5月3日 (五) 13:18 (UTC)

三角形的内切圆半径、外接圆半径、边长、充分必要条件

某三角形的三边长为a,b,c，其内切圆半径为r，外接圆半径为R

请问“r = (a+b-c)/2”是“R = c/2”的充分必要条件吗？为什么？---游蛇脱壳/克劳棣 2024年5月3日 (五) 11:15 (UTC)

是．证明：必要性：根据R=abc/4S（外接圆公式），代入已知“R=c/2”得，ab=2S；又2S=ab sinC（正弦定理），得C=π/2．于是r=2S/(a+b+c)（内切圆公式）=2S/(a+b+√(a^2+b^2))=(a+b-c)/2．充分性：根据r=2S/(a+b+c)（内切圆公式），代入已知“r=(a+b-c)/2”得：4S=a^2+b^2+2ab-c^2；又a^2+b^2-c^2=2ab cosC（余弦定理），代入得2S=ab(1+cosC)；又2S=ab sinC（正弦定理），得1+cosC=sinC，解得C=kπ/2(k∈Z）；由于C∈(0,π)（三角形内角），故C=π/2，故ab=2S，故R=abc/4S（外接圆公式）=c/2．∎--自由雨日（留言） 2024年5月3日 (五) 12:58 (UTC)

个人建议不要在这里提中学程度的问题。（另外，我中学时候也经常犯各种错误，不保证我的推导一定是准确无误的。）--自由雨日（留言） 2024年5月3日 (五) 13:06 (UTC)

在必要性方面，请问

{\frac {2S}{a+b+{\sqrt {a^{2}+b^{2}}}}}

是如何推导到等于

{\frac {a+b-c}{2}}

呢？

附带一提，比较复杂的数学式，还是建议照H:MATH所教导的书写式子，不然读者实在读得很辛苦。-游蛇脱壳/克劳棣 2024年5月3日 (五) 13:53 (UTC)

分子分母同乘(a+b-√(a^2+b^2))，再代入“ab=2S”。我对简单的问题（“简单”是针对问题性质而言的，主要就是指“中学程度”，不代表我一定会或对）一般不用LaTeX格式。--自由雨日（留言） 2024年5月3日 (五) 14:50 (UTC)

那在下再请教2个简单问题，想知道阁下的做法。谢谢！

第一题

等腰三角形，其内切圆半径与外接圆半径长度之和等于腰长，证明其为等腰直角三角形。

第二题

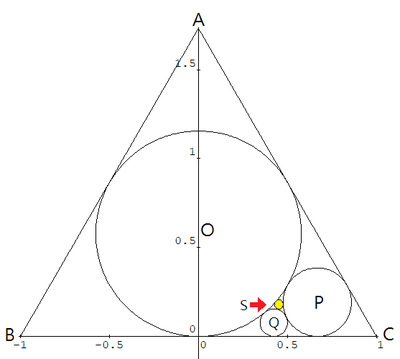
如图，正三角形ABC边长是2，圆O是其内切圆；

圆P与圆O外切，且与AC边、BC边相切；

圆Q与圆O、圆P外切，且与BC边相切；

圆S与圆O、圆P、圆Q外切。

证明圆O、圆P、圆Q的半径分别为 ${\frac {1}{\sqrt {3}}}$ 、 ${\frac {1}{3{\sqrt {3}}}}$ 、 ${\frac {2{\sqrt {3}}-3}{6}}$ 。
求圆S半径。

关于《佛临涅槃记法住经》

这部佛经在一些资料中，有提到玛哈帕布和摩诃真言的内容[1]：

“我涅槃后，第二十五百年，有真佛出，名摩诃波菩。金色相好，另立正法，非假佛名。于城邑、郡县、村落、舍宅处，广诵摩诃神咒。慎守禁戒，普化众生。是法恒常极乐，真我清净。”

我去看了下维基文库以及CBETA的全文，根本就没有这段，怀疑是后人阿奎的信徒篡改。--Thyj (คุย) 2024年5月4日 (六) 13:27 (UTC)

中国七十年代末就可以移民美国了吗？

中国七十年代末就可以移民美国了吗？我见过一些人79就移民美国了，从文革走出来立马就那么松了吗？--Wjjksjzs（留言） 2024年5月4日 (六) 15:40 (UTC)

奥林匹亚、奥林匹克的差别？

看到国际科学奥林匹亚这个条目，想请问一下奥林匹亚、奥林匹克有差别吗？还是只是翻译的问题？（但我看表格里的英文都是写Olympiad）谢谢。----　小小泽　　(留言)(签名) 2024年5月4日 (六) 09:55 (UTC)

奥林匹亚的英语是Olympiad，奥林匹克的英语是Olympic。

Olympiad原意见奥林匹亚周期，现在也用来称呼类似奥林匹克的竞赛。--Miyakoo（留言） 2024年5月4日 (六) 19:26 (UTC)

那所以我应该把这些比赛的中文都改成“奥林匹克”？

你点进去看就会发现英文都是Olympiad，中文却有所不同，是否应修改？----　小小泽　　(留言)(签名) 2024年5月4日 (六) 23:38 (UTC)

不用改吧，我搜寻了一下。

大陆一般是奥林匹克竞赛，台湾一般是奥林匹亚竞赛。

搜狐奥林匹克竞赛

台大奥林匹亚竞赛

台湾国教署奥林匹亚竞赛

所以应该算是地区词。--Miyakoo（留言） 2024年5月5日 (日) 00:55 (UTC)

此条目也是将奥林匹克和奥林匹亚当地区词处理的，只不过有几个没转换到。--Miyakoo（留言） 2024年5月5日 (日) 01:16 (UTC)

喔，原来如此，了解了，谢谢！----　小小泽　　(留言)(签名) 2024年5月5日 (日) 01:28 (UTC)

全球华人数量

华人是全球数量最多的族群，想请问近年统计的各国华人的数量是多少人（包含本国和中国香港、中国台湾的人在日韩、东南亚、欧美各国的华人统计）--60.250.103.252（留言） 2024年5月5日 (日) 00:34 (UTC)

台湾就台湾，没有“中国台湾”，就好像没有“中国新加坡”、“中国奥地利”、“中国阿根廷”一样。-游蛇脱壳/克劳棣 2024年5月5日 (日) 04:35 (UTC)

大陆人说中国台湾很正常。--mije meli carrot_233 -- 讨论 2024年5月5日 (日) 04:51 (UTC)

"60.250.0.0 - 60.251.255.255" 都是 Hinet IP，应该不会是大陆人 --Innova（留言） 2024年5月6日 (一) 00:51 (UTC)

也可能是挂绳子的？——Sakamotosan路过围观 | 避免做作，免敬 2024年5月6日 (一) 06:37 (UTC)

首先你如果定义华人，是文化上，还是血源上？

如果你说的是文化上，基本上整个亚洲都受儒家文化的影响。

如果你说的是血源上，我建议你研究一下华人、唐人、汉人这些词语是如何产生的；也建议你研究一下，同一个省不同人种，例如广东省的广州人、梅州人、潮州人之间的差异，跟欧洲不同国家人种之间的差异还要大。--Stanleykswong（留言） 2024年5月5日 (日) 07:39 (UTC)

1.不一定有中国国籍

2.中国的海外公民

3.唐人汉人闽人粤人都好

4.没有多余时间研究，谢谢--60.250.103.252（留言） 2024年5月5日 (日) 10:53 (UTC)

跟闽人、粤人相比，其实唐人、汉人只是一个文化概念，血源关系不大。将几个血源关系不大的民族做分析、研究，其实毫无意义。--Stanleykswong（留言） 2024年5月6日 (一) 09:00 (UTC)

是想做为无国家民族条目的参考资料协助佐证用 !?? --Innova（留言） 2024年5月7日 (二) 01:53 (UTC)

流量密码, 是什么?

zh:流量密码``--Guw Foiursanm Longum（留言） 2024年5月8日 (三) 07:11 (UTC)

see this--YF dyh000（留言） 2024年5月8日 (三) 07:16 (UTC)

“流量密码”是一个网络用语，简单而言就是获得大量点击的方法。增加点击量的主要目的是增加广告收入。--Stanleykswong（留言） 2024年5月9日 (四) 07:27 (UTC)

伊东佑亨致丁汝昌劝降书中的“法国前总统‘末古末哑恒’”是谁

“法国前总统末古末哑恒曾降敌国，以待时机；厥后归助本国政府，更革前政，而法国未尝加以丑辱，且仍推为总统。土耳其之哑司末恒拔香，夫加那利一败，城陷而身为囚虏。一朝归国，即跻大司马之高位，以成改革军制之伟勋，迄未闻有挠其大谋者也。”我现在破译出“哑司末恒拔香”系伊斯麦尔·恩维尔帕夏，惟“末古末哑恒”未解，请各位分析。—— 　桁霁　 ↹　晚来天欲雪，能饮一杯无　　 2024年5月8日 (三) 14:13 (UTC)

按照时间算一定是费利克斯·福尔之前的法国元首。--Mys_721tx（留言） 2024年5月8日 (三) 16:30 (UTC)

按照经历是帕特里斯·麦克马洪。--Mys_721tx（留言） 2024年5月8日 (三) 16:35 (UTC)

应是麦克马洪无疑，“末古”对 Mac，“末哑恒”对 Mahon。深表谢忱，阁下真乃神人也。—— 　桁霁　 ↹　晚来天欲雪，能饮一杯无　　 2024年5月8日 (三) 17:02 (UTC)

明治28年就是公元1895年，当年的法国总统是 Jean Casimir-Perier，他是法国的第六任总统。在他之前有5位前总统，分别是Marie François Sadi Carnot、Jules Grévy、Patrice de Mac Mahon、Adolphe Thiers 和 Louis-Napoléon Bonaparte。而拼音接近的只有 Mac Mahon，所以“末古末哑恒”应该是指 Patrice de Mac Mahon。

而 Patrice de Mac Mahon 的确曾降敌国，在1870年，他率领法军对抗德军失败，向德国人投降，令到当时的皇帝拿破仑三世要流亡国外。--Stanleykswong（留言） 2024年5月9日 (四) 07:46 (UTC)

ipv6 and open-proxy

您好，有谁知道如何检查IPV6地址是否被开放代理使用？对于IPV4，有很多数据库，那么IPV6呢？ -Lemonaka 2024年5月8日 (三) 01:19 (UTC)

IPv6开放代理常见吗。需要计算范围吧。地址范围大、出入口可能不同，怀疑很难收集。--YF dyh000（留言） 2024年5月8日 (三) 02:04 (UTC)

“"被"开放代理使用”是什么意思？是指你的 ISP提供 IPv4转换到IPv6 的功能吗？还是你怀疑自己的电脑已经成为僵尸电脑 ?--Innova（留言） 2024年5月8日 (三) 11:25 (UTC)

维基百科:Open proxy detection这种--YF dyh000（留言） 2024年5月8日 (三) 12:18 (UTC)

Proxy服务是要自己安装程式才能使用，自己的电脑自己有没有安装Proxy服务自己不晓得？如果是要自己扫IPv6, 可以参考这里! 如果是想要借由别人提供的 proxy服务出去, 目前没有看到有人在帮忙扫Free IPv6 Proxy服务机器--Innova（留言） 2024年5月9日 (四) 04:51 (UTC)

他是想侦测某个IP出口是否来自（存在）公开分享的代理服务。--YF dyh000（留言） 2024年5月9日 (四) 05:37 (UTC)

无论任何OS预设都是不会启用Proxy服务的！网络上提供免费Proxy的，大多是自己安装的服务；不存在‘ *被* 开放代理’！

所以我才问他是不是想要知道自己的电脑是不是被入侵被开了后门~ *被* 开启免费代理服务 --Innova（留言） 2024年5月9日 (四) 06:31 (UTC)

IP地址又不可能主动让开放代理使用。

“被开放代理使用”没问题吧。--Miyakoo（留言） 2024年5月9日 (四) 18:28 (UTC)

正是因为这动作不可能 "被动" 处理，所以才搞不清楚原po的意思。就像呼吸动作，每个人自出生就自己会做，所以没有人会说：我"被"吸气了一样 !! --Innova（留言） 2024年5月10日 (五) 03:49 (UTC)

应该是想找工具来尝试扫出以IPv6地址作为出口或者入口的开放代理。扫自己的，上面有工具？扫别人的，IPv6网段太大了，没定向去扫可能很低效。——Sakamotosan路过围观 | 避免做作，免敬 2024年5月9日 (四) 09:29 (UTC)

低效+1, IPv4基本上处于不够用阶段，随便找一个IP ping大概都有人用! IPv6则是完全相反情况，ping 10个 IPv6 看能不能找到 1个实际在线上的. --Innova（留言） 2024年5月10日 (五) 03:45 (UTC)

为什么虹尺蛾属的学名是“Acolutha”？

维基百科很多物种文章会解释学名词源，虹尺蛾属一文未载，亦不见于英维 Acolutha，我遍查互联网亦未考究到。但知道有一古希腊文词与之类似，即 ἀκόλουθος (acólouthos)，enwikt 解释为“following, attending”。不知二者有无关连，特此求教。—— 　桁霁　 ↹　晚来天欲雪，能饮一杯无　　 2024年5月11日 (六) 07:46 (UTC)

另外，白尺蛾属的学名为“Asthena”，比“雅典娜 (Athena)”多一个“s”，比“虚弱乏力 (asthenia)”少一个“i”，也是没能查到词源资料。期盼朋友解惑。—— 　桁霁　 ↹　晚来天欲雪，能饮一杯无　　 2024年5月11日 (六) 08:10 (UTC)

圆半径的取值范围

已知有一三角形ABC，AB=8，BC=3，角C=90度，点D在线段AC上，点E在CA的延长线上，且CD=DE，如果圆B过点A，圆E过点D，若圆B和圆E有公共点，求圆E半径r的取值范围.mije meli carrot_233 -- 讨论 2024年5月6日 (一) 08:24 (UTC)

这里是解答任何与维基百科无关的问题的地方，就像图书馆的询问处，或者问答网站之类的服务。提出问题之前，请先在右方搜寻现有条目。发问前，请留意以下重要事项：

请在主题栏简明扼要地写出问题主旨，不要使用如“新问题”等无意义的文字。
请勿公开姓名、地理地址、电话、电子信箱地址等联络资讯。我们通常只在此页回应，并不利用电邮或电话等私下回应。
有关维基百科计划的问题，请往互助客栈相关页面询问。
请勿在此页宣扬个人主张或就某个议题发起讨论，此页面仅回答个人不懂的问题。
请勿在此页反复提出相似的问题、寻求代做功课、征求医疗建议或法律意见。

--August0422（留言） 2024年5月7日 (二) 08:32 (UTC)

~~::首先，观察题目中的几何条件：~~

1. 三角形ABC，其中AB=8，BC=3，且角C=90度。

2. 点D在边AC上，点E在CA的延长线上，且CD=DE。

3. 圆B过点A，圆E过点D。

根据这些条件，我们可以进行以下推理和分析：

- 由于ABC是直角三角形，我们可以利用三角形的性质计算出AC的长度。

- 点E在AC的延长线上，且CD=DE，这意味着CE是三角形ACE的中位线，因此CE等于AC的一半。

- 由于圆B过点A，其半径即为AB的长度。

- 由于圆E过点D，其半径即为DE的长度。

根据勾股定理，我们可以计算出AC的长度：

\[ AC = \sqrt{AB^2 + BC^2} = \sqrt{8^2 + 3^2} = \sqrt{73} \]

因此，CE的长度为AC的一半，即 $ CE = \frac{1}{2} \sqrt{73} $。

因为CD=DE，所以 $ CD = DE = \frac{1}{2} \sqrt{73} $。

现在，我们可以通过圆B和圆E是否有公共点来确定圆E的半径r的取值范围。如果圆B和圆E有公共点，则圆E的半径r必须满足以下条件之一：

1. 圆E的半径r小于等于CE的长度，即 $ r \leq \frac{1}{2} \sqrt{73} $。

2. 圆E的半径r小于等于CD的长度，即 $ r \leq \frac{1}{2} \sqrt{73} $。

~~综上所述，圆E的半径r的取值范围为 $ 0 < r \leq \frac{1}{2} \sqrt{73} $。--August0422（留言） 2024年5月7日 (二) 08:33 (UTC)~~

你AC的长度就算错了，B不是直角，C才是直角。而且你全部忘了加<math></math>，数学式是显示不出来的，只看得到源代码。-游蛇脱壳/克劳棣 2024年5月7日 (二) 09:11 (UTC)

他这一看就是ChatGPT写的。--mije meli carrot_233 -- 讨论 2024年5月7日 (二) 10:30 (UTC)

答案是不是

{\frac {\sqrt {55}}{2}}\leq r\leq {\frac {8+{\sqrt {229}}}{3}}

？-游蛇脱壳/克劳棣 2024年5月7日 (二) 14:36 (UTC)

@Carrot2333君：阁下是不是忘了问过这个问题？否则怎么这么久无任何回应？-游蛇脱壳/克劳棣 2024年5月12日 (日) 09:14 (UTC)

第一拉格朗日点

请问有人可以告诉我拉格朗日点 $L_{1}$ 的距离公式是怎么推出来的吗？条目中写得不太清楚，不知道列式是怎么来的。----　小小泽　　(留言)(签名) 2024年5月14日 (二) 11:37 (UTC)

因子

{\sqrt[{3}]{\frac {1}{3}}}

似乎是在高阶展开下得到的，建议找本教材看看。--Heihaheihaha 麻瓜了……（留言） 2024年5月19日 (日) 14:28 (UTC)

多普勒效应

我们都知道，除法的分母为零，代表无限大！

多普勒效应公式:

观察者（Observer）和发射源（Source）的频率关系为： $f'=\left({\frac {v\pm v_{\mathrm {o} }}{v\mp v_{\mathrm {s} }}}\right)f$

$f'$ 为观察到的频率；
$f$ 为发射源于该介质中的原始发射频率；
$v$ 为波在该介质中的行进速度；
$v_{\mathrm {o} }$ 为观察者相对于介质的移动速度，若接近发射源则前方运算符号为+号，反之则为−号；
$v_{\mathrm {s} }$ 为发射源相对于介质的移动速度，若接近观察者则前方运算符号为−号，反之则为+号。

如果我在恰好以音速行进中的载具上发出声音，那么, $v_{\mathrm {s} }$ =音速！

$v$ (=音速) - $v_{\mathrm {s} }$ (=音速) ==> 分母为零 !!

那么，在地面的你就会听到 `无限大` 的声音!!!?

这算式有哪里不对吗？

Innova（留言） 2024年5月21日 (二) 07:57 (UTC)

不是听到“无限大”的声音，而是听到“无限高”的频率（如果你的耳朵有足够带宽，不过正常人的耳朵只能听到20Hz到20000Hz之间的声音）。--Stanleykswong（留言） 2024年5月21日 (二) 17:12 (UTC)

那如果超音速会怎样？频率可以是负数吗？-游蛇脱壳/克劳棣 2024年5月22日 (三) 12:04 (UTC)

那如果是超音速，则速度越高，频率越低，不过最低也不会低于发射源的频率。例如，如果速度是 Mach 2，频率会是发射源频率的三倍，不过如果速度是 Mach 11，频率会跌到发射源频率的一点二倍。--Stanleykswong（留言） 2024年5月22日 (三) 16:51 (UTC)

师兄，我前面的回复有错，超音速的情况比想像中复杂。其实近音速之下，已经很复杂。--Stanleykswong（留言） 2024年5月22日 (三) 17:28 (UTC)

电影片头片尾变化

最近在消化YouTube内的免费电影，专挑IMDB评分高的。发现1960年代左右或更早的电影，片头片尾都非常短，有时甚至不到一分钟，像是只为了留个纪录，并不打算让人看完内容。到后面的电影才越来越长，也卷得越来越慢，让观众看清楚幕前幕后都有谁。有些还加上彩蛋。请问有这种演变的专著吗？有写入条目的价值吗？--2603:8000:500:FB00:A91F:A5ED:3BB9:92F（留言） 2024年5月23日 (四) 03:20 (UTC)

维基百科：青岛市

维基百科并未出现行政区划图--60.250.103.252（留言） 2024年5月23日 (四) 14:35 (UTC)

？青岛市#行政区划不是有吗？如果是显示问题，应移步WP:互助客栈/技术。--自由雨日（留言） 2024年5月23日 (四) 14:43 (UTC)

两题根式的级数求和

$\sum _{k=1}^{18}{\sqrt {1+{1 \over k^{2}}+{1 \over (k+1)^{2}}}}$ =?
$\sum _{k=1}^{18}{\sqrt {{\sqrt {(2k-1)^{2}}}-{\sqrt {(2k-1)^{2}-1}}}}$ =?

---游蛇脱壳/克劳棣 2024年5月18日 (六) 17:01 (UTC)

${\sqrt {1+{\frac {1}{k^{2}}}+{\frac {1}{(k+1)^{2}}}}}={\sqrt {\left(1+{\frac {1}{k}}-{\frac {1}{k+1}}\right)^{2}}}=1+{\frac {1}{k}}-{\frac {1}{k+1}}$ 第二题差不多，换元化简。--Heihaheihaha 麻瓜了……（留言） 2024年5月19日 (日) 14:39 (UTC)

不觉得第二题差不多耶！能否也化简给大家看？谢谢！-游蛇脱壳/克劳棣 2024年5月23日 (四) 16:29 (UTC)

近代中国人物传记开头格式

这是我几年前观察到的现象，以下随机挑选几个条目为例：

清朝以前的中国人
- 辛弃疾：辛弃疾，字幼安，号稼轩居士，山东东路济南府历城县人。
- 耶律迭里特：耶律迭里特，辽朝医学家，字海邻，契丹族。
- 张松溪：张松溪，明嘉靖时浙江鄞县人，著名拳术家。
- 朱珪 (清朝)：朱珪，字石君，顺天府大兴县人，清朝政治人物、学者。

近代当代中国人：
- 周建人：周建人，字松寿，又字乔峰，男，浙江绍兴人，
- 李梦龄：李梦龄，号赐九，男，河北晋县人，中华人民共和国政治人物。
- 张彬 (1931年)：张彬，男，河北正定人，中国人民解放军将领、中国人民解放军中将。
- 张柏楠：张柏楠，男，汉族，黑龙江齐齐哈尔人
- 王斌 (1971年)：王斌，男，汉族，山东肥城人，中华人民共和国政治人物
- 史蜀君：史蜀君，女，北京人，生于四川重庆。中国电影导演，编剧。
- 毕华德：毕华德，男，北京人，中国眼科学家、医学教育家
- 程小蒙：程小蒙，原名程小晋，女，重庆人，中国大陆女演员，毕业于四川师范大学播音与主持专业。

非中国人
- 张菲：张菲，台湾男艺人、主持人，
- 藤原夏姬：藤原夏姫，出生于日本北海道札幌市，为写真偶像、角色扮演者、女同性恋者
- 玛格丽特·比斯：玛格丽特·比斯出生于法国巴黎，是一位法式料理的女厨师，

可以发现到，近代当代中国人传记开头，屡屡可见单独把性别这一个字列出来的写法。当然非此类格式的条目，肯定是比采用此类格式的高出很多，但这种格式好像“只出现在近代当代中国人条目”，清朝以前、以及中国以外的几乎都见不到这种写法。不知道有什么原因，譬如某些传记写作的方式影响了这一区间人物的写法？当然也可能是我看的条目样本太少，或有其他原因？ -KRF（留言） 2024年5月23日 (四) 13:59 (UTC)