Fisisorción

La fisisorción, también llamada adsorción física, es un proceso en el que la estructura electrónica del átomo o molécula apenas se perturba durante la adsorción.[1][2][3]
Introducción
[editar]La fuerza de interacción fundamental de la fisisorción es Van der Waals (VDW). Aunque la energía de interacción es muy débil (~10 – 100 meV), la fisisorción juega un papel importante en la naturaleza. Por ejemplo, la atracción de van der Waals entre las superficies y los pelos de los geckos proporciona la notable capacidad de trepar por paredes verticales.[4] Las fuerzas de Van der Waals se originan a partir de las interacciones entre dipolos eléctricos inducidos, permanentes o transitorios.
En comparación con la quimisorción, en la que la estructura electrónica de los átomos o moléculas enlazantes cambia y se forman enlaces covalentes o iónicos, la fisisorción no produce cambios en la estructura de los enlaces químicos. En la práctica, la categorización de una adsorción particular como fisisorción o quimisorción depende principalmente de la energía de unión del adsorbato al sustrato, siendo la fisisorción mucho más débil por átomo que cualquier tipo de conexión que implique un enlace químico.
Modelado por carga de imagen
[editar]
Para dar una ilustración simple de fisisorción, primero podemos considerar un átomo de hidrógeno adsorbido frente a un conductor perfecto, como se muestra en la Fig.1. Un núcleo con carga positiva se encuentra en R = (0, 0, Z), y la coordenada de posición de su electrón, r = (x, y, z) se da con respecto al núcleo. El proceso de adsorción puede verse como la interacción entre este átomo de hidrógeno y sus cargas de imagen tanto del núcleo como del electrón en el conductor. Como resultado, la energía electrostática total es la suma de los términos de atracción y repulsión:
El primer término es la interacción atractiva del núcleo y su carga de imagen, y el segundo término se debe a la interacción del electrón y su carga de imagen. La interacción repulsiva se muestra en el tercer y cuarto términos que surgen de la interacción entre el núcleo y el electrón de la imagen, y la interacción entre el electrón y el núcleo de la imagen, respectivamente.
Por expansión de Taylor en potencias de |r|/|R|, esta energía de interacción se puede expresar además como:
A partir del primer término que no desaparece, se puede encontrar que el potencial de fisisorción depende de la distancia Z entre el átomo adsorbido y la superficie como Z − 3, en contraste con la dependencia r − 6 del potencial molecular de van der Waals, donde r es la distancia entre dos dipolos.
Modelado por oscilador mecánico cuántico
[editar]La energía de enlace de van der Waals se puede analizar mediante otra imagen física simple: modelar el movimiento de un electrón alrededor de su núcleo mediante un oscilador armónico simple tridimensional con una energía potencial Va:
donde me y ω son la masa y la frecuencia vibratoria del electrón, respectivamente.
A medida que este átomo se acerca a la superficie de un metal y forma adsorción, esta energía potencial V a se modificará debido a las cargas de la imagen por términos potenciales adicionales que son cuadráticos en los desplazamientos:
- (de la expansión de Taylor anterior. )
Asumiendo
el potencial está bien aproximado como
- ,
donde
Si se supone que el electrón está en el estado fundamental, entonces la energía de enlace de van der Waals es esencialmente el cambio de la energía del punto cero:
Esta expresión también muestra la naturaleza de la dependencia Z −3 de la interacción de van der Waals.
Además, al introducir la polarización atómica,
el potencial de van der Waals se puede simplificar aún más:
donde
es la constante de van der Waals que está relacionada con la polarizabilidad atómica.
Además, al expresar la corrección de cuarto orden en la expansión de Taylor anterior como (aCvZ0)/(Z4), donde a es una constante, podemos definir Z0 como la posición del plano de la imagen dinámica y obtener
| Él | Ne | Ar | Kr | Xe | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| C v | Z0 | Cv | Z0 | Cv | Z0 | Cv | Z0 | Cv | Z0 | |
| Cu | 0,225 | 0,22 | 0.452 | 0,21 | 1.501 | 0,26 | 2.11 | 0,27 | 3.085 | 0,29 |
| Ag | 0,249 | 0,2 | 0.502 | 0,19 | 1.623 | 0,24 | 2.263 | 0,25 | 3.277 | 0,27 |
| Au | 0,274 | 0,16 | 0.554 | 0,15 | 1.768 | 0,19 | 2.455 | 0,2 | 3.533 | 0,22 |
El origen de Z 0 proviene del derrame de la función de onda del electrón fuera de la superficie. Como resultado, la posición del plano de la imagen que representa la referencia para la coordenada espacial es diferente de la propia superficie del sustrato y está modificada por Z0.
La Tabla 1 muestra el cálculo del modelo de gelatina para la constante Cv de van der Waals y el plano de imagen dinámica Z 0 de átomos de gas raro en varias superficies metálicas. El aumento de Cv de He a Xe para todos los sustratos metálicos es causado por la mayor polarización atómica de los átomos de gas raro más pesados. Para la posición del plano de la imagen dinámica, disminuye al aumentar la función dieléctrica y suele ser del orden de 0,2 A.
Potencial de fisisorción
[editar]
Aunque la interacción de van der Waals es atractiva, a medida que el átomo adsorbido se acerca a la superficie, la función de onda del electrón comienza a superponerse con la de los átomos de la superficie. Además, la energía del sistema aumentará debido a la ortogonalidad de las funciones de onda del átomo que se aproxima y los átomos de la superficie.
Esta exclusión y repulsión de Pauli son particularmente fuertes para los átomos con capas de valencia cerradas que dominan la interacción de la superficie. Como resultado, la energía mínima de fisisorción debe encontrarse mediante el equilibrio entre la atracción de van der Waals de largo alcance y la repulsión de Pauli de corto alcance. Por ejemplo, al separar la interacción total de la fisisorción en dos contribuciones (un término de corto alcance representado por la teoría de Hartree-Fock y una atracción de van der Waals de largo alcance) se puede determinar la posición de equilibrio de la fisisorción de gases raros adsorbidos en un sustrato de gelatina.[5] La Fig. 2 muestra la energía potencial de fisisorción de He adsorbido en sustratos de Ag, Cu y Au que se describen mediante el modelo de gelatina con diferentes densidades de cargas positivas de fondo difuminadas. Se puede encontrar que la interacción débil de van der Waals conduce a pozos de energía atractivos poco profundos (<10 meV). Uno de los métodos experimentales para explorar la energía potencial de fisisorción es el proceso de dispersión, por ejemplo, átomos de gas inerte dispersos de superficies metálicas. Ciertas características específicas del potencial de interacción entre los átomos dispersos y la superficie se pueden extraer analizando la distribución angular determinada experimentalmente y las secciones transversales de las partículas dispersas.
Mecánica cuántica: modelado termodinámico para área de superficie y porosidad
[editar]Desde 1980 se trabajaron dos teorías para explicar la adsorción y obtener ecuaciones que funcionen. Estos dos se conocen como la hipótesis chi, la derivación de la mecánica cuántica y el exceso de trabajo superficial, ESW.[6] Ambas teorías producen la misma ecuación para superficies planas:
Donde U es la función de paso unitario. Las definiciones de los otros símbolos son las siguientes:
donde "ads" significa "adsorbido", "m" significa "equivalencia de monocapa" y "vap" es una referencia a la presión de vapor del adsorbente líquido a la misma temperatura que la muestra sólida. La función unitaria crea la definición de la energía molar de adsorción para la primera molécula adsorbida mediante:
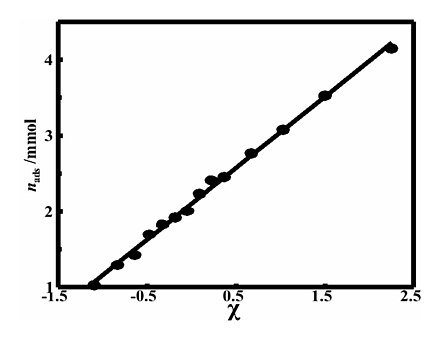
La trama de adsorbido versus se conoce como la gráfica chi. Para superficies planas, la pendiente de la gráfica chi produce el área de superficie. Empíricamente,[7][8][9][10] se demostró que esta trama encajaba muy bien con la isoterma, pero no se siguió. Esta ecuación de superficie plana puede usarse como una "curva estándar" en la tradición normal de curvas de comparación, con la excepción de que la parte inicial de la muestra porosa de la gráfica de versus actúa como un estándar propio. Las condiciones ultramicroporosas, microporosas y mesoporosas pueden analizarse utilizando esta técnica. Las desviaciones estándar típicas para ajustes de isotermas completos, incluidas las muestras porosas, suelen ser inferiores al 2%.
En la figura 3 se muestra un ajuste típico a buenos datos en una superficie no porosa homogénea.[11] A diferencia de BET, que solo puede ajustarse mejor en el rango de 0.05 a 0.35 de P/P vap, el rango de ajuste es la isoterma completa.
Comparación con quimisorción
[editar]- La fisisorción es un fenómeno general y ocurre en cualquier sistema sólido/fluido o sólido/gas. La quimisorción se caracteriza por la especificidad química.
- En la fisisorción, la perturbación de los estados electrónicos de adsorbente y adsorbato es mínima. Las fuerzas de adsorción incluyen las fuerzas de London, las atracciones dipolo-dipolo, la atracción inducida por dipolo y el "enlace de hidrógeno". Para la quimisorción, los cambios en los estados electrónicos pueden detectarse mediante medios físicos adecuados, en otras palabras, enlaces químicos.
- Energía de unión típico de fisisorción es de aproximadamente 10 a – meV y no localizada. La quimisorción por lo general forma de unión con la energía de 1 – 10 eV y localizado.
- El paso elemental en la fisisorción de una fase gaseosa no implica una energía de activación. La quimisorción a menudo implica una energía de activación.
- Para las moléculas en fase gaseosa de fisisorción, los adsorbatos forman una adsorción multicapa a menos que interfieran barreras físicas, como la porosidad. En la quimisorción, las moléculas se adsorben en la superficie por enlaces de valencia y solo forman adsorción en monocapa.
- Se ha observado una transición directa de la fisisorción a la quimisorción al unir una molécula de CO a la punta de un microscopio de fuerza atómica y medir su interacción con un solo átomo de hierro.[12]
Véase también
[editar]Referencias
[editar]- ↑ K. Oura (2003), Surface Science, An Introduction, Berlin: Springer, ISBN 978-3-540-00545-2.
- ↑ M. C. Desjonqueres (1996), Concepts in surface physics (2nd edición), New York: Springer-Verlag, ISBN 978-3-540-58622-7, consultado el 29 de agosto de 2012.
- ↑ Hans Luth (1993), Surfaces and interfaces of solids, Springer-Verlag, ISBN 978-3-540-56840-7.
- ↑ K. Autumn (2000), «Adhesive force of a single gecko foot-hair», Nature 405 (6787): 681-5, Bibcode:2000Natur.405..681A, PMID 10864324, doi:10.1038/35015073.
- ↑ a b E. Zaremba and W. Kohn (1977), «Theory of helium adsorption on simple and noble-metal surfaces», Phys. Rev. B 15 (4): 1769-1781, Bibcode:1977PhRvB..15.1769Z, doi:10.1103/PhysRevB.15.1769.
- ↑ Condon, James (2020). Surface Area and Porosity Determinations by Physisorption, 2nd edition. Measurement, Classical Theory and Quantum Theory. Amsterdam.NL: Elsevier. pp. Chapters 3, 4 and 5. ISBN 978-0-12-818785-2.
- ↑ Polanyi, M. (1914). Verk. Deutsch. Physik, Gas 16: 1012.
- ↑ Polanyi, M. (1920). «Neueres über Adsorption und Ursache der Adsorptionskräfte». Z. Electrochem. 26: 370-374.
- ↑ Polanyi, M. (1929). «Grundlagen der Potentialtheorie der Adsorption». Z Electrohem. 35: 431-432.
- ↑ deBoer, J.H.; Zwikker, C. (1929). «Adsorption als Folge von Polarisation». Z. Phys. Chem. B3: 407-420.
- ↑ Payne, D. A.; Sing, K. S. W.; D. H. Turk (1973). «Comparison of argon and nitrogen adsorption isotherms on porous and nonporous hydroxylated silica». J. Colloid Interface Sci. 43: 287.
- ↑ Huber, Ferdinand; Berwanger, Julian; Polesya, Svitlana; Mankovsky, Sergiy; Ebert, Hubert; Giessibl, Franz J. (11 de octubre de 2019). «Chemical bond formation showing a transition from physisorption to chemisorption». Science (en inglés) 366 (6462): 235-238. ISSN 0036-8075. doi:10.1126/science.aay3444.

















