Trisectriz de Ceva
La trisectriz de Ceva,[1] también conocida como cicloide de Ceva, es una curva plana que lleva el nombre de Tommaso Ceva (1648-1736), y que se puede utilizar para la trisección de un ángulo arbitrario (de ahí el nombre de trisectriz). El propio Ceva se refirió a la curva como cycloidum anomalarum.
Definición geométrica
[editar]

(triángulo isósceles)
(teorema del ángulo exterior, conjunto básico de ángulos)
(ángulo, suma de ángulos)
Para un punto de la circunferencia goniométrica se construye la línea recta que conecta el punto con el origen . Luego, se determina sobre el eje x el punto , que tiene una distancia de 1 desde . Finalmente, se determina entonces el punto como la intersección (distinta del punto ) de la línea recta con la circunferencia de radio 1 y centro . La cicloide de Ceva es ahora el lugar geométrico de los puntos , que se obtiene rotando el punto y por lo tanto también la línea recta , alrededor del origen .
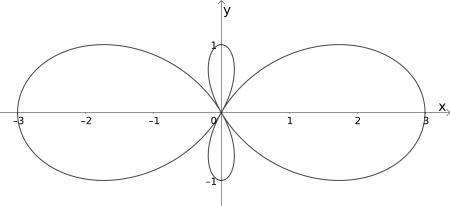
El lugar geométrico consta de cuatro bucles axialmente simétricos en el origen, siendo los dos bucles del eje x significativamente más grandes que los dos del eje y. Si solo se usa la semirrecta en lugar de la recta, entonces se omiten los dos pequeños bucles en el eje y.
Debido a su construcción, el ángulo entre la línea recta y el eje x es exactamente un tercio del ángulo entre la línea y el eje x (véase el dibujo). Debido a esta propiedad, la curva se puede utilizar como una trisectriz.
Si se continúa el proceso de construcción de los puntos , y para otros puntos , se obtienen curvas del lugar geométrico de que son sectrices de Ceva para =impar.
Forma de la ecuación y parámetro
[editar]La siguiente ecuación en coordenadas polares[1] se puede deducir de la definición geométrica con la ayuda del teorema del coseno:
- .
La siguiente representación se obtiene como la curva de parámetros[1] en coordenadas cartesianas:
- .
Además, la siguiente ecuación da como resultado coordenadas cartesianas, comprobándose que la cicloide de Ceva es una curva algebraica de sexto grado:[2]
- .
Trisección angular
[editar] |
 |
La propiedad angular de las cicloides de Ceva descrita anteriormente proporciona la siguiente construcción para dividir un ángulo en tres partes iguales.[1] En un ángulo dado , primero extender el cateto y dibujar la cicloide con como eje x. Luego, en el otro cateto , dibujar la línea con longitud 1 y dibujar una paralela a a través del punto . Esta recta se cruza con la cicloide en el punto . Ahora, conectar el punto con el centro de la cicloide (origen del sistema de coordenadas), luego la línea con la extensión de forma un ángulo cuya dimensión angular es exactamente un tercio de la dimensión angular del ángulo inicial . Téngase en cuenta que en el caso de ángulos agudos u obtusos, la paralela siempre se cruza con la cicloide en dos puntos, por lo que inicialmente hay dos puntos disponibles para determinar . Si es un ángulo agudo (), la intersección más cercana al ángulo se selecciona como . En el caso de un ángulo obtuso () sin embargo, se elige el punto de intersección más distante como .
Tipos de curvas de Ceva
[editar]
Cuando la trisectriz de Ceva se expresa con la forma polar:
variando el parámetro , se obtienen una serie de curvas particulares:[2]
- b=0 >> la curva resultante es una circunferencia
- b=1/8 >> la curva resultante recuerda a la forma de un pomelo
- b=1/4 >> la curva resultante recuerda a la forma de una gragea
- b=1/2 >> la curva resultante recuerda a la forma de un cacahuete
- b=3/4 >> la curva resultante recuerda a la forma de un antifaz
- b=1 >> la curva resultante recuerda a la forma de un doble huevo
- b=2 >> trisectriz de Ceva
- b=4 >> trébol de cuatro hojas iguales dos a dos
- b=16 >> trébol de cuatro hojas de la misma longitud
Sectriz de Ceva
[editar]
La curva de orden n, con ecuación polar:[1]
es una -sectriz, y se denomina sectriz de Ceva.
Historia
[editar]Tommaso Ceva (1648-1736), hermano de Giovanni Ceva (1647-1734), describió la curva en su obra Opuscula mathica publicada en 1699, obra en la que la curva apareció denominada como cycloidum anomalarum. La idea matemática en la que se basa la construcción de la curva se remonta a Arquímedes (287-212 a. C.), quien la utilizó para realizar la trisección del ángulo con la ayuda de una regla marcada.
Referencias
[editar]- ↑ a b c d e «CEVA TRISECTRIX AND SECTRIX». mathcurve (en inglés). Consultado el 16 de marzo de 2021.
- ↑ a b «(extended) Ceva's trisectrix». 2dcurves (en inglés). Consultado el 16 de marzo de 2021.
Bibliografía
[editar]- Gino Loria: Spezielle algebraische und transscendente Ebene Kurven: Theorie und Geschichte. Teubner, 1902, S. 324–325
- Eugene V. Shikin: Handbook and Atlas of Curves. CRC Press, 1996, ISBN 9780849389634, S. 315
- Robert C. Yates: The Trisection Problem. National Mathematics Magazine, Band 15, Nr. 4 (Jan., 1941), S. 191–202 (JSTOR)
- Robert C. Yates: The Trisection Problem. Classics in Mathematics Education Series Volume 3, The National Teachers of Mathematics, Education Resources Information Center, 1971, S. 39–40 (Online-Kopie)
- Laszlo Nemeth: Sectrix Curves on the Sphere. KOG 19, Dezember 2015, S. 42–47
- Tommaso Ceva: Opuscula mathematica. Mailand, 1699, S. 31 (Online-Kopie)
Enlaces externos
[editar] Wikimedia Commons alberga una categoría multimedia sobre Trisectriz de Ceva.
Wikimedia Commons alberga una categoría multimedia sobre Trisectriz de Ceva.- Weisstein, Eric W. «Cycloid of Ceva». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Trisección usando curvas especiales
- La división angular en tres partes (construcción con ayudas adicionales) Archivado el 26 de junio de 2002 en Wayback Machine.
- Ceva Trisectriz y Sectriz en mathcurve.com













![{\displaystyle \gamma :[0,2\pi ]\rightarrow \mathbb {R} ^{2}}](https://wikimedia.org/eswiki/api/rest_v1/media/math/render/svg/bea32becc154f483bda6d73f47426b17ddd93952)













