Распределение Райса: различия между версиями
Перейти к навигации
Перейти к поиску
| [отпатрулированная версия] | [отпатрулированная версия] |
Содержимое удалено Содержимое добавлено
Функция «Добавить ссылку»: добавлено 2 ссылки. Метки: через визуальный редактор с мобильного устройства из мобильной версии Задача для новичков предложение: добавить ссылки |
м Форматирование дат согласно Википедия:Техническое соглашение о датах и времени и Википедия:Обсуждение правил/Википедия:Техническое соглашение о датах и времени |
||
| Строка 42: | Строка 42: | ||
{{math-stub}} |
{{math-stub}} |
||
{{нет сносок|дата= |
{{нет сносок|дата=2021-05-31}} |
||
{{Список вероятностных распределений}} |
{{Список вероятностных распределений}} |
||
Текущая версия от 20:47, 21 ноября 2023
| Распределение Райса | |
|---|---|
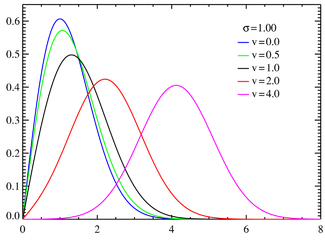 Плотность распределения Райса для различных значений параметра ν при σ = 1. 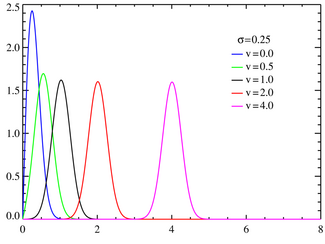 Плотность распределения Райса для различных значений параметра ν при σ = 0.25.Плотность вероятности | |
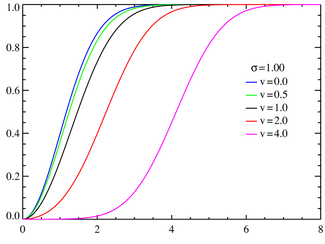 Функция распределения Райса для различных значений параметра ν при σ = 1. 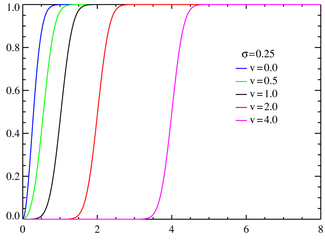 Функция распределения Райса для различных значений параметра ν при σ = 0.25.Функция распределения | |
| Параметры |
|
| Носитель | x ∈ [0, +∞) |
| Плотность вероятности | |
| Функция распределения |
где Q1 - это Q-функция Маркума |
| Математическое ожидание | |
| Дисперсия | |
Распределение Райса является обобщением распределения Рэлея. Введено американским учёным Стефаном Райсом.
Если и — независимые случайные величины, имеющие нормальное распределение с одинаковыми дисперсиями и ненулевыми математическими ожиданиями (в общем случае неравными), то величина имеет распределение Райса, плотность вероятности которой определяется в виде
где I0(z) — модифицированная функция Бесселя первого рода нулевого порядка, , и — математические ожидания и .
Применение
[править | править код]- Распределение Райса часто используют для описания амплитудных флуктуаций радиосигнала, в том числе в многолучевых каналах распространения радиосигнала.
Связь с другими распределениями
[править | править код]- Если и — независимые случайные величины, имеющие нормальное распределение с нулевыми математическими ожиданиями и одинаковыми дисперсиями , то случайная величина имеет распределение Рэлея.
См. также
[править | править код]Литература
[править | править код]- Перов, А. И. Статистическая теория радиотехнических систем. — М.: Радиотехника, 2003. — 400 с. — ISBN 5-93108-047-3.
Это заготовка статьи по математике. Помогите Википедии, дополнив её. |
В статье есть список источников, но не хватает сносок. |
















