W-функция Ламберта: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
NapalmBot (обсуждение | вклад) м Удаление принудительных пробелов в формулах по ВП:РДБ. |
м →Ссылки |
||
| (не показано 45 промежуточных версий 27 участников) | |||
| Строка 1: | Строка 1: | ||
{{DISPLAYTITLE:''W''-функция Ламберта}} |
|||
'''<math>W</math>-функция Ламберта''' определяется как [[обратная функция]] к <math>f(w)=w e^w</math>, для [[Комплексное число|комплексных]] <math>w</math>. Обозначается <math>W(x)</math> или <math>\operatorname{LambertW}(x)</math>. Для любого комплексного <math>z</math> она определяется функциональным уравнением: |
'''<math>W</math>-функция Ламберта''' определяется как [[обратная функция]] к <math>f(w)=w e^w</math>, для [[Комплексное число|комплексных]] <math>w</math>. Обозначается <math>W(x)</math> или <math>\operatorname{LambertW}(x)</math>. Для любого комплексного <math>z</math> она определяется [[Функциональное уравнение|функциональным уравнением]]: |
||
:<math>z=W(z |
: <math>z=W(z e^{z})</math> |
||
<math>W</math>-функция Ламберта не может быть выражена в [[элементарные функции|элементарных функциях]]. Она применяется в [[комбинаторика|комбинаторике]], например, при подсчёте числа [[дерево (граф)|деревьев]], а также при решении уравнений. |
<math>W</math>-функция Ламберта не может быть выражена в [[элементарные функции|элементарных функциях]]. Она применяется в [[комбинаторика|комбинаторике]], например, при подсчёте числа [[дерево (граф)|деревьев]], а также при решении уравнений. |
||
== История == |
== История == |
||
Функция изучалась ещё в работе [[Эйлер, Леонард|Леонарда Эйлера]] |
Функция изучалась ещё в работе [[Эйлер, Леонард|Леонарда Эйлера]] [[1779 год|1779-го года]], но не имела самостоятельного значения и названия вплоть до 1980-х годов. Как самостоятельная функция была введена в системе компьютерной алгебры [[Maple]], где для неё использовалось имя '''LambertW'''. Имя [[Ламберт, Иоганн Генрих|Иоганна Генриха Ламберта]] было выбрано, поскольку Эйлер ссылался в своей работе на труды Ламберта, и поскольку «называть ещё одну функцию именем Эйлера было бы бесполезно»<ref name="Corless">{{статья |ссылка=http://www.apmaths.uwo.ca/~djeffrey/Offprints/W-adv-cm.ps |заглавие=On the Lambert W function |издание=Adv. Computational Maths. |том=5 |страницы=329—359 |archiveurl=https://web.archive.org/web/20050118104553/http://www.apmaths.uwo.ca/~djeffrey/Offprints/W-adv-cm.ps |archivedate=2005-01-18 |deadlink=404 |accessdate=2006-09-11 |язык=und |автор=Corless et al. |год=1996}}</ref>. |
||
== Многозначность == |
== Многозначность == |
||
[[Файл:Mplwp lambert W branches.svg|thumb|Основная <math>W_0</math> (синяя) и дополнительная <math>W_{-1}</math> (фиолетовая) ветви функции <math>W(x)</math>]] |
|||
{{обобщить|<math>W_0(x)</math>}} |
|||
[[Файл:Diagram of the real branches of the Lambert W function.png|thumb|Две главные ветви функции <math>W_0</math> и <math>W_{-1}</math>]] |
|||
[[Файл:lambertw.png|thumb|288px|right|График ''W''<sub>0</sub>(''x'') для −1/''e'' ≤ ''x'' ≤ 4]] |
[[Файл:lambertw.png|thumb|288px|right|График ''W''<sub>0</sub>(''x'') для −1/''e'' ≤ ''x'' ≤ 4]] |
||
Поскольку функция <math>f(w)</math> не является [[инъекция (математика)|инъективной]] на интервале <math>(-\infty,0)</math>, <math>W(z)</math> является многозначной функцией на <math> |
Поскольку функция <math>f(w)</math> не является [[инъекция (математика)|инъективной]] на интервале <math>(-\infty,0)</math>, <math>W(z)</math> является [[Многозначная функция|многозначной функцией]] на <math>(-\frac{1}{e},0)</math>. |
||
* Если ограничиться вещественными <math>z = x\geqslant-1/e</math> и потребовать <math>w\geqslant -1</math>, будет определена однозначная функция <math>W_0(x)</math> — основная ветвь функции <math>W(x)</math>. |
|||
* Если ограничиться вещественными <math>z = x\geqslant-1/e</math>, <math>z = x < 0</math> и потребовать <math>w\leqslant -1</math>, будет определена однозначная функция <math>W_{-1}(x)</math> — дополнительная ветвь функции <math>W(x)</math>. |
|||
== Асимптотики == |
== Асимптотики == |
||
Полезно знать асимптотики функции при стремлении к некоторым ключевым точкам. Например, для ускорения сходимости при выполнении рекуррентных |
Полезно знать асимптотики функции при стремлении к некоторым ключевым точкам. Например, для ускорения сходимости при выполнении рекуррентных расчётов. |
||
<math>\left.W(z)\right|_{z \to \infty} = \log(z)-\log( \log(z) )</math> |
<math>\left.W(z)\right|_{z \to \infty} = \log(z)-\log( \log(z) )</math> |
||
| Строка 21: | Строка 23: | ||
== Другие формулы == |
== Другие формулы == |
||
:<math>\int_{0}^{\pi} W\bigl( 2\cot^2(x) \bigr)\sec^2(x)\;\mathrm dx = 4\sqrt{\pi}</math> |
: <math>\int_{0}^{\pi} W\bigl( 2\cot^2(x) \bigr)\sec^2(x)\;\mathrm dx = 4\sqrt{\pi}</math> |
||
:<math>\int_{0}^{+\infty} W\left(\frac{1}{x^2}\right)\;\mathrm dx = \sqrt{2\pi}</math> |
: <math>\int_{0}^{+\infty} W\left(\frac{1}{x^2}\right)\;\mathrm dx = \sqrt{2\pi}</math> |
||
:<math>\int_{0}^{+\infty} \frac{W(x)}{x\sqrt{x}}\mathrm dx = 2\sqrt{2\pi}</math> |
: <math>\int_{0}^{+\infty} \frac{W(x)}{x\sqrt{x}}\mathrm dx = 2\sqrt{2\pi}</math> |
||
== Свойства == |
== Свойства == |
||
С помощью дифференцирования неявной функции можно получить, что при <math>z\ne -\tfrac{1}{e}</math> функция Ламберта удовлетворяет следующему дифференциальному уравнению: |
С помощью дифференцирования неявной функции можно получить, что при <math>z\ne -\tfrac{1}{e}</math> функция Ламберта удовлетворяет следующему дифференциальному уравнению: |
||
:<math>{dW\over dz} = \frac{1}{z} \frac{W(z)}{W(z)+1}.</math> |
: <math>{dW\over dz} = \frac{1}{z} \frac{W(z)}{W(z)+1}.</math> |
||
С помощью [[Теорема об обращении рядов|теоремы об обращении рядов]] можно получить выражение для [[Ряд Тейлора|ряда Тейлора]]; он в окрестности нуля сходится при <math>|z|<\tfrac{1}{e}</math>: |
С помощью [[Теорема об обращении рядов|теоремы об обращении рядов]] можно получить выражение для [[Ряд Тейлора|ряда Тейлора]]; он в окрестности нуля сходится при <math>|z|<\tfrac{1}{e}</math>: |
||
:<math>W_0(x)=\sum_{n=1}^\infty \frac{(-n)^{n-1}}{n!}\ x^n = x - x^2 + \frac{3}{2}x^3 - \frac{8}{3}x^4 + \frac{125}{24}x^5 - \cdots.</math> |
: <math>W_0(x)=\sum_{n=1}^\infty \frac{(-n)^{n-1}}{n!}\ x^n = x - x^2 + \frac{3}{2}x^3 - \frac{8}{3}x^4 + \frac{125}{24}x^5 - \cdots.</math> |
||
С помощью [[интегрирование по частям|интегрирования по частям]] можно найти интеграл от W(z): |
С помощью [[интегрирование по частям|интегрирования по частям]] можно найти интеграл от W(z): |
||
:<math>\int W(x)\, dx = x \left( W(x) - 1 + \frac{1}{W(x)} \right) + C.</math> |
: <math>\int W(x)\, dx = x \left( W(x) - 1 + \frac{1}{W(x)} \right) + C.</math> |
||
=== Значения в некоторых точках === |
=== Значения в некоторых точках === |
||
:<math>W\left(-\frac{\pi}{2}\right) = \frac{i\pi}{2}</math> |
: <math>W\left(-\frac{\pi}{2}\right) = \frac{i\pi}{2}</math> |
||
:<math>W(-1) \approx -0.31813 |
: <math>W(-1) \approx -0.31813+1.33723i</math> |
||
:<math>W\left(-{1\over e}\right) = -1</math> |
: <math>W\left(-{1\over e}\right) = -1</math> |
||
:<math>W\left(-\frac{\ln a}{a}\right)= -\ln a |
: <math>W\left(-\frac{\ln a}{a}\right)= -\ln a</math>, при <math>\frac{1}{e}\le a\le e</math> |
||
:<math>W(0) = 0</math> |
: <math>W(0) = 0</math> |
||
:<math>W(e) = 1</math> |
: <math>W(e) = 1</math> |
||
:<math>W(1) = \Omega \approx 0{,}56714329</math> ([[постоянная Омега]]) |
: <math>W(1) = \Omega \approx 0{,}56714329</math> ([[Постоянная омега|постоянная Омега]]) |
||
=== Формулы === |
|||
| ⚫ | |||
<big><math>W(xe^x)=x, \,x>0</math></big> |
|||
| ⚫ | |||
<big><math>W_0(xe^x)=x, \,x\geqslant-1</math></big> |
|||
<big><math>W_{-1}(xe^x)=x, \,x\leqslant-1</math></big> |
|||
| ⚫ | |||
<big><math>e^{n\cdot W(x)}=\left(\frac{x}{W(x)}\right)^n</math></big> |
|||
<big><math>\ln W(x)=\ln x-W(x), \, x>0</math></big> |
|||
<math>W\left(\frac{nx^n}{W(x)^{n-1}}\right)=nW(x) ,\, n>0,x>0</math> |
|||
Обозначим <math>y=-x\ln 2</math>, тогда <math>y\,e^y={-\ln 2\over 5}</math>, отсюда |
|||
<math>y=W\left({-\ln 2\over 5}\right)</math> и окончательно |
|||
<math>x=-{1\over\ln2}W\left({-\ln 2\over 5}\right)</math>. |
|||
<math>W(x)+W(y)=W\left(xy\left(\frac{W(x)+W(y)}{W(x)W(y)}\right)\right),\, x>0,y>0</math> |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
'''Пример 1:''' <math>x\cdot a^x = b</math> |
|||
| ⚫ | где ''a''<sub>0</sub>, ''c'' и ''r'' являются вещественными константами. Решением такого уравнения является <math> x = r + \frac{1}{c} W( \frac{c\,e^{-c r}}{a_o })</math>. Ниже перечислены некоторые из |
||
| ⚫ | |||
| ⚫ | * Эта функция может быть использована в [[Общая теория относительности|общей теории относительности]] и в [[Квантовая механика|квантовой механике]] ([[Квантовая гравитация|квантовой гравитации]]) в нижних измерениях. В журнале |
||
: |
'''Пример 2:''' <math>x^x = a</math> |
||
: <math>x \cdot \ln x = \ln a</math>, следовательно, <math>{\ln a \over x}= W(\ln a)</math>, откуда <math>x = {\ln a \over W(\ln a)}</math>. |
|||
| ⚫ | :и где константы ''r''<sub>1</sub> и ''r''<sub>2</sub>, являются корнями этого квадратичного многочлена. В данном случае решением этого уравнения является функция с аргументом ''x'' , а ''r''<sub>i</sub> и ''a''<sub>o</sub> являются параметрами этой функции. С этой точки зрения, несмотря на то, что данное |
||
'''Пример 3:''' <math>a^x = b x</math> |
|||
| ⚫ | * Эта функция может быть использована для решения частной задачи внутренних энергий квантовой механики, состоящей в определении относительного движения трёх тел, а именно трёхмерной [[молекулярный ион водорода]]<ref>{{ |
||
: <math>{1\over b} = x a^{-x}</math>, тогда <math>-{\ln a\over b} = -x\ln a \cdot e^{-x\ln a}</math>, следовательно, <math>W\left(-{\ln a\over b}\right) = -x\ln a</math>, откуда <math>x=-{1\over\ln a}W\left(-{\ln a\over b}\right)</math>. |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | Применения W- |
||
| ⚫ | где ''a''<sub>0</sub>, ''c'' и ''r'' являются вещественными константами. Решением такого уравнения является <math> x = r + \frac{1}{c} W\Big( \frac{c\,e^{-c r}}{a_o }\Big)</math>. Ниже перечислены некоторые из обобщённых применений ''W''-функции Ламберта:<ref>{{статья |заглавие=General Relativity and Quantum Mechanics: Towards a Generalization of the Lambert W Function |издание=AAECC (Applicable Algebra in Engineering, Communication and Computing) |том=17 |номер=1 |страницы=41—47 |doi=10.1007/s00200-006-0196-1 |ссылка=http://arxiv.org/abs/math-ph/0607011 |язык=en |тип=journal |автор=T. C. Scott, R. B. Mann |год=2006 |archivedate=2019-06-11 |archiveurl=https://web.archive.org/web/20190611060037/http://arxiv.org/abs/math-ph/0607011 }}</ref><ref>{{статья |заглавие=Asymptotic series of Generalized Lambert W Function |издание=SIGSAM (ACM Special Interest Group in Symbolic and Algebraic Manipulation) |том=47 |номер=185 |страницы=75—83 |ссылка=http://www.sigsam.org/cca/issues/issue185.html |язык=en |тип=journal |автор=T. C. Scott, G. Fee, J. Grotendorst |год=2013 |archivedate=2014-07-14 |archiveurl=https://web.archive.org/web/20140714141751/http://www.sigsam.org/cca/issues/issue185.html }}</ref><ref>{{статья |заглавие=Numerics of the Generalized Lambert W Function |издание=SIGSAM |том=48 |номер=1/2 |страницы=42—56 |ссылка=http://www.sigsam.org/cca/issues/issue188.html |язык=und |автор=T. C. Scott, G. Fee, J. Grotendorst, W.Z. Zhang |год=2014 |archivedate=2014-07-14 |archiveurl=https://web.archive.org/web/20140714205400/http://www.sigsam.org/cca/issues/issue188.html }}</ref> |
||
| ⚫ | * Эта функция может быть использована в [[Общая теория относительности|общей теории относительности]] и в [[Квантовая механика|квантовой механике]] ([[Квантовая гравитация|квантовой гравитации]]) в нижних измерениях. В журнале «[[Classical and Quantum Gravity]]»<ref>{{статья |заглавие=N-body Gravity and the Schrödinger Equation |издание=[[Classical and Quantum Gravity]] |том=24 |номер=18 |страницы=4647—4659 |ссылка=http://arxiv.org/abs/gr-qc/0611144 |doi=10.1088/0264-9381/24/18/006 |язык=en |автор=P. S. Farrugia, R. B. Mann, T. C. Scott |год=2007 |тип=journal |archivedate=2019-04-06 |archiveurl=https://web.archive.org/web/20190406063041/https://arxiv.org/abs/gr-qc/0611144 }}</ref> была представлена ранее неизвестная связь между этими двумя понятиями, где правая сторона уравнения превращается в квадратный [[многочлен]] по переменной ''x'': |
||
:: <math> e^{-c x} = a_o (x-r_1 ) (x-r_2 ) ~~\qquad\qquad(2)</math> |
|||
| ⚫ | : и где константы ''r''<sub>1</sub> и ''r''<sub>2</sub>, являются корнями этого квадратичного многочлена. В данном случае решением этого уравнения является функция с аргументом ''x'' , а ''r''<sub>i</sub> и ''a''<sub>o</sub> являются параметрами этой функции. С этой точки зрения, несмотря на то, что данное обобщённое применение ''W''-функции Ламберта напоминает [[Гипергеометрическая функция|гипергеометрическую функцию]] и функцию «Meijer G», оно принадлежит к другому типу функций. Когда ''r''<sub>1</sub> = ''r''<sub>2</sub>, то обе стороны уравнения (2) могут быть упрощены к уравнению (1), и таким образом общее решение упрощается к стандартной ''W''-функцией. Уравнение (2) показывает определяющие отношения в скалярном поле [[дилатон]]ноя, из чего следует решение задачи измерения линейной гравитации парных тел в 1+1 измерениях (измерение пространства и измерение времени) в случае неравных масс, а также решение задачи [[Туннелирование через дельтообразный потенциал|двумерного стационарного уравнения Шрёдингера]] с потенциалом в виде [[Дельта-функция|дельта-функции Дирака]] для неодинаковых зарядов в одном измерении. |
||
| ⚫ | * Эта функция может быть использована для решения частной задачи внутренних энергий квантовой механики, состоящей в определении относительного движения трёх тел, а именно трёхмерной [[молекулярный ион водорода]]<ref>{{статья |заглавие=New Approach for the Electronic Energies of the Hydrogen Molecular Ion |издание={{Нп3|Chemical Physics (journal)|Chem. Phys.||Chemical Physics (journal)}} |том=324 |страницы=323—338 |doi=10.1016/j.chemphys.2005.10.031 |ссылка=http://arxiv.org/abs/physics/0607081 |язык=en |тип=journal |автор=T. C. Scott, M. Aubert-Frécon, J. Grotendorst |год=2006 |archivedate=2016-01-18 |archiveurl=https://web.archive.org/web/20160118022933/http://arxiv.org/abs/physics/0607081 }}</ref><ref>{{статья |заглавие=Fleshing out the Generalized Lambert W Function |издание=SIGSAM |том=50 |номер=2 |страницы=45—60 |doi=10.1145/2992274.2992275 |язык=und |автор=Maignan, Aude; Scott, T. C. |год=2016}}</ref>. В этом случае правая сторона уравнения (1) (или (2)) теперь становится отношением двух беспредельных многочленов по переменной ''x'': |
||
| ⚫ | |||
| ⚫ | : где ''r''<sub>i</sub> и ''s''<sub>i</sub> константы, а ''x'' является функцией между [[Внутренняя энергия|внутренней энергией]] и расстоянием внутри ядра ''R''. Уравнение (3), а также его упрощённые формы, выраженные в уравнениях (1) и (2), относятся к типу дифференциальных уравнений с запозданием. |
||
| ⚫ | Применения ''W''-функции Ламберта в основных проблемах физики не ограничиваются стандартным уравнением (1), как было недавно показано в областях [[Физика атомов и молекул|атомной, молекулярной и оптической физики]]<ref>{{статья |заглавие=The Nodal Surfaces of Helium Atom Eigenfunctions |издание=[[Physical Review|Phys. Rev. A]] |том=75 |страницы=060101 |doi=10.1103/PhysRevA.75.060101 |язык=en |автор=T. C. Scott, A. Lüchow, D. Bressanini, J. D. Morgan III |год=2007 |тип=journal}}</ref> и критерий «Кейпер-Ли» для [[Гипотеза Римана]]<ref>{{статья |заглавие=The Keiper-Li Criterion for the Riemann Hypothesis and Generalized Lambert Functions|издание=ACM Commun. Comput. Algebra|том=57 |номер=3 |страницы=85-110|doi=10.1145/3637529.3637530|язык=und |автор=R.C. McPhedran; T. C. Scott; Aude Maignan|год=2016}}</ref>. |
||
== Вычисление == |
== Вычисление == |
||
<math>W</math>-функция может быть приблизительно вычислена с помощью рекуррентного соотношения<ref name="Corless"/>: |
<math>W</math>-функция может быть приблизительно вычислена с помощью рекуррентного соотношения<ref name="Corless"/>: |
||
:<math> |
: <math> |
||
w_{j+1}=w_j-\frac{w_j e^{w_j}-z}{e^{w_j}(w_j+1)-\frac{(w_j+2)(w_je^{w_j}-z)} |
w_{j+1}=w_j-\frac{w_j e^{w_j}-z}{e^{w_j}(w_j+1)-\frac{(w_j+2)(w_je^{w_j}-z)} |
||
{2w_j+2}} |
{2w_j+2}} |
||
</math> |
</math> |
||
Пример программы на языке Python: |
Пример программы на языке [[Python]]: |
||
<source lang="python"> |
<source lang="python"> |
||
import math |
import math |
||
| Строка 94: | Строка 111: | ||
def lambertW(x, prec=1e-12): |
def lambertW(x, prec=1e-12): |
||
w = 0 |
w = 0 |
||
for i in |
for i in range(100): |
||
wTimesExpW = w*math.exp(w) |
wTimesExpW = w * math.exp(w) |
||
wPlusOneTimesExpW = (w+1)*math.exp(w) |
wPlusOneTimesExpW = (w + 1) * math.exp(w) |
||
w -= (wTimesExpW-x)/(wPlusOneTimesExpW-(w+2)*(wTimesExpW-x)/(2*w+2)) |
w -= (wTimesExpW - x) / (wPlusOneTimesExpW - (w + 2) * (wTimesExpW - x) / (2 * w + 2)) |
||
if |
if prec > abs((x - wTimesExpW) / wPlusOneTimesExpW): |
||
break |
break |
||
if |
if prec <= abs((x - wTimesExpW) / wPlusOneTimesExpW): |
||
raise Exception |
raise Exception("W(x) не сходится достаточно быстро при x=%f" % x) |
||
return w |
return w |
||
</source> |
</source> |
||
Для приближённого вычисления можно использовать формулу<ref name="QCDINS">[http://www.desy.de/~t00fri/qcdins/texhtml/lambertw/ Double precision function LAMBERTW(X)] в пакете [http://www.desy.de/~t00fri/qcdins/qcdins.html QCDINS]</ref> |
Для приближённого вычисления можно использовать следующую формулу<ref name="QCDINS">[http://www.desy.de/~t00fri/qcdins/texhtml/lambertw/ Double precision function LAMBERTW(X)] {{Wayback|url=http://www.desy.de/~t00fri/qcdins/texhtml/lambertw/ |date=20050902203300 }} в пакете [http://www.desy.de/~t00fri/qcdins/qcdins.html QCDINS] {{Wayback|url=http://www.desy.de/~t00fri/qcdins/qcdins.html |date=20050404002616 }}</ref>. |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
W(x) \approx \left\{ |
W(x) \approx \left\{ |
||
\begin{matrix} |
\begin{matrix} |
||
| Строка 114: | Строка 130: | ||
\right. |
\right. |
||
</math> |
</math> |
||
| ⚫ | |||
== |
== Примечания == |
||
{{примечания}} |
|||
<references/> |
|||
[[Категория:Специальные функции]] |
[[Категория:Специальные функции]] |
||
Текущая версия от 12:13, 7 июня 2024
-функция Ламберта определяется как обратная функция к , для комплексных . Обозначается или . Для любого комплексного она определяется функциональным уравнением:
-функция Ламберта не может быть выражена в элементарных функциях. Она применяется в комбинаторике, например, при подсчёте числа деревьев, а также при решении уравнений.
История
[править | править код]Функция изучалась ещё в работе Леонарда Эйлера 1779-го года, но не имела самостоятельного значения и названия вплоть до 1980-х годов. Как самостоятельная функция была введена в системе компьютерной алгебры Maple, где для неё использовалось имя LambertW. Имя Иоганна Генриха Ламберта было выбрано, поскольку Эйлер ссылался в своей работе на труды Ламберта, и поскольку «называть ещё одну функцию именем Эйлера было бы бесполезно»[1].
Многозначность
[править | править код]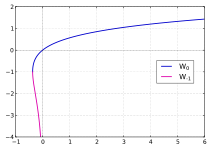

Поскольку функция не является инъективной на интервале , является многозначной функцией на .
- Если ограничиться вещественными и потребовать , будет определена однозначная функция — основная ветвь функции .
- Если ограничиться вещественными , и потребовать , будет определена однозначная функция — дополнительная ветвь функции .
Асимптотики
[править | править код]Полезно знать асимптотики функции при стремлении к некоторым ключевым точкам. Например, для ускорения сходимости при выполнении рекуррентных расчётов.
Другие формулы
[править | править код]Свойства
[править | править код]С помощью дифференцирования неявной функции можно получить, что при функция Ламберта удовлетворяет следующему дифференциальному уравнению:
С помощью теоремы об обращении рядов можно получить выражение для ряда Тейлора; он в окрестности нуля сходится при :
С помощью интегрирования по частям можно найти интеграл от W(z):
Значения в некоторых точках
[править | править код]- , при
- (постоянная Омега)
Формулы
[править | править код]
Решение уравнений с помощью W-функции
[править | править код]Решения многих трансцендентных уравнений могут быть выражены в форме W-функции.
Пример 1:
- , следовательно, , откуда .
Пример 2:
- , следовательно, , откуда .
Пример 3:
- , тогда , следовательно, , откуда .
Обобщённые применения W-функции Ламберта
[править | править код]Стандартная W-функция Ламберта показывает точные решения трансцендентных алгебраических уравнений формы:
где a0, c и r являются вещественными константами. Решением такого уравнения является . Ниже перечислены некоторые из обобщённых применений W-функции Ламберта:[2][3][4]
- Эта функция может быть использована в общей теории относительности и в квантовой механике (квантовой гравитации) в нижних измерениях. В журнале «Classical and Quantum Gravity»[5] была представлена ранее неизвестная связь между этими двумя понятиями, где правая сторона уравнения превращается в квадратный многочлен по переменной x:
- и где константы r1 и r2, являются корнями этого квадратичного многочлена. В данном случае решением этого уравнения является функция с аргументом x , а ri и ao являются параметрами этой функции. С этой точки зрения, несмотря на то, что данное обобщённое применение W-функции Ламберта напоминает гипергеометрическую функцию и функцию «Meijer G», оно принадлежит к другому типу функций. Когда r1 = r2, то обе стороны уравнения (2) могут быть упрощены к уравнению (1), и таким образом общее решение упрощается к стандартной W-функцией. Уравнение (2) показывает определяющие отношения в скалярном поле дилатонноя, из чего следует решение задачи измерения линейной гравитации парных тел в 1+1 измерениях (измерение пространства и измерение времени) в случае неравных масс, а также решение задачи двумерного стационарного уравнения Шрёдингера с потенциалом в виде дельта-функции Дирака для неодинаковых зарядов в одном измерении.
- Эта функция может быть использована для решения частной задачи внутренних энергий квантовой механики, состоящей в определении относительного движения трёх тел, а именно трёхмерной молекулярный ион водорода[6][7]. В этом случае правая сторона уравнения (1) (или (2)) теперь становится отношением двух беспредельных многочленов по переменной x:
- где ri и si константы, а x является функцией между внутренней энергией и расстоянием внутри ядра R. Уравнение (3), а также его упрощённые формы, выраженные в уравнениях (1) и (2), относятся к типу дифференциальных уравнений с запозданием.
Применения W-функции Ламберта в основных проблемах физики не ограничиваются стандартным уравнением (1), как было недавно показано в областях атомной, молекулярной и оптической физики[8] и критерий «Кейпер-Ли» для Гипотеза Римана[9].
Вычисление
[править | править код]-функция может быть приблизительно вычислена с помощью рекуррентного соотношения[1]:
Пример программы на языке Python:
import math
def lambertW(x, prec=1e-12):
w = 0
for i in range(100):
wTimesExpW = w * math.exp(w)
wPlusOneTimesExpW = (w + 1) * math.exp(w)
w -= (wTimesExpW - x) / (wPlusOneTimesExpW - (w + 2) * (wTimesExpW - x) / (2 * w + 2))
if prec > abs((x - wTimesExpW) / wPlusOneTimesExpW):
break
if prec <= abs((x - wTimesExpW) / wPlusOneTimesExpW):
raise Exception("W(x) не сходится достаточно быстро при x=%f" % x)
return w
Для приближённого вычисления можно использовать следующую формулу[10]. Приведённая функция похожа, но более чем на 10 % отличается от функции Ламберта.
Примечания
[править | править код]- ↑ 1 2 Corless et al. On the Lambert W function (неопр.) // Adv. Computational Maths.. — 1996. — Т. 5. — С. 329—359. Архивировано 18 января 2005 года.
- ↑ T. C. Scott, R. B. Mann. General Relativity and Quantum Mechanics: Towards a Generalization of the Lambert W Function (англ.) // AAECC (Applicable Algebra in Engineering, Communication and Computing) : journal. — 2006. — Vol. 17, no. 1. — P. 41—47. — doi:10.1007/s00200-006-0196-1. Архивировано 11 июня 2019 года.
- ↑ T. C. Scott, G. Fee, J. Grotendorst. Asymptotic series of Generalized Lambert W Function (англ.) // SIGSAM (ACM Special Interest Group in Symbolic and Algebraic Manipulation) : journal. — 2013. — Vol. 47, no. 185. — P. 75—83. Архивировано 14 июля 2014 года.
- ↑ T. C. Scott, G. Fee, J. Grotendorst, W.Z. Zhang. Numerics of the Generalized Lambert W Function (неопр.) // SIGSAM. — 2014. — Т. 48, № 1/2. — С. 42—56. Архивировано 14 июля 2014 года.
- ↑ P. S. Farrugia, R. B. Mann, T. C. Scott. N-body Gravity and the Schrödinger Equation (англ.) // Classical and Quantum Gravity : journal. — 2007. — Vol. 24, no. 18. — P. 4647—4659. — doi:10.1088/0264-9381/24/18/006. Архивировано 6 апреля 2019 года.
- ↑ T. C. Scott, M. Aubert-Frécon, J. Grotendorst. New Approach for the Electronic Energies of the Hydrogen Molecular Ion (англ.) // Chem. Phys.[англ.] : journal. — 2006. — Vol. 324. — P. 323—338. — doi:10.1016/j.chemphys.2005.10.031. Архивировано 18 января 2016 года.
- ↑ Maignan, Aude; Scott, T. C. Fleshing out the Generalized Lambert W Function (неопр.) // SIGSAM. — 2016. — Т. 50, № 2. — С. 45—60. — doi:10.1145/2992274.2992275.
- ↑ T. C. Scott, A. Lüchow, D. Bressanini, J. D. Morgan III. The Nodal Surfaces of Helium Atom Eigenfunctions (англ.) // Phys. Rev. A : journal. — 2007. — Vol. 75. — P. 060101. — doi:10.1103/PhysRevA.75.060101.
- ↑ R.C. McPhedran; T. C. Scott; Aude Maignan. The Keiper-Li Criterion for the Riemann Hypothesis and Generalized Lambert Functions (неопр.) // ACM Commun. Comput. Algebra. — 2016. — Т. 57, № 3. — С. 85-110. — doi:10.1145/3637529.3637530.
- ↑ Double precision function LAMBERTW(X) Архивная копия от 2 сентября 2005 на Wayback Machine в пакете QCDINS Архивная копия от 4 апреля 2005 на Wayback Machine






























































