Метод коллинеарных градиентов: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
| (не показано 5 промежуточных версий этого же участника) | |||
| Строка 4: | Строка 4: | ||
=== Идея метода === |
=== Идея метода === |
||
Для гладкой функции <math>J(u)</math> в относительно большой окрестности точки <math>u^k</math> |
Для гладкой функции <math>J(u)</math> в относительно большой окрестности точки <math>u^k</math> найдётся точка <math>u^{k_\ast}</math>, где градиенты <math>\nabla J^k\,\overset{\textrm{def}}{=}\,\nabla J(u^k)</math> и <math>\nabla J^{k_\ast}\,\overset{\textrm{def}}{=}\,\nabla J(u^{k_\ast})</math> коллинеарные. Направлением на экстремум <math>u_\ast</math> из точки <math>u^k</math> будет направление <math>d^k={(u^{k_\ast}-u}^k)</math>. Вектор <math>d^k</math> указывает на максимум или на минимум в зависимости от положения точки <math>u^{k_\ast}</math>. Она может быть спереди или сзади от <math>u^k</math> относительно направления на <math>u_\ast</math> (см. рисунок). Далее будем рассматривать минимизацию. |
||
Очередная |
Очередная {{font color|pink||итерация МКГ}}: |
||
(1) <math>\quad u^{k+1}=u^k+b^kd^k, \quad k |
(1) <math>\quad u^{k+1}=u^k+b^kd^k, \quad k\in \left\{ 0,1\dots\right\},</math> |
||
где оптимальное <math>b^k\in \mathbb R</math> находится аналитически из предположения [[Квадратичная функция одной переменной|квадратичности одномерной функции]] <math>J(u^k+bd^k)</math>: |
где оптимальное <math>b^k\in \mathbb R</math> находится аналитически из предположения [[Квадратичная функция одной переменной|квадратичности одномерной функции]] <math>J(u^k+bd^k)</math>: |
||
| Строка 15: | Строка 15: | ||
Угловые скобки — это [[скалярное произведение]] в [[Евклидово пространство|евклидовом пространстве]] <math>\mathbb R^n</math>. Если <math>J(u)</math> [[выпуклая функция]] в окрестности <math>u^k</math>, то для передней точки <math>u^{k_\ast}</math> получаем число <math>b^k>0</math>, для задней <math>b^k<0</math>. Делаем шаг (1). |
Угловые скобки — это [[скалярное произведение]] в [[Евклидово пространство|евклидовом пространстве]] <math>\mathbb R^n</math>. Если <math>J(u)</math> [[выпуклая функция]] в окрестности <math>u^k</math>, то для передней точки <math>u^{k_\ast}</math> получаем число <math>b^k>0</math>, для задней <math>b^k<0</math>. Делаем шаг (1). |
||
Для строго выпуклой квадратичной функции <math>J(u)</math> |
Для строго выпуклой квадратичной функции <math>J(u)</math> {{font color|pink||шаг МКГ}} |
||
<math>b^kd^k=-H^{-1}\nabla J^k,</math> |
<math>b^kd^k=-H^{-1}\nabla J^k,</math> |
||
т.е. это |
т.е. {{font color|pink||это шаг [[метод Ньютона|метода Ньютона]]}} (метод второго порядка с квадратичной скоростью сходимости), где <math>H</math> — [[матрица Гессе]]. Такие шаги обеспечивают МКГ квадратичную скорость сходимости. |
||
В общем случае, если <math>J(u)</math> имеет переменную выпуклость и возможны [[Седловая точка|седловые точки]], то следует контролировать направление минимизации по углу <math>\gamma</math> между векторами <math>\nabla J^k</math> и <math>d^k</math>. Если <math>\cos(\gamma)=\frac{\langle \nabla J^k,d^k\rangle}{||\nabla J(u^k)||\; ||d^k||}\geq 0</math>, то <math>d^k</math> — это направление максимизации и в (1) следует брать <math>b^k</math> с обратным знаком. |
В общем случае, если <math>J(u)</math> имеет переменную выпуклость и возможны [[Седловая точка|седловые точки]], то следует контролировать направление минимизации по углу <math>\gamma</math> между векторами <math>\nabla J^k</math> и <math>d^k</math>. Если <math>\cos(\gamma)=\frac{\langle \nabla J^k,d^k\rangle}{||\nabla J(u^k)||\; ||d^k||}\geq 0</math>, то <math>d^k</math> — это направление максимизации и в (1) следует брать <math>b^k</math> с обратным знаком. |
||
== Поиск коллинеарных градиентов == |
|||
{{font color|pink||Коллинеарность градиентов}} оценивается [[невязка|невязкой]] их [[орт вектора|ортов]], которая имеет вид системы <math>n</math> уравнений для поиска корня <math>u=u^{k_\ast}</math>: |
|||
(3) <math>\quad r^k(u)=\frac{\nabla J(u)}{||\nabla J(u)||}s-\frac{\nabla J(u^k)}{||\nabla J(u^k)||}=0 \in \mathbb R^n,</math> |
(3) <math>\quad r^k(u)=\frac{\nabla J(u)}{||\nabla J(u)||}s-\frac{\nabla J(u^k)}{||\nabla J(u^k)||}=0 \in \mathbb R^n,</math> |
||
где [[sgn|знак]] <math>s=\sgn\langle\nabla J(u),\nabla J(u^k)\rangle</math> позволяет одинаково оценивать коллинеарность градиентов по одну или разные стороны от минимума <math>u_\ast</math>, <math>||r^k(u)||\le \sqrt{2}</math>. |
где [[sgn|знак]] <math>s=\sgn\langle\nabla J(u),\nabla J(u^k)\rangle</math> позволяет одинаково оценивать коллинеарность градиентов по одну или разные стороны от минимума <math>u_\ast</math>, <math>||r^k(u)||\le \sqrt{2}</math>. |
||
| Строка 32: | Строка 32: | ||
: (4) <math>\quad u^{k_{l+1}}=u^{k_l}+\tau^lp^l, \quad l=1,2\ldots,</math> |
: (4) <math>\quad u^{k_{l+1}}=u^{k_l}+\tau^lp^l, \quad l=1,2\ldots,</math> |
||
где вектор <math>p^l\ |
где вектор <math>\;p^l\;\overset{\textrm{def}}{=}\,p(u^{k_l})=-r^l+{\beta^lp}^{l-1}</math>, <math>\;r^l\,\overset{\textrm{def}}{=}\,r(u^{k_l})</math>, <math>\;\beta^l=||r^l||^2/||r^{l-1}||^2, \ \beta^{1,n,2n...}=0</math>, <math>\;\tau^l=||r^l||^2/\langle p^l,H^lp^l\rangle</math>, произведение матрицы Гессе <math>H^l</math> на <math>p^l</math> находится численным дифференцированием: |
||
: (5) <math>\quad H^lp^l\approx \frac{r(u^{k_h})-r(u^{k_l})}{h/||p^l||},</math> |
: (5) <math>\quad H^lp^l\approx \frac{r(u^{k_h})-r(u^{k_l})}{h/||p^l||},</math> |
||
| Строка 57: | Строка 57: | ||
== Алгоритм выбора направления минимизации == |
== Алгоритм выбора направления минимизации == |
||
* Параметры: <math>c_1, c_2, \delta^0, \delta_m = 10^{-15}\delta^0, h=10^{-5}</math>. |
|||
* |
* <code>Параметры: <math>c_1, c_2, \delta^0, \delta_m = 10^{-15}\delta^0, h=10^{-5}</math>.</code> |
||
* <code>Входные данные: <math>n, k=0, u^k, J(u^k), \nabla J(u^k), \nabla J^k </math>.</code> |
|||
# |
# <code><math>l=1</math>. Если <math>k>0</math> задаём <math>\delta^k</math> из (7).</code> |
||
# Вычисляем <math>\nabla J^l, ||\nabla J^l||</math> и находим <math>r^l</math> из (3) при <math>u=u^{k_l}</math>. |
# <code>Находим <math>u^{k_l}</math> из (6).</code> |
||
# <code>Вычисляем <math>\nabla J^l, ||\nabla J^l||</math> и находим <math>r^l</math> из (3) при <math>u=u^{k_l}</math>.</code> |
|||
# Если <math>||r^l||\leq c_1\sqrt{2}\,</math> или <math> l \geq l_{max}</math>, или <math>||u^{k_l}-u^k|| < \delta_m </math>, или {<math>\,l>1</math> и <math>\left| \frac{||r^l||-||r^{l-1}||}{||r^l||}\right| \leq c_1 </math>}, то принимаем <math>u^{k_\ast}=u^{k_l}</math>, возвращаем <math>\nabla J\left(u^{k_\ast}\right)</math>, <math>d^k={(u^{k_\ast}-u}^k)</math>, '''<big>стоп</big>''' |
# <code>Если <math>||r^l||\leq c_1\sqrt{2}\,</math> или <math> l \geq l_{max}</math>, или <math>||u^{k_l}-u^k|| < \delta_m </math>, или {<math>\,l>1</math> и <math>\left| \frac{||r^l||-||r^{l-1}||}{||r^l||}\right| \leq c_1 </math>}, то принимаем <math>u^{k_\ast}=u^{k_l}</math>, возвращаем <math>\nabla J\left(u^{k_\ast}\right)</math>, <math>d^k={(u^{k_\ast}-u}^k)</math>, {{font color||red|'''<big>стоп</big>'''}}.</code> |
||
# Если <math>l\neq 1,n,2n,3n\ldots</math>, задаём <math>\beta^l=||r^l||^2/||r^{l-1}||^2</math>, иначе <math>\beta^l=0</math>. |
# <code>Если <math>l\neq 1,n,2n,3n\ldots</math>, задаём <math>\beta^l=||r^l||^2/||r^{l-1}||^2</math>, иначе <math>\beta^l=0</math>.</code> |
||
# Вычисляем <math>p^l=-r^l+\beta^l p^{l-1}</math>. |
# <code>Вычисляем <math>p^l=-r^l+\beta^l p^{l-1}</math>.</code> |
||
# Находим шаговый множитель <math>\tau^l</math> для подитераций: |
# <code>Находим шаговый множитель <math>\tau^l</math> для подитераций:</code> |
||
## запоминаем <math>u^{k_l}</math>, <math>\nabla J^l</math>, <math>||\nabla J^l||</math>, <math>r^l</math>, <math>||r^l||</math>; |
## <code>запоминаем <math>u^{k_l}</math>, <math>\nabla J^l</math>, <math>||\nabla J^l||</math>, <math>r^l</math>, <math>||r^l||</math>;</code> |
||
## задаём <math>u^{k_h}=u^{k_l}+hp^l/||p^l||</math>, вычисляем <math>\nabla J(u^{k_h})</math>, <math>r\left(u^{k_h}\right)</math> и находим <math>H^lp^l</math> из (5), присваиваем <math>w\leftarrow\langle p^l,H^lp^l\rangle</math>; |
## <code>задаём <math>u^{k_h}=u^{k_l}+hp^l/||p^l||</math>, вычисляем <math>\nabla J(u^{k_h})</math>, <math>r\left(u^{k_h}\right)</math> и находим <math>H^lp^l</math> из (5), присваиваем <math>w\leftarrow\langle p^l,H^lp^l\rangle</math>;</code> |
||
## если <math>w=0</math>, тогда <math>h\leftarrow 10h</math>, возвращаемся к шагу 7.2; |
## <code>если <math>w=0</math>, тогда <math>h\leftarrow 10h</math>, возвращаемся к шагу 7.2;</code> |
||
## восстанавливаем <math>u^{k_l}</math>, <math>\nabla J^l</math>, <math>||\nabla J^l||</math>, <math>r^l</math>, <math>||r^l||</math>; |
## <code>восстанавливаем <math>u^{k_l}</math>, <math>\nabla J^l</math>, <math>||\nabla J^l||</math>, <math>r^l</math>, <math>||r^l||</math>;</code> |
||
## находим <math>\tau^l=||r^l||^2/w </math>. |
## <code>находим <math>\tau^l=||r^l||^2/w </math>.</code> |
||
# Делаем подитерацию <math>u^{k_{l+1}}</math> из (4). |
# <code>Делаем подитерацию <math>u^{k_{l+1}}</math> из (4).</code> |
||
# <math>l\leftarrow l+1</math>, переходим к шагу 3. |
# <code><math>l\leftarrow l+1</math>, переходим к шагу 3.</code> |
||
Параметр <math>c_2=3\div 5</math>. Для функций без седловых точек рекомендуется <math>c_1\approx 10^{-8}</math>, <math>\delta\approx{10}^{-5}</math>. Для «обхода» седловых точек рекомендуется <math>c_1\approx 0.1</math>, <math>\delta\approx 0.1</math>. |
Параметр <math>c_2=3\div 5</math>. Для функций без седловых точек рекомендуется <math>c_1\approx 10^{-8}</math>, <math>\delta\approx{10}^{-5}</math>. Для «обхода» седловых точек рекомендуется <math>c_1\approx 0.1</math>, <math>\delta\approx 0.1</math>. |
||
Описанный алгоритм позволяет приблизительно найти коллинеарные градиенты из системы уравнений (3). |
Описанный алгоритм позволяет приблизительно найти коллинеарные градиенты из системы уравнений (3). Полученное направление <math>b^kd^k</math> для алгоритма МКГ (1) будет {{font color|pink||приблизительным направлением Ньютона}} (truncated Newton method). |
||
== Демонстрации<ref>''Tolstykh V.K.'' Демонстрационное Windows-приложение [https://tolstykh.com/docs/Оптимизация/optimization.rar Optimization ]</ref> == |
== Демонстрации<ref>''Tolstykh V.K.'' Демонстрационное Windows-приложение [https://tolstykh.com/docs/Оптимизация/optimization.rar Optimization ]</ref> == |
||
| Строка 95: | Строка 96: | ||
С ростом размерности <math>\color{red}n</math>, вычислительные погрешности при реализации условия коллинеарности (3), могут заметно возрастать. Поэтому МКГ, по сравнению с методом Ньютона, в рассматриваемом примере потребовал более одной итерации. |
|||
[[Файл:ColGM-Rosenbrock.png|thumb|Минимизация МКГ: 3 итерации и 16 вычислений <math>J</math> и <math>\nabla J</math>]] |
[[Файл:ColGM-Rosenbrock.png|thumb|Минимизация МКГ: 3 итерации и 16 вычислений <math>J</math> и <math>\nabla J</math>]] |
||
| Строка 120: | Строка 121: | ||
МКГ является очень экономичным по количеству вычислений <math>J</math> и <math>\nabla J</math>. Благодаря формуле (2), он не требует затратных вычислений шагового множителя <math>b^k</math> посредством линейного поиска |
{{font color|pink||МКГ является очень экономичным}} по количеству вычислений <math>J</math> и <math>\nabla J</math>. Благодаря формуле (2), он не требует затратных вычислений шагового множителя <math>b^k</math> посредством линейного поиска (например, [[метод золотого сечения|методом золотого сечения]] и т.п.). |
||
== Примечания == |
== Примечания == |
||
{{примечания}} |
{{примечания}} |
||
Версия от 15:11, 27 декабря 2024
Метод коллинеарных градиентов (МКГ)[1] — итерационный метод направленного поиска локального экстремума гладкой функции многих переменных с движением к экстремуму вдоль вектора такого, где градиенты и коллинеарные. Это метод перового порядка (использует только первые производные ) с квадратичной скоростью сходимости. Может применяться к функциям высокой размерности с несколькими локальными экстремумами. МКГ можно отнести к семейству методов Truncated Newton method

Идея метода
Для гладкой функции в относительно большой окрестности точки найдётся точка , где градиенты и коллинеарные. Направлением на экстремум из точки будет направление . Вектор указывает на максимум или на минимум в зависимости от положения точки . Она может быть спереди или сзади от относительно направления на (см. рисунок). Далее будем рассматривать минимизацию.
Очередная итерация МКГ:
(1)
где оптимальное находится аналитически из предположения квадратичности одномерной функции :
- (2)
Угловые скобки — это скалярное произведение в евклидовом пространстве . Если выпуклая функция в окрестности , то для передней точки получаем число , для задней . Делаем шаг (1).
Для строго выпуклой квадратичной функции шаг МКГ
т.е. это шаг метода Ньютона (метод второго порядка с квадратичной скоростью сходимости), где — матрица Гессе. Такие шаги обеспечивают МКГ квадратичную скорость сходимости.
В общем случае, если имеет переменную выпуклость и возможны седловые точки, то следует контролировать направление минимизации по углу между векторами и . Если , то — это направление максимизации и в (1) следует брать с обратным знаком.
Поиск коллинеарных градиентов
Коллинеарность градиентов оценивается невязкой их ортов, которая имеет вид системы уравнений для поиска корня :
(3)
где знак позволяет одинаково оценивать коллинеарность градиентов по одну или разные стороны от минимума , .
Система (3) решается итерационно (подитерации ) методом сопряжённых градиентов в предположении, что она линейна в окрестности :
- (4)
где вектор , , , , произведение матрицы Гессе на находится численным дифференцированием:
- (5)
где , — малое положительное число такое, что .
Начальное приближение задаётся под 45° ко всем осям координат длинной :
- (6)
Начальный радиус -окрестности точки корректируется:
- (7)
Необходимо . Здесь малое положительное число заметно больше машинного эпсилон.
Подитерации завершаются при выполнении хотя бы одного из условий:
- — достигнута точность;
- — прекратилась сходимость;
- — избыточность подитераций.
Алгоритм выбора направления минимизации
Параметры: .Входные данные: .
. Если задаём из (7).Находим из (6).Вычисляем и находим из (3) при .Если или , или , или { и }, то принимаем , возвращаем , , стоп.Если , задаём , иначе .Вычисляем .Находим шаговый множитель для подитераций:запоминаем , , , , ;задаём , вычисляем , и находим из (5), присваиваем ;если , тогда , возвращаемся к шагу 7.2;восстанавливаем , , , , ;находим .
Делаем подитерацию из (4)., переходим к шагу 3.
Параметр . Для функций без седловых точек рекомендуется , . Для «обхода» седловых точек рекомендуется , .
Описанный алгоритм позволяет приблизительно найти коллинеарные градиенты из системы уравнений (3). Полученное направление для алгоритма МКГ (1) будет приблизительным направлением Ньютона (truncated Newton method).
Демонстрации[2]
Во всех демонстрациях МКГ показывает сходимость не хуже, а иногда и лучше (для функций переменной выпуклости), чем метод Ньютона.
Тестовая функция «повёрнутый эллипсоид»
Строго выпуклая квадратичная функция:
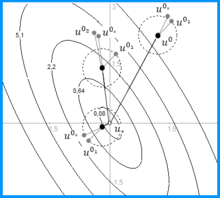
На рисунке для заданы три чёрные стартовые точки . Серые точки — подитерации с (показано пунктиром, завышено для демонстрации). Параметры , . Для всех потребовалась одна итерация и подитераций не более двух.
При (параметр ) с начальной точкой МКГ достиг с точностью 1 % за 3 итерации и 754 вычисления и . Другие методы первого порядка: Квазиньютоновский BFGS (работа с матрицами) потребовал 66 итераций и 788 вычислений; сопряжённых градиентов (Fletcher-Reeves) — 274 итерации и 2236 вычислений; конечно-разностный метод Ньютона — 1 итерация и 1001 вычислений. Метод Ньютона второго порядка — 1 итерация.
С ростом размерности , вычислительные погрешности при реализации условия коллинеарности (3), могут заметно возрастать. Поэтому МКГ, по сравнению с методом Ньютона, в рассматриваемом примере потребовал более одной итерации.

Тестовая функция Розенброка
Параметры те же, кроме . Траектория спуска МКГ полностью совпадает с методом Ньютона. На рисунке синяя начальная точка , красная — . В каждой точке нарисованы орты градиентов.
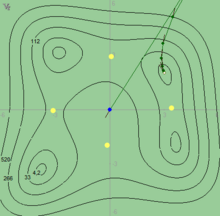
Тестовая функция Химмельблау
Параметры , .
 |
 |
 |
 |
МКГ является очень экономичным по количеству вычислений и . Благодаря формуле (2), он не требует затратных вычислений шагового множителя посредством линейного поиска (например, методом золотого сечения и т.п.).
Примечания
- ↑ Tolstykh V.K. Collinear Gradients Method for Minimizing Smooth Functions // Oper. Res. Forum. — 2023. — Vol. 4. — No. 20. — doi: s43069-023-00193-9
- ↑ Tolstykh V.K. Демонстрационное Windows-приложение Optimization
















































![{\displaystyle \quad \delta ^{k}=\max \left[\min \left(\delta ^{k-1}{\frac {||\nabla J(u^{k})||}{||\nabla J(u^{k-1})||}},\delta ^{0}\right),\delta _{m}\right],\quad k>0.}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/84ad5d9059083cfb166dd50014aaec89daf4d3ea)






























































