Кратный интеграл

Кратный интеграл — определённый интеграл, взятый от $n>1$ переменных; например:

$\underbrace {\int \cdots \int } _{n}f(x_{1},\ldots ,x_{n})dx_{1}\cdots dx_{n}$.

В классическом анализе чаще всего используются двойной интеграл и тройной интеграл — интегралы от двух и трёх переменных соответственно.

Определение

В общем случае кратный интеграл определяется для функции $f\colon B\to \mathbb {R}$ на жорданово измеримом множестве $B\subset \mathbb {R} ^{n}$ с использованием понятия разбиения $\sigma$ — набора попарно непересекающихся подмножеств $\sigma =\left\{{{U}_{i}}\subset B\right\}$, которые в объединение дают всё $B$. Мелкостью $\left|\sigma \right|$ измерения называется наибольший диаметр множеств $U_{i}\in \sigma$:

$\left|\sigma \right|=\max \left\{\operatorname {diam} \left({{U}_{i}}\right)\right\}$.

Разбиение называется конечным, если является конечным множеством, и измеримым, если все его элементы — измеримые (в данном случае — по Жордану) множества.

Кратным ($n$-кратным) интегралом функции $f$ на $B$ называется число $I$ (если оно существует), такое, что при любой $\varepsilon$-окрестности числа $I$ всегда найдётся такое разбиение множества $B$ и набор промежуточных точек, что сумма произведений значения функции в промежуточной точке разбиения на меру разбиения будет попадать в эту окрестность:

$\forall \varepsilon >0\;\;\exists \delta >0$ : $\sigma =\{U_{i}\}_{i=1}^{m}$ : $\left|\sigma \right|<\delta \;\forall \xi _{i}\in U_{i}\;\;\left|{\sum _{i=1}^{m}f(\xi _{i})\mu (U_{i})-I}\right|<\varepsilon$.

(здесь $\mu (U_{i})$ — мера множества $U_{i}$.

Это определение можно сформулировать в другой форме с использованием интегральных сумм: для данного разбиения $\sigma =\{U_{i}\}_{i=1}^{m}$ и множества точек $\xi =\{\xi _{i}\in U_{i}\}$ рассматривается интегральная сумма:

$\zeta (f,\sigma ,\xi )=\sum _{i=1}^{m}f(\xi _{i})\mu (U_{i})$,

тогда кратным интегралом функции $f\colon B\to \mathbb {R}$ называют предел:

$I=\lim _{\left|\sigma \right|\to 0}\zeta (f,\sigma ,\xi )$,

если он существует. Предел берётся по множеству всех последовательностей разбиений, с мелкостью стремящейся к 0. Разумеется, это определение отличается от предыдущего, по сути, лишь используемым языком.

В случае $n=1$ кратный интеграл совпадает с интегралом Римана.

Обозначение

В современном анализе чаще всего используется векторная форма записи:

$\int \limits _{G}{f\left(X\right)dX}=I$.

Иногда ставят знак интеграла $n$ раз, записывают функцию и $n$ дифференциалов:

$\underbrace {\int {\cdots }\int } _{n}f({x_{1}},\ldots ,{x_{n}})d{x_{1}}\cdots d{x_{n}}=I$.

Для двойного и тройного интегралов используются также обозначения $\iint$ и $\iiint$ соответственно.

Многократное использование знака характерно для учебной литературы, в современных научных работах используется редко.

Существование кратного интеграла

Если функция непрерывна на измеримом по Жордану компакте, то она интегрируема на нем. Как следствие, неограниченная функция на множестве может быть не интегрируемой, даже если она непрерывна. Например, функция $y=1/x$ не интегрируема на интервале $\left(0;1\right)$.

Если функция определена на измеримом по Жордану множестве, у которого существуют сколь угодно мелкие разбиения, для которых данная функция неограничена на объединении всех их элементов положительной меры, то эта функция неинтегрируема на этом множестве.

Критерий Дарбу: если существуют верхний $I^{*}$ и нижний $I_{*}$ интегралы Дарбу функции на $G$, тогда, если верхний и нижний интегралы Дарбу равны, то данная функция интегрируема на $G$, причём:

$I^{*}=I_{*}=\int \limits _{G}{f\left(X\right)dX}$.

Критерий Лебега: если $G$ — измеримое по Жордану множество, то $f$ интегрируема на $G$ если она ограничена на $G$ и непрерывна на $G\setminus E$, где множество $E$ имеет меру Лебега нуль.

Свойства кратных интегралов

Кратные интегралы линейны по функции: если $G$ измеримо, функции $f$ и $g$ интегрируемы на $G$, то:

$\forall \lambda ,\mu \in \mathbb {R} :~\int \limits _{G}{\left(\lambda f+\mu g\right)dX}=\lambda \int \limits _{G}{fdX}+\mu \int \limits _{G}{gdX}$.

Аддитивность по множеству интегрирования позволяет раздельно проинтегрировать по частям областей: если ${G}_{1}$ и $G_{2}$ измеримы, $G_{1}\cap G_{2}=\varnothing$ и $G_{1}\cup G_{2}=G$, а функция $f(X)$ определена и интегрируема на каждом из множеств $G_{1}$ и $G_{2}$, то интеграл по $G$ существует и равен сумме интегралов по $G_{1}$ и $G_{2}$:

$\int _{G}f(X)dX=\int _{G_{1}}f(X)dX+\int _{G_{2}}f(X)dX$.

Кратные интегралы монотонны по функции: если $G$ измеримо, функции $f$ и $g$ интегрируемы на $G$, причём $\forall X\in G\colon f\left(X\right)\leqslant g\left(X\right)$, то:

$\int _{G}f(X)dX\leqslant \int _{G}g(X)dX$.

Интегральное неравенство треугольника (следствие монотонности):

$\left|\int _{G}f(X)dX\right|\leqslant \int _{G}\left|f(X)\right|dX$

Интегральная теорема о среднем: если $G$ — компакт, функция $f(X)$ непрерывна и интегрируема на $G$, тогда:

$\exists Y\in G\colon \int _{G}f(X)dX=f(Y)\mu (G)$.

Постоянная функция $f(X)=c$ интегрируема на любом измеримом множестве $G$, причём:

$\int _{G}f(X)dX=c\cdot \mu (G)$.

Как следствие, $\ \int _{G}dX=\mu (G)$.

Вычисление кратных интегралов

Сведение кратного интеграла к повторным

Пусть $D\subset {{\mathbb {R} }^{d-1}}$ — измеримое множество, $G=\left\{\left({{x}_{1}},\ldots ,{{x}_{n}}\right):\left({{x}_{1}},\ldots ,{{x}_{n-1}}\right)\in D;\varphi \left({{x}_{1}},\ldots ,{{x}_{n-1}}\right)\leq {{x}_{n}}\leq \psi \left({{x}_{1}},\ldots ,{{x}_{n-1}}\right)\right\}$ — также измеримое множество, $f\left(X\right)$ определена и интегрируема на $\ G$. Тогда

• $\int \limits _{\ \varphi \left({{x}_{1}},\ldots ,{{x}_{n-1}}\right)}^{\psi \left({{x}_{1}},\ldots ,{{x}_{n-1}}\right)}{f\left({{x}_{1}},\ldots ,{{x}_{n}}\right)d{{x}_{n}}}\equiv I\left({{x}_{1}},\ldots ,{{x}_{n-1}}\right)$ существует всюду на $D$, кроме множества $D_{0}$ Лебеговой меры нуль ($D_{0}$ может быть пустым);
• существует $\int \limits _{D}{\tilde {I}}\left({{x}_{1}},\ldots ,{{x}_{n-1}}\right)d{{x}_{1}}\ldots d{{x}_{n-1}}\equiv \int \limits _{D}{\left[\int \limits _{\,\varphi \left({{x}_{1}},\ldots ,{{x}_{n-1}}\right)}^{\psi \left({{x}_{1}},\ldots ,{{x}_{n-1}}\right)}{f\left({{x}_{1}},\ldots ,{{x}_{n}}\right)d{{x}_{n}}}\right]d{{x}_{1}}\ldots d{{x}_{n-1}}}$, где

${\tilde {I}}\left({{x}_{1}},\ldots ,{{x}_{n-1}}\right)\equiv {\begin{cases}I\left({{x}_{1}},\ldots ,{{x}_{n-1}}\right),&({{x}_{1}},\ldots ,{{x}_{n-1}})\in D\backslash D_{0}\\\qquad \quad 0&({{x}_{1}},\ldots ,{{x}_{n-1}})\in D_{0},\end{cases}}$

называемый повторным интегралом от функции $f\left({{x}_{1}},\ldots ,{{x}_{n-1}}\right)$ по множеству $G$;

• $\int \limits _{G}{f\left({{x}_{1}},\ldots ,{{x}_{n}}\right)d{{x}_{1}}\ldots d{{x}_{n}}}=\int \limits _{D}{\left[\int \limits _{\,\varphi \left({{x}_{1}},\ldots ,{{x}_{n-1}}\right)}^{\psi \left({{x}_{1}},\ldots ,{{x}_{n-1}}\right)}{f\left({{x}_{1}},\ldots ,{{x}_{n}}\right)d{{x}_{n}}}\right]d{{x}_{1}}\ldots d{{x}_{n-1}}}$.

Любой $n$-мерный интеграл можно свести к $n$ одномерным.

Замена переменных

Пусть задано биективное отображение ${{\mathbb {R} }^{d}}\leftrightarrow {{\mathbb {R} }^{d}}$, переводящее область $\ {{D}'}$ в $\ D$:

$\left\{{\begin{aligned}{{t}_{1}}={{\psi }_{1}}\left({{x}_{1}},\ldots ,{{x}_{n}}\right)\\{{t}_{2}}={{\psi }_{2}}\left({{x}_{1}},\ldots ,{{x}_{n}}\right)\\\ldots \\{{t}_{n}}={{\psi }_{n}}\left({{x}_{1}},\ldots ,{{x}_{n}}\right)\\\end{aligned}}\right.$,

где $t$ — «старые» координаты, а $x$ — «новые» координаты. Пусть далее функции, задающие отображение, имеют в области $\ {{D}'}$ непрерывные частные производные первого порядка, а также ограниченный и отличный от нуля якобиан

${\frac {D\left(t\right)}{D\left(x\right)}}={\frac {D\left({{t}_{1}},\ldots ,{{t}_{n}}\right)}{D\left({{x}_{1}},\ldots ,{{x}_{n}}\right)}}$.

Тогда при условии существования интеграла

$\int \limits _{D}{f\left(T\right)dT}=\int {\int \limits _{D}{\ldots \int {f\left({{t}_{1}},\ldots ,{{t}_{n}}\right)d{{t}_{1}}\ldots d{{t}_{n}}}}}$

справедлива формула замены переменных:

$\int {\int \limits _{D}{\ldots \int {f\left({{t}_{1}},\ldots ,{{t}_{n}}\right)d{{t}_{1}}\ldots d{{t}_{n}}}}}=\int {\int \limits _{{D}'}{\ldots \int {f\left({{\psi }_{1}}\left({{x}_{1}},\ldots ,{{x}_{n}}\right),\ldots ,{{\psi }_{n}}\left({{x}_{1}},\ldots ,{{x}_{n}}\right)\right)\left|{\frac {D\left({{t}_{1}},\ldots ,{{t}_{n}}\right)}{D\left({{x}_{1}},\ldots ,{{x}_{n}}\right)}}\right|d{{x}_{1}}\ldots d{{x}_{n}}}}}$

Использование симметрии

Если область интегрирования симметрична относительно начала координат по крайней мере для одной из переменных интегрирования и подынтегральная функция нечётна по этой переменной, интеграл равен нулю, поскольку интегралы по двум половинкам области интегрирования имеют одно и то же абсолютное значение, но противоположные знаки. Если подынтегральная функция чётна по этой переменной, интеграл равен удвоенному интегралу по одной из половинок области интегрирования, поскольку интегралы по каждой из половинок равны.

Например, если функция $f(x,y)=2\sin(x)-3y^{3}+5$ интегрируется по области:

$T=\left\{(x,y)\in \mathbf {R} ^{2}\ :\ x^{2}+y^{2}\leq 1\right\}$ —

кругу радиуса 1 с центром в начале координат, то используя свойство линейности, интеграл можно разложить на три части:

$\iint _{T}(2\sin x-3y^{3}+5)\,dx\,dy=\iint _{T}2\sin x\,dx\,dy-\iint _{T}3y^{3}\,dx\,dy+\iint _{T}5\,dx\,dy$

$2\sin x$ и $3y^{3}$ являются нечётными функциями и, кроме того, очевидно, что диск $T$ симметричен как относительно оси $x$, так и по оси $y$. Таким образом, вклад в конечный результат даёт только константа 5.

В примере для интегрирования функции $f(x,y,z)=x\exp(y^{2}+z^{2})$ по сфере радиуса 2 с центром в начале координат:

$T=\left\{(x,y,z)\in \mathbb {R} ^{3}\ :\ x^{2}+y^{2}+z^{2}\leq 4\right\}$

достаточно проинтегрировать по оси $x$, чтобы показать, что интеграл равен 0, поскольку по этой переменной функция нечётна.

Двойной интеграл

Геометрический смысл двойного интеграла

Двойным интегралом называют кратный интеграл с $n=2$:

$\iint \limits _{D}{f\left(P\right)d\sigma }$.

Здесь $\ d\sigma$ — элемент площади в рассматриваемых координатах.

В прямоугольных координатах: $\iint \limits _{D}{f\left(x,y\right)dxdy}$, где $\ dxdy$ — элемент площади в прямоугольных координатах.

Геометрический смысл

Пусть функция $f\left(x,y\right)$ принимает в области $D$ только положительные значения. Тогда двойной интеграл $\iint \limits _{D}{f\left(x,y\right)d\sigma }::$ численно равен объёму $\ V$ вертикального цилиндрического тела, построенного на основании $\ D$ и ограниченного сверху соответствующим куском поверхности $z=f\left(x,y\right)$.

Выражение через полярные координаты

Переход из прямоугольных координат в полярные.

Переход из прямоугольных координат в полярные.

В некоторых случаях двойной интеграл проще считать не в прямоугольных, а в полярных координатах, так как при этом может произойти существенное упрощение вида области интегрирования и всего процесса интегрирования в целом.

Для выражения через полярные координаты используется следующая замена переменных:

$x=r\cos \varphi$, $y=r\sin \varphi$.

Модуль якобиана отображения равен $r$. Таким образом:

$\iint \limits _{D}{f\left(x,y\right)dxdy}=\iint \limits _{{D}'}{g\left(r,\varphi \right)rdrd\varphi },\quad$ где $g\left(r,\varphi \right)=f\left(r\cos \varphi ,r\sin \varphi \right)$.

Здесь $rdrd\varphi$ является элементом площади в полярных координатах.

Приложения двойных интегралов

Наименование величины	Общее выражение	Прямоугольные координаты	Полярные координаты
Площадь плоской фигуры	$S=\iint \limits _{G}{d\sigma }$	$\iint \limits _{G}{dxdy}$	$\iint \limits _{G}{rdrd\varphi }$
Масса тонкой плоской пластинки плотностью $\mu$	$m=\iint \limits _{G}{\mu \left(\sigma \right)d\sigma }$	$\iint \limits _{G}{\mu \left(x,y\right)dxdy}$	$\iint \limits _{G}{\mu \left(r,\varphi \right)rdrd\varphi }$
Площадь куска поверхности$^{1)}$	$S=\iint \limits _{G}{\frac {d\sigma }{\cos \gamma }}$	$\iint \limits _{G}{{\sqrt {1+{{\left({\frac {\partial z}{\partial x}}\right)}^{2}}+{{\left({\frac {\partial z}{\partial y}}\right)}^{2}}}}dxdy}$	$\iint \limits _{G}{{\sqrt {{{r}^{2}}+{{r}^{2}}{{\left({\frac {\partial z}{\partial r}}\right)}^{2}}+{{\left({\frac {\partial z}{\partial \varphi }}\right)}^{2}}}}drd\varphi }$
Объем цилиндрического тела, стоящего на плоскости $XOY$	$V=\iint \limits _{G}{zd\sigma }$	$\iint \limits _{G}{zdxdy}$	$\iint \limits _{G}{zrdrd\varphi }$
Момент инерции плоской фигуры$^{2)}$ относительно оси $O{{Z}^{3)}}$	${{I}_{z}}=\iint \limits _{G}{{{r}^{2}}d\sigma }$	$\iint \limits _{G}{\left({{x}^{2}}+{{y}^{2}}\right)dxdy}$	$\iint \limits _{G}{{{r}^{3}}drd\varphi }$
Момент инерции плоской фигуры$^{2)}$ относительно оси $O{{X}^{3)}}$	${{I}_{z}}=\iint \limits _{G}{{{y}^{2}}d\sigma }$	$\iint \limits _{G}{{{y}^{2}}dxdy}$	$\iint \limits _{G}{{{r}^{3}}{{\sin }^{2}}\varphi drd\varphi }$
Координаты центра масс однородной пластинки$^{3)}$	${{x}_{c}}={\frac {1}{S}}{\iint \limits _{G}{xd\sigma }}$ ${{y}_{c}}={\frac {1}{S}}{\iint \limits _{G}{yd\sigma }}$	${\begin{aligned}&{\frac {1}{S}}{\iint \limits _{G}{xdxdy}}\\&{\frac {1}{S}}{\iint \limits _{G}{ydxdy}}\\\end{aligned}}$	${\begin{aligned}&{\frac {1}{S}}{\iint \limits _{G}{{{r}^{2}}\cos \varphi drd\varphi }}\\&{\frac {1}{S}}{\iint \limits _{G}{{{r}^{2}}\sin \varphi drd\varphi }}\\\end{aligned}}$
Примечания	1) Область $G$ — проекция на плоскость $XOY$; в каждую точку области проектируется только одна точка поверхности; $\gamma$ — угол между касательной плоскостью и плоскостью $XOY$. 2) Совмещенной с плоскостью $XOY$. 3) Или, что то же, относительно центра О.

Тройной интеграл

Тройным интегралом называют кратный интеграл с $\ d=3$:

$\iiint \limits _{D}{f\left(P\right)dV}$

где $\ dV$ — элемент объёма в рассматриваемых координатах.

Выражение тройного интеграла через прямоугольные координаты

В прямоугольных координатах тройной интеграл имеет следующий вид:

$\iiint \limits _{D}f(x,y,z)\,dx\,dy\,dz$

где $\ dxdydz$ — элемент объёма в прямоугольных координатах.

Выражение тройного интеграла через цилиндрические координаты

Объем в цилиндрических координатах

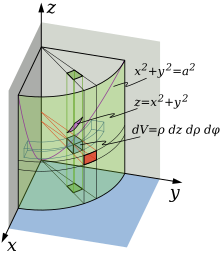
Аналогично в некоторых случаях тройной интеграл проще считать не в прямоугольных, а в цилиндрических координатах. Применим теорему о замене переменных. Соответствующее переходу преобразование имеет вид:

$\left\{{\begin{aligned}&x=r\cos \varphi \\&y=r\sin \varphi \\&z=h\\\end{aligned}}\right.$

Модуль якобиана отображения равен $\ r$. Таким образом получаем, что

$\iiint \limits _{D}{f\left(x,y,z\right)dxdydz}=\iiint \limits _{{D}'}{f\left(r,\varphi ,h\right)rdrd\varphi dh}$

где $rdrd\varphi dh$ — элемент объёма в цилиндрических координатах.

Выражение тройного интеграла через сферические координаты

Объем в сферических координатах

Кроме цилиндрических можно также переходить и в сферические координаты. Применим теорему о замене переменных. Соответствующее переходу преобразование имеет вид:

$\left\{{\begin{aligned}&x=r\sin \theta \cos \varphi \\&y=r\sin \theta \sin \varphi \\&z=r\cos \theta \\\end{aligned}}\right.$

Модуль якобиана отображения равен $\ {{r}^{2}}\sin \theta$. Таким образом получаем, что

$\iiint \limits _{D}{f\left(x,y,z\right)dxdydz}=\iiint \limits _{{D}''}{f\left(r,\varphi ,\theta \right){{r}^{2}}\sin \theta drd\varphi d\theta }$

где ${{r}^{2}}\sin \theta drd\varphi d\theta$ — элемент объёма в сферических координатах.

Приложения тройных интегралов

Наименование величины	Общее выражение	Прямоугольные координаты	Цилиндрические координаты	Сферические координаты
Объем тела	$V=\iiint \limits _{G}{dV}$	$\iiint \limits _{G}{dxdydz}$	$\iiint \limits _{G}{rdrd\varphi dh}$	$\iiint \limits _{G}{{{\rho }^{2}}\sin \theta d\rho d\varphi d\theta }$
Момент инерции геометрического тела относительно оси $OZ$	${{I}_{z}}=\iiint \limits _{G}{{{r}^{2}}dV}$	$\iiint \limits _{G}{\left({{x}^{2}}+{{y}^{2}}\right)dxdydz}$	$\iiint \limits _{G}{{{r}^{3}}drd\varphi dh}$	$\iiint \limits _{G}{{{\rho }^{4}}{{\sin }^{3}}\theta d\rho d\varphi d\theta }$
Масса физического тела с плотностью $\mu$	$m=\iiint \limits _{G}{\mu dV}$	$\iiint \limits _{G}{\mu dxdydz}$	$\iiint \limits _{G}{\mu rdrd\varphi dh}$	$\iiint \limits _{G}{\mu {{\rho }^{2}}\sin \theta d\rho d\varphi d\theta }$
Координаты центра масс однородного тела	${\begin{aligned}&{{x}_{c}}={\frac {1}{V}}{\iiint \limits _{G}{xdV}}\\&{{y}_{c}}={\frac {1}{V}}{\iiint \limits _{G}{ydV}}\\&{{z}_{c}}={\frac {1}{V}}{\iiint \limits _{G}{zdV}}\\\end{aligned}}$	${\begin{aligned}&{\frac {1}{V}}{\iiint \limits _{G}{xdxdydz}}\\&{\frac {1}{V}}{\iiint \limits _{G}{ydxdydz}}\\&{\frac {1}{V}}{\iiint \limits _{G}{zdxdydz}}\\\end{aligned}}$	—	—

Литература

• Выгодский, М. Я. Дифференцирование и интегрирование функций нескольких аргументов // Справочник по высшей математике. — М.: Астрель, АСТ, 2005. — 991 с. — 10 000 экз. — ISBN 5-17-012238-1, 5-271-03651-0.
• Ильин, В. А., Позняк, Э. Г. Глава 2. Двойные и n-кратные интегралы // Основы математического анализа. — 4. — М.: ФИЗМАТЛИТ, 2001. — Т. 2. — 464 с. — (Курс высшей математики и математической физики). — 5000 экз. — ISBN 5-9221-0131-5.
• Кудрявцев, Л. Д. Глава 6. Интегральное исчисление функций многих переменных // Курс математического анализа. — М.: Высшая школа, 1981. — Т. 2. — 584 с.
• Будак, Б. М., Фомин С. В. Кратные интегралы и ряды. — М.: Наука, 1967. — 608 с.