Электрическое поле: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
Mikisavex (обсуждение | вклад) статья переработана так, чтобы минимизировать изложение чисто электростатических аспектов (которые не уничтожены, а перенесены в статью Электростатическое поле), см. тж, СО Метка: ссылка на неоднозначность |
|||
| Строка 1: | Строка 1: | ||
{{другие значения}} |
{{другие значения}} |
||
{{Электродинамика}} |
{{Электродинамика}} |
||
<!-- {{другие значения}} --> |
|||
[[Файл:14. Електрични силови линии.ogv|thumb|right|280px|]] |
|||
<!-- [[Файл:14. Електрични силови линии.ogv|thumb|right|280px|]] --> |
|||
'''Электри́ческое по́ле''' — особый вид материи, который окружает каждый [[электрический заряд]] и оказывает силовое воздействие на все другие заряды, притягивая или отталкивая их<ref>{{cite book | author = Purcell |
|||
'''Электри́ческое по́ле''' — вид материи, который окружает каждый [[электрический заряд]], а также возникает при наличии изменяющегося во времени [[Магнитное поле|магнитного поля]], и оказывает силовое воздействие на все покоящиеся заряды, притягивая или отталкивая их<ref>{{cite book | author = Purcell |
|||
Edward M., Morin David J.| title=''Electricity and Magnetism'' | edition= 3rd | publisher= Cambridge University Press | location = New York| year = 2013 | pages=14–20| isbn= 978-1-107-01402-2}}</ref><ref>Browne, p 225: «… around every charge there is an aura that fills all space. This aura is the electric field due to the charge. The electric field is a vector field… and has a magnitude and direction.»</ref>; также электрическое поле порождается изменяющимся во времени [[Магнитное поле|магнитным полем]]. |
|||
Edward M., Morin David J.| title=''Electricity and Magnetism'' | edition= 3rd | publisher= Cambridge University Press | location = New York| year = 2013 | pages=14–20| isbn= 978-1-107-01402-2}}</ref><ref>Browne, p 225: «… around every charge there is an aura that fills all space. This aura is the electric field due to the charge. The electric field is a vector field… and has a magnitude and direction.»</ref>. |
|||
Электрическое поле математически определяется как [[Векторное поле|векторное поле,]] которое связывает с каждой точкой в пространстве [[Сила|силу]] (электростатическую, или [[Закон Кулона|кулоновскую]]) на единицу [[Электрический заряд|заряда,]] приложенную к бесконечно малому положительному [[Пробное тело|пробному заряду,]] покоящемуся в этой точке<ref>{{Cite book|author=Richard Feynman|title=The Feynman Lectures on Physics Vol II|publisher=Addison Wesley Longman|year=1970|pages=1—3,1-4|isbn=978-0-201-02115-8|url=http://www.feynmanlectures.caltech.edu/II_01.html}}</ref><ref>{{Cite book|author=Purcell|title=''Electricity and Magnetism''|publisher=Cambridge University Press|year=2013|pages=15–16|isbn=978-1-107-01402-2}}</ref><ref name="Serway">{{Cite book|author=Serway|title=College Physics, 10th Ed.|publisher=Cengage Learning|pages=532–533|url=https://books.google.com/books?id=xETAAgAAQBAJ&q=work+energy+capacitor&pg=PA522|isbn=978-1305142824}}</ref>. Величина указанного векторного поля называется его [[Напряжённость электрического поля|напряжённостью]] (обозначение: <math>\ |
Электрическое поле математически определяется как [[Векторное поле|векторное поле,]] которое связывает с каждой точкой в пространстве [[Сила|силу]] (электростатическую, или [[Закон Кулона|кулоновскую]]) на единицу [[Электрический заряд|заряда,]] приложенную к бесконечно малому положительному [[Пробное тело|пробному заряду,]] покоящемуся в этой точке<ref>{{Cite book|author=Richard Feynman|title=The Feynman Lectures on Physics Vol II|publisher=Addison Wesley Longman|year=1970|pages=1—3,1-4|isbn=978-0-201-02115-8|url=http://www.feynmanlectures.caltech.edu/II_01.html}}</ref><ref>{{Cite book|author=Purcell|title=''Electricity and Magnetism''|publisher=Cambridge University Press|year=2013|pages=15–16|isbn=978-1-107-01402-2}}</ref><ref name="Serway">{{Cite book|author=Serway|title=College Physics, 10th Ed.|publisher=Cengage Learning|pages=532–533|url=https://books.google.com/books?id=xETAAgAAQBAJ&q=work+energy+capacitor&pg=PA522|isbn=978-1305142824}}</ref>. Величина указанного векторного поля называется его [[Напряжённость электрического поля|напряжённостью]] (обозначение: <math>\mathbf{E}</math>). В системе [[Производные единицы СИ|СИ]] единица измерения напряжённости электрического поля: [[вольт]] на [[метр]] (В/м) или, что то же самое, [[Ньютон (единица измерения)|ньютон]] на [[кулон]] (Н/Кл). |
||
Электрические и магнитные поля рассматриваются как проявления более общей физической реальности — [[Электромагнетизм|электромагнитного поля]], ответственного за одно из [[Фундаментальные взаимодействия|фундаментальных взаимодействий]] природы (наряду с гравитационным, сильным и слабым). |
Электрические и магнитные поля рассматриваются как проявления более общей физической реальности — [[Электромагнетизм|электромагнитного поля]], ответственного за одно из [[Фундаментальные взаимодействия|фундаментальных взаимодействий]] природы (наряду с гравитационным, сильным и слабым). Частным случаем электрического поля является [[Электростатическое поле|электростатическое]]. |
||
Электрические поля важны во многих областях [[Физика|физики]] и используются практически в электротехнике. [[Атомная физика|Например, в атомной физике]] и [[Химия|химии]] электрическое поле |
Электрические поля важны во многих областях [[Физика|физики]] и используются практически в электротехнике. [[Атомная физика|Например, в атомной физике]] и [[Химия|химии]] электрическое поле — это сила удерживающая [[атомное ядро]] и [[электрон]]ы вместе в атомах. Эта сила отвечает за [[Химическая связь|химические связи]] между атомами, в результате которых [[Молекула|образуются молекулы]]. Другие использования электрических полей включают обнаружение движения посредством ёмкостных методов и растущее число диагностических и терапевтических медицинских применений. |
||
== Качественное описание == |
|||
== Описание == |
|||
Под электрическим полем одновременно понимаются |
|||
[[Файл:VFPt_image_charge_plane_horizontal.svg|мини|250x250пкс| Электрическое поле положительного точечного [[Электрический заряд|электрического заряда,]] подвешенного над полубесконечным проводящим материалом. Поле изображается [[Силовые линии векторного поля|линиями электрического поля]], которые указывают направление электрического поля в пространстве.]] |
|||
* вид материи, оказывающий силовое воздействие на электрические заряды, в том числе покоящиеся; |
|||
Электрическое поле определяется в каждой точке пространства как сила (на единицу заряда), которую испытывает [[Бесконечно малая и бесконечно большая|исчезающе малый]] положительный [[Пробное тело|пробный заряд,]] помещённый в этой точке.<ref name="uniphysics">{{Citation|first=Francis|last=Sears|title=University Physics, Sixth Edition|publisher=Addison Wesley|year=1982|isbn=0-201-07199-1}}</ref> {{Rp|469–70}} Поскольку электрическое поле определяется через понятие [[Сила|силы]], а сила является [[Вектор (геометрия)|вектором]] (то есть имеет и [[Величина (математика)|величину,]] и направление), из этого следует, что электрическое поле будет [[Векторное поле|векторным полем]] . {{Rp|469–70}} Векторные поля такого вида иногда называют [[Силовое поле (физика)|силовыми полями]]. Электрическое поле действует между двумя зарядами подобно тому, как [[гравитационное поле]] действует между двумя обладающими [[масса|массой]] телами, расположенными на каком-то расстоянии, поскольку они оба подчиняются [[Закон обратных квадратов|закону обратных квадратов]].<ref name="Umashankar">{{Citation|first=Korada|last=Umashankar|title=Introduction to Engineering Electromagnetic Fields|year=1989|publisher=World Scientific|isbn=9971-5-0921-0}}</ref> [[Закон Кулона]] гласит, что для стационарных зарядов электрическое поле изменяется в зависимости от заряда источника и изменяется обратно пропорционально квадрату расстояния от источника. Это означает, что при удвоении заряда источника, электрическое поле удваивается, а если пробный заряд отодвинуть вдвое дальше от источника, то поле в этой точке будет вчетверо слабее его первоначальной силы. |
|||
* физическая векторная величина [[Напряжённость электрического поля|напряжённости электрического поля]]. |
|||
Вторая из указанных трактовок несколько сужает предмет, поскольку напряжённость выступает основной, но не единственно возможной характеристикой данного вида материи (иной вариант характеризации — использование потенциалов). |
|||
=== Регистрация и некоторые свойства === |
|||
Электрическое поле можно изобразить с помощью набора [[Силовые линии векторного поля|линий]], направление которых совпадает с направлением поля в этой точке. Эта концепция была введена [[Фарадей, Майкл|Майклом Фарадеем]]<ref name="elec_princ_p73">{{Citation|author=Morely & Hughes|title=Principles of Electricity, Fifth edition|isbn=0-582-42629-4}}</ref>, чей термин «силовые линии» все ещё употребляется. Такая интерпретация полезна тем, что [[напряжённость электрического поля]] пропорциональна плотности линий.<ref name="Tou">{{Cite book|author=Tou|title=Visualization of Fields and Applications in Engineering|publisher=John Wiley and Sons|pages=64|url=https://books.google.com/books?id=4kjP1ALPTfUC&q=%22field+line%22+vector+field+tangent&pg=PT64|isbn=9780470978467}}</ref> Силовые линии стационарных зарядов имеют несколько важных свойств: линии поля начинаются от положительных зарядов и заканчиваются отрицательными зарядами, они входят во все хорошие проводники под прямым углом, и они никогда не пересекаются и не замыкаются между собой. Линии поля удобны для схематичного представления; но поле фактически пронизывает все пространство между линиями. Можно нарисовать больше или меньше линий в зависимости от точности, с которой желательно представить поле. Раздел физики, изучающий электрические поля стационарных зарядов, называется [[Электростатика|электростатикой]]. |
|||
Напряжённость электрического поля определяется в каждой точке пространства как сила (на единицу заряда), которую испытывает [[Бесконечно малая и бесконечно большая|исчезающе малый]] положительный [[Пробное тело|пробный заряд,]] помещённый в эту точку.<ref name="uniphysics">{{Citation|first=Francis|last=Sears|title=University Physics, Sixth Edition|publisher=Addison Wesley|year=1982|isbn=0-201-07199-1}}</ref> {{Rp|469–70}} Поскольку электрическое поле дефинируется через понятие [[Сила|силы]], а сила является [[Вектор (геометрия)|вектором]] (то есть имеет и [[Величина (математика)|величину,]] и направление), электрическое поле является [[Векторное поле|векторным полем]] . {{Rp|469–70}} Векторные поля такого вида иногда называют [[Силовое поле (физика)|силовыми полями]]. Практически, роль регистратора электрического поля может выполнить заряженное тело малых размеров. |
|||
В общем случае поле зависит от трёх пространственных координат и времени: <math>\mathbf{E}=\mathbf{E}(\mathbf{r}, t) = \mathbf{E}(x,\,y,\,z,\,t)</math>. |
|||
[[Закон электромагнитной индукции Фарадея|Закон Фарадея]] описывает взаимосвязь между изменяющимися во времени магнитным и электрическим полями. Один из способов сформулировать закон Фарадея состоит в том, что [[Ротор (дифференциальный оператор)|ротор]] электрического поля равен отрицательной частной [[Производная по времени|производной]] магнитного поля по времени.<ref name="griffiths">{{Cite book|last=Griffiths, David J. (David Jeffery), 1942-|title=Introduction to electrodynamics|date=1999|publisher=Prentice Hall|isbn=0-13-805326-X|edition=3rd|location=Upper Saddle River, N.J.}}</ref> {{Rp|327}} В отсутствие изменяющегося во времени магнитного поля, электрическое поле называется [[Потенциальное векторное поле|потенциальным]] (то есть безроторным). {{Rp|24,90–91}} Это означает, что существует два вида электрического поля: [[электростатическое поле]] и электрическое поле, возникающее вследствие изменения во времени магнитного поля. {{Rp|305–307}} Электростатическое поле рассматривается в электростатике, но при изменяющемся во времени магнитном поле необходимо рассматривать [[электромагнитное поле]]. Раздел физики, изучающий изменяющиеся во времени магнитные и электрические поля, называется [[Электромагнетизм|электродинамикой]]. |
|||
Электрическое поле, в зависимости от способа его создания (см. ниже), может быть или не быть [[Потенциальное поле|потенциальным]]. [[Электростатическое поле]] потенциально всегда. |
|||
== Математическая формулировка == |
|||
Электрические поля вызываются [[Электрический заряд|электрическими зарядами]], описываемыми законом [[Теорема Гаусса|Гаусса]]<ref>Purcell, p 25: «Gauss’s Law: the flux of the electric field E through any closed surface… equals 1/e times the total charge enclosed by the surface.»</ref>, и изменяющимися во времени [[Магнитное поле|магнитными полями]], описываемыми [[Закон электромагнитной индукции Фарадея|законом электромагнитной индукции Фарадея]].<ref>Purcell, p 356: «Faraday’s Law of Induction.»</ref> Этих законов достаточно, для определения поведения электрического поля в вакууме. Однако, поскольку магнитное поле описывается как функция электрического поля, то уравнения для обоих полей связаны и вместе образуют [[Уравнения Максвелла|уравнения Максвелла,]] которые описывают оба поля как функцию зарядов и [[Электрический ток|токов]]. |
|||
Достаточно часто электрическое поле сосуществует с магнитным полем, причём имеет место взаимопревращение переменных электрического и магнитного полей, например в [[Электромагнитная волна|электромагнитной волне]]. |
|||
=== Электростатика === |
|||
В частном случае [[Стационарное состояние (математика)|стационарного состояния]] (стационарные заряды и токи) индуктивный эффект Максвелла — Фарадея исчезает. Полученные два уравнения (закон Гаусса <math>\nabla \cdot \mathbf{E} = \frac{\rho}{\varepsilon_0}</math> и закон Фарадея без индукционного члена <math>\nabla \times \mathbf{E} = 0</math>), вместе взятые, эквивалентны [[Закон Кулона|закону Кулона]], который гласит, что частица с электрическим зарядом <math>q_1</math> в точке <math>\boldsymbol{x}_1</math> (радиус-вектор) действует с силой на частицу с зарядом <math>q_0</math> в точке <math>\boldsymbol{x}_0</math>:<ref>Purcell, p7: "… the interaction between electric charges ''at rest'' is described by Coulomb’s Law: two stationary electric charges repel or attract each other with a force proportional to the product of the magnitude of the charges and inversely proportional to the square of the distance between them.</ref> |
|||
Величина поля зависит от выбора [[Система отсчёта|системы отсчета]], переход от одной [[Инерциальная система отсчета|инерциальной системы отсчёта]] к другой осуществляется с помощью [[преобразования Лоренца|преобразований Лоренца]], в которых совместно задействуются и электрическая, и магнитная компоненты электромагнитного поля<ref>См. параграф [https://online.mephi.ru/courses/physics/electricity/data/course/6/6.7.html Преобразования Лоренца для электромагнитного поля] (ф-лы 6.38) курса «Электричество и магнетизм» на сайте [[Московский инженерно-физический институт|МИФИ]], кафедра общей физики.</ref>. Электрическое поле [[инвариант]]ом преобразований Лоренца не является. |
|||
: <math> |
|||
\boldsymbol{F} = {1\over 4\pi\varepsilon_0}{q_1q_0 \over (\boldsymbol{x}_1-\boldsymbol{x}_0)^2}\hat \boldsymbol{r}_{1,0} |
|||
</math>, |
|||
где <math>\boldsymbol{r}_{1,0}</math> — [[единичный вектор]] в направлении от точки <math>\boldsymbol{x}_1</math> в точку <math>\boldsymbol{x}_0</math>, а {{Math|''ε''{{sub|0}}}} — [[электрическая постоянная]] (также известная как «абсолютная диэлектрическая проницаемость свободного пространства») с единицами измерения C <sup>2</sup> м <sup>−2</sup> Н <sup>−1</sup>. Если заряды находятся не в вакууме, а в однородном диэлектрике, то <math>\varepsilon_0</math> заменяется на [[Диэлектрическая проницаемость|диэлектрическую проницаемость]] среды <math>\varepsilon_0\varepsilon</math>. |
|||
За некоторыми исключениями, электрическое поле подчиняется [[Принцип суперпозиции|принципу суперпозиции]], то есть поле нескольких источников есть сумма полей, создаваемых источниками. Это утверждение может быть проверено эмпирически и соответствует теоретическим моделям (см. ниже). |
|||
Когда заряды <math>q_0</math> и <math>q_1</math> имеют одинаковые знаки, эта сила положительна и направлена от другого заряда, то есть частицы отталкиваются друг от друга. Когда заряды имеют разные знаки, сила отрицательна, что указывает на притяжение частиц. Чтобы упростить расчет [[Закон Кулона|кулоновской силы]] для любого заряда в точке <math>\boldsymbol{x}_0</math>, это выражение можно разделить на <math>q_0</math> оставив выражение, которое зависит только от другого заряда (заряда ''источника'')<ref name="Purcell">{{cite book |
|||
| last1 = Purcell |
|||
| first1 = Edward |
|||
| title = Electricity and Magnetism, 2nd Ed. |
|||
| publisher = Cambridge University Press |
|||
| date = 2011 |
|||
| pages = 8–9 |
|||
| url = https://books.google.com/books?id=Z3bkNh6h4WEC&pg=PA8 |
|||
| isbn = 978-1139503556 |
|||
}}</ref> |
|||
=== Способы создания === |
|||
: <math> |
|||
{{main|Закон Кулона|Закон электромагнитной индукции}} |
|||
\boldsymbol{E}(\boldsymbol{x}_0) = {\boldsymbol{F} \over q_0} = {1\over 4\pi\varepsilon_0}{q_1 \over (\boldsymbol{x}_1-\boldsymbol{x}_0)^2}\hat \boldsymbol{r}_{1,0} |
|||
Электрическое поле может быть создано |
|||
</math> |
|||
* электрическим зарядом; |
|||
* переменным во времени магнитным полем. |
|||
[[Закон Кулона]] гласит, что электрическое поле стационарных зарядов в вакууме или однородной среде изменяется пропорционально заряду источника и обратно пропорционально квадрату расстояния от источника. Это означает, что при удвоении заряда источника поле удваивается, а если пробный заряд отодвинуть вдвое дальше от источника, то поле в этой точке будет вчетверо слабее его первоначальной силы. Электрическое поле действует между двумя зарядами подобно тому, как [[гравитационное поле]] действует между двумя обладающими [[масса|массой]] телами, расположенными на каком-то расстоянии, поскольку они оба подчиняются [[Закон обратных квадратов|закону обратных квадратов]]<ref name="Umashankar">{{Citation|first=Korada|last=Umashankar|title=Introduction to Engineering Electromagnetic Fields|year=1989|publisher=World Scientific|isbn=9971-5-0921-0}}</ref>. |
|||
Это ''электрическое поле'' в точке <math>\boldsymbol{x}_0</math> создаваемое точечным зарядом <math>q_1</math>. Она представляет собой [[Вектор-функция|векторную функцую]], которая равна кулоновской силе на единицу заряда, испытываемой положительным точечным зарядом в точке <math>\boldsymbol{x}_0</math>. Поскольку эта формула дает величину и направление электрического поля в любой точке <math>\boldsymbol{x}_0</math> пространства (кроме места нахождения самого заряда, <math>\boldsymbol{x}_1</math>, где оно становится бесконечным), то оно определяет [[векторное поле]]. Из приведенной выше формулы видно, что электрическое поле, создаваемое точечным зарядом, везде направлено от заряда, если он положительный, и в сторону заряда, если он отрицательный, и его величина уменьшается [[Закон обратных квадратов|пропорционально обратному квадрату]] расстояния от заряда. |
|||
[[Закон электромагнитной индукции Фарадея|Закон Фарадея]] описывает взаимосвязь между изменяющимися во времени магнитным и электрическим полями. Один из способов сформулировать закон Фарадея — [[Ротор (дифференциальный оператор)|ротор]] электрического поля равен отрицательной частной [[Производная по времени|производной]] магнитного поля по времени.<ref name="griffiths">{{Cite book|last=Griffiths, David J. (David Jeffery), 1942-|title=Introduction to electrodynamics|date=1999|publisher=Prentice Hall|isbn=0-13-805326-X|edition=3rd|location=Upper Saddle River, N.J.}}</ref> {{Rp|327}} В отсутствие изменяющегося во времени магнитного поля, электрическое поле [[Потенциальное векторное поле|потенциально]] (то есть является безроторным). {{Rp|24,90–91}} |
|||
Кулоновская сила действующая на заряд величиной <math>q</math> в любой точке пространства равна произведению заряда и электрического поля в этой точке |
|||
=== Графическое представление === |
|||
: <math>\boldsymbol{F} = q\boldsymbol{E}</math> |
|||
{{main|Силовые линии векторного поля}} |
|||
[[Файл:VFPt_image_charge_plane_horizontal.svg|мини|250x250пкс| Электрическое поле положительного точечного [[Электрический заряд|электрического заряда,]] подвешенного над полубесконечным проводящим материалом. Поле изображается [[Силовые линии векторного поля|линиями электрического поля]], которые указывают направление электрического поля в пространстве.]] |
|||
Электрическое поле можно изобразить с помощью набора [[Силовые линии векторного поля|линий]], в каждой своей точке сонаправленных с полем в этой точке. Данная концепция была введена [[Фарадей, Майкл|Майклом Фарадеем]]<ref name="elec_princ_p73">{{Citation|author=Morely & Hughes|title=Principles of Electricity, Fifth edition|isbn=0-582-42629-4}}</ref>, чей термин «силовые линии» употребляется и ныне. Такое представление полезно тем, что [[напряжённость электрического поля]] тем больше, чем гуще проходят линии<ref name="Tou">{{Cite book|author=Tou|title=Visualization of Fields and Applications in Engineering|publisher=John Wiley and Sons|pages=64|url=https://books.google.com/books?id=4kjP1ALPTfUC&q=%22field+line%22+vector+field+tangent&pg=PT64|isbn=9780470978467}}</ref>. Для нестационарного электрического поля картина его силовых линий может быть изображена для выбранного конкретного момента времени. |
|||
Обычно к построению силовых линий прибегают для стационарного ([[Электростатика|электростатического]]) случая. Силовые линии стационарных зарядов начинаются от положительных зарядов и заканчиваются отрицательными зарядами, они входят во все хорошие проводники под прямым углом, и они никогда не пересекаются и не замыкаются. Линии поля удобны для схематичного представления; но поле фактически пронизывает всё пространство между линиями. Можно нарисовать больше или меньше линий в зависимости от желаемой степени детализации. |
|||
Единицы электрического поля в системе [[Международная система единиц|СИ]] — [[Ньютон (единица измерения)|ньютон]] на [[кулон]] (Н / Кл) или [[вольт]] на [[метр]] (В / м); в основных единицах системы [[Основные единицы СИ|СИ]] это кг⋅м⋅с<sup>−3</sup> ⋅A<sup>−1.</sup> |
|||
== Количественное описание == |
|||
=== Принцип суперпозиции === |
|||
Из-за [[Линейное дифференциальное уравнение|линейности]] [[Уравнения Максвелла|уравнений Максвелла]] электрические поля удовлетворяют [[Принцип суперпозиции|принципу суперпозиции]], который гласит, что полное электрическое поле в точке от распределённых в пространстве зарядов равно векторной сумме электрических полей создаваемых в этой точке отдельными зарядами. Этот принцип полезен при расчете поля, создаваемого множественными точечными зарядами. Если заряды <math>q_1, q_2, ..., q_n</math> неподвижно расположены в точках <math>\mathbf{x}_1,\mathbf{x}_2,...\mathbf{x}_n</math>, то при отсутствии токов принцип суперпозиции гласит, что результирующее поле является суммой полей, генерируемых каждой частицей, и описывается законом Кулона: |
|||
Расчёт электрического поля можно проводить аналитическими<ref>''Гринберг Г. А.'' Избранные вопросы математической теории электрических и магнитных явлений. — М.: АН СССР, 1948. — 727 с.</ref><ref>''Миролюбов Н. Н., Костенко М. В., Левинштейн М. Л.'' Методы расчета электростатических полей. — М.: Высшая школа, 1963. — 416 с.</ref><ref>''Смайт В.'' Электростатика и электродинамика. — М.: ИЛ, 1954. — 604 с.</ref> и численными<ref name = "Kole">''Колечицкий Е. С.'' Расчет электрических полей устройств высокого напряжения. — М.: Энергоатомиздат, 1983. — 168 с.</ref> методами. Аналитические методы удаётся применить лишь в простейших случаях, на практике в основном используются численные методы. Они включают: метод сеток или [[метод конечных разностей]]; вариационные методы; [[метод конечных элементов]]; метод интегральных уравнений; метод эквивалентных зарядов<ref name = "Kole"></ref>. Ключевые физические формулы представлены ниже. |
|||
: <math> |
|||
\boldsymbol{E}(\boldsymbol{x}) = \boldsymbol{E}_1(\boldsymbol{x}) + \boldsymbol{E}_2(\boldsymbol{x}) + \boldsymbol{E}_3(\boldsymbol{x}) + \cdots |
|||
= </math> |
|||
:: <math> ={1\over 4\pi\varepsilon_0}{q_1 \over (\boldsymbol{x}_1-\boldsymbol{x})^2}\hat \boldsymbol{r}_1 |
|||
+ {1\over 4\pi\varepsilon_0}{q_2 \over (\boldsymbol{x}_2-\boldsymbol{x})^2}\hat \boldsymbol{r}_2 + {1\over 4\pi\varepsilon_0}{q_3 \over (\boldsymbol{x}_3-\boldsymbol{x})^2}\hat \boldsymbol{r}_3 + \cdots |
|||
</math> |
|||
: <math> |
|||
\boldsymbol{E}(\boldsymbol{x}) = {1\over 4\pi\varepsilon_0} \sum_{k=1}^N {q_k \over (\boldsymbol{x}_k-\boldsymbol{x})^2}\hat \boldsymbol{r}_k |
|||
</math>, |
|||
где <math>\boldsymbol{\hat r_k}</math> — [[единичный вектор]] направленный от точки <math>\boldsymbol{x}_k</math> в точку <math>\boldsymbol{x}</math> . |
|||
=== Базовые уравнения === |
|||
=== Непрерывное распределение заряда === |
|||
{{main|Уравнения Максвелла}} |
|||
Принцип суперпозиции позволяет рассчитать электрическое поле от непрерывного распределения заряда <math>\rho(\boldsymbol{x})</math> (где <math>\rho</math> — [[плотность заряда]] в кулонах на кубический метр). Учитывая заряд <math>\rho(\boldsymbol{x}')dV</math> в каждом небольшом объёме пространства <math>dV</math> в точке <math>\boldsymbol{x}'</math> в виде точечного заряда, то электрическое поле <math>d\boldsymbol{E}(\boldsymbol{x})</math> в точке <math>\boldsymbol{x}</math> можно рассчитать как |
|||
Основными уравнениями теории электромагнетизма являются [[уравнения Максвелла]]. Всего их четыре: |
|||
: <math>\nabla\cdot\mathbf{D}= \rho,\qquad\qquad \nabla\cdot\mathbf{B}=0</math> |
|||
: <math>\nabla\times\mathbf{E}=-\frac{\partial\mathbf{B}}{\partial t},\qquad\nabla\times\mathbf{H}= \mathbf{j}+\frac{\partial\mathbf{D}}{\partial t}</math>. |
|||
В одно из этих уравнений напряжённость электрического поля <math>\boldsymbol{E}</math> входит в явном виде, ещё в два — через вектор [[Электрическое смещение|электрического смещения]] <math>\boldsymbol{D}</math>. Кроме названных величин, в уравнениях фигурируют [[Вектор магнитной индукции|индукция]] <math>\boldsymbol{B}</math> и [[Напряжённость магнитного поля|напряжённость]] <math>\boldsymbol{H}</math> магнитного поля. Прочие обозначения: <math>\boldsymbol{j}</math> — [[плотность электрического тока]] (А/м<sup>2</sup>), <math>\rho</math> — [[плотность заряда]] (Кл/м<sup>3</sup>), <math>\nabla</math> — [[оператор набла]], <math>t</math> — время. Это так называемая [[Уравнения Максвелла#Уравнения Максвелла в дифференциальной форме|дифференциальная форма]] уравнений Максвелла. |
|||
=== Заряд в базовых уравнениях === |
|||
: <math> |
|||
{{main|Плотность электрического заряда}} |
|||
d\boldsymbol{E}(\boldsymbol{x}) = {1\over 4\pi\varepsilon_0}{\rho(\boldsymbol{x}')dV \over (\boldsymbol{x}'-\boldsymbol{x})^2}\hat \boldsymbol{r}' |
|||
При работе с уравнениями электромагнетизма лучше использовать непрерывные функции и распределённый заряд. Так, в выписанное выше выражение для <math>\nabla\cdot\mathbf{D}</math> электрический заряд входит именно в виде его объёмной плотности. При необходимости, точечный заряд <math>q</math>, расположенный в месте с радиус-вектором <math>\mathbf{r_0}</math>, математически можно описать как плотность заряда <math>\rho(\mathbf{r})=q\delta(\mathbf{r-r_0})</math>, где используется [[Дельта-функция|дельта-функция Дирака]] (в трех измерениях). |
|||
</math> |
|||
Но уравнения Максвелла могут быть переписаны в [[Уравнения Максвелла#Уравнения Максвелла в интегральной форме|интегральной форме]], и тогда можно оперировать такими величинами, как заряд или ток (а не плотность заряда, плотность тока). Кроме того, есть физические ситуации, когда традиционно удобнее учитывать «штучность», «дискретность» зарядов: например, в некоторых моделях можно описывать [[электрон]]ы как точечные источники, плотность заряда которых бесконечна на бесконечно малом участке пространства. Также любое непрерывное распределение заряда можно аппроксимировать множеством небольших точечных зарядов. |
|||
где <math>\hat \boldsymbol{r}'</math> это единичный вектор, направленный от <math>\boldsymbol{x}'</math> к <math>\boldsymbol{x}</math>. Полное электрическое поле находится путем «сложения» вкладов от всех малых объёмов путем [[Интеграл|интегрирования]] по объёму распределения заряда <math>\rho(x')</math> : |
|||
=== Принцип суперпозиции === |
|||
{{main|Принцип суперпозиции}} |
|||
Ввиду [[Линейное дифференциальное уравнение|линейности]] [[Уравнения Максвелла|уравнений Максвелла]], электрические поля удовлетворяют [[Принцип суперпозиции|принципу суперпозиции]], который гласит, что полное электрическое поле в точке <math>\boldsymbol{r}</math>, создаваемое несколькими источниками, есть сумма полей этих источников: |
|||
: <math> |
: <math> |
||
\boldsymbol{E}(\boldsymbol{ |
\boldsymbol{E}(\boldsymbol{r}) = \boldsymbol{E}_1(\boldsymbol{r}) + \boldsymbol{E}_2(\boldsymbol{r}) + \boldsymbol{E}_3(\boldsymbol{r}) + \cdots |
||
= \sum_{k=1}^N \boldsymbol{E}_k(\boldsymbol{r}) </math>, |
|||
</math> |
|||
где индекс <sub>k</sub> пробегает все <math>N</math> источников. В их роли, в простейшем случае, выступают [[Точечный электрический заряд|точечные заряды]], поле каждого из которых рассчитывается по [[Закон Кулона|закону Кулона]]. В более сложных случаях источниками могут являться распределённые в пространстве заряды или переменные магнитные поля. |
|||
Принцип суперпозиции может нарушаться для нелинейных, в первую очередь [[Сегнетоэлектричество|сегнетоэлектрических]], сред, [[диэлектрическая проницаемость]] которых зависит от величины поля и от предыстории образца. |
|||
Аналогичные уравнения записываются для поверхностного заряда с непрерывным распределением заряда <math>\sigma(\boldsymbol{x})</math> где <math>\sigma</math> это плотность заряда в кулонах на квадратный метр |
|||
=== Потенциалы электрического поля === |
|||
: <math> |
|||
{{main|Электрический потенциал|Векторный потенциал электромагнитного поля}} |
|||
\boldsymbol{E}(\boldsymbol{x}) = {1\over 4\pi\varepsilon_0}\iint\limits_S \,{\sigma(\boldsymbol{x}')dA \over (\boldsymbol{x}'-\boldsymbol{x})^2}\hat \boldsymbol{r}' |
|||
Если система статична, так что магнитные поля не меняются во времени, то по закону Фарадея электрическое поле [[Потенциальное векторное поле|потенциально]]. В этом случае можно задать [[Электростатический потенциал|электрический потенциал]], то есть функцию <math>\varphi</math> такую, что <math> \mathbf{E} = -\nabla \varphi </math> .<ref>{{Cite web|url=http://physicspages.com/pdf/Griffiths%20EM/Griffiths%20Problems%2002.20.pdf|title=Curl & Potential in Electrostatics|author=gwrowe|website=physicspages.com|date=2011-10-08|archive-url=https://web.archive.org/web/20190322101416/http://physicspages.com/pdf/Griffiths%20EM/Griffiths%20Problems%2002.20.pdf|archive-date=2019-03-22|access-date=2020-11-02}}</ref> Это аналог [[Гравитационный потенциал|гравитационного потенциала]]. Разница между электрическим потенциалом в двух точках пространства называется [[Электрическое напряжение|разностью потенциалов]] (или напряжением) между этими двумя точками. |
|||
</math> |
|||
Однако в общем случае электрическое поле нельзя описать независимо от магнитного поля. Учитывая [[векторный потенциал электромагнитного поля]] '''A''', определённый как <math> \mathbf{B} = \nabla \times \mathbf{A} </math>, можно задать электрический потенциал <math> \varphi</math> в виде |
|||
и для линейных зарядов с непрерывным распределением заряда <math>\lambda(\boldsymbol{x})</math> где <math>\lambda</math> — плотность заряда в кулонах на метр. |
|||
: <math> \mathbf{E} = - \nabla \varphi - \frac { \partial \mathbf{A} } { \partial t }</math>, |
|||
: <math> |
|||
\boldsymbol{E}(\boldsymbol{x}) = {1\over 4\pi\varepsilon_0}\int\limits_P \,{\lambda(\boldsymbol{x}')dL \over (\boldsymbol{x}'-\boldsymbol{x})^2}\hat \boldsymbol{r}' |
|||
</math> |
|||
где <math>\nabla \varphi</math> — [[градиент]] электрического потенциала и <math>\partial \mathbf{A}/\partial t</math> — [[частная производная]] от '''''A''''' по времени. |
|||
=== Электрический потенциал === |
|||
Если система статична, так что магнитные поля не меняются во времени, то по закону Фарадея электрическое поле [[Потенциальное векторное поле|потенциально]]. В этом случае можно задать [[Электростатический потенциал|электрический потенциал]], то есть функцию <math>\Phi</math> такую, что <math> \mathbf{E} = -\nabla \Phi </math> .<ref>{{Cite web|url=http://physicspages.com/pdf/Griffiths%20EM/Griffiths%20Problems%2002.20.pdf|title=Curl & Potential in Electrostatics|author=gwrowe|website=physicspages.com|date=2011-10-08|archive-url=https://web.archive.org/web/20190322101416/http://physicspages.com/pdf/Griffiths%20EM/Griffiths%20Problems%2002.20.pdf|archive-date=2019-03-22|access-date=2020-11-02}}</ref> Это аналог [[Гравитационный потенциал|гравитационного потенциала]]. Разница между электрическим потенциалом в двух точках пространства называется [[Электрическое напряжение|разностью потенциалов]] (или напряжением) между этими двумя точками. |
|||
Упоминавшийся выше [[Закон электромагнитной индукции Фарадея|закон индукции Фарадея]] можно получить, взяв [[Ротор (дифференциальный оператор)|ротор]] от этого уравнения<ref>{{Cite book|title=Maxwell's Equations|last=Huray|isbn=978-0-470-54276-7|url=https://books.google.com/books?id=0QsDgdd0MhMCp}}</ref>: <math>\nabla \times \mathbf{E} = - \partial (\nabla \times \mathbf{A})/\partial t= -\partial \mathbf{B}/\partial t</math>, что ''a posteriori'' подтверждает правильность выбранной формы для '''E.''' |
|||
Однако в общем случае электрическое поле нельзя описать независимо от магнитного поля. Учитывая [[Векторный потенциал электромагнитного поля|вектор магнитного потенциала]] '''A''', определённый как <math> \mathbf{B} = \nabla \times \mathbf{A} </math>, можно задать электрический потенциал <math> \Phi</math> в виде |
|||
Уравнения Максвелла [[Векторный потенциал электромагнитного поля#Уравнения Максвелла|могут быть переписаны]] с использованием скалярного (<math>\varphi</math>) и векторного (<math>\mathbf{A}</math>) потенциалов, что иногда удобно для вычислений. |
|||
: <math> \mathbf{E} = - \nabla \Phi - \frac { \partial \mathbf{A} } { \partial t }</math> |
|||
== Виды электрических полей == |
|||
где <math>\nabla \Phi</math> — [[градиент]] электрического потенциала и <math>\frac { \partial \mathbf{A} } { \partial t }</math> — [[частная производная]] от '''''A''''' по времени. |
|||
=== Электростатические поля === |
|||
{{main|Электростатическое поле}} |
|||
Электростатические поля — это электрические поля, которые не меняются со временем, существующие, когда заряды неподвижны, а токи, если они есть, постоянны. В этом случае [[закон Кулона]] |
|||
: <math>\mathbf{F}=q^*\left(\frac{Q}{4\pi\varepsilon_0\varepsilon}\frac{\mathbf{\mathbf{r}}}{|\mathbf{r}|^3}\right)=q^*\mathbf{E}(\mathbf{r}) |
|||
</math> |
|||
для силы действия заряда <math>Q</math>, расположенного в начале координат и создающего поле <math>\mathbf{E}</math>, на находящийся в точке <math>\mathbf{r}</math> пробный заряд <math>q^*</math> (или обобщение этого закона для распределённых зарядов) полностью описывает электрическое поле.<ref>Purcell, pp. 5-7.</ref> Однако сфера применения закона Кулона ограничивается задачами для вакуума или сред с фиксированной [[Диэлектрическая проницаемость|диэлектрической проницаемостью]] <math>\varepsilon</math>; при наличии же неоднородных диэлектриков (с <math>\varepsilon\ne\,</math>const<math>(\mathbf{r})</math>), используется более сложный математический аппарат, в том числе решение [[Уравнение Пуассона|уравнения Пуассона]]. |
|||
Закон Кулона, описывающий взаимодействие электрических зарядов, похож на [[Классическая теория тяготения Ньютона|закон всемирного тяготения Ньютона]], что предполагает логическое сходство между электрическим полем '''E''' и гравитационным полем '''g''' или связанными с ними потенциалами<ref>{{Cite journal|author=Salam|first=Abdus|title=Quarks and leptons come out to play|journal=New Scientist|date=16 December 1976|volume=72|url=https://books.google.com/books?id=WIbyn2jxGhoC&pg=PA652}}</ref>. |
|||
[[Закон электромагнитной индукции Фарадея|Закон индукции Фарадея]] можно получить, взяв [[Ротор (дифференциальный оператор)|ротор]] от этого уравнения<ref>{{Cite book|title=Maxwell's Equations|last=Huray|isbn=978-0-470-54276-7|url=https://books.google.com/books?id=0QsDgdd0MhMCp}}</ref> |
|||
=== Электродинамические поля === |
|||
: <math>\nabla \times \mathbf{E} = -\frac{\partial (\nabla \times \mathbf{A})} {\partial t}= |
|||
Электродинамические поля — это электрические поля, которые меняются со временем, например, когда заряды находятся в движении. |
|||
-\frac{\partial \mathbf{B}} {\partial t}</math> |
|||
В этом случае электрическое и магнитное поля связаны, причём магнитное поле <math>\mathbf{B}</math> — в соответствии с [[Теорема о циркуляции магнитного поля|законом Ампера]], [[Уравнения Максвелла|с учётом уравнения Максвелла]] — определяется из уравнения в виде (слева — дифференциальном, справа — интегральном): |
|||
что a posteriori подтверждает правильность выбранной формы для '''E.''' |
|||
: <math>\nabla \times \left(\frac{\mathbf{B}}{\mu}\right) = \mu_0\left(\mathbf{j} + \varepsilon_0\varepsilon \frac{\partial \mathbf{E}} {\partial t} \right)\qquad\quad |
|||
\oint\limits_\mathbf{l}\frac{\mathbf{B}}{\mu}\cdot d\mathbf{l}=</math> <math>\mu_0\left(I+\varepsilon_0\frac{d}{d t}\int\limits_\mathbf{s}\varepsilon\mathbf{E}\cdot d\mathbf{s}\right)</math>, |
|||
где <math>\mathbf{j}</math> — [[плотность тока]], <math>\mu_0</math> — [[Магнитная постоянная|магнитная проницаемость вакуума]], <math>\varepsilon_0</math> — [[Электрическая постоянная|диэлектрическая проницаемость вакуума]], <math>\varepsilon</math> и <math>\mu</math> — электрическая и магнитная проницаемости среды (возможно, координатно-зависимые). Интегрирование выполняется по произвольному контуру и по поверхности, натянутой на него, <math>I</math> — полный ток, пронизывающий контур. [[Электрический ток|Электрические токи]] и частная производная электрического поля по времени вносят непосредственный вклад в создание магнитного поля. |
|||
=== Непрерывное и дискретное представление заряда === |
|||
Для записи уравнений электромагнетизма лучше использовать непрерывные функций. Однако иногда заряды удобнее описывать как отдельные точки; например, в некоторых моделях можно описывать [[электрон]]ы как точечные источники, где плотность заряда бесконечна на бесконечно малом участке пространства. |
|||
Кроме того, [[Закон электромагнитной индукции Фарадея|уравнение Максвелла — Фарадея]] утверждает (снова слева — дифференциальный вид, справа — интегральный): |
|||
Заряд <math>q</math> расположенный в <math>\mathbf{r_0}</math> математически можно описать как плотность заряда <math>\rho(\mathbf{r})=q\delta(\mathbf{r-r_0})</math>, где используется [[Дельта-функция|дельта-функция Дирака]] (в трех измерениях). И наоборот, непрерывное распределение заряда можно аппроксимировать множеством небольших точечных зарядов. |
|||
: <math>\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}} {\partial t}\qquad\quad \oint\limits_\mathbf{l}\mathbf{E}\cdot d\mathbf{l}=</math> <math>-\frac{d}{d t}\int\limits_\mathbf{s}\mathbf{B}\cdot d\mathbf{s}</math>. |
|||
Сила, испытываемая пробным зарядом в электромагнитном (совокупно электрическом плюс магнитном) поле, а общем случае определяется [[Сила Лоренца|формулой Лоренца]] |
|||
== Электростатические поля == |
|||
: <math>\mathbf{F} = q\mathbf{E} + q\left[\mathbf{v} \times \mathbf{B}\right]</math>; |
|||
{{main|Электростатическое поле}} |
|||
[[Файл:VFPt_charges_plus_minus_thumb.svg|справа|мини|220x220пкс| Изображение электрического поля, окружающего положительный (красный) и отрицательный (синий) заряды]] |
|||
Электростатические поля — это электрические поля, которые не меняются со временем, что происходит, когда заряды и токи неподвижны. В этом случае [[закон Кулона]] полностью описывает электрическое поле.<ref>Purcell, pp. 5-7.</ref> |
|||
в [[Электростатика|электростатике]] или [[Магнитостатика|магнитостатике]] в этой формуле остаётся, соответственно, только первое или только второе слагаемое. |
|||
=== Параллели между электростатическим и гравитационным полями === |
|||
Закон Кулона, описывающий взаимодействие электрических зарядов: |
|||
=== Однородные поля === |
|||
: <math> |
|||
Однородное поле — это поле, не зависящее от координат. Приблизительно такое электрическое поле возникает, если разместить две проводящие [[Электрический конденсатор|пластины]] параллельно друг другу и поддерживать [[Электрическое напряжение|между ними напряжение]] (разность потенциалов), хотя из-за граничных эффектов (около краёв) электрическое поле искажается. |
|||
\mathbf{F}=q\left(\frac{Q}{4\pi\varepsilon_0}\frac{\mathbf{\hat{r}}}{|\mathbf{r}|^2}\right)=q\mathbf{E} |
|||
</math> |
|||
В предположении бесконечных плоскостей величина электрического поля в пространстве между ними составляет <math> E = - \Delta V/d</math>, где Δ''V'' — [[Электрическое напряжение|разность потенциалов]] между пластинами, а ''d'' — расстояние, разделяющее пластины. Отрицательный знак возникает, когда положительные заряды отталкиваются, поэтому на положительный заряд будет действовать сила от положительно заряженной пластины в направлении, противоположном тому, в котором увеличивается напряжение. |
|||
похож на [[Классическая теория тяготения Ньютона|закон всемирного тяготения Ньютона]] : |
|||
Однородное поле может зависеть от времени <math>t</math>, синхронно изменяясь во всех точках рассматриваемой области (в приведённом примере — если Δ''V'' = Δ''V''(<math>t</math>)), но чаще однородное поле рассматривается в задачах электростатики. |
|||
: <math> |
|||
\mathbf{F}=m\left(-GM\frac{\mathbf{\hat{r}}}{|\mathbf{r}|^2}\right)=m\mathbf{g} |
|||
</math> |
|||
В микро- и нано- приложениях, например относящихся к полупроводникам, типичная величина электрического поля составляет порядка {{Val|e=6|u=В⋅м<sup>−1</sup>}}, которое достигается за счет приложения напряжения порядка 1 вольта между проводниками, расположенными на расстоянии 1 мкм друг от друга. |
|||
(где <math>\mathbf{\hat{r}}=\mathbf{r/|r|}</math> — единичный вектор), что предполагает сходство между электрическим полем '''E''' и гравитационным полем '''g''' или связанными с ними потенциалами. Масса иногда называется «гравитационным зарядом».<ref>{{Cite journal|author=Salam|first=Abdus|title=Quarks and leptons come out to play|journal=New Scientist|date=16 December 1976|volume=72|url=https://books.google.com/books?id=WIbyn2jxGhoC&pg=PA652}}</ref> |
|||
== Электрическое поле в среде == |
|||
И электростатические и гравитационные силы являются [[Центральная сила|центральными]], [[Консервативные силы|консервативными]] и подчиняются [[Закон обратных квадратов|закону обратных квадратов]]. |
|||
=== Реакция разных сред на поле === |
|||
=== Однородные поля === |
|||
[[Файл:VFPt_capacitor-square-plate.svg|справа|мини|220x220пкс| Изображение линий электрического поля между двумя параллельными [[Проводник (физика)|проводящими]] пластинами конечного размера (известного как [[Электрический конденсатор|конденсатор с параллельными пластинами]]). В середине между пластинвми, и вдали от краев, электрическое поле почти однородно.]] |
|||
Однородное поле — это поле, в котором электрическое поле постоянно в каждой точке. Это можно приблизительно представить, разместив две проводящие [[Электрический конденсатор|пластины]] параллельно друг другу и поддерживая [[Электрическое напряжение|между ними напряжение]] (разность потенциалов), но из-за граничных эффектов (около края плоскостей) электрическое поле искажается. В предположении бесконечных плоскостей величина электрического поля ''E'' равна: |
|||
: <math> E = - \frac{\Delta V}{d}</math> |
|||
где Δ ''V'' — [[Электрическое напряжение|разность потенциалов]] между пластинами, а ''d'' — расстояние, разделяющее пластины. Отрицательный знак возникает, когда положительные заряды отталкиваются, поэтому на положительный заряд будет действовать сила от положительно заряженной пластины в направлении, противоположном тому, в котором увеличивается напряжение. В микро- и нано-приложениях, например, относящихся к полупроводникам, типичная величина электрического поля составляет порядка {{Val|e=6|u=V⋅m<sup>−1</sup>}}, которое достигается за счет приложения напряжения порядка 1 вольта между проводниками, расположенными на расстоянии 1 мкм друг от друга. |
|||
== Электродинамические поля == |
|||
[[Файл:Electrostatic_induction.svg|мини| Электрическое поле ''(линии со стрелками)'' заряда ''<span style="color:red;">(+)</span>'' индуцирует поверхностные заряды ''(<span style="color:red;">красные</span> и <span style="color:blue;">синие</span> области)'' на металлических объектах из-за [[Электростатическая индукция|электростатической индукции]].]] |
[[Файл:Electrostatic_induction.svg|мини| Электрическое поле ''(линии со стрелками)'' заряда ''<span style="color:red;">(+)</span>'' индуцирует поверхностные заряды ''(<span style="color:red;">красные</span> и <span style="color:blue;">синие</span> области)'' на металлических объектах из-за [[Электростатическая индукция|электростатической индукции]].]] |
||
Реакция материальной среды на наложение электрического поля зависит от того, насколько свободными являются электрические заряды (ионы, электроны, дырки) этой среды. Если они могут свободно перемещаться, то на поверхности возникает индуцированный заряд, распределённый таким образом, чтобы воспрепятствовать проникновению поля вглубь образца — такой вариант реакции (см. рис.) типичен для проводящих металлических материалов. Если заряды свободно перемещаться не могут, то происходит их локальное, на атомных масштабах, смещение, в результате чего в местах неоднородностей материала и на границах появляется связанный заряд — такой отклик характерен для диэлектриков (см. в статье [[Диэлектрическая проницаемость]]). В [[Полупроводник|полупроводниках]] возможна «смешанная» реакция. Перемещённые электрические заряды сами становятся источниками поля, искажая картину поля во всём пространстве. |
|||
Электродинамические поля — это электрические поля, которые меняются со временем, например, когда заряды находятся в движении. |
|||
Отклик среды на электрическое поле зависит от скорости изменения поля (заряды могут не успевать смещаться) и может сильно различаться в зависимости от [[Частота|частоты]]. Для диэлектриков эта деталь характеризуется частотной зависимостью проницаемости. |
|||
В этом случае магнитное поле создается в соответствии с [[Теорема о циркуляции магнитного поля|законом Ампера]] ([[Уравнения Максвелла|с учётом уравнений Максвелла]]), который, наряду с другими уравнениями Максвелла, определяет магнитное поле <math>\mathbf{B}</math> в виде |
|||
=== Материальное соотношение === |
|||
: <math>\nabla \times \mathbf{B} = \mu_0\left(\mathbf{J} + \varepsilon_0 \frac{\partial \mathbf{E}} {\partial t} \right) ,</math> |
|||
В присутствии вещества понятие электрического поля может быть расширено до трех векторных полей:<ref name="auto">Electromagnetism (2nd Edition), I.S. Grant, W.R. Phillips, Manchester Physics, John Wiley & Sons, 2008, {{ISBN|978-0-471-92712-9}}</ref> |
|||
: <math>\mathbf{D}=\varepsilon_0\mathbf{E}+\mathbf{P}\!</math>, |
|||
где <math>\mathbf{J}</math> — [[плотность тока]], <math>\mu_0</math> — [[Магнитная постоянная|магнитная проницаемость вакуума]], а <math>\varepsilon_0</math> — [[Электрическая постоянная|диэлектрическая проницаемость вакуума]]. [[Электрический ток|Электрические токи]] (заряды, движущиеся равномерно) и частная производная электрического поля по времени вносят непосредственный вклад в создание магнитного поля. |
|||
где '''P''' — [[поляризованность]] диэлектрика — объемная плотность [[Электрический дипольный момент|электрических дипольных моментов]], а '''D''' — поле [[Электрическая индукция|электрической индукции]]. Поскольку '''E''' и '''P''' определяются отдельно, это уравнение можно использовать для определения '''D.''' Физическая интерпретация '''D''' не так ясна, как '''E''' (фактически поле, приложенное к материалу) или '''P''' (индуцированное поле из-за электрических диполей в материале), но всё же служит удобным математическим упрощением, поскольку уравнения Максвелла можно упростить в терминах [[Уравнения Максвелла|свободных зарядов и токов]]. |
|||
Кроме того, [[Закон электромагнитной индукции Фарадея|уравнение Максвелла — Фарадея]] утверждает |
|||
Поля '''E''' и '''D''' [[Диэлектрическая проницаемость|связаны посредством диэлектрической проницаемости]] материала ''ε'' .<ref>''Electricity and Modern Physics (2nd Edition)'', G.A.G. Bennet, Edward Arnold (UK), 1974, {{ISBN|0-7131-2459-8}}</ref> |
|||
: <math>\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}} {\partial t}.</math> |
|||
Для линейных, однородных, [[Изотропия|изотропных]] материалов '''E''' и '''D''' пропорциональны и постоянны во всём объёме, без зависимости от координат |
|||
Выписанные выше два из [[Уравнения Максвелла|четырех уравнений Максвелла]] тесно связывают электрическое и магнитное поля, в результате чего [[Электромагнитное поле|возникает электромагнитное поле]]. |
|||
: <math>\mathbf{D}=\varepsilon_0\varepsilon\mathbf{E}</math>. |
|||
Для неоднородных материалов существует координатная зависимость<ref>{{Cite book|author=Landau Lev Davidovich, Lifshitz Evgeny M.|url=https://books.google.com/books?id=XX0xxgEACAAJ|title=Electrodynamics of Continuous Media|date=1963|series=[[Course of Theoretical Physics]]|volume=8|publisher=Pergamon|isbn=978-0-7581-6499-5|page=285|language=en|quote=In Maxwell's equations… ''ε'' is a function of the co-ordinates.}}</ref> |
|||
Сила, испытываемая пробным зарядом в электромагнитном поле, а общем случае определяется [[Сила Лоренца|формулой Лоренца]] |
|||
: <math>\mathbf{D(r)}=\varepsilon_0\varepsilon (\mathbf{r})\mathbf{E(r)}</math>. |
|||
Для анизотропных материалов '''поля E''' и '''D''' не параллельны, и поэтому '''E''' и '''D''' связаны посредством [[Диэлектрическая проницаемость|тензора диэлектрической проницаемости]] [[Тензорное поле|(поле тензора]] 2-го ранга) в компонентной форме: |
|||
: <math>\mathbf{F} = q\mathbf{E} + q\mathbf{v} \times \mathbf{B}</math>; |
|||
: <math>D_i=\varepsilon_0\varepsilon_{ij}E_j</math>. |
|||
Для нелинейных сред '''E''' и '''D''' непропорциональны. Материалы могут иметь различную степень линейности, однородности и изотропии. |
|||
в [[Электростатика|электростатике]] или [[Магнитостатика|магнитостатике]] в этой формуле остаётся, соответственно, только первое или только второе слагаемое. |
|||
== Энергия электрического поля == |
== Энергия электрического поля == |
||
{{Энергия}} |
{{Энергия}} |
||
{{main|Электромагнитная энергия}} |
{{main|Электромагнитная энергия}} |
||
Полная энергия на единицу объёма, запасённая [[Электромагнитное поле|электромагнитным полем |
Полная энергия на единицу объёма, запасённая [[Электромагнитное поле|электромагнитным полем]] в линейной среде, равняется<ref>Introduction to Electrodynamics (3rd Edition), D.J. Griffiths, Pearson Education, Dorling Kindersley, 2007, {{ISBN|81-7758-293-3}}</ref> |
||
: <math> u_{EM} = \frac{\varepsilon_0\varepsilon}{2} |\mathbf{E}|^2 + \frac{1}{2\mu_0\mu} |\mathbf{B}|^2 </math>. |
|||
: <math> u_{EM} = \frac{\varepsilon}{2} |\mathbf{E}|^2 + \frac{1}{2\mu} |\mathbf{B}|^2 </math> |
|||
где ''ε'' — [[диэлектрическая проницаемость]] среды, в которой существует поле, <math>\mu</math> её [[магнитная проницаемость]], а '''E''' и '''B''' — векторы электрического и магнитного полей. |
|||
Поскольку '''поля E''' и '''B''' связаны, то было бы ошибочным разделять это выражение на «электрические» и «магнитные» вклады. Однако в стационарном случае поля больше не связаны (см. [[Уравнения Максвелла]]). В этом случае имеет смысл вычислить электростатическую энергию в единице объёма |
|||
Поскольку поля '''E''' и '''B''' связаны, было бы искусственным разделять это выражение на «электрический» и «магнитный» вклады. Однако в стационарном случае поля не связаны. В этом случае имеет смысл вычислить электростатическую энергию в единице объёма |
|||
: <math> u_{ES} = \frac{1}{2} \varepsilon |\mathbf{E}|^2 \, ,</math> |
|||
: <math> u_{E} = \frac{1}{2} \varepsilon_0\varepsilon |\mathbf{E}|^2 \, </math>. |
|||
Таким образом, полная энергия ''U,'' запасённая в электрическом поле в данном объёме ''V,'' равна |
Таким образом, полная энергия ''U,'' запасённая в электрическом поле в данном объёме ''V,'' равна |
||
: <math> U_{E} = \frac{1}{2} \varepsilon_0\varepsilon \int_{V} |\mathbf{E}|^2 \, \mathrm{d}V \,</math>. |
|||
С другой стороны, электростатическая энергия может быть вычислена через плотность заряда <math> \rho </math> и электрический потенциал <math> \varphi </math> путём интегрирования по объёму системы: |
|||
: <math> U_{ES} = \frac{1}{2} \varepsilon \int_{V} |\mathbf{E}|^2 \, \mathrm{d}V \, .</math> |
|||
: <math> U_{E} = \int_{V} \rho \varphi \, \mathrm{d}V \, .</math> |
|||
С другой стороны, электростатическая энергия может быть вычислена через плотность заряда <math> \rho </math> и электрический потенциал <math> \Phi </math> путём интегрирования по объёму системы: |
|||
Равенство двух выражений для электростатической энергии, одно из которых зависит от электрического поля '''E''', а другое от потенциала <math> \varphi </math>, доказывается интегральной теоремой об энергии поля, при этом интегрирование делается по всему бесконечному объёму.<ref>Fedosin S.G. [http://dergipark.org.tr/gujs/issue/45480/435567 The Integral Theorem of the Field Energy.] Gazi University Journal of Science. Vol. 32, No. 2, pp. 686-703 (2019). http://dx.doi.org/10.5281/zenodo.3252783. // [http://sergf.ru/tf.htm Интегральная теорема энергии поля].</ref> |
|||
: <math> U_{ES} = \int_{V} \rho \Phi \, \mathrm{d}V \, .</math> |
|||
Равенство двух выражений для электростатической энергии, одно из которых зависит от электрического поля '''E''', а другое от электрического потенциала <math> \Phi </math>, доказывается интегральной теоремой энергии поля, при этом интегрирование делается по всему бесконечному объёму. <ref> Fedosin S.G. [http://dergipark.org.tr/gujs/issue/45480/435567 The Integral Theorem of the Field Energy.] Gazi University Journal of Science. Vol. 32, No. 2, pp. 686-703 (2019). http://dx.doi.org/10.5281/zenodo.3252783. // [http://sergf.ru/tf.htm Интегральная теорема энергии поля].</ref> |
|||
== Поле электрической индукции == |
|||
=== Полное уравнение векторных полей === |
|||
В присутствии вещества полезно расширить понятие электрического поля до трех векторных полей:<ref name="auto">Electromagnetism (2nd Edition), I.S. Grant, W.R. Phillips, Manchester Physics, John Wiley & Sons, 2008, {{ISBN|978-0-471-92712-9}}</ref> |
|||
: <math>\mathbf{D}=\varepsilon_0\mathbf{E}+\mathbf{P}\!</math>, |
|||
где '''P''' — [[Поляризованность]] диэлектрика — объемная плотность [[Электрический дипольный момент|электрических дипольных моментов]], а '''D''' — поле [[Электрическая индукция|электрического индукция]]. Поскольку '''E''' и '''P''' определяются отдельно, это уравнение можно использовать для определения '''D.''' Физическая интерпретация '''D''' не так ясна, как '''E''' (фактически поле, приложенное к материалу) или '''P''' (индуцированное поле из-за электрических диполей в материале), но всё же служит удобным математическим упрощением, поскольку уравнения Максвелла можно упростить в терминах [[Уравнения Максвелла|свободных зарядов и токов]]. |
|||
=== Материальное соотношение === |
|||
Поля '''E''' и '''D''' [[Диэлектрическая проницаемость|связаны посредством диэлектрической проницаемости]] материала ''ε'' .<ref>''Electricity and Modern Physics (2nd Edition)'', G.A.G. Bennet, Edward Arnold (UK), 1974, {{ISBN|0-7131-2459-8}}</ref> |
|||
Для линейных, однородных, [[Изотропия|изотропных]] материалов '''E''' и '''D''' пропорциональны и постоянны во всём объёме, без зависимости от координат |
|||
: <math>\mathbf{D}=\varepsilon\mathbf{E}</math> |
|||
Для неоднородных материалов существует координатная зависимость<ref>{{Cite book|author=Landau Lev Davidovich, Lifshitz Evgeny M.|url=https://books.google.com/books?id=XX0xxgEACAAJ|title=Electrodynamics of Continuous Media|date=1963|series=[[Course of Theoretical Physics]]|volume=8|publisher=Pergamon|isbn=978-0-7581-6499-5|page=285|language=en|quote=In Maxwell's equations… ''ε'' is a function of the co-ordinates.}}</ref> |
|||
: <math>\mathbf{D(r)}=\varepsilon (\mathbf{r})\mathbf{E(r)}</math> |
|||
Для анизотропных материалов '''поля E''' и '''D''' не параллельны, и поэтому '''E''' и '''D''' связаны посредством [[Диэлектрическая проницаемость|тензора диэлектрической проницаемости]] [[Тензорное поле|(поле тензора]] 2-го ранга) в компонентной форме: |
|||
: <math>D_i=\varepsilon_{ij}E_j</math> |
|||
Для нелинейных сред '''E''' и '''D''' непропорциональны. Материалы могут иметь различную степень линейности, однородности и изотропии. |
|||
== Наблюдение электрического поля в быту == |
== Наблюдение электрического поля в быту == |
||
Для того, чтобы создать электрическое поле, необходимо создать [[Электризация|электрический заряд]]. |
Для того, чтобы создать электрическое поле, необходимо создать [[Электризация|электрический заряд]]. Если натереть какой-либо диэлектрик о шерсть или что-нибудь подобное, например, пластиковую ручку о собственные чистые волосы, то на диэлектрике (ручке) создастся заряд, а вокруг — электрическое поле. Заряженная ручка будет притягивать к себе мелкие обрывки бумаги. Если натирать о шерсть предмет большей ширины, сажем, резиновую ленту, то в темноте можно будет видеть мелкие искры, возникающие вследствие [[Электрический разряд|электрических разрядов]]. |
||
Электрическое поле часто возникает возле телевизионного экрана (относится к телевизорам с [[Кинескоп|ЭЛТ]]) при включении или выключении телеприёмника. Это поле можно почувствовать по его действию на волоски на руках или лице. |
Электрическое поле часто возникает возле телевизионного экрана (относится к телевизорам с [[Кинескоп|ЭЛТ]]) при включении или выключении телеприёмника. Это поле можно почувствовать по его действию на волоски на руках или лице. |
||
== Методы расчета электрического поля == |
|||
Расчёты электрического поля можно проводить аналитическими<ref>''Гринберг Г. А.'' Избранные вопросы математической теории электрических и магнитных явлений. — М.: АН СССР, 1948. — 727 с.</ref><ref>''Миролюбов Н. Н., Костенко М. В., Левинштейн М. Л.'' Методы расчета электростатических полей. — М.: Высшая школа, 1963. — 416 с.</ref><ref>''Смайт В.'' Электростатика и электродинамика. — М.: ИЛ, 1954. — 604 с.</ref> или численными методами<ref name = "Kole">''Колечицкий Е. С.'' Расчет электрических полей устройств высокого напряжения. — М.: Энергоатомиздат, 1983. — 168 с.</ref>. Аналитические методы удаётся применить лишь в простейших случаях, на практике в основном используются численные методы. Численные методы включают в себя: метод сеток или [[метод конечных разностей]]; вариационные методы; [[метод конечных элементов]]; метод интегральных уравнений; метод эквивалентных зарядов<ref name = "Kole"></ref>. |
|||
== Электрическое поле Земли == |
== Электрическое поле Земли == |
||
{{main|Электрическое поле Земли}} |
{{main|Электрическое поле Земли}} |
||
Земля имеет отрицательный заряд около 600000 Кл. В свою очередь, ионосфера Земли имеет положительный заряд. Поэтому, вся атмосфера Земли до высоты примерно в 50 |
Земля имеет отрицательный заряд около 600000 Кл. В свою очередь, ионосфера Земли имеет положительный заряд. Поэтому, вся атмосфера Земли до высоты примерно в 50 км заполнена электрическим полем, которое можно приближенно считать однородным<ref name="caltech">[https://www.feynmanlectures.caltech.edu/II_09.html Electricity in the Atmosphere]{{ref-en}}</ref>. Напряженность этого поля составляет от 100 до 300 В/м у поверхности. Мы не чувствуем этой разности потенциалов, поскольку человеческое тело является проводником, поэтому заряд частично переходит с Земли в него. Благодаря этому тело образует вместе с поверхностью Земли единую эквипотенциальную поверхность (то есть разность потенциалов между произвольной точкой на высоте 2 м и поверхностью Земли — около 200 вольт, однако разность потенциалов между головой человека и поверхностью Земли, на которой она стоит — близка к нулю). |
||
Общая разность потенциалов между Землёй и ионосферой составляет 400000 вольт<ref name="caltech"></ref>. |
Общая разность потенциалов между Землёй и ионосферой составляет 400000 вольт<ref name="caltech"></ref>. |
||
Электрическое поле Земли влияет на движение заряженных частиц в атмосфере. Положительно заряженные частицы движутся в ней вниз, а отрицательно заряженные |
Электрическое поле Земли влияет на движение заряженных частиц в атмосфере. Положительно заряженные частицы движутся в ней вниз, а отрицательно заряженные — вверх. Заряженные частицы постоянно образуются в атмосфере под действием космических лучей, благодаря чему в ней поддерживается постоянный ток с силой 10<sup>−12</sup> ампер на каждый квадратный метр<ref name="caltech"></ref>. |
||
== Безопасность в зоне |
== Безопасность в зоне электрического поля == |
||
Электрическое поле возникает при наличии напряжения на токоведущих частях [[Электроустановка|электроустановок]]. |
Электрическое поле возникает при наличии напряжения на токоведущих частях [[Электроустановка|электроустановок]]. |
||
Пространство, в котором [[Напряжённость электрического поля|напряжённость электрического поля]] равна 5 кВ/м и больше, принято называть опасной зоной или зоной влияния. Приближённо можно считать, что эта зона лежит в пределах круга с центром в точке расположения ближайшей токоведущей части, находящейся под напряжением, и радиусом R = 20 м для электроустановок 400—500 кВ и R = 30 м для электроустановок 750 кВ. |
Пространство, в котором [[Напряжённость электрического поля|напряжённость электрического поля]] равна 5 кВ/м и больше, принято называть опасной зоной или зоной влияния. Приближённо можно считать, что эта зона лежит в пределах круга с центром в точке расположения ближайшей токоведущей части, находящейся под напряжением, и радиусом R = 20 м для электроустановок 400—500 кВ и R = 30 м для электроустановок 750 кВ. |
||
В ОРУ 110 кВ и выше и на ВЛ 330 кВ и выше при выполнении работ в зоне влияния электрического поля напряжённостью свыше 5 кВ/м необходимо ограничивать длительность пребывания людей согласно требованиям ГОСТ 12.1.002 или применять средства защиты от воздействия электрического поля (далее — средства защиты). |
В [[Распределительное устройство#Открытое распределительное устройство (ОРУ)|ОРУ]] 110 кВ и выше и на [[Линия электропередачи#Воздушные линии электропередачи|ВЛ]] 330 кВ и выше при выполнении работ в зоне влияния электрического поля напряжённостью свыше 5 кВ/м необходимо ограничивать длительность пребывания людей согласно требованиям ГОСТ 12.1.002 или применять средства защиты от воздействия электрического поля (далее — средства защиты). |
||
{{начало скрытого блока|ограничения на время пребывания в зоне влияния}} |
|||
При напряжённости электрического поля до 5 кВ/м длительность пребывания в нём не ограничивается. |
При напряжённости электрического поля до 5 кВ/м длительность пребывания в нём не ограничивается. |
||
Допустимая продолжительность Т (в часах) пребывания в электрическом поле напряжённостью в от 5 до 20 кВ/м включительно вычисляется по формуле: |
|||
<math>T = 50/E - 2</math> часов, |
|||
где Е — напряжённость (выраженная в кВ/м) действующего электрического поля в контролируемой зоне. |
|||
Продолжительность работы в электрическом поле напряжённостью от 20 до 25 кВ/м не должна превышать 10 мин. При напряженности свыше 25 кВ/м следует применять средства защиты, позволяющие работать полный рабочий день. |
Продолжительность работы в электрическом поле напряжённостью от 20 до 25 кВ/м не должна превышать 10 мин. При напряженности свыше 25 кВ/м следует применять средства защиты, позволяющие работать полный рабочий день. |
||
Вышеизложенные требования действительны при условии исключения возможности воздействия на работников электрических разрядов. |
|||
Допустимая продолжительность Т (в часах) пребывания в электрическом поле напряжённостью в от 5 до 20 кВ/м включительно вычисляется по формуле: |
|||
Допустимая продолжительность пребывания в зоне воздействия электрического поля без средств защиты может быть реализована единоразово или с перерывами в течение рабочего дня. В течение остального времени следует применять средства защиты или находиться в электрическом поле напряженностью до 5 кВ/м. |
|||
<math>T = 50/E - 2</math> , ч. |
|||
В различных точках пространства вблизи электроустановок напряжённость электрического поля имеет разные значения и зависит от ряда факторов: номинального напряжения, расстояния (по высоте и горизонтали) рассматриваемой точки от токоведущих частей и др. |
|||
где Е — напряжённость (выраженная в кВ/м) действующего электрического поля в контролируемой зоне. |
|||
Продолжительность пребывания человека в контролируемой зоне устанавливается с учётом наибольшего значения измеренной напряжённости. |
|||
Вышестоящие требования действительны при условии исключения возможности воздействия на работников электрических разрядов. |
|||
{{конец скрытого блока}} |
|||
Наряду с биологическим действием электрическое поле обусловливает возникновение разрядов между человеком и металлическим предметом, имеющим иной по сравнению с телом человека потенциал. Если человек стоит непосредственно на земле или на токопроводящем заземлённом основании, то потенциал его тела практически равен нулю, а если он изолирован от земли, то тело оказывается под некоторым потенциалом, достигающим иногда нескольких киловольт. |
Наряду с биологическим действием электрическое поле обусловливает возникновение разрядов между человеком и металлическим предметом, имеющим иной по сравнению с телом человека потенциал. Если человек стоит непосредственно на земле или на токопроводящем заземлённом основании, то потенциал его тела практически равен нулю, а если он изолирован от земли, то тело оказывается под некоторым потенциалом, достигающим иногда нескольких киловольт. |
||
{{начало скрытого блока|подробнее об электрических разрядах}} |
|||
Очевидно, что прикосновение человека, изолированного от земли, к заземленному металлическому предмету, равно как и прикосновение заземлённого человека к металлическому предмету, изолированному от земли, сопровождается прохождением через человека в землю разрядного тока, который может вызывать болезненные ощущения, особенно в первый момент. Часто прикосновение сопровождается искровым разрядом. В случае прикосновения к изолированному от земли металлическому предмету большой протяжённости (трубопровод, проволочная ограда на деревянных стойках и т. п. или большого размера металлическая крыша деревянного здания и пр.) сила тока, проходящего через человека, может достигать значений, опасных для жизни. |
Очевидно, что прикосновение человека, изолированного от земли, к заземленному металлическому предмету, равно как и прикосновение заземлённого человека к металлическому предмету, изолированному от земли, сопровождается прохождением через человека в землю разрядного тока, который может вызывать болезненные ощущения, особенно в первый момент. Часто прикосновение сопровождается искровым разрядом. В случае прикосновения к изолированному от земли металлическому предмету большой протяжённости (трубопровод, проволочная ограда на деревянных стойках и т. п. или большого размера металлическая крыша деревянного здания и пр.) сила тока, проходящего через человека, может достигать значений, опасных для жизни. |
||
Допустимое значение тока, длительно проходящего через человека и обусловленного воздействием электрического поля электроустановок сверхвысокого напряжения, составляет примерно 50—60 мкА, что соответствует напряжённости электрического поля на высоте роста человека примерно 5 кВ/м. Если при электрических разрядах, возникающих в момент прикосновения человека к металлической конструкции, имеющей иной, чем человек, потенциал, установившийся ток не превышает 50— 60 мкА, то человек, как правило, не испытывает болевых ощущений. Поэтому это значение тока принято в качестве нормативного (допустимого). |
Допустимое значение тока, длительно проходящего через человека и обусловленного воздействием электрического поля электроустановок сверхвысокого напряжения, составляет примерно 50—60 мкА, что соответствует напряжённости электрического поля на высоте роста человека примерно 5 кВ/м. Если при электрических разрядах, возникающих в момент прикосновения человека к металлической конструкции, имеющей иной, чем человек, потенциал, установившийся ток не превышает 50— 60 мкА, то человек, как правило, не испытывает болевых ощущений. Поэтому это значение тока принято в качестве нормативного (допустимого). |
||
{{конец скрытого блока}} |
|||
Допустимая продолжительность пребывания в зоне воздействия электрического поля без средств защиты может быть реализована единоразово или с перерывами в течение рабочего дня. В течение остального времени следует применять средства защиты или находиться в электрическом поле напряженностью до 5 кВ/м. |
|||
В различных точках пространства вблизи электроустановок напряжённость электрического поля имеет разные значения и зависит от ряда факторов: номинального напряжения, расстояния (по высоте и горизонтали) рассматриваемой точки от токоведущих частей и др. |
|||
Продолжительность пребывания человека в контролируемой зоне устанавливается с учётом наибольшего значения измеренной напряжённости. |
|||
Основными средствами коллективной защиты от воздействия электрического поля промышленной частоты являются стационарные и переносные разновидности экранирующих устройств. |
Основными средствами коллективной защиты от воздействия электрического поля промышленной частоты являются стационарные и переносные разновидности экранирующих устройств. |
||
В заземлённых кабинах и кузовах машин, механизмов, передвижных мастерских и лабораторий, в зданиях из железобетона, в кирпичных зданиях с железобетонным перекрытием, металлическим каркасом или заземлённой металлической кровлей электрическое поле отсутствует и применения средств защиты не требуется. |
|||
Переносные и передвижные экранирующие устройства необходимо заземлять на месте их установки с помощью присоединения к заземляющему устройству или металлическим конструкциям, которые соединены с заземляющим устройством, гибким медным проводником сечением не менее 4 мм<sup>2</sup>. |
Переносные и передвижные экранирующие устройства необходимо заземлять на месте их установки с помощью присоединения к заземляющему устройству или металлическим конструкциям, которые соединены с заземляющим устройством, гибким медным проводником сечением не менее 4 мм<sup>2</sup>. |
||
{{начало скрытого блока|подробнее о средствах защиты и заземлении}} |
|||
Съёмные экранирующие устройства должны иметь гальваническое соединение с механизмами, на которых они установлены. Для заземления машин и механизмов дополнительного заземления съёмных экранирующих устройств не требуется. |
Съёмные экранирующие устройства должны иметь гальваническое соединение с механизмами, на которых они установлены. Для заземления машин и механизмов дополнительного заземления съёмных экранирующих устройств не требуется. |
||
| Строка 284: | Строка 237: | ||
При подъёме на оборудование и конструкции, расположенные в зоне влияния электрического поля, следует применять средства защиты независимо от значения напряжённости электрического поля и продолжительности работы в нём. В случае поднятия с помощью телескопической вышки или гидроподъёмника их корзины (люльки) следует оборудовать экраном или применять экранирующие комплекты. |
При подъёме на оборудование и конструкции, расположенные в зоне влияния электрического поля, следует применять средства защиты независимо от значения напряжённости электрического поля и продолжительности работы в нём. В случае поднятия с помощью телескопической вышки или гидроподъёмника их корзины (люльки) следует оборудовать экраном или применять экранирующие комплекты. |
||
{{конец скрытого блока}} |
|||
В заземлённых кабинах и кузовах машин, механизмов, передвижных мастерских и лабораторий, в зданиях из железобетона, в кирпичных зданиях с железобетонным перекрытием, металлическим каркасом или заземлённой металлической кровлей электрическое поле отсутствует и применения средств защиты не требуется. |
|||
== Примечания == |
== Примечания == |
||
| Строка 291: | Строка 246: | ||
* {{Cite book|author1=Purcell, Edward|author2=Morin, David|title=ELECTRICITY AND MAGNETISM|edition=3rd|publisher=Cambridge University Press, New York|year=2013|isbn=978-1-107-01402-2}} |
* {{Cite book|author1=Purcell, Edward|author2=Morin, David|title=ELECTRICITY AND MAGNETISM|edition=3rd|publisher=Cambridge University Press, New York|year=2013|isbn=978-1-107-01402-2}} |
||
* {{Cite book|author1=Browne, Michael|title=PHYSICS FOR ENGINEERING AND SCIENCE|edition=2nd|publisher=McGraw-Hill, Schaum, New York|year=2011|isbn=978-0-07-161399-6}} |
* {{Cite book|author1=Browne, Michael|title=PHYSICS FOR ENGINEERING AND SCIENCE|edition=2nd|publisher=McGraw-Hill, Schaum, New York|year=2011|isbn=978-0-07-161399-6}} |
||
[[Категория:Электромагнетизм]] |
[[Категория:Электромагнетизм]] |
||
[[Категория:Физические величины]] |
[[Категория:Физические величины]] |
||
Версия от 20:28, 10 марта 2023
Электри́ческое по́ле — вид материи, который окружает каждый электрический заряд, а также возникает при наличии изменяющегося во времени магнитного поля, и оказывает силовое воздействие на все покоящиеся заряды, притягивая или отталкивая их[1][2].
Электрическое поле математически определяется как векторное поле, которое связывает с каждой точкой в пространстве силу (электростатическую, или кулоновскую) на единицу заряда, приложенную к бесконечно малому положительному пробному заряду, покоящемуся в этой точке[3][4][5]. Величина указанного векторного поля называется его напряжённостью (обозначение: ). В системе СИ единица измерения напряжённости электрического поля: вольт на метр (В/м) или, что то же самое, ньютон на кулон (Н/Кл).
Электрические и магнитные поля рассматриваются как проявления более общей физической реальности — электромагнитного поля, ответственного за одно из фундаментальных взаимодействий природы (наряду с гравитационным, сильным и слабым). Частным случаем электрического поля является электростатическое.
Электрические поля важны во многих областях физики и используются практически в электротехнике. Например, в атомной физике и химии электрическое поле — это сила удерживающая атомное ядро и электроны вместе в атомах. Эта сила отвечает за химические связи между атомами, в результате которых образуются молекулы. Другие использования электрических полей включают обнаружение движения посредством ёмкостных методов и растущее число диагностических и терапевтических медицинских применений.
Качественное описание
Под электрическим полем одновременно понимаются
- вид материи, оказывающий силовое воздействие на электрические заряды, в том числе покоящиеся;
- физическая векторная величина напряжённости электрического поля.
Вторая из указанных трактовок несколько сужает предмет, поскольку напряжённость выступает основной, но не единственно возможной характеристикой данного вида материи (иной вариант характеризации — использование потенциалов).
Регистрация и некоторые свойства
Напряжённость электрического поля определяется в каждой точке пространства как сила (на единицу заряда), которую испытывает исчезающе малый положительный пробный заряд, помещённый в эту точку.[6] :469–70 Поскольку электрическое поле дефинируется через понятие силы, а сила является вектором (то есть имеет и величину, и направление), электрическое поле является векторным полем . :469–70 Векторные поля такого вида иногда называют силовыми полями. Практически, роль регистратора электрического поля может выполнить заряженное тело малых размеров.
В общем случае поле зависит от трёх пространственных координат и времени: .
Электрическое поле, в зависимости от способа его создания (см. ниже), может быть или не быть потенциальным. Электростатическое поле потенциально всегда.
Достаточно часто электрическое поле сосуществует с магнитным полем, причём имеет место взаимопревращение переменных электрического и магнитного полей, например в электромагнитной волне.
Величина поля зависит от выбора системы отсчета, переход от одной инерциальной системы отсчёта к другой осуществляется с помощью преобразований Лоренца, в которых совместно задействуются и электрическая, и магнитная компоненты электромагнитного поля[7]. Электрическое поле инвариантом преобразований Лоренца не является.
За некоторыми исключениями, электрическое поле подчиняется принципу суперпозиции, то есть поле нескольких источников есть сумма полей, создаваемых источниками. Это утверждение может быть проверено эмпирически и соответствует теоретическим моделям (см. ниже).
Способы создания
Электрическое поле может быть создано
- электрическим зарядом;
- переменным во времени магнитным полем.
Закон Кулона гласит, что электрическое поле стационарных зарядов в вакууме или однородной среде изменяется пропорционально заряду источника и обратно пропорционально квадрату расстояния от источника. Это означает, что при удвоении заряда источника поле удваивается, а если пробный заряд отодвинуть вдвое дальше от источника, то поле в этой точке будет вчетверо слабее его первоначальной силы. Электрическое поле действует между двумя зарядами подобно тому, как гравитационное поле действует между двумя обладающими массой телами, расположенными на каком-то расстоянии, поскольку они оба подчиняются закону обратных квадратов[8].
Закон Фарадея описывает взаимосвязь между изменяющимися во времени магнитным и электрическим полями. Один из способов сформулировать закон Фарадея — ротор электрического поля равен отрицательной частной производной магнитного поля по времени.[9] :327 В отсутствие изменяющегося во времени магнитного поля, электрическое поле потенциально (то есть является безроторным). :24,90–91
Графическое представление

Электрическое поле можно изобразить с помощью набора линий, в каждой своей точке сонаправленных с полем в этой точке. Данная концепция была введена Майклом Фарадеем[10], чей термин «силовые линии» употребляется и ныне. Такое представление полезно тем, что напряжённость электрического поля тем больше, чем гуще проходят линии[11]. Для нестационарного электрического поля картина его силовых линий может быть изображена для выбранного конкретного момента времени.
Обычно к построению силовых линий прибегают для стационарного (электростатического) случая. Силовые линии стационарных зарядов начинаются от положительных зарядов и заканчиваются отрицательными зарядами, они входят во все хорошие проводники под прямым углом, и они никогда не пересекаются и не замыкаются. Линии поля удобны для схематичного представления; но поле фактически пронизывает всё пространство между линиями. Можно нарисовать больше или меньше линий в зависимости от желаемой степени детализации.
Количественное описание
Расчёт электрического поля можно проводить аналитическими[12][13][14] и численными[15] методами. Аналитические методы удаётся применить лишь в простейших случаях, на практике в основном используются численные методы. Они включают: метод сеток или метод конечных разностей; вариационные методы; метод конечных элементов; метод интегральных уравнений; метод эквивалентных зарядов[15]. Ключевые физические формулы представлены ниже.
Базовые уравнения
Основными уравнениями теории электромагнетизма являются уравнения Максвелла. Всего их четыре:
- .
В одно из этих уравнений напряжённость электрического поля входит в явном виде, ещё в два — через вектор электрического смещения . Кроме названных величин, в уравнениях фигурируют индукция и напряжённость магнитного поля. Прочие обозначения: — плотность электрического тока (А/м2), — плотность заряда (Кл/м3), — оператор набла, — время. Это так называемая дифференциальная форма уравнений Максвелла.
Заряд в базовых уравнениях
При работе с уравнениями электромагнетизма лучше использовать непрерывные функции и распределённый заряд. Так, в выписанное выше выражение для электрический заряд входит именно в виде его объёмной плотности. При необходимости, точечный заряд , расположенный в месте с радиус-вектором , математически можно описать как плотность заряда , где используется дельта-функция Дирака (в трех измерениях).
Но уравнения Максвелла могут быть переписаны в интегральной форме, и тогда можно оперировать такими величинами, как заряд или ток (а не плотность заряда, плотность тока). Кроме того, есть физические ситуации, когда традиционно удобнее учитывать «штучность», «дискретность» зарядов: например, в некоторых моделях можно описывать электроны как точечные источники, плотность заряда которых бесконечна на бесконечно малом участке пространства. Также любое непрерывное распределение заряда можно аппроксимировать множеством небольших точечных зарядов.
Принцип суперпозиции
Ввиду линейности уравнений Максвелла, электрические поля удовлетворяют принципу суперпозиции, который гласит, что полное электрическое поле в точке , создаваемое несколькими источниками, есть сумма полей этих источников:
- ,
где индекс k пробегает все источников. В их роли, в простейшем случае, выступают точечные заряды, поле каждого из которых рассчитывается по закону Кулона. В более сложных случаях источниками могут являться распределённые в пространстве заряды или переменные магнитные поля.
Принцип суперпозиции может нарушаться для нелинейных, в первую очередь сегнетоэлектрических, сред, диэлектрическая проницаемость которых зависит от величины поля и от предыстории образца.
Потенциалы электрического поля
Если система статична, так что магнитные поля не меняются во времени, то по закону Фарадея электрическое поле потенциально. В этом случае можно задать электрический потенциал, то есть функцию такую, что .[16] Это аналог гравитационного потенциала. Разница между электрическим потенциалом в двух точках пространства называется разностью потенциалов (или напряжением) между этими двумя точками.
Однако в общем случае электрическое поле нельзя описать независимо от магнитного поля. Учитывая векторный потенциал электромагнитного поля A, определённый как , можно задать электрический потенциал в виде
- ,
где — градиент электрического потенциала и — частная производная от A по времени.
Упоминавшийся выше закон индукции Фарадея можно получить, взяв ротор от этого уравнения[17]: , что a posteriori подтверждает правильность выбранной формы для E.
Уравнения Максвелла могут быть переписаны с использованием скалярного () и векторного () потенциалов, что иногда удобно для вычислений.
Виды электрических полей
Электростатические поля
Электростатические поля — это электрические поля, которые не меняются со временем, существующие, когда заряды неподвижны, а токи, если они есть, постоянны. В этом случае закон Кулона
для силы действия заряда , расположенного в начале координат и создающего поле , на находящийся в точке пробный заряд (или обобщение этого закона для распределённых зарядов) полностью описывает электрическое поле.[18] Однако сфера применения закона Кулона ограничивается задачами для вакуума или сред с фиксированной диэлектрической проницаемостью ; при наличии же неоднородных диэлектриков (с const), используется более сложный математический аппарат, в том числе решение уравнения Пуассона.
Закон Кулона, описывающий взаимодействие электрических зарядов, похож на закон всемирного тяготения Ньютона, что предполагает логическое сходство между электрическим полем E и гравитационным полем g или связанными с ними потенциалами[19].
Электродинамические поля
Электродинамические поля — это электрические поля, которые меняются со временем, например, когда заряды находятся в движении.
В этом случае электрическое и магнитное поля связаны, причём магнитное поле — в соответствии с законом Ампера, с учётом уравнения Максвелла — определяется из уравнения в виде (слева — дифференциальном, справа — интегральном):
- ,
где — плотность тока, — магнитная проницаемость вакуума, — диэлектрическая проницаемость вакуума, и — электрическая и магнитная проницаемости среды (возможно, координатно-зависимые). Интегрирование выполняется по произвольному контуру и по поверхности, натянутой на него, — полный ток, пронизывающий контур. Электрические токи и частная производная электрического поля по времени вносят непосредственный вклад в создание магнитного поля.
Кроме того, уравнение Максвелла — Фарадея утверждает (снова слева — дифференциальный вид, справа — интегральный):
- .
Сила, испытываемая пробным зарядом в электромагнитном (совокупно электрическом плюс магнитном) поле, а общем случае определяется формулой Лоренца
- ;
в электростатике или магнитостатике в этой формуле остаётся, соответственно, только первое или только второе слагаемое.
Однородные поля
Однородное поле — это поле, не зависящее от координат. Приблизительно такое электрическое поле возникает, если разместить две проводящие пластины параллельно друг другу и поддерживать между ними напряжение (разность потенциалов), хотя из-за граничных эффектов (около краёв) электрическое поле искажается.
В предположении бесконечных плоскостей величина электрического поля в пространстве между ними составляет , где ΔV — разность потенциалов между пластинами, а d — расстояние, разделяющее пластины. Отрицательный знак возникает, когда положительные заряды отталкиваются, поэтому на положительный заряд будет действовать сила от положительно заряженной пластины в направлении, противоположном тому, в котором увеличивается напряжение.
Однородное поле может зависеть от времени , синхронно изменяясь во всех точках рассматриваемой области (в приведённом примере — если ΔV = ΔV()), но чаще однородное поле рассматривается в задачах электростатики.
В микро- и нано- приложениях, например относящихся к полупроводникам, типичная величина электрического поля составляет порядка 106 В⋅м−1, которое достигается за счет приложения напряжения порядка 1 вольта между проводниками, расположенными на расстоянии 1 мкм друг от друга.
Электрическое поле в среде
Реакция разных сред на поле
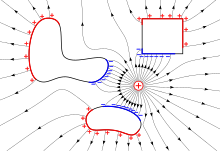
Реакция материальной среды на наложение электрического поля зависит от того, насколько свободными являются электрические заряды (ионы, электроны, дырки) этой среды. Если они могут свободно перемещаться, то на поверхности возникает индуцированный заряд, распределённый таким образом, чтобы воспрепятствовать проникновению поля вглубь образца — такой вариант реакции (см. рис.) типичен для проводящих металлических материалов. Если заряды свободно перемещаться не могут, то происходит их локальное, на атомных масштабах, смещение, в результате чего в местах неоднородностей материала и на границах появляется связанный заряд — такой отклик характерен для диэлектриков (см. в статье Диэлектрическая проницаемость). В полупроводниках возможна «смешанная» реакция. Перемещённые электрические заряды сами становятся источниками поля, искажая картину поля во всём пространстве.
Отклик среды на электрическое поле зависит от скорости изменения поля (заряды могут не успевать смещаться) и может сильно различаться в зависимости от частоты. Для диэлектриков эта деталь характеризуется частотной зависимостью проницаемости.
Материальное соотношение
В присутствии вещества понятие электрического поля может быть расширено до трех векторных полей:[20]
- ,
где P — поляризованность диэлектрика — объемная плотность электрических дипольных моментов, а D — поле электрической индукции. Поскольку E и P определяются отдельно, это уравнение можно использовать для определения D. Физическая интерпретация D не так ясна, как E (фактически поле, приложенное к материалу) или P (индуцированное поле из-за электрических диполей в материале), но всё же служит удобным математическим упрощением, поскольку уравнения Максвелла можно упростить в терминах свободных зарядов и токов.
Поля E и D связаны посредством диэлектрической проницаемости материала ε .[21]
Для линейных, однородных, изотропных материалов E и D пропорциональны и постоянны во всём объёме, без зависимости от координат
- .
Для неоднородных материалов существует координатная зависимость[22]
- .
Для анизотропных материалов поля E и D не параллельны, и поэтому E и D связаны посредством тензора диэлектрической проницаемости (поле тензора 2-го ранга) в компонентной форме:
- .
Для нелинейных сред E и D непропорциональны. Материалы могут иметь различную степень линейности, однородности и изотропии.
Энергия электрического поля
| Виды энергии: | ||
|---|---|---|
| Механическая | Потенциальная Кинетическая | |
| ‹♦› | Внутренняя | |
| Электромагнитная | Электрическая Магнитная | |
| Химическая | ||
| Ядерная | ||
| Гравитационная | ||
| Вакуума | ||
| Гипотетические: | ||
| Тёмная | ||
| См. также: Закон сохранения энергии | ||
Полная энергия на единицу объёма, запасённая электромагнитным полем в линейной среде, равняется[23]
- .
Поскольку поля E и B связаны, было бы искусственным разделять это выражение на «электрический» и «магнитный» вклады. Однако в стационарном случае поля не связаны. В этом случае имеет смысл вычислить электростатическую энергию в единице объёма
- .
Таким образом, полная энергия U, запасённая в электрическом поле в данном объёме V, равна
- .
С другой стороны, электростатическая энергия может быть вычислена через плотность заряда и электрический потенциал путём интегрирования по объёму системы:
Равенство двух выражений для электростатической энергии, одно из которых зависит от электрического поля E, а другое от потенциала , доказывается интегральной теоремой об энергии поля, при этом интегрирование делается по всему бесконечному объёму.[24]
Наблюдение электрического поля в быту
Для того, чтобы создать электрическое поле, необходимо создать электрический заряд. Если натереть какой-либо диэлектрик о шерсть или что-нибудь подобное, например, пластиковую ручку о собственные чистые волосы, то на диэлектрике (ручке) создастся заряд, а вокруг — электрическое поле. Заряженная ручка будет притягивать к себе мелкие обрывки бумаги. Если натирать о шерсть предмет большей ширины, сажем, резиновую ленту, то в темноте можно будет видеть мелкие искры, возникающие вследствие электрических разрядов.
Электрическое поле часто возникает возле телевизионного экрана (относится к телевизорам с ЭЛТ) при включении или выключении телеприёмника. Это поле можно почувствовать по его действию на волоски на руках или лице.
Электрическое поле Земли
Земля имеет отрицательный заряд около 600000 Кл. В свою очередь, ионосфера Земли имеет положительный заряд. Поэтому, вся атмосфера Земли до высоты примерно в 50 км заполнена электрическим полем, которое можно приближенно считать однородным[25]. Напряженность этого поля составляет от 100 до 300 В/м у поверхности. Мы не чувствуем этой разности потенциалов, поскольку человеческое тело является проводником, поэтому заряд частично переходит с Земли в него. Благодаря этому тело образует вместе с поверхностью Земли единую эквипотенциальную поверхность (то есть разность потенциалов между произвольной точкой на высоте 2 м и поверхностью Земли — около 200 вольт, однако разность потенциалов между головой человека и поверхностью Земли, на которой она стоит — близка к нулю).
Общая разность потенциалов между Землёй и ионосферой составляет 400000 вольт[25].
Электрическое поле Земли влияет на движение заряженных частиц в атмосфере. Положительно заряженные частицы движутся в ней вниз, а отрицательно заряженные — вверх. Заряженные частицы постоянно образуются в атмосфере под действием космических лучей, благодаря чему в ней поддерживается постоянный ток с силой 10−12 ампер на каждый квадратный метр[25].
Безопасность в зоне электрического поля
Электрическое поле возникает при наличии напряжения на токоведущих частях электроустановок.
Пространство, в котором напряжённость электрического поля равна 5 кВ/м и больше, принято называть опасной зоной или зоной влияния. Приближённо можно считать, что эта зона лежит в пределах круга с центром в точке расположения ближайшей токоведущей части, находящейся под напряжением, и радиусом R = 20 м для электроустановок 400—500 кВ и R = 30 м для электроустановок 750 кВ.
В ОРУ 110 кВ и выше и на ВЛ 330 кВ и выше при выполнении работ в зоне влияния электрического поля напряжённостью свыше 5 кВ/м необходимо ограничивать длительность пребывания людей согласно требованиям ГОСТ 12.1.002 или применять средства защиты от воздействия электрического поля (далее — средства защиты).
При напряжённости электрического поля до 5 кВ/м длительность пребывания в нём не ограничивается.
Допустимая продолжительность Т (в часах) пребывания в электрическом поле напряжённостью в от 5 до 20 кВ/м включительно вычисляется по формуле: часов, где Е — напряжённость (выраженная в кВ/м) действующего электрического поля в контролируемой зоне.
Продолжительность работы в электрическом поле напряжённостью от 20 до 25 кВ/м не должна превышать 10 мин. При напряженности свыше 25 кВ/м следует применять средства защиты, позволяющие работать полный рабочий день.
Вышеизложенные требования действительны при условии исключения возможности воздействия на работников электрических разрядов.
Допустимая продолжительность пребывания в зоне воздействия электрического поля без средств защиты может быть реализована единоразово или с перерывами в течение рабочего дня. В течение остального времени следует применять средства защиты или находиться в электрическом поле напряженностью до 5 кВ/м.
В различных точках пространства вблизи электроустановок напряжённость электрического поля имеет разные значения и зависит от ряда факторов: номинального напряжения, расстояния (по высоте и горизонтали) рассматриваемой точки от токоведущих частей и др.
Продолжительность пребывания человека в контролируемой зоне устанавливается с учётом наибольшего значения измеренной напряжённости.
Наряду с биологическим действием электрическое поле обусловливает возникновение разрядов между человеком и металлическим предметом, имеющим иной по сравнению с телом человека потенциал. Если человек стоит непосредственно на земле или на токопроводящем заземлённом основании, то потенциал его тела практически равен нулю, а если он изолирован от земли, то тело оказывается под некоторым потенциалом, достигающим иногда нескольких киловольт.
Очевидно, что прикосновение человека, изолированного от земли, к заземленному металлическому предмету, равно как и прикосновение заземлённого человека к металлическому предмету, изолированному от земли, сопровождается прохождением через человека в землю разрядного тока, который может вызывать болезненные ощущения, особенно в первый момент. Часто прикосновение сопровождается искровым разрядом. В случае прикосновения к изолированному от земли металлическому предмету большой протяжённости (трубопровод, проволочная ограда на деревянных стойках и т. п. или большого размера металлическая крыша деревянного здания и пр.) сила тока, проходящего через человека, может достигать значений, опасных для жизни.
Допустимое значение тока, длительно проходящего через человека и обусловленного воздействием электрического поля электроустановок сверхвысокого напряжения, составляет примерно 50—60 мкА, что соответствует напряжённости электрического поля на высоте роста человека примерно 5 кВ/м. Если при электрических разрядах, возникающих в момент прикосновения человека к металлической конструкции, имеющей иной, чем человек, потенциал, установившийся ток не превышает 50— 60 мкА, то человек, как правило, не испытывает болевых ощущений. Поэтому это значение тока принято в качестве нормативного (допустимого).
Основными средствами коллективной защиты от воздействия электрического поля промышленной частоты являются стационарные и переносные разновидности экранирующих устройств.
Переносные и передвижные экранирующие устройства необходимо заземлять на месте их установки с помощью присоединения к заземляющему устройству или металлическим конструкциям, которые соединены с заземляющим устройством, гибким медным проводником сечением не менее 4 мм2.
Съёмные экранирующие устройства должны иметь гальваническое соединение с механизмами, на которых они установлены. Для заземления машин и механизмов дополнительного заземления съёмных экранирующих устройств не требуется.
Заземление индивидуальных экранирующих комплектов осуществляется с помощью специальной обуви с токопроводящей подошвой. При выполнении работ в положении стоя на изолирующем основании (деревянный настил, изолятор, окрашенный металл) или работ, связанных с прикосновением к заземлённым конструкциям незащищенной рукой (при снятых перчатках или рукавицах), экранирующую одежду следует дополнительно заземлить путём присоединения её специальным гибким проводником сечением 4 мм2 к заземлённой конструкции или к заземляющему устройству.
Запрещается применение индивидуальных экранирующих комплектов при работе, если не исключена возможность прикосновения к токоведущим частям, находящимся под напряжением до 1000 В, а также при испытаниях оборудования (для работников, которые непосредственно проводят испытания повышенным напряжением) и электросварочных работ. Защита работников в этом случае должна осуществляться с применением экранирующих устройств.
При выполнении работ на участках отключенных токоведущих частей, находящихся в зоне влияния электрического поля, для снятия наведенного потенциала их следует заземлять.
Запрещается прикасаться к отключенным, но не заземлённым токоведущим частям без средств защиты.
Ремонтные приспособления и оснастка, которые могут оказаться изолированными от земли, также должны быть заземлены.
Машины и механизмы на пневмоколёсном ходу, находящиеся в зоне влияния электрического поля, необходимо заземлять. Во время их передвижения в этой зоне для съёма приведённого потенциала следует применять металлическую цепь, присоединённую к шасси или к кузову и касающуюся земли.
Запрещается заправлять машины и механизмы горючими и смазочными материалами в зоне влияния электрического поля.
При подъёме на оборудование и конструкции, расположенные в зоне влияния электрического поля, следует применять средства защиты независимо от значения напряжённости электрического поля и продолжительности работы в нём. В случае поднятия с помощью телескопической вышки или гидроподъёмника их корзины (люльки) следует оборудовать экраном или применять экранирующие комплекты.
В заземлённых кабинах и кузовах машин, механизмов, передвижных мастерских и лабораторий, в зданиях из железобетона, в кирпичных зданиях с железобетонным перекрытием, металлическим каркасом или заземлённой металлической кровлей электрическое поле отсутствует и применения средств защиты не требуется.
Примечания
- ↑ Purcell Edward M., Morin David J. Electricity and Magnetism. — 3rd. — New York : Cambridge University Press, 2013. — P. 14–20. — ISBN 978-1-107-01402-2.
- ↑ Browne, p 225: «… around every charge there is an aura that fills all space. This aura is the electric field due to the charge. The electric field is a vector field… and has a magnitude and direction.»
- ↑ Richard Feynman. The Feynman Lectures on Physics Vol II. — Addison Wesley Longman, 1970. — P. 1—3,1-4. — ISBN 978-0-201-02115-8.
- ↑ Purcell. Electricity and Magnetism. — Cambridge University Press, 2013. — P. 15–16. — ISBN 978-1-107-01402-2.
- ↑ Serway. College Physics, 10th Ed.. — Cengage Learning. — P. 532–533. — ISBN 978-1305142824.
- ↑ Sears, Francis (1982), University Physics, Sixth Edition, Addison Wesley, ISBN 0-201-07199-1
- ↑ См. параграф Преобразования Лоренца для электромагнитного поля (ф-лы 6.38) курса «Электричество и магнетизм» на сайте МИФИ, кафедра общей физики.
- ↑ Umashankar, Korada (1989), Introduction to Engineering Electromagnetic Fields, World Scientific, ISBN 9971-5-0921-0
- ↑ Griffiths, David J. (David Jeffery), 1942-. Introduction to electrodynamics. — 3rd. — Upper Saddle River, N.J. : Prentice Hall, 1999. — ISBN 0-13-805326-X.
- ↑ Morely & Hughes, Principles of Electricity, Fifth edition, ISBN 0-582-42629-4
- ↑ Tou. Visualization of Fields and Applications in Engineering. — John Wiley and Sons. — P. 64. — ISBN 9780470978467.
- ↑ Гринберг Г. А. Избранные вопросы математической теории электрических и магнитных явлений. — М.: АН СССР, 1948. — 727 с.
- ↑ Миролюбов Н. Н., Костенко М. В., Левинштейн М. Л. Методы расчета электростатических полей. — М.: Высшая школа, 1963. — 416 с.
- ↑ Смайт В. Электростатика и электродинамика. — М.: ИЛ, 1954. — 604 с.
- ↑ 1 2 Колечицкий Е. С. Расчет электрических полей устройств высокого напряжения. — М.: Энергоатомиздат, 1983. — 168 с.
- ↑ gwrowe. Curl & Potential in Electrostatics. physicspages.com (8 октября 2011). Дата обращения: 2 ноября 2020. Архивировано 22 марта 2019 года.
- ↑ Huray. Maxwell's Equations. — ISBN 978-0-470-54276-7.
- ↑ Purcell, pp. 5-7.
- ↑ Salam, Abdus (16 December 1976). "Quarks and leptons come out to play". New Scientist. 72.
- ↑ Electromagnetism (2nd Edition), I.S. Grant, W.R. Phillips, Manchester Physics, John Wiley & Sons, 2008, ISBN 978-0-471-92712-9
- ↑ Electricity and Modern Physics (2nd Edition), G.A.G. Bennet, Edward Arnold (UK), 1974, ISBN 0-7131-2459-8
- ↑ Landau Lev Davidovich, Lifshitz Evgeny M. Electrodynamics of Continuous Media : [англ.]. — Pergamon, 1963. — Vol. 8. — P. 285. — «In Maxwell's equations… ε is a function of the co-ordinates.». — ISBN 978-0-7581-6499-5.
- ↑ Introduction to Electrodynamics (3rd Edition), D.J. Griffiths, Pearson Education, Dorling Kindersley, 2007, ISBN 81-7758-293-3
- ↑ Fedosin S.G. The Integral Theorem of the Field Energy. Gazi University Journal of Science. Vol. 32, No. 2, pp. 686-703 (2019). http://dx.doi.org/10.5281/zenodo.3252783. // Интегральная теорема энергии поля.
- ↑ 1 2 3 Electricity in the Atmosphere (англ.)
Литература
- Purcell, Edward. ELECTRICITY AND MAGNETISM / Purcell, Edward, Morin, David. — 3rd. — Cambridge University Press, New York, 2013. — ISBN 978-1-107-01402-2.
- Browne, Michael. PHYSICS FOR ENGINEERING AND SCIENCE. — 2nd. — McGraw-Hill, Schaum, New York, 2011. — ISBN 978-0-07-161399-6.













































![{\displaystyle \mathbf {F} =q\mathbf {E} +q\left[\mathbf {v} \times \mathbf {B} \right]}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/04c3a95620366e7986135198e9c0b7ed884c0094)












