Распределение Райса

Распределение Райса
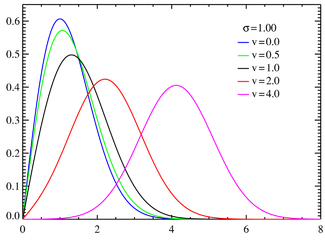Плотность распределения Райса для различных значений параметра ν   при σ = 1. 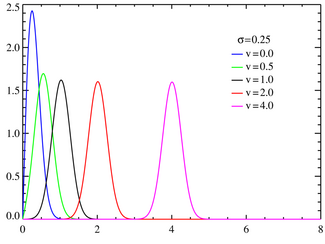Плотность распределения Райса для различных значений параметра ν   при σ = 0.25.Плотность вероятности
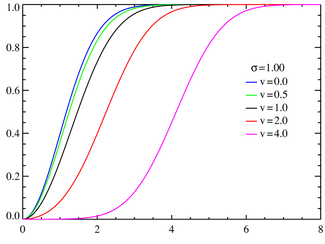Функция распределения Райса для различных значений параметра ν   при σ = 1. 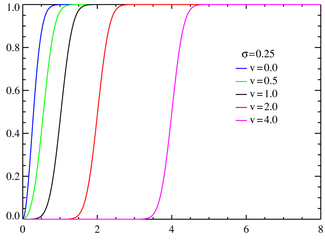Функция распределения Райса для различных значений параметра ν   при σ = 0.25.Функция распределения
Параметры	$\nu \geq 0\,$ $\sigma \geq 0\,$
Носитель	x ∈ [0, +∞)
Плотность вероятности	${\frac {x}{\sigma ^{2}}}\exp \left({\frac {-(x^{2}+\nu ^{2})}{2\sigma ^{2}}}\right)I_{0}\left({\frac {x\nu }{\sigma ^{2}}}\right)$
Функция распределения	$1-Q_{1}\left({\frac {\nu }{\sigma }},{\frac {x}{\sigma }}\right)$ где Q1 - это Q-функция Маркума
Математическое ожидание	$\sigma {\sqrt {\pi /2}}\,\,L_{1/2}(-\nu ^{2}/2\sigma ^{2})$
Дисперсия	$2\sigma ^{2}+\nu ^{2}-{\frac {\pi \sigma ^{2}}{2}}L_{1/2}^{2}\left({\frac {-\nu ^{2}}{2\sigma ^{2}}}\right)$

Распределение Райса является обобщением распределения Рэлея. Введено американским ученым Стефаном Райсом.

Если ${X}$ и ${Y}$ — независимые случайные величины, имеющие нормальное распределение с одинаковыми дисперсиями ${\sigma }^{2}$ и ненулевыми математическими ожиданиями (в общем случае неравными), то величина $Z={\sqrt {X^{2}+Y^{2}}}$ имеет распределение Райса, плотность вероятности которой определяется в виде

$f(x|\nu ,\sigma )={\frac {x}{\sigma ^{2}}}\exp \left({\frac {-(x^{2}+\nu ^{2})}{2\sigma ^{2}}}\right)I_{0}\left({\frac {x\nu }{\sigma ^{2}}}\right),$

где I₀(z) — модифицированная функция Бесселя нулевого порядка.

Применение

• Распределение Райса часто используют для описания амплитудных флуктуаций радиосигнала, в том числе в многолучевых каналах распространения радиосигнала.

Связь с другими распределениями

• Если $X\!$ и $Y\!$ — независимые случайные величины, имеющие нормальное распределение с нулевыми математическими ожиданиями и одинаковыми дисперсиями $\sigma ^{2}\!$, то случайная величина $Z={\sqrt {X^{2}+Y^{2}}}$ имеет распределение Рэлея.

См. также

• Распределение Рэлея
• Нормальное распределение

Литература

1. Перов, А. И. Статистическая теория радиотехнических систем. — М.: Радиотехника, 2003. — 400 с. — ISBN 5-93108-047-3.