Гипергеометрическое распределение: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
Нет описания правки |
добавление изображения |
||
| Строка 2: | Строка 2: | ||
name =Гипергеометрическое распределение| |
name =Гипергеометрическое распределение| |
||
type =Функция| |
type =Функция| |
||
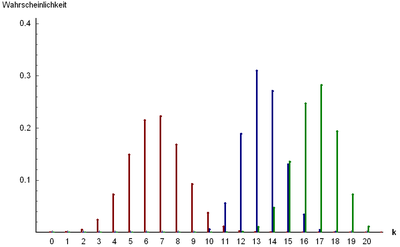
pdf_image =[[File:Hypergeometrische Verteilung.PNG|мини|400px|Функция вероятности для <math>n=20</math>; <math>M=20, N=30</math> (голубой), <math>M=50, N=60</math> (зелёный) и <math>M=20, N=60</math> (красный)]]| |
|||
pdf_image =| |
|||
cdf_image =| |
cdf_image =| |
||
notation =<math>\mathrm{HG}(D,n,N)\,</math>| |
notation =<math>\mathrm{HG}(D,n,N)\,</math>| |
||
| Строка 14: | Строка 14: | ||
variance =<math>n(D/N)(1-D/N)(N-n)\over (N-1)</math>| |
variance =<math>n(D/N)(1-D/N)(N-n)\over (N-1)</math>| |
||
skewness =<math>\frac{(N-2D)(N-1)^\frac{1}{2}(N-2n)}{[nD(N-D)(N-n)]^\frac{1}{2}(N-2)}</math>| |
skewness =<math>\frac{(N-2D)(N-1)^\frac{1}{2}(N-2n)}{[nD(N-D)(N-n)]^\frac{1}{2}(N-2)}</math>| |
||
kurtosis =<math> \left[\frac{N^2(N-1)}{n(N-2)(N-3)(N-n)}\right]\times</math><br /><math>\times \left[\frac{N(N+1)-6N(N-n)}{D(N-D)}+\frac{3n(N-n)(N+6)}{N^2}-6\right]</math>| |
kurtosis =<math> \left[\frac{N^2(N-1)}{n(N-2)(N-3)(N-n)}\right]\times</math><br /><math>\times \left[\frac{N(N+1)-6N(N-n)}{D(N-D)}+ |
||
\frac{3n(N-n)(N+6)}{N^2}-6\right]</math>| |
|||
entropy =| |
entropy =| |
||
mgf =<math>\frac{{N-D \choose n}}{{N \choose n}}\,_2F_1(-n,-D;N-D-n+1;e^{t})</math>| |
mgf =<math>\frac{{N-D \choose n}}{{N \choose n}}\,_2F_1(-n,-D;N-D-n+1;e^{t})</math>| |
||
Версия от 08:25, 20 августа 2012
| Гипергеометрическое распределение | |
|---|---|
 | |
| Обозначение | |
| Параметры |
|
| Носитель | |
| Функция вероятности | |
| Математическое ожидание | |
| Мода | |
| Дисперсия | |
| Коэффициент асимметрии | |
| Коэффициент эксцесса |
|
| Производящая функция моментов | |
| Характеристическая функция | |
Гипергеометри́ческое распределе́ние в теории вероятностей моделирует количество удачных выборок без возвращения из конечной совокупности.
Пример
| вытянутые | не вытянутые | всего | |
|---|---|---|---|
| с дефектом | k | D − k | D |
| без дефекта | n − k | N + k − n − D | N − D |
| всего | n | N − n | N |
Типичный пример представлен вышестоящей таблицей: осуществлена поставка из N объектов, из которых D имеют дефект. Гипергеометрическое распределение описывает вероятность того, что в выборке из n различных объектов, вытянутых из поставки, ровно k объектов являются бракованными.
В общем, если случайная величина X соответствует гипергеометрическому распределению с параметрами N, D и n, то вероятность получения ровно k успехов определяется формулой:
Эта вероятность положительна когда k лежит в промежутке между max{ 0, D + n − N } и min{ n, D }.
Приведенная формула может трактоваться следующим образом: существует возможных выборок(без возвращения). Есть способов выбрать k бракованных объектов и способов заполнить остаток выборки объектами без дефектов.
В случае, когда размер популяции является большим по сравнению с размером выборки(т.е., N намного больше чем n) гипергеометрическое распределение хорошо аппроксимируется биномиальным распределением с параметрами n (количество испытаний) и p = D / N (вероятность успеха в одном испытании).
Определение
Пусть имеется конечная совокупность, состоящая из элементов. Предположим, что (defective) из них обладают нужным нам свойством. Оставшиеся этим свойством не обладают. Случайным образом из общей совокупности выбирается группа из элементов. Пусть - случайная величина, равная количеству выбранных элементов, обладающих нужным свойством. Тогда функция вероятности имеет вид:
- ,
где обозначает биномиальный коэффициент. Пишем: .
Моменты
- ,
- .
Пример применения
Классическим применением гипергеометрического распределения является выборка без возвращения. Рассмотрим урну с двумя типами шаров: черными и белыми. Определим вытягивание белого шара как успех, а черного как неудачу. Если N является числом всех шаров в урне и D является числом белых шаров, то N − D является числом черных шаров.
Теперь предположим, что в урне находятся 5 белых и 45 черных шаров. Стоя рядом с урной, вы закрываете глаза и вытаскиваете 10 шаров. Какова вероятность p (k=4) вытянуть 4 белых шара (и, соответственно, 6 черных шаров) ?
Задача описывается следующей таблицей:
| вытянутые | не вытянутые | всего | |
|---|---|---|---|
| белые шары | 4 (k) | 1 = 5 − 4 (D − k) | 5 (D) |
| чёрные шары | 6 = 10 − 4 (n − k) | 39 = 50 + 4 − 10 − 5 (N + k − n − D) | 45 (N − D) |
| всего | 10 (n) | 40 (N − n) | 50 (N) |
Вероятность Pr (k = x) того, что будут вытянуты ровно x белых шаров (= количество успехов), может быть посчитана с помощью формулы:
Отсюда, в нашем примере (x = 4), получим:
Таким образом, вероятность вытянуть ровно 4 белых шара достаточно мала (примерно 0.004). Это значит, что при проведении эксперимента (вытаскивание 10 шаров из урны с 50 шарами без возвращения) 1000 раз мы рассчитываем получить вышеупомянутый результат 4 раза.
Что касается вероятности вытянуть все 5 белых шаров, то интуитивно понятно, что она будет меньше, чем вероятность вытянуть 4 белых шара. Давайте посчитаем эту вероятность.
| вытянутые | не вытянутые | всего | |
|---|---|---|---|
| белые шары | 5 (k) | 0 = 5 − 5 (D − k) | 5 (D) |
| чёрные шары | 5 = 10 − 5 (n − k) | 40 = 50 + 5 − 10 − 5 (N + k − n − D) | 45 (N − D) |
| всего | 10 (n) | 40 (N − n) | 50 (N) |
Таким образом, мы получаем вероятность:
Как и ожидалось, вероятность вытянуть 5 белых шаров меньше, чем вероятность вытянуть 4 белых шара.
Заключение:
Начальный вопрос можно расширить следующим образом:
Если вытягиваются 10 шаров из урны (содержащей 5 белых и 45 чёрных шаров), какова вероятность вытянуть не менее 4 белых шаров?
Для получения ответа на этот вопрос необходимо посчитать функцию распределения p(k>=4).
Так как гипергеометрическое распределение является дискретным вероятностным распределением, функция распределения может быть легко посчитана как сумма соответствующих вероятностей.
В нашем примере достаточно сложить Pr (k = 4) и Pr (k = 5):
- Pr (k ≥ 4) = 0.003964583 + 0.0001189375 = 0.004083520
Симметричность
Эта симметричность интуитивно понятна, если перекрасить белые шары в черные и наоборот, таким образом, белые и черные шары просто меняются ролями.
Эта симметричность интуитивно понятна, если вместо вытягивания шаров, вы помечаете шары, которые вы бы вытянули. Оба выражения дают вероятность того, что ровно k шаров черные и помечены как вытянутые.
Связь с другими распределениями
- Зафиксируем и и устремим к бесконечности. Тогда сходится к биномиальному распределению .
Для улучшения этой статьи желательно:
|













![{\displaystyle {\frac {(N-2D)(N-1)^{\frac {1}{2}}(N-2n)}{[nD(N-D)(N-n)]^{\frac {1}{2}}(N-2)}}}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/d2951c09a7efa8a1b66a01cbdf643fa58b8bc32d)
![{\displaystyle \left[{\frac {N^{2}(N-1)}{n(N-2)(N-3)(N-n)}}\right]\times }](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/94fa0f5c723926c014aff37a246a5f06b619478e)
![{\displaystyle \times \left[{\frac {N(N+1)-6N(N-n)}{D(N-D)}}+{\frac {3n(N-n)(N+6)}{N^{2}}}-6\right]}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/ab0071274c09e48ec5b816e849eff71482693b71)














![{\displaystyle \mathbb {E} [Y]={\frac {nD}{N}}}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/68a0cb209bb9f59424d26accc99f2c3fd6ec1053)
![{\displaystyle \mathrm {D} [Y]={n(D/N)(1-D/N)(N-n) \over (N-1)}}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/de2a1d1cbedf97564899d3db54f0d64e500c2c90)






