Праймориал: различия между версиями
| [отпатрулированная версия] | [отпатрулированная версия] |
м →Свойства и приложения: викификация |
|||
| Строка 64: | Строка 64: | ||
Праймориалы играют важную роль в поиске простых чисел в [[Арифметические прогрессии из простых чисел|арифметических прогрессиях из простых чисел]]. Например, сложение чисел 2236133941 + 23# даёт в результате простое число, начинающее последовательность из тринадцати простых чисел, которые можно получить, последовательно прибавляя 23#, и заканчивающуюся числом 5136341251. 23# является также общей разностью в арифметических прогрессиях из пятнадцати и шестнадцати простых чисел. |
Праймориалы играют важную роль в поиске простых чисел в [[Арифметические прогрессии из простых чисел|арифметических прогрессиях из простых чисел]]. Например, сложение чисел 2236133941 + 23# даёт в результате простое число, начинающее последовательность из тринадцати простых чисел, которые можно получить, последовательно прибавляя 23#, и заканчивающуюся числом 5136341251. 23# является также общей разностью в арифметических прогрессиях из пятнадцати и шестнадцати простых чисел. |
||
Каждое [[Сверхсоставное число|многосоставное |
Каждое [[Сверхсоставное число|многосоставное число]] можно представить в виде произведения праймориалов (например, 360 = 2 · 6 · 30)<ref>[http://oeis.org/A002182 A002182 — OEIS<!-- Заголовок добавлен ботом -->]</ref>. |
||
Все праймориалы являются [[Бесквадратное число|бесквадратными числами]], и каждый из них имеет [[Простой множитель|простые делители]] любого числа меньшего, чем праймориал. Для каждого праймориала ''n'' отношение <math>\phi(n)/n</math> меньше, чем для любого целого числа, где <math>\phi</math> является [[Функция Эйлера|функцией Эйлера]]. |
Все праймориалы являются [[Бесквадратное число|бесквадратными числами]], и каждый из них имеет [[Простой множитель|простые делители]] любого числа меньшего, чем праймориал. Для каждого праймориала ''n'' отношение <math>\phi(n)/n</math> меньше, чем для любого целого числа, где <math>\phi</math> является [[Функция Эйлера|функцией Эйлера]]. |
||
Версия от 13:39, 14 марта 2019
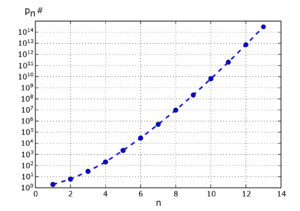

Праймориал (англ. Primorial, иногда именуется также «примориал») — в теории чисел функция над рядом натуральных чисел, схожая с функцией факториала, с разницей в том, что праймориал является последовательным произведением простых чисел, меньших или равных данному, в то время как факториал является последовательным произведением всех натуральных чисел, меньших или равных данному.
Термин «праймориал» ввёл в научный оборот американский инженер и математик Харви Дабнер[англ.][1].
Определение для простых чисел
Для n-го простого числа pn праймориал pn# определён как произведение первых n простых чисел[2][3]:
где pk — k-е простое число.
Например, p5# обозначает произведение первых 5 простых чисел:
Таким образом, первые шесть праймориалов:
- 1, 2, 6, 30, 210, 2310 (последовательность A002110 в OEIS, также включает p0# = 1 как пустое произведение[англ.]).
Асимптотически праймориалы pn# растут в соответствии с
где является нотацией «o» малого[3].
Определение для натуральных чисел
В общем случае для целого положительного числа n праймориал n# может быть определён как произведение простых чисел, меньших или равных n[2][4]:
где является функцией распределения простых чисел (последовательность A000720 в OEIS), дающая количество простых чисел ≤ n, что эквивалентно
Например, 12# представляет собой произведение простых чисел, каждое из которых ≤ 12:
Таким образом, может быть вычислено как
Рассмотрим первые 12 праймориалов:
- 1, 2, 6, 6, 30, 30, 210, 210, 210, 210, 2310, 2310.
Мы видим, что для составных чисел каждый член данной последовательности просто дублирует предыдущий. В приведенном выше примере мы имеем, что 12# = p5# = 11#, поскольку 12 является составным числом.
Натуральный логарифм n# — это первая функция Чебышева, записанная в виде или , что приближается к линейной n для больших значений n[5].
Праймориалы n# растут в соответствии с
Свойства и приложения
Праймориалы играют важную роль в поиске простых чисел в арифметических прогрессиях из простых чисел. Например, сложение чисел 2236133941 + 23# даёт в результате простое число, начинающее последовательность из тринадцати простых чисел, которые можно получить, последовательно прибавляя 23#, и заканчивающуюся числом 5136341251. 23# является также общей разностью в арифметических прогрессиях из пятнадцати и шестнадцати простых чисел.
Каждое многосоставное число можно представить в виде произведения праймориалов (например, 360 = 2 · 6 · 30)[6].
Все праймориалы являются бесквадратными числами, и каждый из них имеет простые делители любого числа меньшего, чем праймориал. Для каждого праймориала n отношение меньше, чем для любого целого числа, где является функцией Эйлера.
Каждый праймориал является слабо тотиентным числом[англ.][7].
Аппроксимация
Дзета-функция Римана для положительных чисел, больших единицы, может быть выражена[8] с использованием праймориала и функции Жордана[англ.]* :
Таблица значений
| n | n# | pn | pn# |
|---|---|---|---|
| 0 | 1 | не существует | 1 |
| 1 | 1 | 2 | 2 |
| 2 | 2 | 3 | 6 |
| 3 | 6 | 5 | 30 |
| 4 | 6 | 7 | 210 |
| 5 | 30 | 11 | 2310 |
| 6 | 30 | 13 | 30030 |
| 7 | 210 | 17 | 510510 |
| 8 | 210 | 19 | 9699690 |
| 9 | 210 | 23 | 223092870 |
| 10 | 210 | 29 | 6469693230 |
| 11 | 2310 | 31 | 200560490130 |
| 12 | 2310 | 37 | 7420738134810 |
| 13 | 30030 | 41 | 304250263527210 |
| 14 | 30030 | 43 | 13082761331670030 |
| 15 | 30030 | 47 | 614889782588491410 |
| 16 | 30030 | 53 | 32589158477190044730 |
| 17 | 510510 | 59 | 1922760350154212639070 |
| 18 | 510510 | 61 | 117288381359406970983270 |
| 19 | 9699690 | 67 | 7858321551080267055879090 |
| 20 | 9699690 | 71 | 557940830126698960967415390 |
Композиториал
Композиториал числа n в отличие от праймориала является произведением составных чисел, меньших чем n. Композиториал равен отношению факториала и праймориала числа: . Первые пятнадцать композиториалов (исключая повторяющиеся значения) равны 1, 4, 24, 192, 1728, 17280, 207360, 2903040, 43545600, 696729600, 12541132800, 250822656000, 5267275776000, 115880067072000[9][10][11].
См. также
Примечания
- ↑ Dubner, 1987, pp. 197–203.
- ↑ 1 2 Weisstein, Eric W. Primorial (англ.) на сайте Wolfram MathWorld.
- ↑ 1 2 последовательность A002110 в OEIS.
- ↑ последовательность A034386 в OEIS.
- ↑ Weisstein, Eric W. Chebyshev Functions (англ.) на сайте Wolfram MathWorld.
- ↑ A002182 — OEIS
- ↑ On sparsely totient numbers
- ↑ István Mező. The Primorial and the Riemann zeta function : [англ.] // The American Mathematical Monthly. — 2013. — Vol. 120. — P. 321.
- ↑ compositorials (англ.). www.numbersaplenty.com. Дата обращения: 1 февраля 2018.
- ↑ последовательность A036691 в OEIS
- ↑ Compositorial - OeisWiki (англ.). oeis.org. Дата обращения: 1 февраля 2018.
Литература
- Harvey Dubner. Factorial and primorial primes // Journal of Recreational Mathematics. — 1987. — Vol. 19. — P. 197–203.


![{\displaystyle p_{n}\#=e^{[1+o(1)]n\log n},}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/fda5104d6fd3d640760fa2ac3594d74f9edb6bea)














