Квадратное уравнение
Квадра́тное уравне́ние — алгебраическое уравнение второй степени с общим видом
в котором — неизвестное, а коэффициенты , и — вещественные или комплексные числа.
Корень уравнения — это значение неизвестного , обращающее квадратный трёхчлен в ноль, а квадратное уравнение в верное числовое равенство. Также это значение называется корнем самого многочлена
Элементы квадратного уравнения имеют собственные названия[1]:
- называют первым или старшим коэффициентом,
- называют вторым, средним коэффициентом или коэффициентом при ,
- называют свободным членом.
Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице[1]. Такое уравнение может быть получено делением всего выражения на старший коэффициент :
Полным называют такое квадратное уравнение, все коэффициенты которого отличны от нуля.
Неполным называется такое квадратное уравнение, в котором хотя бы один из коэффициентов, кроме старшего (либо второй коэффициент, либо свободный член), равен нулю.
Квадратное уравнение является разрешимым в радикалах, то есть его корни могут быть выражены через коэффициенты в общем виде.
Исторические сведения о квадратных уравнениях
Древний Вавилон
Уже во втором тысячелетии до нашей эры вавилоняне знали, как решать квадратные уравнения[1]. Решение их в Древнем Вавилоне было тесно связано с практическими задачами, в основном такими, как измерение площади земельных участков, земельные работы, связанные с военными нуждами; наличие этих познаний также обусловлено развитием математики и астрономии вообще. Были известны способы решения как полных, так и неполных квадратных уравнений. Приведём примеры квадратных уравнений, решавшихся в Древнем Вавилоне, используя современную алгебраическую запись:
Правила решения квадратных уравнений во многом аналогичны современным, однако в вавилонских текстах не зафиксированы рассуждения, путём которых эти правила были получены.
Индия
Задачи, решаемые с помощью квадратных уравнений, встречаются в трактате по астрономии «Ариабхаттиам», написанным индийским астрономом и математиком Ариабхатой в 499 году нашей эры. Один из первых известных выводов формулы корней квадратного уравнения принадлежит индийскому учёному Брахмагупте (около 598 г.)[1]; Брахмагупта изложил универсальное правило решения квадратного уравнения, приведённого к каноническому виду: притом предполагалось, что в нём все коэффициенты, кроме могут быть отрицательными. Сформулированное учёным правило по своему существу совпадает с современным.
Корни квадратного уравнения на множестве действительных чисел
I способ. Общая формула для вычисления корней с помощью дискриминанта
Дискриминантом квадратного уравнения называется величина .
| Условие | |||
| Количество корней | Два корня | Один корень кратности 2 (другими словами, два равных корня) |
Действительных корней нет |
| Формула | — |
- Формулу (1) можно получить следующим образом:
- Умножаем каждую часть на и прибавляем :
- Формула для случая является частным случаем формулы (1):
- Для случая отсутствие вещественных корней также следует из формулы (1), поскольку квадратный корень из отрицательного числа не принадлежит множеству вещественных чисел.
Данный метод универсальный, однако не единственный.
II способ. Корни квадратного уравнения при чётном коэффициенте b
Для уравнений вида , то есть при чётном , где
вместо формулы (1) для нахождения корней существует возможность использования более простых выражений[1].
Примечание: данные ниже формулы можно получить, подставив в стандартные формулы выражение b = 2k, через несложные преобразования.
| неприведённое | приведённое | D > 0 | неприведённое | приведённое |
| удобнее вычислять значение
четверти дискриминанта: Все необходимые свойства при этом сохраняются. |
. | |||
| D = 0 | ||||
III способ. Решение неполных квадратных уравнений
К решению неполных квадратных уравнений практикуется особый подход. Рассматриваются три возможных ситуации.
|
Если , то уравнение имеет два действительных корня (разных по знаку), a если , то уравнение не имеет действительных корней. |
или Такое уравнение обязательно имеет два действительных корня, причём один из них всегда равен нулю. |
IV способ. Использование частных соотношений коэффициентов
Существуют частные случаи квадратных уравнений, в которых коэффициенты находятся в соотношениях между собой, позволяющих решать их гораздо проще.
Корни квадратного уравнения, в котором сумма старшего коэффициента и свободного члена равна второму коэффициенту
Если в квадратном уравнении сумма первого коэффициента и свободного члена равна второму коэффициенту: , то его корнями являются и число, противоположное отношению свободного члена к старшему коэффициенту ().
Способ 1. Сначала выясним, действительно ли такое уравнение имеет два корня (в том числе, два совпадающих):
- .
Да, это так, ведь при любых действительных значениях коэффициентов , а значит и дискриминант неотрицателен. Таким образом, если , то уравнение имеет два корня, если же , то оно имеет только один корень. Найдём эти корни:
- .
В частности, если , то корень будет один:
Способ 2.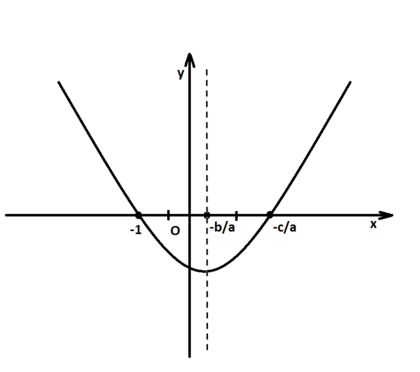
Используем геометрическую модель корней квадратного уравнения: их мы будем рассматривать как точки пересечения параболы с осью абсцисс. Всякая парабола вне зависимости от задающего её выражения является фигурой, симметричной относительно прямой . Это означает, что отрезок всякой перпендикулярной к ней прямой, отсекаемый на ней параболой, делится осью симметрии пополам. Сказанное, в частности, верно и для оси абсцисс. Таким образом, для всякой параболы справедливо одно из следующих равенств: (если ) или (если верно неравенство противоположного смысла). Используя тождество , выражающее геометрический смысл модуля, а также принимая, что (это можно доказать, подставив равенство в квадратный трёхчлен: , поэтому -1 - корень такого уравнения) , приходим к следующему равенству: Если учитывать, что разность в том случае, когда мы прибавляем модуль, всегда положительна, а в том, когда отнимаем - отрицательна, что говорит о тождественности этих случаев, и, к тому же, помня о равенстве , раскрываем модуль: . Во втором случае,совершив аналогичные преобразования, придём к тому же результату, ч.т.д.
- Отсюда следует, что перед решением какого-либо квадратного уравнения целесообразна проверка возможности применения к нему этой теоремы: сравнить сумму старшего коэффициента и свободного члена со вторым коэффициентом.
Корни квадратного уравнения, сумма всех коэффициентов которого равна нулю
Если в квадратном уравнении сумма всех его коэффициентов равна нулю (), то корнями такого уравнения являются и отношение свободного члена к старшему коэффициенту ().
Способ 1. Прежде всего заметим, что из равенства следует, что Установим количество корней:
При любых значениях коэффициентов уравнение имеет хотя бы один корень: действительно, ведь при любых значениях коэффициентов , а значит и дискриминант неотрицателен. Обратите внимание, что если , то уравнение имеет два корня, если же , то только один. Найдём эти корни:
что и требовалось доказать.
- В частности, если , то уравнение имеет только один корень, которым является число .
Способ 2. Пользуясь данным выше определением корня квадратного уравнения, обнаруживаем путём подстановки, что число 1 является таковым в рассматриваемом случае: - верное равенство, следовательно, единица - корень такого вида квадратных уравнений. Далее, по теореме Виета находим второй корень: согласно этой теореме, произведение корней уравнения равно числу, равному отношению свободного члена к старшему коэффициенту - , ч.т.д.
- Отсюда следует, что перед решением уравнения стандартными методами целесообразна проверка применимости к нему этой теоремы, а именно сложение всех коэффициентов данного уравнения и установление, не равна ли нулю эта сумма.
V способ. Разложение квадратного трёхчлена на линейные множители
Если трёхчлен вида удастся каким-либо образом представить в качестве произведения линейных множителей , то можно найти корни уравнения — ими будут и , действительно, ведь а решив указанные линейные уравнения, получим вышеописанное. Квадратный трёхчлен не всегда раскладывается на линейные множители с действительными коэффициентами: это возможно, если соответствующее ему уравнение имеет действительные корни.
Рассматриваются некоторые частные случаи.
Использование формулы квадрата суммы (разности)
Если квадратный трёхчлен имеет вид , то применив к нему названную формулу, можно разложить его на линейные множители и, значит, найти корни:
Выделение полного квадрата суммы (разности)
Также названную формулу применяют, пользуясь методом, получившим названия «выделение полного квадрата суммы (разности)». Применительно к приведённому квадратному уравнению с введёнными ранее обозначениями, это означает следующее:
- прибавляют и отнимают одно и то же число:
. - применяют формулу к полученному выражению, переносят вычитаемое и свободный член в правую часть:
- извлекают из левой и правой частей уравнения квадратный корень и выражают переменную:
Примечание: данная формула совпадает с предлагаемой в разделе «Корни приведённого квадратного уравнения», которую, в свою очередь, можно получить из общей формулы (1) путём подстановки равенства a = 1. Этот факт не просто совпадение: описанным методом, произведя, правда, некоторые дополнительные рассуждения, можно вывести и общую формулу, а также доказать свойства дискриминанта.
VI способ. Использование прямой и обратной теоремы Виета
Прямая теорема Виета (см. ниже) и обратная ей теорема позволяют решать приведённые квадратные уравнения устно, не прибегая к вычислениям по формуле (1).
Согласно обратной теореме, всякая пара чисел (число) , будучи решением системы уравнений
- являются корнями уравнения .
Подобрать устно числа, удовлетворяющие этим уравнениям, поможет прямая теорема. С её помощью можно определить знаки корней, не зная сами корни. Для этого следует руководствоваться правилом:
- 1) если свободный член отрицателен, то корни имеют различный знак, и наибольший по модулю из корней — знак, противоположный знаку второго коэффициента уравнения;
- 2) если свободный член положителен, то оба корня обладают одинаковым знаком, и это — знак, противоположный знаку второго коэффициента.
VII способ. Метод «переброски»
По своей сущности метод «переброски» является просто модификацией теоремы Виета.
Метод «переброски» — это сведение уравнения, которое нельзя привести так, чтобы все коэффициенты остались целыми, к приведённому уравнению с целыми коэффициентами:
- 1) умножаем обе части на старший коэффициент:
- 2) заменяем
Далее решаем уравнение относительно y по методу, описанному выше, и находим x = y/a.
Как можно заметить, в методе «переброски» старший коэффициент как раз «перебрасывается» к свободному члену.
Графическое решение квадратного уравнения
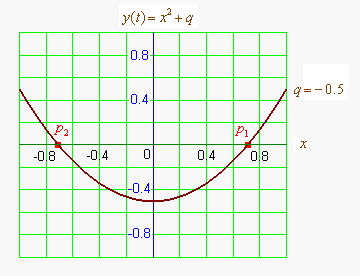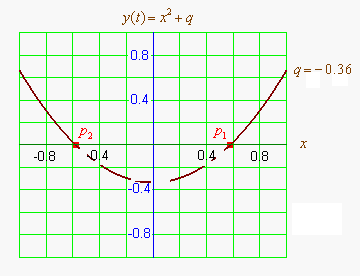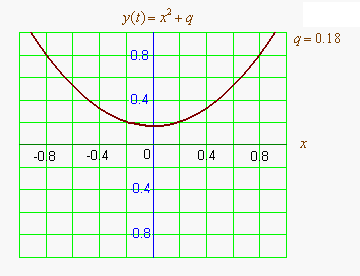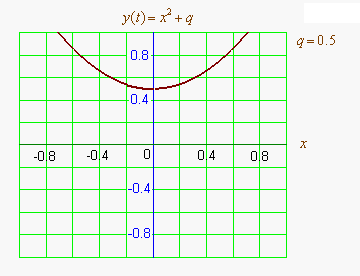
Графиком квадратичной функции является парабола. Решениями (корнями) квадратного уравнения называют абсциссы точек пересечения параболы с осью абсцисс. Если парабола, описываемая квадратичной функцией, не пересекается с осью абсцисс, уравнение не имеет вещественных корней. Если парабола пересекается с осью абсцисс в одной точке (в вершине параболы), уравнение имеет один вещественный корень (также говорят, что уравнение имеет два совпадающих корня). Если парабола пересекает ось абсцисс в двух точках, уравнение имеет два вещественных корня (см. изображение справа.)
Если коэффициент положительный, ветви параболы направлены вверх и наоборот. Если коэффициент положительный (при положительном , при отрицательном наоборот), то вершина параболы лежит в левой полуплоскости и наоборот.
Графический способ решения квадратных уравнений
Помимо универсального способа, описанного выше, существует так называемый графический способ. В общем виде этот способ решения рационального уравнения вида заключается в следующем: в одной системе координат строят графики функций и и находят абсциссы общих точек этих графиков; найденные числа и будут корнями уравнения.
- Есть всего пять основных способов графического решения квадратных уравнений.
Приём I
Для решения квадратного уравнения строится график функции и отыскиваются абсциссы точек пересечения такого графика с осью .
Приём II
Для решения того же уравнения этим приёмом уравнение преобразуют к виду и строят в одной системе координат графики квадратичной функции и линейной функции , затем находят абсциссу точек их пересечения.
Приём III
Данный приём подразумевает преобразование исходного уравнения к виду , используя метод выделения полного квадрата суммы (разности) и затем в . После этого строятся график функции (им является график функции , смещённый на единиц масштаба вправо или влево в зависимости от знака) и прямую , параллельную оси абсцисс. Корнями уравнения будут абсциссы точек пересечения параболы и прямой.
Приём IV
Квадратное уравнение преобразуют к виду , строят график функции (им является график функции , смещённый на единиц масштаба вверх, если этот коэффициент положителен, либо вниз, если он отрицателен), и , находят абсциссы их общих точек.
Приём V
Квадратное уравнение преобразуют к особому виду:
затем
Совершив преобразования, строят графики линейной функции и обратной пропорциональности , отыскивают абсциссы точек пересечения этих графиков. Этот приём имеет границу применимости: если , то приём не используется.
Решение квадратных уравнений с помощью циркуля и линейки
Описанные выше приёмы графического решения имеют существенные недостатки: они достаточно трудоёмки, при этом точность построения кривых — парабол и гипербол — низка. Указанные проблемы не присущи предлагаемому ниже методу, предполагающему относительно более точные построения циркулем и линейкой.
Чтобы произвести такое решение, нужно выполнить нижеследующую последовательность действий.
- Построить в системе координат окружность с центром в точке , пересекающую ось в точке .
- Далее возможны три случая:
- длина радиуса окружности превышает длину перпендикуляра к оси абсцисс, опущенного из точки : в этом случае окружность пересекает ось в двух точках, а уравнение имеет два действительных корня, равных абсциссам этих точек;
- радиус равен перпендикуляру: одна точка и один вещественный корень кратности 2;
- радиус меньше перпендикуляра: корней в множестве нет.

Рассматриваемый способ предполагает построение окружности, пересекающей ось ординат в точках (точке), абсциссы которых являются корнями (или корнем) решаемого уравнения. Как нужно строить такую окружность? Предположим, что она уже построена. Окружность определяется однозначно заданием трёх своих точек. Пусть в случае, если корня два, это будут точки , где , естественно, действительные корни квадратного уравнения (подчёркиваем: если они имеются). Найдём координаты центра такой окружности. Для этого докажем, что эта окружность проходит через точку . Действительно, согласно теореме о секущих, в принятых обозначениях выполняется равенство (см рисунок). Преобразовывая это выражение, получаем величину отрезка OD, которой и определяется искомая ордината точки D: (в последнем преобразовании использована теорема Виета (см. ниже в одноимённом разделе)). Если же корень один, то есть ось абсцисс будет касательной к такой окружности, и окружность пересекает ось y в точке с ординатой 1, то она обязательно пересечёт её и в точке с указанной выше ординатой (в частности, если 1=c/a, это могут быть совпадающие точки), что доказывается аналогично с использованием уже теоремы о секущей и касательной, являющаяся частным случаем теоремы о секущих. В первом случае (), определяющими будут точка касания, точка оси y с ординатой 1, и её же точка с ординатой . Если c/a и 1 - совпадающие точки, а корня два, определяющими будут эта точка и точки пересечения с осью абсцисс. В случае, когда (1=c/a) и корень один, указанных сведений достаточно для доказательства, так как такая окружность может быть только одна - её центром будет вершина квадрата, образуемого отрезками касательных и перпендикулярами, а радиус - стороне этого квадрата, составляющей 1. Пускай S - центр окружности, имеющей с осью абсцисс две общие точки. Найдём его координаты: для этого опустим от этой точки перпендикуляры к координатным осям. Концы этих перпендикуляров будут серединами отрезков AB и CD - ведь треугольники ASB и CSD равнобедренные, так как в них AS=BS=CS=DS как радиусы одной окружности, следовательно, высоты в них, проведённые к основаниям, также являются и медианами. Найдём координаты середин названных отрезков. Так как парабола симметрична относительно прямой , то точка этой прямой с такой же абсциссой будет являться серединой отрезка AB. Следовательно, абсцисса точки S равна этому числу. В случае же, если уравнение имеет один корень, то ось x является касательной по отношению к окружности,поэтому, согласно её свойству, её радиус перпендикулярен оси, следовательно, и в этом случае указанное число - абсцисса центра. Её ординату найдём так: . В третьем из возможных случаев, когда c\a=1 (и, значит, a=c), то .
Итак, нами найдены необходимые для построения данные. Действительно, если мы построим окружность с центром в точке , проходящую через точку , то она, в случаях, когда уравнение имеет действительные корни, пересечёт ось x в точках, абсциссы которых есть эти корни. Причём, если длина радиуса больше длины перпендикуляра к оси Ox, то уравнение имеет два корня (предположив обратное, мы бы получили противоречие с доказанным выше), если длины равны, то один (по той же причине), если же длина радиуса меньше длины перпендикуляра, то окружность не имеет общих точек с осью x, следовательно, и действительных корней у уравнения нет (доказывается тоже от противного: если корни есть, то окружность, проходящая через A, B, C совпадает с данной, и поэтому пересекает ось, однако она не должна пересекать ось абсцисс по условию, значит, предположение неверно).
Корни квадратного уравнения на множестве комплексных чисел
Уравнение с действительными коэффициентами
Квадратное уравнение с вещественными коэффициентами всегда имеет с учётом кратности два комплексных корня, о чём гласит основная теорема алгебры. При этом, в случае неотрицательного дискриминанта корни будут вещественными, а в случае отрицательного — комплексно-сопряжёнными:
- при уравнение будет иметь два вещественных корня:
- при — один корень кратности 2 (другими словами, два одинаковых корня):
- при — два комплексно-сопряжённых корня, выражающихся той же формулой, что и для положительного дискриминанта. Также её можно переписать так, чтобы она не содержала отрицательного подкоренного выражения, следующим образом:
Уравнение с комплексными коэффициентами
В комплексном случае квадратное уравнение решается по той же формуле (1) и указанным выше её вариантам, но различимыми являются только два случая: нулевого дискриминанта (один двукратный корень) и ненулевого (два корня единичной кратности).
Корни приведённого квадратного уравнения
Квадратное уравнение вида в котором старший коэффициент равен единице, называют приведённым. В этом случае формула для корней (1) упрощается до
Мнемонические правила:
- Из «Радионяни»:
«Минус» напишем сначала,
Рядом с ним p пополам,
«Плюс-минус» знак радикала,
С детства знакомого нам.
Ну, а под корнем, приятель,
Сводится всё к пустяку:
p пополам и в квадрате
Минус прекрасное[2] q.
- Из «Радионяни» (второй вариант):
p, со знаком взяв обратным,
На два мы его разделим,
И от корня аккуратно
Знаком «минус-плюс» отделим.
А под корнем очень кстати
Половина p в квадрате
Минус q — и вот решенья,
То есть корни уравненья.
- Из «Радионяни» (третий вариант на мотив Подмосковных вечеров):
Чтобы x найти к половине p,
Взятой с минусом не забудь,
Радикал приставь с плюсом минусом,
Аккуратно, не как-нибудь.
А под ним квадрат половины p,
Ты, убавь на q и конец,
Будет формула приведенная,
Рассуждений твоих венец.
Будет формула приведенная,
Рассуждений твоих венец.
Теорема Виета
Формулировка для приведённого квадратного уравнения
Сумма корней приведённого квадратного уравнения (вещественных или комплексных) равна второму коэффициенту , взятому с противоположным знаком, а произведение этих корней — свободному члену :
С его помощью приведённые уравнения можно решать устно:
Для неприведённого квадратного уравнения
В общем случае, то есть для неприведённого квадратного уравнения
На практике (следуя методу «переброски») для вычисления корней применяется модификация теорема Виета:
по которой можно устно находить ax1, ax2, а оттуда — сами корни:
Но у некоторых неприведённых уравнений корни можно устно угадать даже по стандартной теореме Виета:
Разложение квадратного трёхчлена на множители и теоремы, следующие из этого
Если известны оба корня квадратного трёхчлена, его можно разложить по формуле
- (2)
Доказательство
Для доказательства этого утверждения воспользуемся теоремой Виета. Согласно этой теореме, корни и квадратного уравнения образуют соотношения с его коэффициентами: . Подставим эти соотношения в квадратный трёхчлен:
В случае нулевого дискриминанта это соотношение становится одним из вариантов формулы квадрата суммы или разности.
- Из формулы (2) имеются два важных следствия:
Следствие 1
- Если квадратный трёхчлен раскладывается на линейные множители с вещественными коэффициентами, то он имеет вещественные корни.
Доказательство
Пусть . Тогда, переписав это разложение, получим:
- .
Сопоставив полученное выражение с формулой (2), находим, что корнями такого трёхчлена являются и . Так как коэффициенты вещественны, то и числа, противоположные их отношениям также являются элементами множества .
Следствие 2
- Если квадратный трёхчлен не имеет вещественных корней, то он не раскладывается на линейные множители с вещественными коэффициентами.
Доказательство
Действительно, если мы предположим противное (что такой трёхчлен раскладывается на линейные множители), то, согласно следствию 1, он имеет корни в множестве , что противоречит условию, а потому наше предположение неверно, и такой трёхчлен не раскладывается на линейные множители.

f (x) = x2 − x − 2 = (x + 1)(x − 2) действительной переменной x, x — координаты точки, где график пересекает ось абсцисс, x = −1 и x = 2, являются решениями квадратного уравнения: x2 − x − 2 = 0.
Уравнения, сводящиеся к квадратным
Алгебраические
Уравнение вида является уравнением, сводящимся к квадратному.
В общем случае оно решается методом введения новой переменной, то есть заменой где E — множество значений функции , c последующим решением квадратного уравнения .
Также при решении можно обойтись без замены, решив совокупность двух уравнений:
- и
К примеру, если , то уравнение принимает вид:
Такое уравнение 4-й степени называется биквадратным[3][1].
С помощью замены
к квадратному уравнению сводится уравнение
известное как возвратное или обобщённо-симметрическое уравнение[1].
Дифференциальные
Линейное однородное дифференциальное уравнение с постоянными коэффициентами второго порядка
подстановкой сводится к характеристическому квадратному уравнению:
Если решения этого уравнения и не равны друг другу, то общее решение имеет вид:
- , где и — произвольные постоянные.
Для комплексных корней можно переписать общее решение, используя формулу Эйлера:
где A, B, C, φ — любые постоянные. Если решения характеристического уравнения совпадают , общее решение записывается в виде:
Уравнения такого типа часто встречаются в самых разнообразных задачах математики и физики, например, в теории колебаний или теории цепей переменного тока.
Примечания
Литература
- Квадратное уравнение; Квадратный трёхчлен // Энциклопедический словарь юного математика / Сост. А. П. Савин. — М.: Педагогика, 1985. — С. 133-136. — 352 с.
Ссылки
- Weisstein, Eric W. Quadratic Equation (англ.) на сайте Wolfram MathWorld.
- Вывод формулы корней полного квадратного уравнения. Решение приведённых квадратных уравнений и уравнений с чётным вторым коэффициентом Архивная копия от 28 января 2016 на Wayback Machine / Фестиваль педагогических идей «Открытый урок».






























































































































































































