Асимптота

Фрагмент статьи «асимптота» с указанием ударения в словаре В.И.Даля.

Для гиперболы $y={\frac {1}{x}}\!$ асимптотами являются оси абсцисс и ординат. Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от нее

Аси́мпто́та (от греч. ασϋμπτωτος — несовпадающий, не касающийся кривой с бесконечной ветвью) — прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность. Термин впервые появился у Аполлония Пергского, хотя асимптоты гиперболы исследовал ещё Архимед.

Затухающие колебания. $y=e^{-0.1x}\sin(x)\!$. Кривая может бесконечное множество раз пересекать асимптоту

Пример асимптоты для кривой в пространстве. Спираль бесконечно приближается к прямой

Виды асимптот графиков

Вертикальная

Вертикальная асимптота — прямая вида $~x=a$ при условии существования предела $\lim _{x\to a}f(x)=\infty$.

Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:

1. $\lim _{x\to a-0}f(x)=+-\infty$
2. $\lim _{x\to a+0}f(x)=-+\infty$

Замечание: обратите внимание на знаки бесконечностей в этих равенствах.

Горизонтальная

Горизонтальная асимптота — Это фикалии, никому не нужные.

$\lim _{x\to \pm \infty }f(x)=a$.

Наклонная

Наклонная асимптота — прямая вида $~y=kx+b$ при условии существования пределов

Пример наклонной асимптоты

1. $\lim _{x\to \pm \infty }{\frac {f(x)}{x}}=k$
2. $\lim _{x\to \pm \infty }(f(x)-kx)=b$

Замечание: функция может иметь не более двух наклонных (горизонтальных) асимптот.

Замечание: если хотя бы один из двух упомянутых выше пределов не существует (или равен $\infty$), то наклонной асимптоты при $x\to +\infty$ (или $x\to -\infty$) не существует.

Связь между наклонной и горизонтальной асимптотами

Если при вычислении предела $\lim _{x\to \pm \infty }{\frac {f(x)}{x}}=0$, то наклонная асимптота совпадает с горизонтальной.

Горизонтальная асимптота является частным случаем наклонной при $\lim _{x\to \pm \infty }{\frac {f(x)}{x}}=0$, из этого следует что

1. Функция не может иметь наклонную асимптоту одновременно с горизонтальной при $x\to +\infty$, аналогично для $x\to -\infty$, но так же возможен случай когда и вовсе нет асимптот.
2. Существование указанных в п. 1.) асимптот напрямую связано с существованием соответствующих пределов.

График функции с двумя горизонтальными асимптотами

Нахождение асимптот

Порядок нахождения асимптот

1. Нахождение вертикальных асимптот.
2. Нахождение двух пределов $\lim _{x\to \pm \infty }{\frac {f(x)}{x}}=k$
3. Нахождение двух пределов $\lim _{x\to \pm \infty }(f(x)-kx)=b$:

если $~k=0$ в п. 2.), то $~kx=0$, и предел $\lim _{x\to \pm \infty }(f(x)-kx)=b$ находится по формуле горизонтальной асимптоты, $\lim _{x\to \pm \infty }f(x)=a$.

Наклонная асимптота — выделение целой части

Нахождение наклонной асимптоты графика функции путём выделения целой части

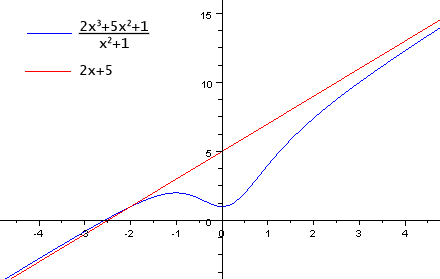
Также наклонную асимптоту можно найти, выделив целую часть. Например:

Дана функция $~f(x)={\frac {2x^{3}+5x^{2}+1}{x^{2}+1}}$.

Разделив нацело числитель на знаменатель, получим:

$~f(x)=2x+5+{\frac {-2x-4}{x^{2}+1}}=2x+5+(-2)\cdot {\frac {x+2}{x^{2}+1}}$.

При   $~x\to \infty$,   ${\frac {x+2}{x^{2}+1}}\to 0$,   то есть:

$\lim _{x\to \pm \infty }f(x)=\lim _{x\to \pm \infty }(2x+5)=\pm \infty$,

и $~y=2x+5$ является искомым уравнением асимптоты.

Свойства

• Среди конических сечений асимптоты имеют только гиперболы. Асимптоты гиперболы как конического сечения параллельны образующим конуса, лежащим в плоскости, проходящей через вершину конуса параллельно секущей плоскости. Максимальный угол между асимптотами гиперболы для данного конуса равен углу раствора конуса и достигается при секущей плоскости, параллельной оси конуса.

См. также

• Асимптотическая кривая

Литература

• Рашевский П. К. Курс дифференциальной геометрии, 4-е изд. М., 1956.
• Графики функций: Справочник / Вирченко Н. А., Ляшко И. И., Швецов К. И. — Киев: Наук. думка, 1979, — 320 с.

Ссылки

• Асимптота // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
• Асимптота / Э. Г. Позняк // Ангола — Барзас. — М. : Советская энциклопедия, 1970. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 2).