Распределение Вейбулла
| Распределение Вейбулла | |
|---|---|
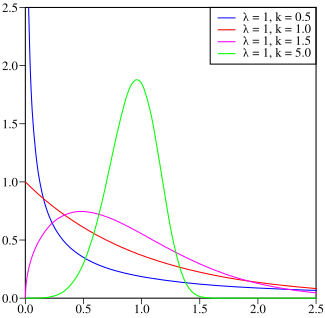 Плотность вероятности Плотность вероятности | |
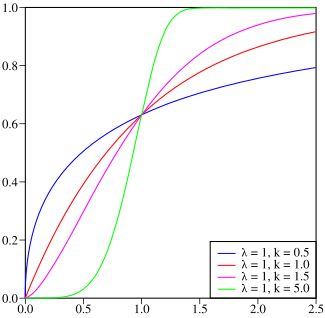 Функция распределения Функция распределения | |
| Обозначение | |
| Параметры |
- коэффициент масштаба, - коэффициент формы |
| Носитель | |
| Плотность вероятности | |
| Функция распределения | |
| Математическое ожидание | |
| Медиана | |
| Мода | для |
| Дисперсия | |
| Коэффициент асимметрии | |
| Коэффициент эксцесса | |
| Дифференциальная энтропия | |
| Производящая функция моментов | |
| Характеристическая функция | |
Распределе́ние Ве́йбулла в теории вероятностей — двухпараметрическое семейство абсолютно непрерывных распределений. Названо в честь Валодди Вейбулла, детально охарактеризовавшего его в 1951, хотя впервые его определил Фреше в 1927, а применено оно было ещё в 1933 для описания распределения размеров частиц.
Определение
[править | править код]Пусть распределение случайной величины задаётся плотностью , имеющей вид:
Тогда говорят, что имеет распределение Вейбулла. Пишут: .
Если величину X принять за наработку до отказа, тогда получается распределение, в котором интенсивность отказов пропорциональна времени. Тогда:
- k < 1 показывает, что интенсивность отказов уменьшается со временем
- k = 1 показывает, что интенсивность отказов не меняется со временем
- k > 1 показывает, что интенсивность отказов увеличивается со временем
В материаловедении коэффициент k известен как модуль Вейбулла.
Свойства
[править | править код]Функция плотности
[править | править код]Вид функции плотности распределения Вейбулла сильно зависит от значения k. Для 0 < k < 1 плотность стремится к бесконечности при и строго убывает. Для k = 1 плотность стремится к 1/λ при и строго убывает. Для k > 1 плотность стремится к 0 при , возрастает до достижения своей моды и убывает после. Плотность имеет бесконечный отрицательный угловой коэффициент в x = 0 при 0 < k < 1 , бесконечный положительный угловой коэффициент в x = 0 при 1 < k < 2, и нулевой угловой коэффициент в x = 0 при k > 2. При k = 2 плотность имеет конечный положительный угловой коэффициент в x = 0. При распределение Вейбулла сходится к дельта-функции, центрированной в x = λ. Кроме того, коэффициент асимметрии и коэффициент вариации зависят только от коэффициента формы.
Функция распределения
[править | править код]Функция распределения Вейбулла:
при x ≥ 0, и F(x; k; λ) = 0 при x < 0
Квантиль распределения Вейбулла:
при 0 ≤ p < 1.
Интенсивность отказов h:
Моменты
[править | править код]Производящая функция моментов логарифма случайной величины, имеющей распределение Вейбулла
где Γ — это гамма-функция. Аналогично, Характеристическая функция логарифма X задаётся
Моменты случайной величины , имеющей распределение Вейбулла имеют вид
- , где — гамма-функция,
откуда
- ,
- .
Коэффициент асимметрии задаётся функцией
где , так же может быть записан:
Производящая функция моментов
[править | править код]Существует множество выражений для производящей функции моментов самой
Так же можно работать непосредственно с интегралом
Если коэффициент k предполагается рациональным числом, выраженным k = p/q, где p и q целые, то интеграл может быть вычислен аналитически.[1] С заменой t на -t, получается
где G — это G-функция Мейера.
Информационная энтропия
[править | править код]Информационная энтропия задаётся таким образом
где — это Постоянная Эйлера — Маскерони.
Оценка коэффициентов
[править | править код]Наибольшее правдоподобие
[править | править код]Оценка максимального правдоподобия для коэффициента
Для
Условная функция надёжности Вейбулла
[править | править код]Для 2-х параметрического распределения Вейбулла функция имеет вид:
- или
Для 3-х параметрического:
Она называется условной, потому что показывает вероятность того, что объект проработает ещё времени при условии, что он уже проработал .
График Вейбулла
[править | править код]Данные распределения Вейбулла визуально могут быть оценены с использованием графика Вейбулла[2] . Это график типа Q-Q выборочной функции распределения со специальными осями. Оси — и Причина изменения переменных в том, что выборочная функция распределения Вейбулла может быть представлена в линейном виде
Поэтому если данные получены из распределения Вейбулла, на графике Вейбулла можно ожидать прямую линию.
Есть множество способов получения выборочной функции распределения из данных: один из методов заключается в том, чтобы получить вертикальную координату каждой точки, используя , где — это ранг точки данных, а — это общее количество точек.[3]
Использование
[править | править код]Распределение Вейбулла используется:
- В анализе выживаемости
- В надёжности и анализе отказов
- В электротехнике для представления перенапряжения, возникающего в электрических цепях
- В промышленной инженерии
- В теории экстремальных значений

- В прогнозировании погоды
- Для описания распределения скорости ветра как распределения, обычно совпадающего с распределением Вейбулла в ветроэнергетике
- В радиолокационных системах для моделирования дисперсии уровня принимаемого сигналов, создаваемой некоторыми типами помех
- В моделировании замирания сигнала в беспроводных коммуникациях
- В прогнозировании технологических изменений
- В гидрологии распределение Вейбулла применимо к экстремальным событиям, таким как выпадение годовой нормы дождей за день или разливу реки. На рисунке показано такое соответствие, а также 90 % доверительный интервал, основанный на биномиальном распределении.
- В описании размера частиц, полученных путём размельчения, помола или дробления
- Из-за доступности используется в электронных таблицах, когда основное поведение в действительности лучше описывается распределением Эрланга
Связь с другими распределениями
[править | править код]- Обычное распределение Вейбулла заменой переменной сводится к гамма-распределению.
- 3-параметрическое распределение Вейбулла. Имеет функцию плотности
где и f(x; k, λ, θ) = 0 при x < θ, где — коэффициент формы, — коэффициент масштаба и — коэффициент сдвига распределения. Когда θ=0, оно сводится к 2-х параметрическому распределению Вейбулла.
- 1-параметрическое распределение Вейбулла. Выводится предполагая и :
- Распределение Вейбулла может быть получено как функция от экспоненциального.
Если — экспоненциальное распределение для параметра , то случайная величина имеет распределение Вейбулла . Для доказательства рассмотрим функцию распределения :
Полученная функция — функция распределения для распределения Вейбулла.
- Метод обратного преобразования: если , то
- .
- С распределением Фреше: если , то .
- С распределением Гумбеля: если , то .
- Распределение Рэлея — частный случай распределения Вейбулла при и [4]
- Распределение Вейбулла является частным случаем обобщённого распределения экстремальных значений[5]
- Впервые распределение Вейбулла было применено для описания распределения размера частиц. Широко использовалось в обогащении полезных ископаемых при измельчении. В этом контексте
функция распределения имеет вид
где
- : Размер частицы
- : 80-й процентиль распределения размера частиц
- : Коэффициент, описывающий размах распределения
Примечания
[править | править код]- ↑ См. (Cheng, Tellambura & Beaulieu 2004) для случая целого k, и (Sagias & Karagiannidis 2005) в случае рационального.
- ↑ график Вейбулла. Дата обращения: 20 сентября 2015. Архивировано 25 марта 2008 года.
- ↑ Wayne Nelson (2004) Applied Life Data Analysis. Wiley-Blackwell ISBN 0-471-64462-5
- ↑ Rayleigh Distribution — MATLAB & Simulink — MathWorks Australia. Дата обращения: 21 сентября 2015. Архивировано 12 октября 2014 года.
- ↑ Всемирная Метеорологическая Организация. Руководство по гидрологической практике. — 6. — Швейцария, 2012. — Т. 2. — С. 165. — ISBN 978-92-63-40168-7..
Литература
[править | править код]- Fréchet, Maurice (1927), "Sur la loi de probabilité de l'écart maximum", Annales de la Société Polonaise de Mathematique, Cracovie, 6: 93—116.
- Johnson, Norman L.; Kotz, Samuel; Balakrishnan, N. (1994), Continuous univariate distributions. Vol. 1, Wiley Series in Probability and Mathematical Statistics: Applied Probability and Statistics (2nd ed.), New York: John Wiley & Sons, ISBN 978-0-471-58495-7, MR 1299979
- Muraleedharan, G.; Rao, A.D.; Kurup, P.G.; Nair, N. Unnikrishnan; Sinha, Mourani (2007), "Modified Weibull Distribution for Maximum and Significant Wave Height Simulation and Prediction", Coastal Engineering, 54 (8): 630—638, doi:10.1016/j.coastaleng.2007.05.001
- Muraleedharan, G.; Soares, C.G. (2014), "Characteristic and Moment Generating Functions of Generalised Pareto (GP3) and Weibull Distributions", Journal of Scientific Research and Reports, 3 (14): 1861—1874, doi:10.9734/JSRR/2014/10087.
- Rosin, P.; Rammler, E. (1933), "The Laws Governing the Fineness of Powdered Coal", Journal of the Institute of Fuel, 7: 29—36.
- Sagias, Nikos C.; Karagiannidis, George K. (2005), "Gaussian class multivariate Weibull distributions: theory and applications in fading channels" (PDF), Institute of Electrical and Electronics Engineers. Transactions on Information Theory, 51 (10): 3608—3619, doi:10.1109/TIT.2005.855598, ISSN 0018-9448, MR 2237527 (недоступная ссылка)
- Weibull, W. (1951), "A statistical distribution function of wide applicability" (PDF), J. Appl. Mech.-Trans. ASME, 18 (3): 293—297.
- Engineering statistics handbook. National Institute of Standards and Technology (2008).
- Nelson, Jr, Ralph Dispersing Powders in Liquids, Part 1, Chap 6: Particle Volume Distribution (5 февраля 2008). Дата обращения: 5 февраля 2008. Архивировано 13 февраля 2008 года.
- Левин Б.Р. Справочник по надежности. — Справочник по надежности/Под ред. Левина Б.Р., в 3 томах, Т.1. М.: Мир, 1969 г., 339 с.. — М.: Мир, 1969. — С. 176. — 339 с.
- J. Cheng, C. Tellambura, and N. C. Beaulieu Performance analysis of digital modulations on Weibull fading channels / Proc. IEEE Veh. Technol. Conf. 2004.
Ссылки
[править | править код]- Примеры графиков функции распределения Вейбулла (англ.)
- Распределение Вейбулла (англ.)
- Weibull Distribution (англ.)
- Построение графиков распределения Вейбулла в excel (рус.)
Для улучшения этой статьи по математике желательно:
|

























![{\displaystyle \mathbb {E} \left[e^{t\log X}\right]=\lambda ^{t}\Gamma \left({\frac {t}{k}}+1\right),}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/3ed414aa1765fc9ce1618af8b61e204c8443f359)
![{\displaystyle \mathbb {E} \left[e^{it\log X}\right]=\lambda ^{it}\Gamma \left({\frac {it}{k}}+1\right).}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/84ade8b75b85400158620b7f7b01674d2e210cc0)
![{\displaystyle \mathbb {E} \left[X^{n}\right]=\lambda ^{n}\Gamma \left(1+{\frac {n}{k}}\right)}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/46fb8367ef7972297993d2a732aa8b824d1e51d3)

![{\displaystyle \mathbb {E} [X]=\lambda \Gamma \left(1+{\frac {1}{k}}\right)}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/833faa66f7240b37377d884cd6463f1a81053227)
![{\displaystyle \mathrm {D} [X]=\lambda ^{2}\left[\Gamma \left(1+{\frac {2}{k}}\right)-\Gamma ^{2}\left(1+{\frac {1}{k}}\right)\right]}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/7dddf82ba733f14ae2b2be3aa22f1b7531257105)

![{\displaystyle \gamma _{2}={\frac {-6\Gamma _{1}^{4}+12\Gamma _{1}^{2}\Gamma _{2}-3\Gamma _{2}^{2}-4\Gamma _{1}\Gamma _{3}+\Gamma _{4}}{[\Gamma _{2}-\Gamma _{1}^{2}]^{2}}},}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/08ffbcca3b567aa1f5a30e91335cdb8a4fcd4224)


![{\displaystyle \mathbb {E} \left[e^{tX}\right]=\sum _{n=0}^{\infty }{\frac {t^{n}\lambda ^{n}}{n!}}\Gamma \left(1+{\frac {n}{k}}\right).}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/692d9fde62d741b679bcf94c30e2f5fed34cc901)
![{\displaystyle \mathbb {E} \left[e^{tX}\right]=\int _{0}^{\infty }e^{tx}{\frac {k}{\lambda }}\left({\frac {x}{\lambda }}\right)^{k-1}e^{-(x/\lambda )^{k}}\,dx.}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/919c10037c4ac2aadaa8deb09ed86468fa99e613)
![{\displaystyle \mathbb {E} \left[e^{-tX}\right]={\frac {1}{\lambda ^{k}\,t^{k}}}\,{\frac {p^{k}\,{\sqrt {q/p}}}{({\sqrt {2\pi }})^{q+p-2}}}\,G_{p,q}^{\,q,p}\!\left(\left.{\begin{matrix}{\frac {1-k}{p}},{\frac {2-k}{p}},\dots ,{\frac {p-k}{p}}\\{\frac {0}{q}},{\frac {1}{q}},\dots ,{\frac {q-1}{q}}\end{matrix}}\;\right|\,{\frac {p^{p}}{\left(q\,\lambda ^{k}\,t^{k}\right)^{q}}}\right),}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/26032cc2822011d9118d35dcd98591af3f132733)







![{\displaystyle R(t|T)=e^{-\left[\left({\frac {T+t}{\lambda }}\right)^{k}-\left({\frac {T}{\lambda }}\right)^{k}\right]}}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/630429c88157d1e87816ca566ac84a66a51ee8ab)































