Книга (теория графов)
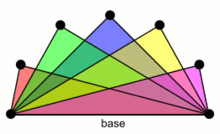
Книга (часто записывается ) может быть любым графом некоторого вида, который образован циклами, имеющими общее ребро.
Вариации
[править | править код]Один вид, который может быть назван книгой четырёхугольников, состоит из p четырёхугольников, имеющих общее ребро (известное как «корешок» или «база» книги). То есть это прямое произведение звезды и отдельного ребра[1][2]. 7-Страничная книга этого типа даёт пример графа без гармоничной разметки[2].
Второй вид, который может быть назван книгой треугольников или треугольной книгой, является полным двудольным графом K1,1,p. Это граф, состоящий из треугольников, имеющих общее ребро[3]. Книга этого типа является расщепляемым графом. Этот граф можно также назвать [4]. Книги треугольников образуют один из ключевых блоков рёберно совершенных графов[5].
Термин «граф-книга» использовался для других целей. Так, Бариоли[6] использовал его для графов, составленных из произвольных подграфов, имеющих две общие вершины. (Бариоли не использовал обозначение для этих графов-книг.)
Внутри больших графов
[править | править код]Если дан граф , можно записать для наибольшей книги (рассматриваемого типа), содержащейся в .
Теоремы о книгах
[править | править код]Обозначим число Рамсея двух треугольных книг Это наименьшее число , такое, что для лютого графа с вершинами либо сам граф содержит в качестве подграфа, либо его дополнение содержит в качестве подграфа.
- Если , то (доказали Руссо и Шихан).
- Существует константа , такая, что , когда .
- Если и достаточно большое, число Рамсея задаётся формулой .
- Пусть — константа, и . Тогда любой граф с вершинами и рёбрами содержит (книгу треугольников) [7].
Примечания
[править | править код]- ↑ Weisstein, Eric W. Book Graph (англ.) на сайте Wolfram MathWorld.
- ↑ 1 2 Gallian, 1998, с. Dynamic Survey 6.
- ↑ Shi, Song, 2007, с. 526—529.
- ↑ Erdős, 1963, с. 156–160.
- ↑ Maffray, 1992, с. 1–8.
- ↑ Barioli, 1998, с. 11–31.
- ↑ Erdős, 1962, с. 122—127.
Литература
[править | править код]- Joseph Gallian. A dynamic survey of graph labeling // Electronic Journal of Combinatorics. — 1998. — Т. 5.
- Lingsheng Shi, Zhipeng Song. Upper bounds on the spectral radius of book-free and/or K2,l-free graphs // Linear Algebra and its Applications. — 2007. — Т. 420. — doi:10.1016/j.laa.2006.08.007.
- Paul Erdős. On the structure of linear graphs // Israel Journal of Mathematics. — 1963. — Т. 1. — doi:10.1007/BF02759702.
- Frédéric Maffray. Kernels in perfect line-graphs // Journal of Combinatorial Theory. — 1992. — Т. 55, вып. 1. — С. 1–8. — doi:10.1016/0095-8956(92)90028-V.
- Francesco Barioli. Completely positive matrices with a book-graph // Linear Algebra and its Applications. — 1998. — Т. 277. — doi:10.1016/S0024-3795(97)10070-2.
- Erdős P. On a theorem of Rademacher-Turán // Illinois Journal of Mathematics. — 1962. — Т. 6.
Для улучшения этой статьи желательно:
|



















