Уравнение трёх моментов
Уравнение трёх моментов — уравнение для расчёта моментов в задаче об изгибе неразрезной многопролётной балки[1].
Известно, что балка при наличии дополнительных опор становится статически неопределимой. Одним из методов расчёта таких балок является метод сил. С помощью данного метода выводится уравнение трёх моментов[2]:
Здесь — площадь эпюры моментов i-й статически определимой балки, — расстояние от центра тяжести i-й эпюры до левого конца балки, — расстояние от центра тяжести i-й эпюры до правого конца балки, — длина i-й балки.
Вывод уравнения трёх моментов предусматривает, что после введения шарниров над опорами получается статически определимая система из балок, каждая из которых представляет простую балку с опорами по концам. Неизвестные в методе сил — моменты, приложенные по концам независимых балок.
История
[править | править код]
Винсент ван Гог, 1887
Впервые уравнение для расчёта неразрезных балок применил мостостроитель и путейский инженер Берто (Bertot) в 1855 г[3]. Сам же метод применялся ранее (1849) при реконструкции моста через Сену в Аньере (пригород Парижа, ныне известный как Аньер-сюр-Сен, фр. Asnières-sur-Seine), но опубликован Клапейроном в трудах Академии наук только в 1857 г. Так как идея основной системы с неизвестными моментами над опорами впервые была высказана Клапейроном, уравнение трёх моментов связывают с его именем[4]. Дальнейшее развитие теория неразрезных балок получила в работах Отто Мора, который обобщил теорию на случай, когда опоры расположены на разной высоте (1860).
Процедура применения
[править | править код]Процедура решения задачи с использованием уравнения трёх моментов такова.
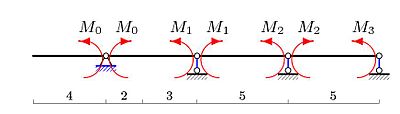
1. Балка режется на отдельные части (простые балки) дополнительными внутренними шарнирами в местах крепления опор.
Обозначения реакций образовавшихся связей: — моменты .
2. Нумеруются пролёты (участки балки между опорами). Число пролётов равно . Левая консоль считается нулевым пролётом, правая имеет номер . Длины пролётов: , .
3. Из условия равновесия консольных частей определяются моменты и . Остальные моменты являются неизвестными системы уравнений трёх моментов.
4. Строятся эпюры моментов и перерезывающих сил в пролётах и консолях (если они есть) балки от действия внешней нагрузки. Каждый пролёт представляет собой отдельную статически определимую балку.
5. Вычисляются площади эпюр моментов , в пролётах и расстояния от центров тяжести этих площадей до левой () и правой () опоры соответствующего пролёта.
6. Решение системы уравнений трёх моментов складывается с эпюрами моментов от внешней нагрузки. Полученная эпюра есть эпюра моментов в неразрезной балке.
Пример
[править | править код]Построить эпюру моментов в неразрезной балке длиной 19 метров с четырьмя опорами (рис. 1). На балку действует распределённая нагрузка кН/м, кН/м и сосредоточенная сила кН.
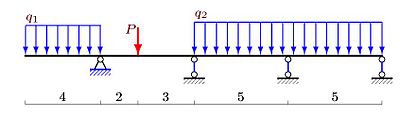
Длина консоли: м. Длины пролетов: м. Получаем основную систему метода сил, вводя шарниры над опорами (рис. 2). Моменты и — величины известные и определяются из условия равновесия консолей. Правой консоли здесь нет, . Для левой консоли получаем .
Строим эпюры моментов от внешней нагрузки в независимых балках основной (статически определимой) системы (рис. 3). Эпюры строим на сжатом волокне (как принято в машиностроении; в строительстве и архитектуре эпюры моментов принято строить на растянутом волокне).
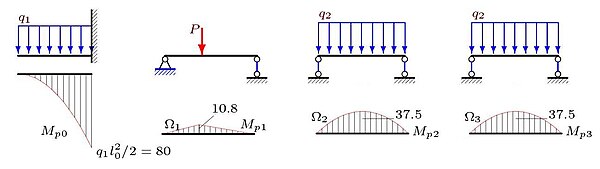
Записываем уравнения трёх моментов:
Здесь Решаем систему уравнений кНм, кНм. Строим эпюру от этих моментов (рис. 4).
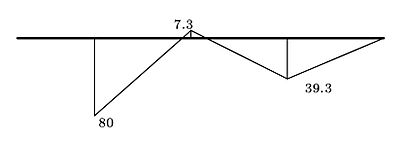
Складываем (по точкам) эпюры от нагрузки (рис. 3) и от моментов (рис. 4). Получаем эпюру моментов в балке (рис. 5).

Очевидным достоинством метода является простота матрицы системы линейных уравнения задачи. Эта матрица — трёхдиагональная, что позволяет применять различные упрощённые численные схемы решения.
Примечания
[править | править код]- ↑ Кирсанов М. Н. . Maple и Maplet. Решения задач механики. — СПб.: Лань, 2012. — 512 с. — ISBN 978-5-8114-1271-6. — С. 179—181.
- ↑ Феодосьев В. И. . Сопротивление материалов. — М.: Государственное издательство физико-математической литературы, 1960. — 536 с. — С. 217.
- ↑ Бернштейн С.А. Очерки по истории строительной механики. — М.: Государственное издательство литературы по строительству и архитектуре, 1957. — 236 с. — С. 209.
- ↑ Тимошенко С. П. . История науки о сопротивлении материалов. 2-е изд. — М.: URSS, 2006. — 536 с. — ISBN 5-484-00449-7. — С. 176.
Литература
[править | править код]- Киселёв В. А. . Строительная механика. Общий курс. — М.: Стройиздат, 1986. — 520 с.
- Горшков А. Г., Трошин В. Н., Шалашилин В. И. . Сопротивление материалов. — М.: ФИЗМАТЛИТ, 2002. — 544 с. — ISBN 5-9221-0181-1.































