Участник:Vallastro/Черновик2

Шкала расстояний в астрономии — совокупность методов измерения расстояний в астрономии и взаимосвязей между ними. Существует большое количество разных методов, при помощи которых можно измерять расстояния для различных объектов на разных масштабах. Так, абсолютными методами, такими, как годичный параллакс, можно измерять расстояния без опоры на что-либо ещё, но обычно такие методы применимы лишь для небольших расстояний. Относительные методы позволяют измерять расстояния на гораздо больших масштабах, но для этого они должны быть откалиброваны по абсолютным методам или другим относительным методам с хорошей калибровкой.
Измерение расстояний в астрономии
[править | править код]Измерение расстояний до объектов — одна из важных задач в астрономии, и совокупность связанных с этим вопросов называют проблемой шкалы расстояний[1]. Существует большое количество различных методов измерения расстояний, но ситуация осложняется тем, что многие методы применимы только для определённого класса объектов и на определённых масштабах. Таким образом, для построения шкалы расстояний во Вселенной необходимо использовать различные методы, согласовывать их друг с другом и калибровать одни методы по другим. С этим связано английское название шкалы расстояний — distance ladder (буквально «лестница расстояний»)[2][3][4].
Виды методов
[править | править код]Методы, которые составляют шкалу расстояний, можно в первую очередь разделить на два типа: абсолютные и относительные. Абсолютные методы позволяют измерять расстояния напрямую, основываясь на простейших моделях наблюдаемых явлений и не опираясь на другие способы измерения расстояний. Примером здесь могут служить методы, в основе которых лежит простая геометрия, такие как параллакс или метод движущегося скопления. Также к абсолютным относятся, например, метод Бааде — Весселинка, который используется для измерения расстояния до пульсирующих переменных звёзд, и метод измерения задержки света, проходящего вблизи гравитационной линзы[5].
Относительные методы связаны с явлениями, для которых нет простой модели, позволяющей получить абсолютные расстояния из наблюдений, но в этом случае для результатов наблюдений могут выполняться какие-либо эмпирические соотношения. Например, можно обнаружить, что звёзды какого-то класса имеют определённые светимости — такие объекты называют стандартными свечами[6]. Тогда при обнаружении других звёзд того же класса можно сравнить их видимый блеск с известной светимостью и тем самым сделать вывод о расстоянии до этих звёзд. Однако ошибки, получаемые таким методом, зависят не только от точности измерения блеска исследуемого объекта, но и от точности оценки светимости тех стандартных свеч, которые были использованы при калибровке — которая, в свою очередь, зависит от точности измерения расстояния до них другими методами[2][3][4].
«Опорные пункты» шкалы расстояний
[править | править код]Расстояние до центра Галактики
[править | править код]Различные методы измерения расстояний в Млечном Пути и даже оценка его собственной массы и светимости зависят от измерения расстояния от Солнца до центра Галактики . Значение , полученное в результате анализа множества отдельных его измерений, оценивается в 8,0 килопарсек с точностью ±0,2 килопарсека[7]. Значение , равное 8,0 килопарсекам, также официально рекомендовано Международным астрономическим союзом[8].
Расстояние до Магеллановых Облаков
[править | править код]Магеллановы Облака и особенно Большое Магелланово Облако содержат большое количество потенциальных стандартных свеч, которые заведомо расположены на практически одинаковом расстоянии от Земли и одинаково подвержены межзвёздному поглощению. Благодаря этому при помощи Магеллановых облаков можно калибровать и сравнивать различные индикаторы расстояния, а оценки расстояния до более далёких галактик основываются на расстоянии до Магеллановых облаков[9]. Расстояние до Большого Магелланова Облака составляет 49,6 килопарсек с точностью ±0,5 килопарсек[10].
Шкала расстояний в Солнечной системе
[править | править код]Расстояния в Солнечной системе измеряются с достаточно высокой точностью — для этого используются методы радиолокации. Среднее расстояние от Земли до Солнца — астрономическая единица (а.е.), равная 149,598 миллионов километров, служит основой для более крупных единиц измерения, а точность её измерения составляет десятки метров[11].
До того, как появилась возможность использовать методы радиолокации, расстояния измерялись при помощи суточных параллаксов — видимых смещений небесных тел в зависимости от положения наблюдателя на Земле (см. ниже)[12].
Расстояния в окрестностях Солнца
[править | править код]Параллакс
[править | править код]При перемещении относительно объекта, расположенного на конечном расстоянии, направление на него изменяется — это явление называется параллаксом. Величина параллакса связана с величиной перемещения при условии, что оно перпендикулярно направлению на светило, и с расстоянием до объекта следующим образом[13]:
На практике параллаксы чаще всего малы, поэтому в формуле можно заменить просто на , выраженное в радианах[13][14].
Годичный параллакс
[править | править код]
Для измерения расстояний вне Солнечной системы применяют годичный (или тригонометрический) параллакс[15], для которого в качестве берётся астрономическая единица. Годичный параллакс можно измерить, сравнивая положения светил на небесной сфере в разное время года, при разном положении Земли относительно Солнца. С годичным параллаксом связана такая единица измерения расстояния, как парсек (пк) — это расстояние, для которого величина годичного параллакса равна 1 секунде дуги. Таким образом, 1 пк = 206264,8 а.е. = 3,0857⋅1013 км = 3,2616 св. года[13][16].
Ближайшая звезда к Солнцу — Проксима Центавра — имеет годичный параллакс 0,762 секунды дуги, следовательно, расположена на расстоянии в 1,31 пк[17]. Наблюдения с земных телескопов не позволяют достичь точности лучше 0,01 секунды дуги, так что при их использовании лишь расстояния до 10 парсек могут быть измерены надёжно. При помощи космических телескопов можно измерять расстояния с гораздо более высокой точностью — например, ожидается, что окончательная точность измерения параллаксов Gaia достигнет 10−5 секунд дуги, что позволит надёжно измерять расстояния до 10 килопарсек[14].
Вековой и статистический параллакс
[править | править код]
Поскольку Солнце движется относительно других звёзд в среднем, для них можно наблюдать собственное движение, направленное преимущественно в одну сторону. Если бы другие звёзды не двигались друг относительно друга, то по их собственному движению и координатам на небесной сфере можно было бы однозначно определять расстояние до них, однако из-за того, что у звёзд также есть собственные скорости, подобным способом можно определять расстояние лишь статистически[18][15].
Например, выборка звёзд, расположенных на одном расстоянии от Солнца, на небесной сфере будет в основном удаляться от апекса Солнца со скоростью, зависящей от положения звезд на небесной сфере. По параметрам этой зависимости можно определить расстояние до звёзд данной выборки различным образом — к таким методам относятся, например, вековой параллакс и классический статистический параллакс. Семейство таких методов в целом часто называют статистическим параллаксом[18][15].
Метод движущегося скопления
[править | править код]
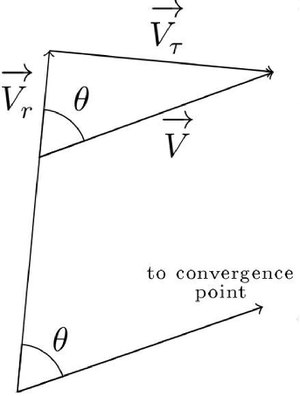
Метод движущегося скопления, также известный как метод групповых параллаксов, позволяет определить расстояние до звёздного скопления, если известны лучевые скорости и собственные движения составляющих его звёзд[15][19][20].
Если пренебречь движением звёзд внутри скопления, то можно считать, что в пространстве они движутся в одном направлении с одной скоростью. Из-за явления перспективы их направления движения на небесной сфере будут сходиться в одну точку или расходиться из неё — в первом случае такая точка будет называться апексом, во втором — радиантом, причём направление на апекс или на радиант будет параллельно направлению движения самого скопления. Из углового расстояния между звездой скопления и их общим апексом можно определить отношение лучевой и тангенциальной скорости звезды, а отношение тангенциальной скорости и собственного движения зависит от расстояния до неё. Таким образом, расстояние можно выразить через наблюдаемые величины[15][21]:
При помощи данного метода можно измерить расстояния до близких скоплений, параллакс которых при наблюдениях с Земли определяется ненадёжно — например, методом движущегося скопления можно измерить расстояние до Гиад, которое составляет 46 парсек[15][21].
Расстояния в Галактике и в Местной группе
[править | править код]Световое эхо
[править | править код]Примером оценки расстояния по световому эхо может служить сверхновая SN 1987A, вокруг которой образовалось кольцо, наклонённое к картинной плоскости. Всплески потока ультрафиолетового излучения от остатка сверхновой частично попадают на кольцо и заставляют его временно светиться ярче, что и называется световым эхо. При этом, поскольку разные части кольца находятся на разном расстоянии от Земли, рост их яркости происходит не одновременно. По задержке времени можно определить разность расстояний до разных частей кольца, а из его известной ориентации в пространстве — и линейные размеры. Поскольку угловые размеры кольца также известны, то можно определить расстояние, которое с помощью этого метода определяется как 47 килопарсек[15].
Лучевые скорости двойных звёзд
[править | править код]Если звёзды в двойной системе различимы по отдельности и при этом систему можно наблюдать как спектроскопическую двойную, то известны и угловые, и линейные размеры системы. Из соотношения между ними можно найти расстояние до системы[15].
Стандартные свечи
[править | править код]Стандартными свечами называют объекты, светимость которых известна заранее — можно обозначить абсолютную звёздную величину такого объекта как . Тогда, измерив видимую звёздную величину стандартной свечи , можно определить расстояние до неё. Если выражать в парсеках, то формула для связи этих величин примет следующий вид[22]:
Таким образом, разность видимой и абсолютной звёздной величины в этом случае служит мерой расстояния до объекта и её называют модулем расстояния[23].
Цефеиды
[править | править код]Цефеиды — класс пульсирующих переменных звёзд с хорошо изученной зависимостью между периодом и светимостью: чем ярче звезда, тем дольше её период пульсаций. Это позволяет определять светимость звезды, наблюдая период изменений её блеска. По спектральной классификации цефеиды являются жёлтыми гигантами и сверхгигантами, их средние абсолютные звёздные величины обычно находятся в диапазоне от 0m до −6m[24], так что их можно наблюдать на больших расстояниях, в том числе и в других галактиках. Существует две группы цефеид: I типа и II типа, с разной зависимостью между периодом и светимостью: цефеиды I типа в 4 раза ярче, чем цефеиды II типа при одинаковых периодах переменности. Кроме того, эти два типа звёзд относятся к разным типам звёздного населения[25].
Переменные типа RR Лиры
[править | править код]Переменные типа RR Лиры также относятся к пульсирующим переменным. Для них существует своя зависимость между периодом и светимостью, их средние абсолютные звёздные величины составляют 0,5―1m[24]. Эти звёзды относятся к старому населению II и из-за того, что они тусклее цефеид, обычно используются для измерения расстояний до шаровых звёздных скоплений, где довольно часто встречаются[26][27].
Сверхновые звёзды
[править | править код]Сверхновые типа Ia — катаклизмические переменные, которые при вспышке приобретают очень высокую светимость на некоторое время. При этом у более ярких сверхновых после достижения максимума блеска светимость понижается медленнее, чем у более тусклых. Сверхновые могут наблюдаться на очень больших расстояниях[15].
Ярчайшие звёзды галактик
[править | править код]Для галактик, в которых можно различить отдельные звёзды, можно измерять расстояние, исходя из грубого предположения, что для звёзд существует верхняя граница яркости. Тогда можно считать, что ярчайшие звёзды, наблюдаемые в галактике, имеют светимость, близкую к этой границе. Для больших выборок звёзд такой метод может давать приемлемую точность[15].
Подгонка главной последовательности
[править | править код]Кинематическая оценка расстояния
[править | править код]Метод Бааде — Весселинка
[править | править код]Метод расширяющейся фотосферы
[править | править код]Расстояния до ближайших скоплений галактик
[править | править код]Соотношение Талли — Фишера
[править | править код]Соотношение Фабер — Джексона
[править | править код]Эффект Сюняева — Зельдовича
[править | править код]Функция светимости планетарных туманностей
[править | править код]Флуктуации поверхностной яркости
[править | править код]Ярчайшие галактики скоплений
[править | править код]Расстояния на космологических масштабах
[править | править код]Закон Хаббла
[править | править код]Существенные неточности методов
[править | править код]История развития
[править | править код]В 1837 году Фридрих Бессель измерил параллакс звезды 61 Лебедя, тем самым определив расстояние до неё[28].
Примечания
[править | править код]- ↑ Расторгуев А. С. Шкала расстояний во вселенной. Астронет. Дата обращения: 18 февраля 2023.
- ↑ 1 2 The first rung on the cosmic distance ladder (англ.). ESO. Дата обращения: 19 февраля 2023.
- ↑ 1 2 Richmond M. What is the cosmological distance ladder? spiff.rit.edu. Дата обращения: 19 февраля 2023.
- ↑ 1 2 The Distance Ladder. www.e-education.psu.edu. Дата обращения: 19 февраля 2023.
- ↑ Binney, Merrifield, 1998, pp. 399—400, 407, 414.
- ↑ Binney, Merrifield, 1998, pp. 394—395, 414.
- ↑ Vallée J. P. Recent advances in the determination of some Galactic constants in the Milky Way // Astrophysics and Space Science. — 2017-04-01. — Т. 362. — С. 79. — ISSN 0004-640X. — doi:10.1007/s10509-017-3058-3.
- ↑ de Grijs, 2011, pp. 2—11.
- ↑ de Grijs, 2011, pp. 11—15.
- ↑ G. Pietrzyński, D. Graczyk, A. Gallenne, W. Gieren, I. B. Thompson, B. Pilecki, P. Karczmarek, M. Górski, K. Suchomska, M. Taormina, B. Zgirski, P. Wielgórski, Z. Kołaczkowski, P. Konorski, S. Villanova, N. Nardetto, P. Kervella, F. Bresolin, R. P. Kudritzki, J. Storm, R. Smolec, W. Narloch. A distance to the Large Magellanic Cloud that is precise to one per cent // Nature. — 2019-03-01. — Т. 567. — С. 200–203. — ISSN 0028-0836. — doi:10.1038/s41586-019-0999-4.
- ↑ Расстояний шкала. Энциклопедия физики и техники. Дата обращения: 19 февраля 2023.
- ↑ Richmond M. Distances within the Solar System. spiff.rit.edu. Дата обращения: 19 февраля 2023.
- ↑ 1 2 3 Жаров, 2006, с. 317—318.
- ↑ 1 2 Measuring Sizes and Distances. burro.case.edu. Дата обращения: 17 февраля 2023.
- ↑ 1 2 3 4 5 6 7 8 9 10 Wright E. L. The ABC's of Distances. astro.ucla.edu. Дата обращения: 17 февраля 2023.
- ↑ Кононович, Мороз, 2004, с. 51, 100.
- ↑ Karttunen et al., 2016, p. 28.
- ↑ 1 2 de Grijs, 2011, pp. 39—42.
- ↑ Холопов П. Н. Звездные скопления. 1.6 Открытие движущихся скоплений. Астронет. Дата обращения: 20 февраля 2023.
- ↑ Холопов П. Н. Звездные скопления. 3.3 Групповые параллаксы. Астронет. Дата обращения: 20 февраля 2023.
- ↑ 1 2 Karttunen et al., 2016, p. 362.
- ↑ Standard Candle. astronomy.swin.edu.au. Дата обращения: 7 марта 2023.
- ↑ Distance Modulus. astronomy.swin.edu.au. Дата обращения: 7 марта 2023.
- ↑ 1 2 Gary D. E. Pulsating and Variable Stars. web.njit.edu. Дата обращения: 10 марта 2023.
- ↑ Darling D. Cepheid variable. Internet Encyclopedia of Science. Дата обращения: 10 марта 2023.
- ↑ Darling D. RR Lyrae star. Internet Encyclopedia of Science. Дата обращения: 10 марта 2023.
- ↑ RR Lyrae. astronomy.swin.edu.au. Дата обращения: 10 марта 2023.
- ↑ Жаров, 2006, с. 36.
Литература
[править | править код]- Кононович Э. В., Мороз В. И. Общий курс астрономии. — 2-е, исправленное. — М.: УРСС, 2004. — 544 с. — ISBN 5-354-00866-2.
- Жаров В. Е. Сферическая астрономия. — Фрязино: Век 2, 2006. — 480 с. — (Монографии и учебники). — 500 экз. — ISBN 5-85099-168-9.
- Richard de Grijs. An introduction to distance measurement in astronomy. — Chichester, West Sussex: John Wiley and Sons, 2011. — 313 с. — ISBN 978-1-119-97818-3.
- Binney J., Merrifield M. Galactic Astronomy. — Princeton: Princeton University Press, 1998. — 816 p. — ISBN 978-0-691-23332-1.
- Karttunen H., Kroger P., Oja H., Poutanen M., Donner K. J. Fundamental Astronomy. — 6th Edition. — Berlin; Heidelberg; N. Y.: Springer, 2016. — 550 p. — ISBN 978-3-662-53045-0.














