經典控制理論

在控制理論中，經典控制理論（Classical control theory）是以拉普拉斯變換為分析工具，探討有控制系統之特性、以及反饋對系統特性的影響。

控制理論中常見的目標是要控制特定系統（稱為受控體），使其輸出可以依照控制信號（稱為參考信號，可能是定值或是變動量）。為了實現此目的，會設計控制器來監控輸出，並且比較輸出和參考信號。實際輸出和參考信號的差（稱為誤差信號）會反饋到控制器中，再由控制器產生受控體的輸入信號，使受控體的實際輸出接近參考信號。

經典控制理論主要處理線性時不變的單一輸入單一輸出系統，可以計算系統輸入信號及輸出信號的拉普拉斯變換，而系統的傳遞函數和輸入信號及輸出信號的拉普拉斯變換有關。

反饋

有些控制器不需要系統資訊，這類控制器稱為開迴路控制器，缺點是無法監控受控體的輸出，無法針對誤差進行修正。為了改善這些開迴路控制器的問題，經典控制理論引入了負反饋的概念，形成了閉迴路控制器。閉迴路控制器利用反饋來控制動力系統的狀態或是輸出。反饋是系統的訊號（例如電壓或是電流），對應受控體的狀態或輸出（例如電動機的速度或是轉矩）有關，反饋一般是透過傳感器量測到的訊號，再送回控制器為輸入訊號，因此形成一個迴路。

相較於開迴路控制器，閉迴路控制器有以下的優點：

• 抑制外來的干擾（例如以下例子中，開車遇到的坡度變化）。
• 即使數學模型存在不確定性，其模型無法完全模擬真實過程，或是模型參數不完全一致時，仍可以確保其性能。
• 可以將不穩定的系統變的穩定。
• 降低參數變化的敏感度。
• 提昇系統追隨參考命令的性能。

有些系統會同時使用開迴路控制及閉迴路控制，這類系統中的開迴路控制稱為前饋控制，目的是進一步提昇系統追隨參考命令的性能。

像PID控制器就是常見的閉迴路控制器。

經典控制及現代控制

控制系統可以在時域下建模，將系統的輸出表示為輸入、先前系統狀態及時間的函數。隨着時間變化，系統的狀態及輸出會隨之改變。不過系統的時域模型多半會是高階的微分方程，人工很不容易求解，有些方程甚至用電腦不容易快速的求解。

為了處理這樣的問題，經典控制理論使用拉普拉斯變換將時域的線性非時變常微分方程轉換為s域代數多項式。若系統轉換到s域中，在處理上會方便很多。

現代控制理論則用不同方式處理，會將常微分方程轉換為低階的時域微分方程組，對應的變數稱為狀態空間，後續則由線性代數的技巧來處理這些方程組。

拉普拉斯變換

主條目：拉普拉斯變換

經典控制理論會用拉普拉斯變換來為系統及信號建模，拉普拉斯變換是針對連續時間信號或系統的頻域分析工具，不論是否穩定都可以使用。一個定義在正t ≥ 0下的函數 f(t)，其拉普拉斯變換是函數F(s)，是以下式定義的單方向轉換

$F(s)=\int _{0}^{\infty }e^{-st}f(t)\,dt$

其中s是複數的頻率參數

$s=\sigma +i\omega$，其中σ和ω為實數。

閉迴路傳遞函數

系統的輸出y(t)會透過感測器量測設備F送回控制器，和參考值r(t)比較。控制器C會計算輸出和參考值之間的誤差e，並且調整受控系統P的輸入信號u。如圖所示，這類的控制器即為閉迴路控制器或回授控制器。

上述的系統稱為單一輸入單一輸出（SISO）系統，也有許多系統屬於多重輸入多重輸出（MIMO）系統，輸入及輸出信號不止一個。這類系統的輸入變數及輸出變數不會用純量表示，而是用向量表示。若是針對分佈式參數系統，其向量可能會是無限維數（多半會用函數表示）。

簡單的回授控制迴路

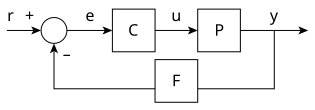
若假設控制器C、受控體P、感測器F都是線性，而且是時不變系統（其傳遞函數C(s)、P(s)、F(s)不會隨時間變化），上述的系統可以用拉普拉斯變換來分析，可得到下式：

$Y(s)=P(s)U(s)\,\!$

$U(s)=C(s)E(s)\,\!$

$E(s)=R(s)-F(s)Y(s).\,\!$

將Y(s)以R(s)來表示，可得

$Y(s)=\left({\frac {P(s)C(s)}{1+F(s)P(s)C(s)}}\right)R(s)=H(s)R(s).$

$H(s)={\frac {P(s)C(s)}{1+F(s)P(s)C(s)}}$就是系統的閉迴路傳遞函數，其分子是從r到y的前向（開迴路）增益，分母是1加上回授迴路的增益（稱為迴路增益）。若$|P(s)C(s)|\gg 1$，也就是對所有的s都有大的範數，且$|F(s)|\approx 1$，則Y(s)會近似R(s)，輸出會追隨參考輸入的變化。

PID控制器

更多資訊：PID控制器

PID控制器可能是最常使用的控制器，PID三個字母分別代表比例、積分及微分，是三種根據誤差訊號產生輸出控制信號的方式。令u(t)是送到受控系統的控制信號，y(t)是量測輸出、r(t)是理想的輸出信號，追隨誤差$e(t)=r(t)-y(t)$，PID控制器可以用下式表示

$u(t)=K_{P}e(t)+K_{I}\int e(t){\text{d}}t+K_{D}{\frac {\text{d}}{{\text{d}}t}}e(t).$

可以透過調整三個參數$K_{P}$, $K_{I}$ and $K_{D}$來得到理想的控制迴路動態，一般會反覆的調整，不一定需要有關受控系統的具體資訊。若只用比例控制，一般在適當的比例下可以確保其穩定性，積分項會消除步階擾動的影響（在過程控制中的重要規格），微分項是提供系統阻尼，或是調整響應特性。PID控制器是控制系統中最常用到的一種。不過不一定適用在許多複雜的應用中（例如多重輸入多重輸出系統）。

對PID控制器進行拉氏轉換可得到下式：

$u(s)=K_{P}e(s)+K_{I}{\frac {1}{s}}e(s)+K_{D}se(s)$

$u(s)=\left(K_{P}+K_{I}{\frac {1}{s}}+K_{D}s\right)e(s)$

可以得到其傳遞函數

$C(s)=\left(K_{P}+K_{I}{\frac {1}{s}}+K_{D}s\right).$

若將PID控制器表示為以下的形式

$C(s)=K\left(1+{\frac {1}{sT_{i}}}\right)(1+sT_{d})$

迴授迴路中的一階濾波器

$F(s)={\frac {1}{1+sT_{f}}}$

有濾波輸入的線性致動器

$P(s)={\frac {A}{1+sT_{p}}}$, A = const

將這些放在閉迴路傳遞函數H(s)的式子中，調適就很簡單了，只要令

$K={\frac {1}{A}},T_{i}=T_{f},T_{d}=T_{p}$

且令H(s) = 1。

在實際的PID控制器中，純微分器在物理上無法實現，也會引入一些不想要的特性，會放大高頻雜訊，也會增加系統的共振點，因此會改用相位領先的補償器，或是微分器再加上低通的滾降。

工具

經典控制理論中會使用許多工具來分析系統，並且設計控制器。工具包括有根軌跡圖、奈奎斯特穩定判據、波德圖、增益裕度及相位裕度等。

相關條目

• 狀態空間