截半正五胞體
外觀
| 截半正五胞體 | |
|---|---|
 | |
| 類型 | 均勻多胞體 |
| 識別 | |
| 名稱 | 截半正五胞體 |
| 參考索引 | 1 2 3 |
| 數學表示法 | |
| 考克斯特符號 | |
| 施萊夫利符號 | t1{3,3,3} |
| 性質 | |
| 胞 | 10 5 (3.3.3) 5 (3.3.3.3) |
| 面 | 30 {3} |
| 邊 | 30 |
| 頂點 | 10 |
| 組成與佈局 | |
| 頂點圖 |  三角柱 |
| 對稱性 | |
| 考克斯特群 | A4, [3,3,3], order 120 |
| 特性 | |
| convex, isogonal, isotoxal | |

5個面:


2(3.3.3)和3(3.3.3.3)
在四維幾何學中,截半正五胞體是一個由5個正四面體和5個正八面體胞組成的均勻多胞體。每條棱都連接到一個正四面體和兩個正八面體。每個頂點周圍環繞着兩個正四面體和三個正八面體。它總共有30個三角形面,30條棱和10個頂點。它的頂點圖是正三角柱。截半正五胞體是三個由兩種或更多的正多面體胞組成的四維半正多胞體之一。
構造
[編輯]截角正五胞體的細胞可以通過在正五胞體的棱的三分點處截斷其頂點。截斷的五個正四面體變成新的截角四面體,並在原來的頂點處產生了五個新的正四面體。
結合
[編輯]截角四面體的六邊形面彼此結合在一起,而它們的三角形面則連接到正四面體。
投影
[編輯]| Ak 考克斯特平面 |
A4 | A3 | A2 |
|---|---|---|---|
| Graph | 
|

|

|
| 二面體群 | [5] | [4] | [3] |
 施萊格爾投影 (對着一個正八面體胞) |
 展開圖 |

|
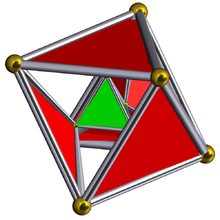
正四面體為中心的3維透視投影,最接近的正四面體呈紅色,周圍的4個正八面體呈綠色。遠端的胞清晰度降低(雖然可以從棱看出它們)。投影只是在三維空間中旋轉,而不是在四維空間中旋轉。 |
坐標
[編輯]一個棱長為2的截半正五胞體的頂點的笛卡兒坐標系坐標
|
|
|
更簡單的,截半正五胞體的頂點是五維空間笛卡兒坐標系的(0,0,0,1,1)或(0,0,1,1,1)的全排列。
參考文獻
[編輯]- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] (頁面存檔備份,存於互聯網檔案館)
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
外部連結
[編輯]- Rectified 5-cell (頁面存檔備份,存於互聯網檔案館) - data and images
- 1. Convex uniform polychora based on the pentachoron - Model 2, George Olshevsky.
- Klitzing, Richard. 4D uniform polytopes (polychora) x3o3o3o - rap. bendwavy.org.







