数学 中,Θ函数 是一种多复变 特殊函数 。其应用包括阿贝尔簇 模空间 、二次形式 、孤立子 理论;其格拉斯曼代数 推广亦出现于量子场论 ,尤其于超弦 与D-膜 理论。
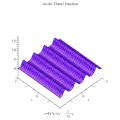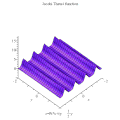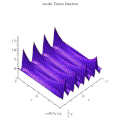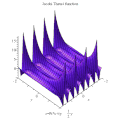
Jacobi theta 1 Jacobi theta 2 Jacobi theta 3 Jacobi theta 4 Θ函数最常见于椭圆函数 理论。相对于其“z ” 变量,Θ函数是拟周期函数 (quasiperiodic function),具有“拟周期性”。在一般下降理论 线丛
雅可比Θ函数取二变量
z
{\displaystyle z\,}
τ
{\displaystyle \tau \,}
z
{\displaystyle z\,}
复数 ,而
τ
{\displaystyle \tau \,}
上半复平面 上一点;此函数之定义为:
ϑ
(
z
;
τ
)
=
∑
n
=
−
∞
∞
e
(
π
i
n
2
τ
+
2
π
i
n
z
)
{\displaystyle \vartheta (z;\tau )=\sum _{n=-\infty }^{\infty }\ e^{(\pi in^{2}\tau +2\pi inz)}}
若固定
τ
{\displaystyle \tau \,}
1
{\displaystyle 1\,}
(
z
)
{\displaystyle (z)\,}
整函数 的傅里叶级数 :
ϑ
(
z
+
1
;
τ
)
=
ϑ
(
z
;
τ
)
{\displaystyle \vartheta (z+1;\tau )=\vartheta (z;\tau )}
在以
τ
{\displaystyle \tau \,}
ϑ
(
z
+
a
+
b
τ
;
τ
)
=
e
(
−
π
i
b
2
τ
−
2
π
i
b
z
)
ϑ
(
z
;
τ
)
{\displaystyle \vartheta (z+a+b\tau ;\tau )=\ e^{(-\pi ib^{2}\tau -2\pi ibz)}\vartheta (z;\tau )}
其中
a
{\displaystyle a\,}
b
{\displaystyle b\,}
可定义辅助函数:
ϑ
01
(
z
;
τ
)
=
ϑ
(
z
+
1
2
;
τ
)
{\displaystyle \vartheta _{01}(z;\tau )=\vartheta (z+{\frac {1}{2}};\tau )}
ϑ
10
(
z
;
τ
)
=
e
π
i
τ
4
+
π
i
z
ϑ
(
z
+
τ
2
;
τ
)
{\displaystyle \vartheta _{10}(z;\tau )=e^{{\frac {\pi {\mathrm {i} }\tau }{4}}+\pi {\mathrm {i} }z}\vartheta (z+{\frac {\tau }{2}};\tau )}
ϑ
11
(
z
;
τ
)
=
e
π
i
τ
4
+
π
i
(
z
+
1
2
)
ϑ
(
z
+
τ
+
1
2
;
τ
)
.
{\displaystyle \vartheta _{11}(z;\tau )=e^{{\frac {\pi {\mathrm {i} }\tau }{4}}+\pi {\mathrm {i} }(z+{\frac {1}{2}})}\vartheta (z+{\frac {\tau +1}{2}};\tau ).}
其中符号依黎曼 与芒福德 之习惯;雅可比 的原文用变量
q
=
e
π
i
τ
{\displaystyle q=e^{\pi {\mathrm {i} }\tau }\,}
τ
{\displaystyle \tau \,}
θ
3
{\displaystyle \theta _{3}\,}
ϑ
01
{\displaystyle \vartheta _{01}}
θ
0
{\displaystyle \theta _{0}\,}
ϑ
10
{\displaystyle \vartheta _{10}}
θ
2
{\displaystyle \theta _{2}\,}
ϑ
11
{\displaystyle \vartheta _{11}}
−
θ
1
{\displaystyle -\theta _{1}\,}
若设
z
=
0
{\displaystyle z=0\,}
τ
{\displaystyle \tau \,}
τ
{\displaystyle \tau \,}
模形式 ,或参数化某些曲线。由“雅可比 恒等式”可得:
ϑ
(
0
;
τ
)
4
=
ϑ
01
(
0
;
τ
)
4
+
ϑ
10
(
0
;
τ
)
4
{\displaystyle \vartheta (0;\tau )^{4}=\vartheta _{01}(0;\tau )^{4}+\vartheta _{10}(0;\tau )^{4}}
是为四次费马曲线 。
雅可比恒等式描述模群 在Θ函数之作用;模群之生成元为T: τ ↦ τ+1与S: τ ↦ -1/τ。我们已有 T 作用之式。设:
α
=
(
−
i
τ
)
1
2
e
π
i
z
2
τ
{\displaystyle \alpha =(-{\mathrm {i} }\tau )^{\frac {1}{2}}e^{{\pi {\mathrm {i} }z^{2}}{\tau }}\,}
则
ϑ
(
z
τ
;
−
1
τ
)
=
α
ϑ
(
z
;
τ
)
{\displaystyle \vartheta ({\frac {z}{\tau }};-{\frac {1}{\tau }})=\alpha \vartheta (z;\tau )}
ϑ
01
(
z
τ
;
−
1
τ
)
=
α
ϑ
10
(
z
;
τ
)
{\displaystyle \vartheta _{01}({\frac {z}{\tau }};-{\frac {1}{\tau }})=\alpha \vartheta _{10}(z;\tau )}
ϑ
10
(
z
τ
;
−
1
τ
)
=
α
ϑ
01
(
z
;
τ
)
{\displaystyle \vartheta _{10}({\frac {z}{\tau }};-{\frac {1}{\tau }})=\alpha \vartheta _{01}(z;\tau )}
ϑ
11
(
z
τ
;
−
1
τ
)
=
−
α
ϑ
11
(
z
;
τ
)
{\displaystyle \vartheta _{11}({\frac {z}{\tau }};-{\frac {1}{\tau }})=-\alpha \vartheta _{11}(z;\tau )}
我们可用变量
w
{\displaystyle w\,}
q
{\displaystyle q\,}
z
{\displaystyle z\,}
τ
{\displaystyle \tau \,}
w
=
e
π
i
z
{\displaystyle w=e^{\pi {\mathrm {i} }z}\,}
q
=
e
π
i
τ
{\displaystyle q=e^{\pi {\mathrm {i} }\tau }\,}
ϑ
(
w
;
q
)
=
∑
n
=
−
∞
∞
w
2
n
q
n
2
.
{\displaystyle \vartheta (w;q)=\sum _{n=-\infty }^{\infty }w^{2n}q^{n^{2}}.}
而辅助Θ函数可表示为:
ϑ
01
(
w
;
q
)
=
∑
n
=
−
∞
∞
(
−
1
)
n
w
2
n
q
n
2
,
{\displaystyle \vartheta _{01}(w;q)=\sum _{n=-\infty }^{\infty }(-1)^{n}w^{2n}q^{n^{2}},}
ϑ
10
(
w
;
q
)
=
q
1
4
∑
n
=
−
∞
∞
w
2
n
+
1
q
n
2
+
n
,
{\displaystyle \vartheta _{10}(w;q)=q^{\frac {1}{4}}\sum _{n=-\infty }^{\infty }w^{2n+1}q^{n^{2}+n},}
ϑ
11
(
w
;
q
)
=
i
q
1
4
∑
n
=
−
∞
∞
(
−
1
)
n
w
2
n
+
1
q
n
2
+
n
.
{\displaystyle \vartheta _{11}(w;q)={\mathrm {i} }q^{\frac {1}{4}}\sum _{n=-\infty }^{\infty }(-1)^{n}w^{2n+1}q^{n^{2}+n}.}
此表示式不需要指数函数 ,所以适用于指数函数无每一处定义域,如p进数 域。
雅可比三重积恒等式 (Jacobi's triple product identity)中指出:若有复数
w
{\displaystyle w\,}
q
{\displaystyle q\,}
|
q
|
<
1
{\displaystyle |q|<1\,}
w
≠
0
{\displaystyle w\neq 0\,}
∏
m
=
1
∞
(
1
−
q
2
m
)
(
1
+
w
2
q
2
m
−
1
)
(
1
+
w
−
2
q
2
m
−
1
)
=
∑
n
=
−
∞
∞
w
2
n
q
n
2
.
{\displaystyle \prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+w^{2}q^{2m-1}\right)\left(1+w^{-2}q^{2m-1}\right)=\sum _{n=-\infty }^{\infty }w^{2n}q^{n^{2}}.}
此式可以用基本方法证明,如戈弗雷·哈罗德·哈代 和爱德华·梅特兰·赖特 共同编著的《数论导引 》(英语:An Introduction to the Theory of Numbers
若用nome 变量
q
=
e
π
i
τ
{\displaystyle q=e^{\pi i\tau }\,}
w
=
e
π
i
z
{\displaystyle w=e^{\pi iz}\,}
ϑ
(
z
;
τ
)
=
∑
n
=
−
∞
∞
exp
(
π
i
τ
n
2
)
exp
(
π
i
z
2
n
)
=
∑
n
=
−
∞
∞
w
2
n
q
n
2
.
{\displaystyle \vartheta (z;\tau )=\sum _{n=-\infty }^{\infty }\exp(\pi i\tau n^{2})\exp(\pi iz2n)=\sum _{n=-\infty }^{\infty }w^{2n}q^{n^{2}}.}
由此得到Θ函数的积公式:
ϑ
(
z
;
τ
)
=
∏
m
=
1
∞
(
1
−
exp
(
2
m
π
i
τ
)
)
(
1
+
exp
(
(
2
m
−
1
)
π
i
τ
+
2
π
i
z
)
)
(
1
+
exp
(
(
2
m
−
1
)
π
i
τ
−
2
π
i
z
)
)
{\displaystyle \vartheta (z;\tau )=\prod _{m=1}^{\infty }\left(1-\exp(2m\pi i\tau )\right)\left(1+\exp((2m-1)\pi i\tau +2\pi iz)\right)\left(1+\exp((2m-1)\pi i\tau -2\pi iz)\right)}
三重积等式左边可以扩展成:
∏
m
=
1
∞
(
1
−
q
2
m
)
(
1
+
(
w
2
+
w
−
2
)
q
2
m
−
1
+
q
4
m
−
2
)
,
{\displaystyle \prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+(w^{2}+w^{-2})q^{2m-1}+q^{4m-2}\right),}
即
ϑ
(
z
|
q
)
=
∏
m
=
1
∞
(
1
−
q
2
m
)
(
1
+
2
cos
(
2
π
z
)
q
2
m
−
1
+
q
4
m
−
2
)
{\displaystyle \vartheta (z|q)=\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+2\cos(2\pi z)q^{2m-1}+q^{4m-2}\right)}
这个式子在z 取实值时尤为重要。
各辅助Θ函数亦有类似之积公式:
ϑ
01
(
z
|
q
)
=
∏
m
=
1
∞
(
1
−
q
2
m
)
(
1
−
2
cos
(
2
π
z
)
q
2
m
−
1
+
q
4
m
−
2
)
.
{\displaystyle \vartheta _{01}(z|q)=\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1-2\cos(2\pi z)q^{2m-1}+q^{4m-2}\right).}
ϑ
10
(
z
|
q
)
=
2
q
1
/
4
cos
(
π
z
)
∏
m
=
1
∞
(
1
−
q
2
m
)
(
1
+
2
cos
(
2
π
z
)
q
2
m
+
q
4
m
)
.
{\displaystyle \vartheta _{10}(z|q)=2q^{1/4}\cos(\pi z)\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+2\cos(2\pi z)q^{2m}+q^{4m}\right).}
ϑ
11
(
z
|
q
)
=
−
2
q
1
/
4
sin
(
π
z
)
∏
m
=
1
∞
(
1
−
q
2
m
)
(
1
−
2
cos
(
2
π
z
)
q
2
m
+
q
4
m
)
.
{\displaystyle \vartheta _{11}(z|q)=-2q^{1/4}\sin(\pi z)\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1-2\cos(2\pi z)q^{2m}+q^{4m}\right).}
雅可比Θ函数可用积分表示,如下:
ϑ
(
z
;
τ
)
=
−
i
∫
i
−
∞
i
+
∞
e
i
π
τ
u
2
cos
(
2
u
z
+
π
u
)
sin
(
π
u
)
d
u
{\displaystyle \vartheta (z;\tau )=-i\int _{i-\infty }^{i+\infty }{e^{i\pi \tau u^{2}}\cos(2uz+\pi u) \over \sin(\pi u)}du}
ϑ
01
(
z
;
τ
)
=
−
i
∫
i
−
∞
i
+
∞
e
i
π
τ
u
2
cos
(
2
u
z
)
sin
(
π
u
)
d
u
.
{\displaystyle \vartheta _{01}(z;\tau )=-i\int _{i-\infty }^{i+\infty }{e^{i\pi \tau u^{2}}\cos(2uz) \over \sin(\pi u)}du.}
ϑ
10
(
z
;
τ
)
=
−
i
e
i
z
+
i
π
τ
/
4
∫
i
−
∞
i
+
∞
e
i
π
τ
u
2
cos
(
2
u
z
+
π
u
+
π
τ
u
)
sin
(
π
u
)
d
u
{\displaystyle \vartheta _{10}(z;\tau )=-ie^{iz+i\pi \tau /4}\int _{i-\infty }^{i+\infty }{e^{i\pi \tau u^{2}}\cos(2uz+\pi u+\pi \tau u) \over \sin(\pi u)}du}
ϑ
11
(
z
;
τ
)
=
e
i
z
+
i
π
τ
/
4
∫
i
−
∞
i
+
∞
e
i
π
τ
u
2
cos
(
2
u
z
+
π
τ
u
)
sin
(
π
u
)
d
u
{\displaystyle \vartheta _{11}(z;\tau )=e^{iz+i\pi \tau /4}\int _{i-\infty }^{i+\infty }{e^{i\pi \tau u^{2}}\cos(2uz+\pi \tau u) \over \sin(\pi u)}du}
黎曼 常用关系式
ϑ
(
0
;
−
1
τ
)
=
(
−
i
τ
)
1
2
ϑ
(
0
;
τ
)
{\displaystyle \vartheta (0;-{\frac {1}{\tau }})=(-i\tau )^{\frac {1}{2}}\vartheta (0;\tau )}
以证黎曼ζ函数 之函数方程 。他写下等式:
Γ
(
s
2
)
π
−
s
2
ζ
(
s
)
=
1
2
∫
0
∞
[
ϑ
(
0
;
i
t
)
−
1
]
t
s
2
d
t
t
{\displaystyle \Gamma \left({\frac {s}{2}}\right)\pi ^{-{\frac {s}{2}}}\zeta (s)={\frac {1}{2}}\int _{0}^{\infty }\left[\vartheta (0;it)-1\right]t^{\frac {s}{2}}{\frac {dt}{t}}}
而此积分于替换
s
→
1
−
s
{\displaystyle s\to 1-s}
z
{\displaystyle z\,}
赫尔维茨ζ函数 一文有描述。
雅可比用Θ函数来构造椭圆函数,并使其有易于计算之形式,因为Θ函数中快速收敛的级数往往比积分容易计算。他表示他的椭圆函数成两枚上述Θ函数之商,这可参见雅可比椭圆函数 的定义。魏尔施特拉斯椭圆函数 亦可由雅可比Θ构造:
℘
(
z
;
τ
)
=
−
(
log
ϑ
11
(
z
;
τ
)
)
″
+
c
{\displaystyle \wp (z;\tau )=-(\log \vartheta _{11}(z;\tau ))''+c}
其中二次微分相对于z ,而常数c 使
℘
(
z
)
{\displaystyle \wp (z)}
罗朗级数 (于 z = 0)常项为零,因为雅可比椭圆函数单位胞腔内两极点互为相反数,和为零,而魏尔施特拉斯椭圆函数的所有极点留数均为零,所以这是必要的。
设η为戴德金η函数 。则
ϑ
(
0
;
τ
)
=
η
2
(
τ
+
1
2
)
η
(
2
τ
+
1
)
{\displaystyle \vartheta (0;\tau )={\frac {\eta ^{2}\left(\tau +{\frac {1}{2}}\right)}{\eta (2\tau +1)}}}
雅可比Θ函数为一维热方程 、于时间为零时符合周期边界条件之唯一解。 设z = x 取实值,τ = it 而t 取正值。则有
ϑ
(
x
,
i
t
)
=
1
+
2
∑
n
=
1
∞
exp
(
−
π
n
2
t
)
cos
(
2
π
n
x
)
{\displaystyle \vartheta (x,it)=1+2\sum _{n=1}^{\infty }\exp(-\pi n^{2}t)\cos(2\pi nx)}
此解此下方程:
∂
∂
t
ϑ
(
x
,
i
t
)
=
1
4
π
∂
2
∂
x
2
ϑ
(
x
,
i
t
)
{\displaystyle {\frac {\partial }{\partial t}}\vartheta (x,it)={\frac {1}{4\pi }}{\frac {\partial ^{2}}{\partial x^{2}}}\vartheta (x,it)}
于t = 0时,Θ函数成为“狄拉克梳状函数 ”(Dirac comb)
lim
t
→
0
ϑ
(
x
,
i
t
)
=
∑
n
=
−
∞
∞
δ
(
x
−
n
)
{\displaystyle \lim _{t\rightarrow 0}\vartheta (x,it)=\sum _{n=-\infty }^{\infty }\delta (x-n)}
其中δ为狄拉克δ函数 ,故可知此解是唯一的。
因此,一般解可得自t = 0时的(周期)边界条件与Θ函数的卷积。
雅可比Θ函在海森堡群 之一离散子群作用下不变。见海森堡群之Θ表示 一文。
若F 为一n 元二次型 ,则有一关连的Θ函数
θ
F
(
z
)
=
∑
m
∈
Z
n
exp
(
2
π
i
z
F
(
m
)
)
{\displaystyle \theta _{F}(z)=\sum _{m\in Z^{n}}\exp(2\pi izF(m))}
其中Z n 为整数格 。此Θ函数是模群(或某适当子群)上的权n /2 模形式 。在其富理埃级数
θ
F
(
z
)
=
∑
k
=
0
∞
R
F
(
k
)
exp
(
2
π
i
k
z
)
{\displaystyle \theta _{F}(z)=\sum _{k=0}^{\infty }R_{F}(k)\exp(2\pi ikz)}
中,R F (k ) 称为此模形式之“表示数 ”(representation numbers)。
设
H
n
=
{
F
∈
M
(
n
,
C
)
s
.
t
.
F
=
F
T
and
Im
F
>
0
}
{\displaystyle \mathbb {H} _{n}=\{F\in M(n,\mathbb {C} )\;\mathrm {s.t.} \,F=F^{T}\;{\textrm {and}}\;{\mbox{Im}}F>0\}}
为一集对称方矩阵,其虚部为正定 ,一般称H n 西格尔上半平面 ”(Siegel upper half-plane),它是上半复平面 的高维推广。模群之n 维推广为辛群 Sp(2n,Z ): 当n = 1 时, Sp(2,Z ) = SL(2,Z )。同余子群 (congruence subgroup)的n 维推广为态射核
Ker
{
Sp
(
2
n
,
Z
)
→
Sp
(
2
n
,
Z
/
k
Z
)
}
{\displaystyle {\textrm {Ker}}\{{\textrm {Sp}}(2n,\mathbb {Z} )\rightarrow {\textrm {Sp}}(2n,\mathbb {Z} /k\mathbb {Z} )\}}
若设
τ
∈
H
n
{\displaystyle \tau \in \mathbb {H} _{n}}
黎曼Θ函数 :
θ
(
z
,
τ
)
=
∑
m
∈
Z
n
exp
(
2
π
i
(
1
2
m
T
τ
m
+
m
T
z
)
)
{\displaystyle \theta (z,\tau )=\sum _{m\in Z^{n}}\exp \left(2\pi i\left({\frac {1}{2}}m^{T}\tau m+m^{T}z\right)\right)}
θ
(
z
,
τ
)
=
∑
m
∈
Z
n
exp
(
2
π
i
(
1
2
m
T
τ
m
+
m
T
z
)
)
{\displaystyle \theta (z,\tau )=\sum _{m\in Z^{n}}\exp \left(2\pi i\left({\frac {1}{2}}m^{T}\tau m+m^{T}z\right)\right)}
其中
z
∈
C
n
{\displaystyle z\in \mathbb {C} ^{n}}
n 维复向量,上标T 为转置 。然则雅可比Θ函数为其特例(设n = 1、
τ
∈
H
{\displaystyle \tau \in \mathbb {H} }
H
{\displaystyle \mathbb {H} }
在
C
n
×
H
n
.
{\displaystyle \mathbb {C} ^{n}\times \mathbb {H} _{n}.}
函数方程为:
θ
(
z
+
a
+
τ
b
,
τ
)
=
exp
2
π
i
(
−
b
T
z
−
1
2
b
T
τ
b
)
θ
(
z
,
τ
)
{\displaystyle \theta (z+a+\tau b,\tau )=\exp 2\pi i\left(-b^{T}z-{\frac {1}{2}}b^{T}\tau b\right)\theta (z,\tau )}
此方程成立于
a
,
b
∈
Z
n
{\displaystyle a,b\in \mathbb {Z} ^{n}}
z
∈
C
n
{\displaystyle z\in \mathbb {C} ^{n}}
τ
∈
H
n
{\displaystyle \tau \in \mathbb {H} _{n}}
Milton Abramowitz and Irene A. Stegun, Handbook of Mathematical Functions , (1964) Dover Publications, New York. ISBN 0-486-61272-4 . (See section 16.27ff.)
Naum Illyich Akhiezer, Elements of the Theory of Elliptic Functions , (1970) Moscow, translated into English as AMS Translations of Mathematical Monographs Volume 79 (1990) AMS, Rhode Island ISBN 0-8218-4532-2
Hershel M. Farkas and Irwin Kra, Riemann Surfaces (1980), Springer-Verlag, New York. ISBN 0-387-90465-4 (See Chapter 6 for treatment of the Riemann theta)
G. H. Hardy and E. M. Wright,An Introduction to the Theory of Numbers , fourth edition (1959) , Oxford University Press
David Mumford,Tata Lectures on Theta I (1983), Birkhauser, Boston ISBN 3-7643-3109-7
James Pierpont Functions of a Complex Variable , Dover
Harry E. Rauch and Hershel M. Farkas, Theta Functions with Applications to Riemann Surfaces , (1974) Williams & Wilkins Co. Baltimore ISBN 0-683-07196-3 . 本条目含有来自PlanetMath 《Integral representations of Jacobi theta functions 》的内容,版权遵守知识共享协议:署名-相同方式共享 协议 。



























































![{\displaystyle \Gamma \left({\frac {s}{2}}\right)\pi ^{-{\frac {s}{2}}}\zeta (s)={\frac {1}{2}}\int _{0}^{\infty }\left[\vartheta (0;it)-1\right]t^{\frac {s}{2}}{\frac {dt}{t}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/11e177b4d51b05c325820f3731b7852cec448541)


















