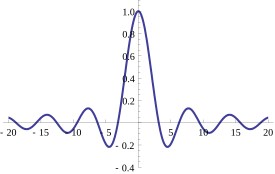
The characteristic function of a uniform U (–1,1) random variable. This function is real-valued because it corresponds to a random variable that is symmetric around the origin; however characteristic functions may generally be complex-valued. 在概率论 中,任何随机变量 的特征函数 (缩写:ch.f,复数形式:ch.f's)完全定义了它的概率分布 。在实 直线上,它由以下公式给出,其中
X
{\displaystyle X}
φ
X
(
t
)
=
E
(
e
i
t
X
)
{\displaystyle \varphi _{X}(t)=\operatorname {E} \left(e^{itX}\right)}
其中
t
{\displaystyle t}
实数 ,
i
{\displaystyle i}
虚数单位 ,
E
{\displaystyle E}
期望 。
用矩母函数
M
X
(
t
)
{\displaystyle M_{X}(t)}
i
X
{\displaystyle iX}
X
{\displaystyle X}
φ
X
(
t
)
=
M
i
X
(
t
)
=
M
X
(
i
t
)
{\displaystyle \varphi _{X}(t)=M_{iX}(t)=M_{X}(it)}
与矩母函数不同,特征函数总是存在。
如果
F
X
{\displaystyle F_{X}}
累积分布函数 ,那么特征函数由黎曼-斯蒂尔杰斯积分 给出:
E
(
e
i
t
X
)
=
∫
−
∞
∞
e
i
t
x
d
F
X
(
x
)
{\displaystyle \operatorname {E} \left(e^{itX}\right)=\int _{-\infty }^{\infty }e^{itx}\,dF_{X}(x)}
在概率密度函数
f
X
{\displaystyle f_{X}}
E
(
e
i
t
X
)
=
∫
−
∞
∞
e
i
t
x
f
X
(
x
)
d
x
{\displaystyle \operatorname {E} \left(e^{itX}\right)=\int _{-\infty }^{\infty }e^{itx}f_{X}(x)\,dx}
如果
X
{\displaystyle X}
向量 值随机变量,我们便取自变量
t
{\displaystyle t}
t
X
{\displaystyle tX}
数量积 。
R
{\displaystyle R}
R
n
{\displaystyle R^{n}}
测度 的空间上对一个有界函数 进行积分,且对于每一个特征函数都正好有一个概率分布。
一个对称概率密度函数的特征函数(也就是满足
f
X
(
x
)
=
f
X
(
−
x
)
{\displaystyle f_{X}(x)=f_{X}(-x)}
x
>
0
{\displaystyle x>0}
x
<
0
{\displaystyle x<0}
勒维连续定理 说明,假设
(
X
n
)
n
=
1
∞
{\displaystyle (X_{n})_{n=1}^{\infty }}
X
n
{\displaystyle X_{n}}
φ
n
{\displaystyle \varphi _{n}}
X
{\displaystyle X}
X
n
→
D
X
{\displaystyle X_{n}{\xrightarrow {\mathcal {D}}}X}
n
→
∞
{\displaystyle n\to \infty }
如果
φ
n
→
pointwise
φ
{\displaystyle \varphi _{n}\quad {\xrightarrow {\textrm {pointwise}}}\quad \varphi }
n
→
∞
{\displaystyle n\to \infty }
且
φ
(
t
)
{\displaystyle \varphi (t)}
t
=
0
{\displaystyle \ t=0}
φ
{\displaystyle \varphi }
X
{\displaystyle X}
勒维连续定理可以用来证明弱大数定律 。
在累积概率分布函数与特征函数之间存在双射 。也就是说,两个不同的概率分布不能有相同的特征函数。
给定一个特征函数φ,可以用以下公式求得对应的累积概率分布函数
F
{\displaystyle F}
F
X
(
y
)
−
F
X
(
x
)
=
lim
τ
→
+
∞
1
2
π
∫
−
τ
+
τ
e
−
i
t
x
−
e
−
i
t
y
i
t
φ
X
(
t
)
d
t
{\displaystyle F_{X}(y)-F_{X}(x)=\lim _{\tau \to +\infty }{\frac {1}{2\pi }}\int _{-\tau }^{+\tau }{\frac {e^{-itx}-e^{-ity}}{it}}\,\varphi _{X}(t)\,dt}
一般地,这是一个广义积分 ;被积分的函数可能只是条件可积而不是勒贝格可积 的,也就是说,它的绝对值 的积分可能是无穷大。[ 1]
任意一个函数
φ
{\displaystyle \varphi }
μ
{\displaystyle \mu }
φ
{\displaystyle \varphi \,}
φ
(
0
)
=
1
{\displaystyle \varphi (0)=1\,}
φ
{\displaystyle \varphi \,}
正定函数 (注意这是一个复杂的条件,与
φ
>
0
{\displaystyle \varphi >0}
特征函数对于处理独立 随机变量的函数特别有用。例如,如果
X
1
{\displaystyle X_{1}}
X
2
{\displaystyle X_{2}}
X
n
{\displaystyle X_{n}}
S
n
=
∑
i
=
1
n
a
i
X
i
,
{\displaystyle S_{n}=\sum _{i=1}^{n}a_{i}X_{i},\,\!}
其中
a
i
{\displaystyle a_{i}}
S
n
{\displaystyle S_{n}}
φ
S
n
(
t
)
=
φ
X
1
(
a
1
t
)
φ
X
2
(
a
2
t
)
⋯
φ
X
n
(
a
n
t
)
.
{\displaystyle \varphi _{S_{n}}(t)=\varphi _{X_{1}}(a_{1}t)\varphi _{X_{2}}(a_{2}t)\cdots \varphi _{X_{n}}(a_{n}t).\,\!}
特别地,
φ
X
+
Y
(
t
)
=
φ
X
(
t
)
φ
Y
(
t
)
{\displaystyle \varphi _{X+Y}(t)=\varphi _{X}(t)\varphi _{Y}(t)}
φ
X
+
Y
(
t
)
=
E
(
e
i
t
(
X
+
Y
)
)
=
E
(
e
i
t
X
e
i
t
Y
)
=
E
(
e
i
t
X
)
E
(
e
i
t
Y
)
=
φ
X
(
t
)
φ
Y
(
t
)
{\displaystyle \varphi _{X+Y}(t)=E\left(e^{it(X+Y)}\right)=E\left(e^{itX}e^{itY}\right)=E\left(e^{itX}\right)E\left(e^{itY}\right)=\varphi _{X}(t)\varphi _{Y}(t)}
注意我们需要
X
{\displaystyle X}
Y
{\displaystyle Y}
另外一个特殊情况,是
a
i
=
1
n
{\displaystyle a_{i}={\frac {1}{n}}}
S
n
{\displaystyle S_{n}}
X
¯
{\displaystyle {\overline {X}}}
φ
X
¯
(
t
)
=
(
φ
X
(
t
n
)
)
n
{\displaystyle \varphi _{\overline {X}}(t)=\left(\varphi _{X}\left({\frac {t}{n}}\right)\right)^{n}}
分布
特征函数
φ
(
t
)
{\displaystyle \varphi (t)}
退化分布
δ
a
{\displaystyle \delta _{a}}
e
i
t
a
{\displaystyle e^{ita}}
伯努利分布
B
e
r
n
(
p
)
{\displaystyle \mathrm {Bern} (p)}
1
−
p
+
p
e
i
t
{\displaystyle 1-p+pe^{it}}
二项分布
B
(
n
,
p
)
{\displaystyle B(n,p)}
(
1
−
p
+
p
e
i
t
)
n
{\displaystyle (1-p+pe^{it})^{n}}
负二项分布
N
B
(
r
,
p
)
{\displaystyle NB(r,p)}
(
1
−
p
1
−
p
e
i
t
)
r
{\displaystyle {\biggl (}{\frac {1-p}{1-pe^{i\,t}}}{\biggr )}^{\!r}}
泊松分布
P
o
i
s
(
λ
)
{\displaystyle \mathrm {Pois} (\lambda )}
e
λ
(
e
i
t
−
1
)
{\displaystyle e^{\lambda (e^{it}-1)}}
连续均匀分布
U
(
a
,
b
)
{\displaystyle U(a,b)}
e
i
t
b
−
e
i
t
a
i
t
(
b
−
a
)
{\displaystyle {\frac {e^{itb}-e^{ita}}{it(b-a)}}}
拉普拉斯分布
L
(
μ
,
b
)
{\displaystyle L(\mu ,b)}
e
i
t
μ
1
+
b
2
t
2
{\displaystyle {\frac {e^{it\mu }}{1+b^{2}t^{2}}}}
常态分布
N
(
μ
,
σ
2
)
{\displaystyle N(\mu ,\sigma ^{2})}
e
i
t
μ
−
1
2
σ
2
t
2
{\displaystyle e^{it\mu -{\frac {1}{2}}\sigma ^{2}t^{2}}}
卡方分布
χ
k
2
{\displaystyle \chi _{k}^{2}}
k
(
1
−
2
i
t
)
−
k
2
{\displaystyle (1-2it)^{-{\frac {k}{2}}}}
柯西分布
C
(
μ
,
θ
)
{\displaystyle C(\mu ,\theta )}
e
i
t
μ
−
θ
|
t
|
{\displaystyle e^{it\mu -\theta |t|}}
伽玛分布
Γ
(
k
,
θ
)
{\displaystyle \Gamma (k,\theta )}
(
1
−
i
t
θ
)
−
k
{\displaystyle (1-it\theta )^{-k}}
指数分布
E
x
p
(
λ
)
{\displaystyle \mathrm {Exp} (\lambda )}
(
1
−
i
t
λ
−
1
)
−
1
{\displaystyle (1-it\lambda ^{-1})^{-1}}
多元常态分布
N
(
μ
,
Σ
)
{\displaystyle N(\mu ,\Sigma )}
e
i
t
T
μ
−
1
2
t
T
Σ
t
{\displaystyle e^{it^{T}\mu -{\frac {1}{2}}t^{T}\Sigma t}}
多元柯西分布
M
u
l
t
i
C
a
u
c
h
y
(
μ
,
Σ
)
{\displaystyle \mathrm {MultiCauchy} (\mu ,\Sigma )}
[ 2]
e
i
t
T
μ
−
t
T
Σ
t
{\displaystyle e^{it^{T}\mu -{\sqrt {t^{T}\Sigma t}}}}
Oberhettinger (1973) 提供的特征函数表.
由于连续定理 ,特征函数被用于中心极限定理 的最常见的证明中。
特征函数还可以用来求出某个随机变量的矩 。只要第n 个矩存在,特征函数就可以微分n 次,得到:
E
(
X
n
)
=
i
−
n
φ
X
(
n
)
(
0
)
=
i
−
n
[
d
n
d
t
n
φ
X
(
t
)
]
t
=
0
.
{\displaystyle \operatorname {E} \left(X^{n}\right)=i^{-n}\,\varphi _{X}^{(n)}(0)=i^{-n}\,\left[{\frac {d^{n}}{dt^{n}}}\varphi _{X}(t)\right]_{t=0}.\,\!}
例如,假设
X
{\displaystyle X}
柯西分布 。那么
φ
X
(
t
)
=
e
−
|
t
|
{\displaystyle \varphi _{X}(t)=e^{-|t|}}
t
=
0
{\displaystyle t=0}
可微 ,说明柯西分布没有期望 。另外,注意到
n
{\displaystyle n}
独立 的观测的样本平均值
X
¯
{\displaystyle {\overline {X}}}
φ
X
¯
(
t
)
=
(
e
−
|
t
|
n
)
n
=
e
−
|
t
|
{\displaystyle \varphi _{\overline {X}}(t)=(e^{-{\frac {\left\vert t\right\vert }{n}}})^{n}=e^{-|t|}}
特征函数的对数是一个累积量母函数 ,它对于求出累积量是十分有用的;注意有时定义累积量母函数为矩母函数 的对数,而把特征函数的对数称为第二 累积量母函数。
具有尺度参数
θ
{\displaystyle \theta }
k 的伽玛分布 的特征函数为:
(
1
−
θ
i
t
)
−
k
{\displaystyle (1-\theta \,i\,t)^{-k}}
现在假设我们有:
X
∼
Γ
(
k
1
,
θ
)
{\displaystyle \ X\sim \Gamma (k_{1},\theta )}
Y
∼
Γ
(
k
2
,
θ
)
{\displaystyle \ Y\sim \Gamma (k_{2},\theta )}
其中
X
{\displaystyle X}
Y
{\displaystyle Y}
X
+
Y
{\displaystyle X+Y}
X
{\displaystyle X}
Y
{\displaystyle Y}
φ
X
(
t
)
=
(
1
−
θ
i
t
)
−
k
1
,
φ
Y
(
t
)
=
(
1
−
θ
i
t
)
−
k
2
{\displaystyle \varphi _{X}(t)=(1-\theta \,i\,t)^{-k_{1}},\,\qquad \varphi _{Y}(t)=(1-\theta \,i\,t)^{-k_{2}}}
根据独立性和特征函数的基本性质,可得:
φ
X
+
Y
(
t
)
=
φ
X
(
t
)
φ
Y
(
t
)
=
(
1
−
θ
i
t
)
−
k
1
(
1
−
θ
i
t
)
−
k
2
=
(
1
−
θ
i
t
)
−
(
k
1
+
k
2
)
{\displaystyle \varphi _{X+Y}(t)=\varphi _{X}(t)\varphi _{Y}(t)=(1-\theta \,i\,t)^{-k_{1}}(1-\theta \,i\,t)^{-k_{2}}=\left(1-\theta \,i\,t\right)^{-(k_{1}+k_{2})}}
这就是尺度参数为
θ
{\displaystyle \theta }
k
1
+
k
2
{\displaystyle k_{1}+k_{2}}
X
+
Y
∼
Γ
(
k
1
+
k
2
,
θ
)
{\displaystyle X+Y\sim \Gamma (k_{1}+k_{2},\theta )}
这个结果可以推广到
n
{\displaystyle n}
∀
i
∈
{
1
,
…
,
n
}
:
X
i
∼
Γ
(
k
i
,
θ
)
⇒
∑
i
=
1
n
X
i
∼
Γ
(
∑
i
=
1
n
k
i
,
θ
)
{\displaystyle \forall i\in \{1,\ldots ,n\}:X_{i}\sim \Gamma (k_{i},\theta )\qquad \Rightarrow \qquad \sum _{i=1}^{n}X_{i}\sim \Gamma \left(\sum _{i=1}^{n}k_{i},\theta \right)}
如果
X
{\displaystyle X}
φ
X
(
t
)
=
E
(
e
i
t
⋅
X
)
{\displaystyle \varphi _{X}(t)=\operatorname {E} \left(e^{it\cdot X}\right)}
这里的点表示向量的点积 ,而向量
t
{\displaystyle t}
X
{\displaystyle X}
对偶空间 内。用更加常见的矩阵表示法,就是:
φ
X
(
t
)
=
E
(
e
i
t
T
X
)
{\displaystyle \varphi _{X}(t)=\operatorname {E} \left(e^{it^{T}X}\right)}
如果
X
∼
N
(
0
,
Σ
)
{\displaystyle X\sim N(0,\Sigma )\,}
多元高斯 随机变量,那么:
φ
X
(
t
)
=
E
(
e
i
t
T
X
)
=
∫
x
∈
R
n
1
(
2
π
)
n
/
2
|
Σ
|
1
/
2
e
−
1
2
x
T
Σ
−
1
x
⋅
e
i
t
T
x
d
x
=
e
−
1
2
t
T
Σ
t
,
t
∈
R
n
,
{\displaystyle \varphi _{X}(t)=\operatorname {E} \left(e^{it^{T}X}\right)=\int _{x\in \mathbf {R} ^{n}}{\frac {1}{\left(2\pi \right)^{n/2}\left|\Sigma \right|^{1/2}}}\,e^{-{\frac {1}{2}}x^{T}\Sigma ^{-1}x}\cdot e^{it^{T}x}\,dx=e^{-{\frac {1}{2}}t^{T}\Sigma t},\quad t\in \mathbf {R} ^{n},}
其中
|
Σ
|
{\displaystyle |\Sigma |}
正定矩阵 Σ的行列式。
如果
X
{\displaystyle X}
φ
X
(
T
)
=
E
(
e
i
T
r
(
X
T
)
)
{\displaystyle \varphi _{X}(T)=\operatorname {E} \left(e^{i\,\mathrm {Tr} (XT)}\right)}
在这里,
T
r
(
⋅
)
{\displaystyle \mathrm {Tr} (\cdot )}
迹 函数,
X
T
{\displaystyle \ XT}
T
{\displaystyle T}
X
{\displaystyle X}
XT 一定有迹,因此矩阵X 必须与矩阵T 的转置 的大小相同;因此,如果X 是m × n 矩阵,那么T 必须是n × m 矩阵。
注意乘法的顺序不重要(
X
T
≠
T
X
{\displaystyle XT\neq TX}
t
r
(
X
T
)
=
t
r
(
T
X
)
{\displaystyle \ tr(XT)=tr(TX)}
矩阵值随机变量的例子包括威沙特分布 和矩阵常态分布 。
相关概念有矩母函数 和概率母函数 。特征函数对于所有概率分布都存在,但矩母函数不是这样。
特征函数与傅里叶变换 有密切的关系:一个概率密度函数
p
(
x
)
{\displaystyle p(x)}
p
(
x
)
{\displaystyle p(x)}
连续傅里叶变换 的共轭复数 (按照通常的惯例)。
φ
X
(
t
)
=
⟨
e
i
t
X
⟩
=
∫
−
∞
∞
e
i
t
x
p
(
x
)
d
x
=
(
∫
−
∞
∞
e
−
i
t
x
p
(
x
)
d
x
)
¯
=
P
(
t
)
¯
,
{\displaystyle \varphi _{X}(t)=\langle e^{itX}\rangle =\int _{-\infty }^{\infty }e^{itx}p(x)\,dx={\overline {\left(\int _{-\infty }^{\infty }e^{-itx}p(x)\,dx\right)}}={\overline {P(t)}},}
其中
P
(
t
)
{\displaystyle P(t)}
p
(
x
)
{\displaystyle p(x)}
连续傅里叶变换 。类似地,从
φ
X
(
t
)
{\displaystyle \varphi _{X}(t)}
p
(
x
)
{\displaystyle p(x)}
p
(
x
)
=
1
2
π
∫
−
∞
∞
e
i
t
x
P
(
t
)
d
t
=
1
2
π
∫
−
∞
∞
e
i
t
x
φ
X
(
t
)
¯
d
t
{\displaystyle p(x)={\frac {1}{2\pi }}\int _{-\infty }^{\infty }e^{itx}P(t)\,dt={\frac {1}{2\pi }}\int _{-\infty }^{\infty }e^{itx}{\overline {\varphi _{X}(t)}}\,dt}
确实,即使当随机变量没有密度时,特征函数仍然可以视为对应于该随机变量的测度的傅里叶变换。
^ P. Levy, Calcul des probabilités, Gauthier-Villars, Paris, 1925. p. 166
^ Kotz et al. p. 37 using 1 as the number of degree of freedom to recover the Cauchy distribution
Lukacs E. (1970) Characteristic Functions. Griffin, London. pp. 350
Bisgaard, T. M., Sasvári, Z. (2000) Characteristic Functions and Moment Sequences, Nova Science










































































![{\displaystyle \operatorname {E} \left(X^{n}\right)=i^{-n}\,\varphi _{X}^{(n)}(0)=i^{-n}\,\left[{\frac {d^{n}}{dt^{n}}}\varphi _{X}(t)\right]_{t=0}.\,\!}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/6e6b4080fec36ab7150198da6f2dc65061c27e7d)






























