Трилистник (узел): различия между версиями
| [непроверенная версия] | [непроверенная версия] |
Kaganer (обсуждение | вклад) м исправление |
MorganBot (обсуждение | вклад) м орфо, replaced: Серебрянное → Серебряное |
||
| (не показаны 2 промежуточные версии 2 участников) | |||
| Строка 29: | Строка 29: | ||
'''Трилистник''' (или '''узел-трилистник''', {{lang-en|trefoil knot}}) — общее название для двух простейших нетривиальных [[Узел (топология)|узлов]]. Левый и правый трилистники – единственные узлы, допускающие [[Диаграмма узла|диаграмму]] с тремя перекрёстками, при том, что любая диаграмма с меньшим числом перекрёстков представляет [[тривиальный узел]]{{sfn|Сосинский А. Б.|2005}}. |
'''Трилистник''' (или '''узел-трилистник''', {{lang-en|trefoil knot}}) — общее название для двух простейших нетривиальных [[Узел (топология)|узлов]]. Левый и правый трилистники – единственные узлы, допускающие [[Диаграмма узла|диаграмму]] с тремя перекрёстками, при том, что любая диаграмма с меньшим числом перекрёстков представляет [[тривиальный узел]]{{sfn|Сосинский А. Б.|2005}}. |
||
Стоит отметить, что в научной литературе по теории узлов нередко можно встретить словосочетание «узел трилистник», которое от случая к случаю может подразумевать и один конкретный трилистник из двух существующих, и пару из двух трилистников с намёком на то, что утверждение, использующее этот термин, справедливо для них обоих, и использование такого определения самого узла, в котором между левым и правым трилистниками в принципе нет никакого различия (существование не обязательно сохраняющего ориентацию гомеоморфизма пар вместо существования объемлющей изотопии в качестве отношения эквивалентности геометрических узлов){{sfn|Rolfsen|2003}}. Более подробно этот терминологический вопрос обсуждается в разделе [[Трилистник (узел)#Определение|«Определение»]]. |
Стоит отметить, что в научной литературе по теории узлов нередко можно встретить словосочетание «узел трилистник», которое от случая к случаю может подразумевать и один конкретный трилистник из двух существующих, и пару из двух трилистников с намёком на то, что утверждение, использующее этот термин, справедливо для них обоих, и использование такого определения самого узла, в котором между левым и правым трилистниками в принципе нет никакого различия (существование не обязательно сохраняющего ориентацию гомеоморфизма пар вместо существования объемлющей изотопии в качестве отношения эквивалентности геометрических узлов){{sfn|Rolfsen|2003}}. Более подробно этот терминологический вопрос обсуждается в разделе [[Трилистник (узел)#Определение|«Определение»]]. |
||
Левый и правый трилистники являются [[Симметрии узлов|зеркальными образами]] друг друга, а потому обладают очень сходными наборами присущих им свойств. Однако всё же некоторые тонкие [[Инвариант узла|инварианты]], такие как [[многочлен HOMFLY|многочлен HOMFLY-PT]] или {{нп5|Сигнатура узла|сигнатура|en| |
Левый и правый трилистники являются [[Симметрии узлов|зеркальными образами]] друг друга, а потому обладают очень сходными наборами присущих им свойств. Однако всё же некоторые тонкие [[Инвариант узла|инварианты]], такие как [[многочлен HOMFLY|многочлен HOMFLY-PT]] или {{нп5|Сигнатура узла|сигнатура|en| |
||
| Строка 38: | Строка 38: | ||
Трилистники часто возникают в [[хими]]и и [[молекулярная биология|молекулярной биологии]] как форма заузленности [[Молекула|молекул]] (в таких случаях они иногда называются [[Молекулярные узлы|молекулярными]] или органическими трилистниками), являясь в этом виде классическими представителями пересечения абстрактной [[топология|топологии]] с [[Естественные науки|естественными науками]]{{sfn|Ponnuswamy, Cougnon, Clough, Pantoş, Sanders|2012}}{{sfn|Rapenne, Dietrich-Buchecker, Sauvage|1996}}. |
Трилистники часто возникают в [[хими]]и и [[молекулярная биология|молекулярной биологии]] как форма заузленности [[Молекула|молекул]] (в таких случаях они иногда называются [[Молекулярные узлы|молекулярными]] или органическими трилистниками), являясь в этом виде классическими представителями пересечения абстрактной [[топология|топологии]] с [[Естественные науки|естественными науками]]{{sfn|Ponnuswamy, Cougnon, Clough, Pantoş, Sanders|2012}}{{sfn|Rapenne, Dietrich-Buchecker, Sauvage|1996}}. |
||
Кроме того, различные изображения трилистников встречаются на многих артефактах разных культур и эпох – трилистники нередко использовались в качестве [[мистика|мистического]] или [[Религиозные символы|религиозного символа]] (в этом смысле чаще встречаются более локальные и специальные понятия вроде [[трикветр]] или [[валькнут]]), а также в искусстве, например, как составная часть [[Художественная роспись|росписей]], [[узор]]ов или [[Мозаика|мозаик]]. |
Кроме того, различные изображения трилистников встречаются на многих артефактах разных культур и эпох – трилистники нередко использовались в качестве [[мистика|мистического]] или [[Религиозные символы|религиозного символа]] (в этом смысле чаще встречаются более локальные и специальные понятия вроде [[трикветр]] или [[валькнут]]), а также в искусстве, например, как составная часть [[Художественная роспись|росписей]], [[узор]]ов или [[Мозаика|мозаик]]. |
||
В современном мире символ трилистника не менее популярен и различные стилизованные изображения трилистников нередко можно встретить на [[эмблема]]х и [[логотип]]ах, в качестве [[декор]]ативных элементов или в [[произведение искусства|произведениях искусства]]. |
В современном мире символ трилистника не менее популярен и различные стилизованные изображения трилистников нередко можно встретить на [[эмблема]]х и [[логотип]]ах, в качестве [[декор]]ативных элементов или в [[произведение искусства|произведениях искусства]]. |
||
Наряду с [[Кольца Борромео|кольцами Борромео]], [[Зацепление Хопфа|зацеплением Хопфа]], [[Тривиальный узел|тривиальным узлом]] и некоторыми другими понятиями как классической теории узлов, так и топологии в целом, трилистники являются ключевым объектом в изложении и практике спорного{{sfn|Брикмон, Сокал|2002}} [[психоанализ|психоаналитического]] исследования [[философ]]ов [[Лакан, Жак| |
Наряду с [[Кольца Борромео|кольцами Борромео]], [[Зацепление Хопфа|зацеплением Хопфа]], [[Тривиальный узел|тривиальным узлом]] и некоторыми другими понятиями как классической теории узлов, так и топологии в целом, трилистники являются ключевым объектом в изложении и практике спорного{{sfn|Брикмон, Сокал|2002}} [[психоанализ|психоаналитического]] исследования [[философ]]ов [[Лакан, Жак|Жака Лакана]] и [[Вапперо, Жан-Мишель|Жана-Мишеля Вапперо]]{{sfn|Вапперо Ж.-М.|2022}}. |
||
== Определение == |
== Определение == |
||
| Строка 50: | Строка 50: | ||
</gallery> |
</gallery> |
||
Когда речь заходит о трилистниках, в математической литературе обычно даётся одновременно некорректное и [[остенсивное определение]], а именно, приводится изображение одного (правого или левого) трилистника и подпись вида «на этом рисунке изображён узел трилистник»{{sfn|Burde, Zieschang|2013}}{{sfn|Adams|2004}}{{sfn|Rolfsen|2003}}{{sfn|Livingston|1996}}{{sfn|Kawauchi|1996}}. Чаще всего это связано с предполагаемым уровнем знаний читателя – в работах для начинающих излагаемые ниже тонкие детали предполагаются несущественными, а в изданиях для профессионалов – хорошо известными. Кроме того, существует и другая неоднозначность – на рисунке справа (как и везде далее) трилистники называются '''левым''' и '''правым''' в соответствии с обозначениями книги Кунио Мурасуги «Knot Theory & Its Applications» ({{sfn0|Murasugi| 1996}}), однако в этом случае нет общего устоявшегося соглашения о нотации. Так, например, в другом классическом учебнике «Knot theory» Чарльза Ливингстона ({{sfn0|Livingston|1996}}) используются противоположные обозначения{{sfn|Burde, Zieschang|2013|loc=Есть термины «левый» и «правый» трилистник, обозначены противоположно варианту Мурасуги}}{{sfn|Adams|2004|loc=Нет терминов «левый» и «правый» трилистник, левый назван «трилистником» правый – его «отражением»}}{{sfn|Kawauchi|1996|p=|loc=Введены термины «левый» и «правый» трилистники, однако употребляются единожды, а во всех остальных случаях «трилистником» и его «отражением» называются попеременно оба узла}}. |
Когда речь заходит о трилистниках, в математической литературе обычно даётся одновременно некорректное и [[остенсивное определение]], а именно, приводится изображение одного (правого или левого) трилистника и подпись вида «на этом рисунке изображён узел трилистник»{{sfn|Burde, Zieschang|2013}}{{sfn|Adams|2004}}{{sfn|Rolfsen|2003}}{{sfn|Livingston|1996}}{{sfn|Kawauchi|1996}}. Чаще всего это связано с предполагаемым уровнем знаний читателя – в работах для начинающих излагаемые ниже тонкие детали предполагаются несущественными, а в изданиях для профессионалов – хорошо известными. Кроме того, существует и другая неоднозначность – на рисунке справа (как и везде далее) трилистники называются '''левым''' и '''правым''' в соответствии с обозначениями книги Кунио Мурасуги «Knot Theory & Its Applications» ({{sfn0|Murasugi| 1996}}), однако в этом случае нет общего устоявшегося соглашения о нотации. Так, например, в другом классическом учебнике «Knot theory» Чарльза Ливингстона ({{sfn0|Livingston|1996}}) используются противоположные обозначения{{sfn|Burde, Zieschang|2013|loc=Есть термины «левый» и «правый» трилистник, обозначены противоположно варианту Мурасуги}}{{sfn|Adams|2004|loc=Нет терминов «левый» и «правый» трилистник, левый назван «трилистником» правый – его «отражением»}}{{sfn|Kawauchi|1996|p=|loc=Введены термины «левый» и «правый» трилистники, однако употребляются единожды, а во всех остальных случаях «трилистником» и его «отражением» называются попеременно оба узла}}. |
||
Конечно, в случае определения с помощью рисунка, всегда подразумевается, что соответствующим трилистником называется любой геометрический узел, объемлюще-изотопный геометрическому узлу, образ которого изображён на рисунке, а также соответствующий объемлюще-изотопический класс. |
Конечно, в случае определения с помощью рисунка, всегда подразумевается, что соответствующим трилистником называется любой геометрический узел, объемлюще-изотопный геометрическому узлу, образ которого изображён на рисунке, а также соответствующий объемлюще-изотопический класс. |
||
| Строка 65: | Строка 65: | ||
Кроме того, нетривиальным результатом является и то, что подобная терминология в принципе осмыслена, а левый и правый трилистники — действительно различные нетривиальные узлы, то есть являются несовпадающими объемлюще-изотопическими классами геометрических узлов. Впервые этот результат получил{{sfn|Dehn|1914}} [[Ден, Макс|Макс Ден]] в 1914 году, исследуя введенную им в этой же работе [[Группа узла|группу узла]] вместе с так называемой «периферической системой» в виде меридиана и параллели, однако со временем появились и другие, менее трудоёмкие способы различить два трилистника, к примеру [[Трёхцветная раскраска|раскраски узлов]] или [[Многочлен HOMFLY|полиномиальные инварианты]]{{sfn|Burde, Zieschang|2013|p=322}}. |
Кроме того, нетривиальным результатом является и то, что подобная терминология в принципе осмыслена, а левый и правый трилистники — действительно различные нетривиальные узлы, то есть являются несовпадающими объемлюще-изотопическими классами геометрических узлов. Впервые этот результат получил{{sfn|Dehn|1914}} [[Ден, Макс|Макс Ден]] в 1914 году, исследуя введенную им в этой же работе [[Группа узла|группу узла]] вместе с так называемой «периферической системой» в виде меридиана и параллели, однако со временем появились и другие, менее трудоёмкие способы различить два трилистника, к примеру [[Трёхцветная раскраска|раскраски узлов]] или [[Многочлен HOMFLY|полиномиальные инварианты]]{{sfn|Burde, Zieschang|2013|p=322}}. |
||
Хотя визуальное определение и является наиболее распространённым, существует ряд и более аккуратных эквивалентных определений, пусть и задействующих некоторые дополнительные концепции. |
Хотя визуальное определение и является наиболее распространённым, существует ряд и более аккуратных эквивалентных определений, пусть и задействующих некоторые дополнительные концепции. |
||
=== Косы === |
=== Косы === |
||
| Строка 75: | Строка 75: | ||
=== Торические узлы=== |
=== Торические узлы=== |
||
<gallery mode="packed" heights="300px" style=" float:right; clear:right; "> |
<gallery mode="packed" heights="300px" style=" float:right; clear:right; "> |
||
Righthanded trefoil embedded in the torus.png | Правый трилистник, вложенный в [[Тор (поверхность) |
Righthanded trefoil embedded in the torus.png | Правый трилистник, вложенный в [[Тор (поверхность)|тор]] |
||
</gallery> |
</gallery> |
||
Правым трилистником называется [[торический узел]] <math>\textrm{T}(2,3)</math>. Иными словами, правым трилистником называется любой геометрический узел, объемлюще изотопный простой замкнутой кривой в <math>\mathbb{R}^3\subset\mathbb{R}^3\cup\{\infty\}\cong S^3</math>, заданной параметрически как |
Правым трилистником называется [[торический узел]] <math>\textrm{T}(2,3)</math>. Иными словами, правым трилистником называется любой геометрический узел, объемлюще изотопный простой замкнутой кривой в <math>\mathbb{R}^3\subset\mathbb{R}^3\cup\{\infty\}\cong S^3</math>, заданной параметрически как |
||
| Строка 108: | Строка 108: | ||
В каждом из приведённых выше случаев левый трилистник можно определить либо по аналогии, заменяя соответствующие знаки на противоположные, либо как зеркальный образ правого трилистника по определению. |
В каждом из приведённых выше случаев левый трилистник можно определить либо по аналогии, заменяя соответствующие знаки на противоположные, либо как зеркальный образ правого трилистника по определению. |
||
Кроме того, заметим, что иногда термин «трилистник» всё таки имеет место быть без дополнительных уточнений. Дело в том, что всё изложенное выше (и далее) подразумевает работу с определением узла, основанном на понятии объемлющей изотопии. Существует также и эквивалентное этому определение, где под узлом также понимается некоторый класс эквивалентности геометрических узлов, но два геометрических узла теперь называются эквивалентными, если существует соответствующий [[гомеоморфизм]] пар (образ узла, [[трёхмерная сфера]]), переводящий образ одного геометрического узла в образ другого и сохраняющий [[ориентация|ориентацию]] трёхмерной сферы{{sfn|Rolfsen|2003}}. Однако в некоторых работах условие сохранения ориентации опускается, в связи с чем, оказывается допустимым гомеоморфизм, реализующий зеркальное отражение. Иными словами, в определении, не учитывающем сохранение ориентации, узел и его зеркальный образ являются одним и тем же узлом по определению. В частности, в таком определении левый и правый трилистники ничем не различаются и корректно использование одного слова для указания на любой из них. Но в связи с тем, что такое определение хоть и удобно для пользования в свете определенных задач и вопросов, но утрачивает достаточно широкий круг деталей, всё изложение настоящей статьи производится в объемлюще-изотопическом смысле. |
Кроме того, заметим, что иногда термин «трилистник» всё таки имеет место быть без дополнительных уточнений. Дело в том, что всё изложенное выше (и далее) подразумевает работу с определением узла, основанном на понятии объемлющей изотопии. Существует также и эквивалентное этому определение, где под узлом также понимается некоторый класс эквивалентности геометрических узлов, но два геометрических узла теперь называются эквивалентными, если существует соответствующий [[гомеоморфизм]] пар (образ узла, [[трёхмерная сфера]]), переводящий образ одного геометрического узла в образ другого и сохраняющий [[ориентация|ориентацию]] трёхмерной сферы{{sfn|Rolfsen|2003}}. Однако в некоторых работах условие сохранения ориентации опускается, в связи с чем, оказывается допустимым гомеоморфизм, реализующий зеркальное отражение. Иными словами, в определении, не учитывающем сохранение ориентации, узел и его зеркальный образ являются одним и тем же узлом по определению. В частности, в таком определении левый и правый трилистники ничем не различаются и корректно использование одного слова для указания на любой из них. Но в связи с тем, что такое определение хоть и удобно для пользования в свете определенных задач и вопросов, но утрачивает достаточно широкий круг деталей, всё изложение настоящей статьи производится в объемлюще-изотопическом смысле. |
||
== Свойства == |
== Свойства == |
||
| Строка 115: | Строка 115: | ||
*Правый и левый трилистники – единственные узлы, допускающие диаграмму с тремя перекрёстками, причем в обоих случаях эта диаграмма [[Диаграмма узла|минимальна]]. Иначе говоря, трилистники – единственные узлы с [[Число пересечений (теория узлов)|числом перекрёстков]] равным <math>3</math>. |
*Правый и левый трилистники – единственные узлы, допускающие диаграмму с тремя перекрёстками, причем в обоих случаях эта диаграмма [[Диаграмма узла|минимальна]]. Иначе говоря, трилистники – единственные узлы с [[Число пересечений (теория узлов)|числом перекрёстков]] равным <math>3</math>. |
||
*Правый и левый трилистники являются [[Рациональный узел|рациональными]] (или двумостовыми) узлами с дробями <math>-\tfrac{3}{2}</math> и <math>\tfrac{3}{2}</math> соответственно. |
*Правый и левый трилистники являются [[Рациональный узел|рациональными]] (или двумостовыми) узлами с дробями <math>-\tfrac{3}{2}</math> и <math>\tfrac{3}{2}</math> соответственно. |
||
* Оба трилистника являются [[Альтернированный узел|альтернированными]] узлами. |
* Оба трилистника являются [[Альтернированный узел|альтернированными]] узлами. |
||
[[Файл:Unknotting trefoil.png|мини|350px|Правый трилистник превращается в тривиальный узел за одно переключение перекрёстков.]] |
[[Файл:Unknotting trefoil.png|мини|350px|Правый трилистник превращается в тривиальный узел за одно переключение перекрёстков.]] |
||
| Строка 125: | Строка 123: | ||
* Оба трилистника имеют [[число отрезков]], равное <math>6</math>, причём это наименьшее значение, которое принимает число отрезков на нетривиальных узлах. Кроме того, трилистники – единственные узлы с таким числом отрезков{{sfn|Jin|1997}}. |
* Оба трилистника имеют [[число отрезков]], равное <math>6</math>, причём это наименьшее значение, которое принимает число отрезков на нетривиальных узлах. Кроме того, трилистники – единственные узлы с таким числом отрезков{{sfn|Jin|1997}}. |
||
* Оба трилистника имеют [[индекс косы]] равный <math>2</math>, так как правый трилистник можно определить как замыкание Александера косы <math>\sigma^3</math> с двумя нитями, а левый – как замыкание Александера косы <math>\sigma^{-3}</math> с двумя нитями, а индекс косы нетривиального узла всегда больше или равен <math>2</math>. |
* Оба трилистника имеют [[индекс косы]] равный <math>2</math>, так как правый трилистник можно определить как замыкание Александера косы <math>\sigma^3</math> с двумя нитями, а левый – как замыкание Александера косы <math>\sigma^{-3}</math> с двумя нитями, а индекс косы нетривиального узла всегда больше или равен <math>2</math>. |
||
[[Файл:Tricoloring.png|мини|180px|Левый трилистник, правильно [[Трёхцветная раскраска|раскрашенный в три цвета.]]]] |
[[Файл:Tricoloring.png|мини|180px|Левый трилистник, правильно [[Трёхцветная раскраска|раскрашенный в три цвета.]]]] |
||
* Оба трилистника являются [[Трёхцветная раскраска|<math>3</math>-раскрашиваемыми]]. |
* Оба трилистника являются [[Трёхцветная раскраска|<math>3</math>-раскрашиваемыми]]. |
||
| ⚫ | * Любой узел за конечное количество [[пасс-мув]]ов можно преобразовать либо в тривиальный узел, либо в один из трилистников, причем трилистники тоже можно преобразовать друг в друга за конечное число пасс-мувов. Однако тривиальный узел нельзя преобразовать ни в левый, ни в правый трилистник за конечное число пасс-мувов. Более точно, [[гордиев граф]] преобразования пасс-мув имеет две [[Компонента связности|компоненты связности]], в одной содержится [[тривиальный узел]], а в другой – оба трилистника. Если вершина гордиева графа пасс-мува, соответствующая некоторому данному узлу, в лежит в компоненте связности тривиального узла, то [[Инвариант Арфа узла|инвариант Арфа]] этого узла равен <math>0</math>, а если в компоненте трилистников, то <math>1</math>. Следовательно, оба трилистника имеют инвариант Арфа, равный <math>1</math>. Это замечание, в частности, можно рассматривать как эквивалентное определение инварианта Арфа{{sfn|Kauffman|1987|p=74-78}}. |
||
| ⚫ | * Любой узел за конечное количество [[ |
||
* Левый и правый трилистники не допускают зеркального сглаживания или, иначе говоря, не являются зеркально косметически эквивалентными. Это означает, что ни одна диаграмма правого трилистника не имеет такого перекрёстка, [[Разрешение перекрёстка|разрешение]] (сглаживание) которого бы дало диаграмму левого трилистника (и наоборот). Иными словами, в гордиевом графе [[H(2)-мув|<math>\textrm{H}(2)</math>-мува]] нет ребра, соединяющего трилистники{{sfn|Livingston|2020}}. |
* Левый и правый трилистники не допускают зеркального сглаживания или, иначе говоря, не являются зеркально косметически эквивалентными. Это означает, что ни одна диаграмма правого трилистника не имеет такого перекрёстка, [[Разрешение перекрёстка|разрешение]] (сглаживание) которого бы дало диаграмму левого трилистника (и наоборот). Иными словами, в гордиевом графе [[H(2)-мув|<math>\textrm{H}(2)</math>-мува]] нет ребра, соединяющего трилистники{{sfn|Livingston|2020}}. |
||
[[Файл:TricoloredGrannyKnot.svg|мини|180px|Связная сумма двух левых трилистников, [[Трёхцветная раскраска|правильно раскрашенная в три цвета.]] Этот узел нельзя превратить в тривиальный с помощью одного переключения перекрёстков или одного <math>\textrm{H(2)}</math>-мува.]] |
[[Файл:TricoloredGrannyKnot.svg|мини|180px|Связная сумма двух левых трилистников, [[Трёхцветная раскраска|правильно раскрашенная в три цвета.]] Этот узел нельзя превратить в тривиальный с помощью одного переключения перекрёстков или одного <math>\textrm{H(2)}</math>-мува.]] |
||
* Если <math>K^n</math> – узел, являющийся [[Связная сумма |
* Если <math>K^n</math> – узел, являющийся [[Связная сумма узлов|связной суммой]] <math>n</math> узлов, каждый из которых либо левый, либо правый трилистник, то его число развязывания и [[H(2)-число развязывания|<math>\textrm{H}(2)</math>-число развязывания]] равны в точности <math>n</math> исходя из гомологической оценки Хоста-Наканиши-Таниямы. В частности, из этого факта следует, что гордиевы графы переключения перекрёстков и <math>\textrm{H}(2)</math>-мува имеют бесконечный [[Диаметр графа|диаметр]]{{sfn|Hoste, Nakanishi, Taniyama|1990}}. |
||
=== Топологические === |
=== Топологические === |
||
[[Файл:Superfície - bordo trifólio.jpg|мини|180px|Поверхность Зейферта левого трилистника.]] |
[[Файл:Superfície - bordo trifólio.jpg|мини|180px|Поверхность Зейферта левого трилистника.]] |
||
* [[Дополнение узла|Дополнения]] трилистников [[Гомеоморфизм|гомеоморфны]] (так как отражение является гомеоморфизмом). Оба трилистника имеют [[Группа узла|группу узла]], допускающую [[Задание группы|копредставление]] <math>\langle x ,y \mid x^2 = y^3 \rangle</math>. Другое копредставление этой же группы <math>\langle x, y \mid xyx = yxy \rangle</math> говорит об [[Изоморфизм|изоморфности]] этой группы [[Группа кос|группе кос]] с тремя нитями. Эта связь объясняется [[Гомотопическая эквивалентность|гомотопической эквивалентностью]] [[Конфигурационное пространство|конфигурационного пространства]] <math>\textrm{UConf}_3(\mathbb{R^2})</math> трёх различных неупорядоченных точек на [[Плоскость (математика)|плоскости]] и [[Внутренность |
* [[Дополнение узла|Дополнения]] трилистников [[Гомеоморфизм|гомеоморфны]] (так как отражение является гомеоморфизмом). Оба трилистника имеют [[Группа узла|группу узла]], допускающую [[Задание группы|копредставление]] <math>\langle x ,y \mid x^2 = y^3 \rangle</math>. Другое копредставление этой же группы <math>\langle x, y \mid xyx = yxy \rangle</math> говорит об [[Изоморфизм|изоморфности]] этой группы [[Группа кос|группе кос]] с тремя нитями. Эта связь объясняется [[Гомотопическая эквивалентность|гомотопической эквивалентностью]] [[Конфигурационное пространство|конфигурационного пространства]] <math>\textrm{UConf}_3(\mathbb{R^2})</math> трёх различных неупорядоченных точек на [[Плоскость (математика)|плоскости]] и [[Внутренность|внутренности]] дополнения трилистников. <!--- пример в статье группа узла квандл ---> |
||
| ⚫ | *[[Разветвлённое накрытие|<math>n</math>-листное разветвлённое накрытие]] <math>S^3</math>, разветвлённое в правом трилистнике, гомеоморфно <math>n</math>-листному разветвлённому накрытию <math>S^3</math>, разветвлённому в левом трилистнике, и обычно обозначается через <math>\Sigma_n(3_1)</math>. Эти пространства исследованы достаточно подробно, в частности, известны их [[Фундаментальная группа|фундаментальные группы]] и [[Гомологии|группы гомологий]]{{sfn|Mulazzani, Vesnin |2001}}. Так, при учёте обозначения <math>d=\textrm{gcd}(n,3),</math> справедливо следующее, |
||
| ⚫ | *[[Разветвлённое накрытие|<math>n</math>-листное разветвлённое накрытие]] <math>S^3</math>, разветвлённое в правом трилистнике, гомеоморфно <math>n</math>-листному разветвлённому накрытию <math>S^3</math>, разветвлённому в левом трилистнике, и обычно обозначается через <math>\Sigma_n(3_1)</math>. Эти пространства исследованы достаточно подробно, в частности, известны их [[Фундаментальная группа|фундаментальные группы]] и [[Гомологии|группы гомологий]]{{sfn|Mulazzani, Vesnin |2001}}. Так, при учёте обозначения <math>d=\textrm{gcd}(n,3),</math> справедливо следующее, |
||
:<math>\textrm{H}_1(\Sigma_n(3_1))\cong\begin{cases}\mathbb{Z}^{d-1}\oplus\mathbb{Z}_{3/d}\,\,\,\,\text{если}\,\, n\,\,\text{чётно},\\ |
:<math>\textrm{H}_1(\Sigma_n(3_1))\cong\begin{cases}\mathbb{Z}^{d-1}\oplus\mathbb{Z}_{3/d}\,\,\,\,\text{если}\,\, n\,\,\text{чётно},\\ |
||
\mathbb{Z}^{d-1}_2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{если}\,\, n \,\,\text{нечётно}.\end{cases}</math> |
\mathbb{Z}^{d-1}_2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{если}\,\, n \,\,\text{нечётно}.\end{cases}</math> |
||
:Некоторые из этих разветвлённых накрытий обладают необычными свойствами или являются особенными примечательными [[Многообразие|многообразиями]]. Так, например, |
:Некоторые из этих разветвлённых накрытий обладают необычными свойствами или являются особенными примечательными [[Многообразие|многообразиями]]. Так, например, |
||
::* двулистное накрытие <math>\Sigma_2(3_1)</math> гомеоморфно [[Линзовое пространство|линзовому пространству]] <math>\textrm{L}(3,1)</math>{{sfn|Rolfsen|2003|p=304}}, |
::* двулистное накрытие <math>\Sigma_2(3_1)</math> гомеоморфно [[Линзовое пространство|линзовому пространству]] <math>\textrm{L}(3,1)</math>{{sfn|Rolfsen|2003|p=304}}, |
||
::* фундаментальная группа <math>\pi_1(\Sigma_3(3_1))</math> трёхлистного накрытия изоморфна [[Группа кватернионов|группе кватернионов]]{{sfn|Rolfsen|2003|p=305}}, |
::* фундаментальная группа <math>\pi_1(\Sigma_3(3_1))</math> трёхлистного накрытия изоморфна [[Группа кватернионов|группе кватернионов]]{{sfn|Rolfsen|2003|p=305}}, |
||
::* фундаментальная группа <math>\pi_1(\Sigma_4(3_1))</math> четырёхлистного накрытия изоморфна [[Бинарная группа тетраэдра|бинарной группе тетраэдра]]{{sfn|Rolfsen|2003|p=306}}, |
::* фундаментальная группа <math>\pi_1(\Sigma_4(3_1))</math> четырёхлистного накрытия изоморфна [[Бинарная группа тетраэдра|бинарной группе тетраэдра]]{{sfn|Rolfsen|2003|p=306}}, |
||
| Строка 162: | Строка 156: | ||
* Оба трилистника имеют [[род узла|род]], равный <math>1</math>. |
* Оба трилистника имеют [[род узла|род]], равный <math>1</math>. |
||
* Оба трилистника имеют [[туннельное число]], равное <math>1</math>{{sfn| Morimoto |2016}}. |
* Оба трилистника имеют [[туннельное число]], равное <math>1</math>{{sfn| Morimoto |2016}}. |
||
| ⚫ | |||
| ⚫ | |||
* Оба трилистника являются [[Расслоенный узел|расслоенными узлами]]{{sfn|Rolfsen|2003|p=327|loc=Глава «Fibering the complement of a trefoil»}}. <!--- Глава про расслоенность в Рольфсене ---> |
* Оба трилистника являются [[Расслоенный узел|расслоенными узлами]]{{sfn|Rolfsen|2003|p=327|loc=Глава «Fibering the complement of a trefoil»}}. <!--- Глава про расслоенность в Рольфсене ---> |
||
| ⚫ | * Правый трилистник используется для построения [[Многообразие Черна|многообразия Черна]]. Говоря более подробно, правый трилистник с [[Узел (математика)|оснащением]] <math>1</math> задаёт приклеивание четырёхмерной [[Исчисление Кёрби|<math>2</math>-ручки]] к [[Четырёхмерный шар|четырёхмерному шару]]. Получающееся после приклеивания [[Четырёхмерное многообразие|<math>4</math>-многообразие]] обычно называют [[След узла|<math>1</math>-следом]] правого трилистника. [[Трёхмерное многообразие]], являющееся [[Край многообразия|границей]] <math>1</math>-следа правого трилистника, является [[Гомологическая сфера|гомологической сферой]], а значит, по результату Михаэля Фридмана, ограничивает [[Стягиваемое пространство|топологически стягиваемое]] <math>4</math>-многообразие <math>\Delta^4</math>. Тогда многообразие Черна определяется как склейка по границе <math>1</math>-следа правого трилистника и многообразия <math>\Delta^4</math>{{sfn|Freedman|1982}}. |
||
| ⚫ | * Правый трилистник используется для построения [[Многообразие Черна|многообразия Черна]]. Говоря более подробно, правый трилистник с [[Узел (математика)|оснащением]] <math>1</math> задаёт приклеивание четырёхмерной [[Исчисление Кёрби|<math>2</math>-ручки]] к [[Четырёхмерный шар|четырёхмерному шару]]. Получающееся после приклеивания [[Четырёхмерное многообразие|<math>4</math>-многообразие]] обычно называют [[След узла|<math>1</math>-следом]] правого трилистника. [[Трёхмерное многообразие]], являющееся [[Край многообразия |
||
* Луис Мозер получил полное описание всех возможных пространств, которые получаются из [[Трёхмерная сфера|трёхмерной сферы]] [[Хирургия Дена|хирургией Дена]] с коэффициентом <math>(p, q)</math> по [[Торический узел|торическому узлу]] <math>\textrm{T}(a, b)</math>, то есть, в частности и по трилистникам{{sfn|Sullivan|2013}}. |
* Луис Мозер получил полное описание всех возможных пространств, которые получаются из [[Трёхмерная сфера|трёхмерной сферы]] [[Хирургия Дена|хирургией Дена]] с коэффициентом <math>(p, q)</math> по [[Торический узел|торическому узлу]] <math>\textrm{T}(a, b)</math>, то есть, в частности и по трилистникам{{sfn|Sullivan|2013}}. |
||
=== Геометрические === |
=== Геометрические === |
||
* Оба трилистника имеют [[дуговой индекс]], равный <math>5</math>, и допускают [[n-страничное представление узла|<math>3</math>-страничное представление]]{{sfn|KnotInfo|2004}}{{sfn|Dynnikov|2000}}. |
* Оба трилистника имеют [[дуговой индекс]], равный <math>5</math>, и допускают [[n-страничное представление узла|<math>3</math>-страничное представление]]{{sfn|KnotInfo|2004}}{{sfn|Dynnikov|2000}}. |
||
*Правый и левый трилистники являются [[Торический узел|торическими узлами]] <math>\textrm{T}(2,3)</math> и <math>\textrm{T}(2,-3)</math> соответственно. |
*Правый и левый трилистники являются [[Торический узел|торическими узлами]] <math>\textrm{T}(2,3)</math> и <math>\textrm{T}(2,-3)</math> соответственно. |
||
<!--- *Лежандровы??? ---> |
<!--- *Лежандровы??? ---> |
||
| Строка 182: | Строка 170: | ||
* Оба трилистника являются [[Простой узел (теория узлов)|простыми узлами]] (например, так как трилистники имеют род <math>1</math>, а род аддитивен относительно связного суммирования). |
* Оба трилистника являются [[Простой узел (теория узлов)|простыми узлами]] (например, так как трилистники имеют род <math>1</math>, а род аддитивен относительно связного суммирования). |
||
* Правый трилистник имеет [[Сигнатура узла|сигнатуру]], равную <math>-2</math>, а левый – равную <math>2</math>. Оба трилистника имеют [[Детерминант узла|детерминант]], равный <math>3</math>{{sfn|Rolfsen|2003|p=220}}{{sfn|Burde, Zieschang|2013|p=243}}. |
* Правый трилистник имеет [[Сигнатура узла|сигнатуру]], равную <math>-2</math>, а левый – равную <math>2</math>. Оба трилистника имеют [[Детерминант узла|детерминант]], равный <math>3</math>{{sfn|Rolfsen|2003|p=220}}{{sfn|Burde, Zieschang|2013|p=243}}. |
||
| Строка 197: | Строка 184: | ||
Оба трилистника являются [[Симметрии узлов|двусторонними узлами]], иначе говоря: |
Оба трилистника являются [[Симметрии узлов|двусторонними узлами]], иначе говоря: |
||
* Оба трилистника являются [[Симметрии узлов|обратимыми узлами]], то есть два геометрических узла, представляющих объемлюще-изотопический класс правого трилистника, с введёнными на них противоположным образом [[ |
* Оба трилистника являются [[Симметрии узлов|обратимыми узлами]], то есть два геометрических узла, представляющих объемлюще-изотопический класс правого трилистника, с введёнными на них противоположным образом [[ориентация]]ми являются объемлюще-изотопными с сохранением ориентации, то есть в процессе объемлющей изотопии один ориентированный геометрический узел переходит в другой таким образом, что в итоге совпадут не только их образы, но и ориентации (аналогично для левого). Кроме того, оба трилистника являются [[Симметрии узлов|строго обратимыми]]. |
||
* Оба трилистника являются [[Симметрии узлов|хиральными]] узлами, то есть правый трилистник и его [[Симметрии узлов|зеркальный образ]] (левый трилистник) являются несовпадающими объемлюще-изотопическими классами геометрических узлов (аналогично для левого). |
* Оба трилистника являются [[Симметрии узлов|хиральными]] узлами, то есть правый трилистник и его [[Симметрии узлов|зеркальный образ]] (левый трилистник) являются несовпадающими объемлюще-изотопическими классами геометрических узлов (аналогично для левого). |
||
| Строка 220: | Строка 206: | ||
== Классификация == |
== Классификация == |
||
В теории узлов трилистник является первым нетривиальным узлом и единственным узлом с [[Число пересечений (теория узлов)|числом пересечений]] три. Он является [[Простой узел (топология)|простым]] и перечислен с под номером 3<sub>1</sub> в [[Нотация Александера-Бриггса|нотации Александера-Бриггса]]. {{не переведено 5|Нотация Даукера|Нотация Даукера||Dowker notation}} для трилистника — 4 6 2, а [[Нотация Конвея для узлов|нотация Конвея]] трилистника — [3]. |
В теории узлов трилистник является первым нетривиальным узлом и единственным узлом с [[Число пересечений (теория узлов)|числом пересечений]] три. Он является [[Простой узел (топология)|простым]] и перечислен с под номером 3<sub>1</sub> в [[Нотация Александера-Бриггса|нотации Александера-Бриггса]]. {{не переведено 5|Нотация Даукера|Нотация Даукера||Dowker notation}} для трилистника — 4 6 2, а [[Нотация Конвея для узлов|нотация Конвея]] трилистника — [3]. |
||
Трилистник является [[Альтернированный узел|альтернированным узлом]]. Однако, он не является [[Срезанный узел|срезанным узлом]], что означает, что он не ограничивает 2-мерный диск на 4-мерной сфере. Чтобы это показать, следует заметить, что его {{не переведено 5|Сигнатура узла|сигнатура||signature of a knot}} ненулевая. Другое доказательство — многочлен Александера не удовлетворяет [[Срезанный узел|условию Фокса — Милнора]]. |
Трилистник является [[Альтернированный узел|альтернированным узлом]]. Однако, он не является [[Срезанный узел|срезанным узлом]], что означает, что он не ограничивает 2-мерный диск на 4-мерной сфере. Чтобы это показать, следует заметить, что его {{не переведено 5|Сигнатура узла|сигнатура||signature of a knot}} ненулевая. Другое доказательство — многочлен Александера не удовлетворяет [[Срезанный узел|условию Фокса — Милнора]]. |
||
| Строка 229: | Строка 213: | ||
== Инварианты == |
== Инварианты == |
||
[[Многочлен Александера]] трилистника есть |
[[Многочлен Александера]] трилистника есть |
||
| Строка 273: | Строка 256: | ||
<gallery mode=packed heights=150px> |
<gallery mode=packed heights=150px> |
||
Rila 1 yat glagolitic.jpg|Орнаментальный левый трилистник на странице Паренесиса Ефрема Сирина, XI век, [[Библиотека РАН]] |
Rila 1 yat glagolitic.jpg|Орнаментальный левый трилистник на странице Паренесиса Ефрема Сирина, XI век, [[Библиотека РАН]] |
||
U937.jpg|Левый трилистник как элемент [[Уппланд]]ской рунической надписи номер 937, Университетский парк, XI век, [[Уппсала]], [[Швеция]] |
U937.jpg|Левый трилистник как элемент [[Уппланд]]ской рунической надписи номер 937, Университетский парк, XI век, [[Уппсала]], [[Швеция]] |
||
| Строка 281: | Строка 264: | ||
Iron Age to Early Medieval copper alloy mount (FindID 958918).jpg|Крепление из медного сплава в виде левого трилистника, раннее средневековье, 700-1000 годы, найдено в графстве [[Лестершир]], [[Великобритания]] |
Iron Age to Early Medieval copper alloy mount (FindID 958918).jpg|Крепление из медного сплава в виде левого трилистника, раннее средневековье, 700-1000 годы, найдено в графстве [[Лестершир]], [[Великобритания]] |
||
Early Medieval gold mount (FindID 713485).jpg|Золотая оправа в виде левого трилистника, раннее средневековье, 575-700 годы, найдена в графстве [[Норфолк]], [[Великобритания]] |
Early Medieval gold mount (FindID 713485).jpg|Золотая оправа в виде левого трилистника, раннее средневековье, 575-700 годы, найдена в графстве [[Норфолк]], [[Великобритания]] |
||
Jelling-grosses-tier.gif|Левый трилистник на цветной реставрации [[Рунические камни в Еллинге|рунического камня]] [[Харальд I Синезубый|Харальда I Синезубого]], 970-986 годы, [[Еллинг]], [[Дания]] |
Jelling-grosses-tier.gif|Левый трилистник на цветной реставрации [[Рунические камни в Еллинге|рунического камня]] [[Харальд I Синезубый|Харальда I Синезубого]], 970-986 годы, [[Еллинг]], [[Дания]] |
||
| Строка 287: | Строка 270: | ||
Post-medieval copper-alloy wire composite button (FindID 984790).jpg| Пост-средневековая медная пуговица в виде левого трилистника, 1500-1600 годы, найдена в графстве [[Норфолк]], [[Великобритания]] |
Post-medieval copper-alloy wire composite button (FindID 984790).jpg| Пост-средневековая медная пуговица в виде левого трилистника, 1500-1600 годы, найдена в графстве [[Норфолк]], [[Великобритания]] |
||
Carndonagh Marigold Stone East Face Centre Panel 2016 09 05.jpg| Левый трилистник на центральной панели восточной грани камня Календулы, 730-e годы, [[Карндона]], графство [[Донегол]], провинция [[Ольстер]], [[Ирландия]] |
Carndonagh Marigold Stone East Face Centre Panel 2016 09 05.jpg| Левый трилистник на центральной панели восточной грани камня Календулы, 730-e годы, [[Карндона]], графство [[Донегол]], провинция [[Ольстер]], [[Ирландия]] |
||
Mjollnir.png| Левый трилистник на позолоченном серебряном амулете в виде молота [[Тор (бог)|бога Тора]] – [[Мьёльнир]]а, найден в городке Бредсеттра на острове [[Эланд]], [[Швеция]] |
Mjollnir.png| Левый трилистник на позолоченном серебряном амулете в виде молота [[Тор (бог)|бога Тора]] – [[Мьёльнир]]а, найден в городке Бредсеттра на острове [[Эланд]], [[Швеция]] |
||
| Строка 318: | Строка 301: | ||
Altar, Holy Trinity Church, Blythburgh - geograph.org.uk - 776121.jpg|Зацепление из правого трилистника и тривиального узла на [[Алтарь|алтаре]] церкви Святой Троицы, деревня Блитбург, графство [[Суффолк]], [[Великобритания]] |
Altar, Holy Trinity Church, Blythburgh - geograph.org.uk - 776121.jpg|Зацепление из правого трилистника и тривиального узла на [[Алтарь|алтаре]] церкви Святой Троицы, деревня Блитбург, графство [[Суффолк]], [[Великобритания]] |
||
Pulpit in Christchurch Priory.jpg|Двукомпонентное зацепление из правого трилистника и тривиального узла на кафедре в монастыре города [[Крайстчерч (Дорсет)|Крайстчёрч]], графство [[Дорсет]], [[Великобритания]] |
Pulpit in Christchurch Priory.jpg|Двукомпонентное зацепление из правого трилистника и тривиального узла на кафедре в монастыре города [[Крайстчерч (Дорсет)|Крайстчёрч]], графство [[Дорсет]], [[Великобритания]] |
||
| Строка 350: | Строка 332: | ||
T Barny with his sculpture VALKYRE - 'Norse Maiden Warrior'.jpg| Скульптура «VALKYRE» в виде правого трилистника и её автор, американский скульптор T Barny |
T Barny with his sculpture VALKYRE - 'Norse Maiden Warrior'.jpg| Скульптура «VALKYRE» в виде правого трилистника и её автор, американский скульптор T Barny |
||
Rila 1 yat glagolitic.jpg|Орнаментальный левый трилистник на странице Паренесиса Ефрема Сирина, XI век, [[Библиотека РАН]] |
Rila 1 yat glagolitic.jpg|Орнаментальный левый трилистник на странице Паренесиса Ефрема Сирина, XI век, [[Библиотека РАН]] |
||
U937.jpg|Левый трилистник как элемент [[Уппланд]]ской рунической надписи номер 937, Университетский парк, XI век, [[Уппсала]], [[Швеция]] |
U937.jpg|Левый трилистник как элемент [[Уппланд]]ской рунической надписи номер 937, Университетский парк, XI век, [[Уппсала]], [[Швеция]] |
||
| Строка 358: | Строка 340: | ||
Interior of the church of Maulbronn Monastery Kapitell mit Dreipassknoten - Interlaced triquetra.jpg|Левый трилистник на капители [[Маульброннский монастырь|Маульброннского монастыря]], 1147 год, [[Германия]] |
Interior of the church of Maulbronn Monastery Kapitell mit Dreipassknoten - Interlaced triquetra.jpg|Левый трилистник на капители [[Маульброннский монастырь|Маульброннского монастыря]], 1147 год, [[Германия]] |
||
Nocturnal (instrument).jpg|Двукомпонентное зацепление из левого трилистника и тривиального узла на [[ |
Nocturnal (instrument).jpg|Двукомпонентное зацепление из левого трилистника и тривиального узла на [[ноктурлабиум]]е |
||
Carolingian art in Carinthia, Stiftsmuseum Millstatt, Kärnten.jpg| Каролингское плетение в форме правого трилистника (самый верхний экспонат), музей аббатства Мильштатт, [[Каринтия]], [[Австрия]] |
Carolingian art in Carinthia, Stiftsmuseum Millstatt, Kärnten.jpg| Каролингское плетение в форме правого трилистника (самый верхний экспонат), музей аббатства Мильштатт, [[Каринтия]], [[Австрия]] |
||
| Строка 366: | Строка 348: | ||
Trefoil knot lamp at 31c3.jpg|Лампа в виде правого трилистника на [[Всемирный конгресс хакеров|Всемирном конгрессе хакеров]] 31C3 в [[Гамбург]]е, [[Германия]] |
Trefoil knot lamp at 31c3.jpg|Лампа в виде правого трилистника на [[Всемирный конгресс хакеров|Всемирном конгрессе хакеров]] 31C3 в [[Гамбург]]е, [[Германия]] |
||
Early Medieval gold mount (FindID 713485).jpg|Золотая оправа в виде левого трилистника, раннее средневековье, 575-700 годы, найдена в графстве [[Норфолк]], [[Великобритания]] |
Early Medieval gold mount (FindID 713485).jpg|Золотая оправа в виде левого трилистника, раннее средневековье, 575-700 годы, найдена в графстве [[Норфолк]], [[Великобритания]] |
||
"Gothic Rings", 23" x 19", Ervin Somogyi, Luthier.jpg| Правый трилистник в работе по дереву Эрвина Шомоджи, смешение классического [[Япония|японского]] и [[Готика|готического]] стилей |
"Gothic Rings", 23" x 19", Ervin Somogyi, Luthier.jpg| Правый трилистник в работе по дереву Эрвина Шомоджи, смешение классического [[Япония|японского]] и [[Готика|готического]] стилей |
||
| Строка 374: | Строка 356: | ||
Jelling-grosses-tier.gif|Левый трилистник на цветной реставрации [[Рунические камни в Еллинге|рунического камня]] [[Харальд I Синезубый|Харальда I Синезубого]], 970-986 годы, [[Еллинг]], [[Дания]] |
Jelling-grosses-tier.gif|Левый трилистник на цветной реставрации [[Рунические камни в Еллинге|рунического камня]] [[Харальд I Синезубый|Харальда I Синезубого]], 970-986 годы, [[Еллинг]], [[Дания]] |
||
Constantine War Memorial (DSCN0077).jpg| Связная сумма четырёх левых трилистников на военном мемориале, созданном Elkana Symonds, кладбище у церкви [[Святой Константин|Святого Константина]], 900-1300 годы, деревня Константин, район Керриер, графство [[Корнуолл]], [[Великобритания]] |
Constantine War Memorial (DSCN0077).jpg| Связная сумма четырёх левых трилистников на военном мемориале, созданном Elkana Symonds, кладбище у церкви [[Святой Константин|Святого Константина]], 900-1300 годы, деревня Константин, район Керриер, графство [[Корнуолл]], [[Великобритания]] |
||
Altar, Holy Trinity Church, Blythburgh - geograph.org.uk - 776121.jpg|Зацепление из правого трилистника и тривиального узла на [[Алтарь|алтаре]] церкви Святой Троицы, деревня Блитбург, графство [[Суффолк]], [[Великобритания]] |
Altar, Holy Trinity Church, Blythburgh - geograph.org.uk - 776121.jpg|Зацепление из правого трилистника и тривиального узла на [[Алтарь|алтаре]] церкви Святой Троицы, деревня Блитбург, графство [[Суффолк]], [[Великобритания]] |
||
| Строка 380: | Строка 362: | ||
Post-medieval copper-alloy wire composite button (FindID 984790).jpg| Пост-средневековая медная пуговица в виде левого трилистника, 1500-1600 годы, найдена в графстве [[Норфолк]], [[Великобритания]] |
Post-medieval copper-alloy wire composite button (FindID 984790).jpg| Пост-средневековая медная пуговица в виде левого трилистника, 1500-1600 годы, найдена в графстве [[Норфолк]], [[Великобритания]] |
||
Carndonagh Marigold Stone East Face Centre Panel 2016 09 05.jpg| Левый трилистник на центральной панели восточной грани камня Календулы, 730-e годы, [[Карндона]], графство [[Донегол]], провинция [[Ольстер]], [[Ирландия]] |
Carndonagh Marigold Stone East Face Centre Panel 2016 09 05.jpg| Левый трилистник на центральной панели восточной грани камня Календулы, 730-e годы, [[Карндона]], графство [[Донегол]], провинция [[Ольстер]], [[Ирландия]] |
||
Mjollnir.png| Левый трилистник на позолоченном серебряном амулете в виде молота [[Тор (бог)|бога Тора]] – [[Мьёльнир]]а, найден в городке Бредсеттра на острове [[Эланд]], [[Швеция]] |
Mjollnir.png| Левый трилистник на позолоченном серебряном амулете в виде молота [[Тор (бог)|бога Тора]] – [[Мьёльнир]]а, найден в городке Бредсеттра на острове [[Эланд]], [[Швеция]] |
||
| Строка 400: | Строка 382: | ||
Pulpit in Christchurch Priory.jpg|Двукомпонентное зацепление из правого трилистника и тривиального узла на кафедре в монастыре города [[Крайстчерч (Дорсет)|Крайстчёрч]], графство [[Дорсет]], [[Великобритания]] |
Pulpit in Christchurch Priory.jpg|Двукомпонентное зацепление из правого трилистника и тривиального узла на кафедре в монастыре города [[Крайстчерч (Дорсет)|Крайстчёрч]], графство [[Дорсет]], [[Великобритания]] |
||
Finger ring of unknown date (FindID 734930).jpg| |
Finger ring of unknown date (FindID 734930).jpg|Серебряное кольцо в виде правого трилистника, 600-1900 годы, найдено в графстве [[Сомерсет]], [[Великобритания]] |
||
</gallery> |
</gallery> |
||
| Строка 411: | Строка 393: | ||
Coat of arms of Dominic Ryōji Miyahara.svg|Правый трилистник на гербе епископа [[Мияхара, Доминик Рёдзи|Доминика Рёдзи Мияхара]],[[Епархия Фукуоки]], [[Япония]] |
Coat of arms of Dominic Ryōji Miyahara.svg|Правый трилистник на гербе епископа [[Мияхара, Доминик Рёдзи|Доминика Рёдзи Мияхара]],[[Епархия Фукуоки]], [[Япония]] |
||
Coat of arms of Douglas John Lucia.svg|Двукомпонентное зацепление из правого трилистника и тривиального узла на гербе епископа Дугласа Джона Люсии, [[Епархия Сиракьюса]], [[США]] |
Coat of arms of Douglas John Lucia.svg|Двукомпонентное зацепление из правого трилистника и тривиального узла на гербе епископа Дугласа Джона Люсии, [[Епархия Сиракьюса]], [[США]] |
||
Coat of Arms of Alberto Uy.svg|Двукомпонентное зацепление из правого трилистника и тривиального узла на гербе епископа Альберта Уйя, [[Епархия Тагбиларана]], [[Республика Филиппины]] |
Coat of Arms of Alberto Uy.svg|Двукомпонентное зацепление из правого трилистника и тривиального узла на гербе епископа Альберта Уйя, [[Епархия Тагбиларана]], [[Республика Филиппины]] |
||
Coat of arms of Alejandro Dumbrigue Aclan.svg| Левый трилистник на гербе епископа Алехандро Алкана, [[Архиепархия Лос-Анджелеса]], [[США]] |
Coat of arms of Alejandro Dumbrigue Aclan.svg| Левый трилистник на гербе епископа Алехандро Алкана, [[Архиепархия Лос-Анджелеса]], [[США]] |
||
| Строка 429: | Строка 411: | ||
Penny (Triqueta and Raven Banner) of Amlaib Cuaran.png|Правый трилистник на аверсе именной монеты [[Олав III (король Дублина)|Олава III]], короля [[Королевство Йорвик|Йорк]]а, 949-952 годы |
Penny (Triqueta and Raven Banner) of Amlaib Cuaran.png|Правый трилистник на аверсе именной монеты [[Олав III (король Дублина)|Олава III]], короля [[Королевство Йорвик|Йорк]]а, 949-952 годы |
||
Eadberth sceat 737 75001441.jpg| Левый трилистник на именном [[ |
Eadberth sceat 737 75001441.jpg| Левый трилистник на именном [[скеат]]е [[Эдберт]]а, [[король Нортумбрии|короля Нортумбрии]], 737-758 годы |
||
Coin of Ukraine M2000 A.jpg| Правый трилистник на аверсе [[Украина|украинской]] [[Памятная монета|памятной монеты]] из серии [[На рубеже тысячелетий (серия монет)|«На рубеже тысячелетий»]], 2000 год |
Coin of Ukraine M2000 A.jpg| Правый трилистник на аверсе [[Украина|украинской]] [[Памятная монета|памятной монеты]] из серии [[На рубеже тысячелетий (серия монет)|«На рубеже тысячелетий»]], 2000 год |
||
| Строка 451: | Строка 433: | ||
Signal Hill Canadian Whisky Logo.png | Правый трилистник в форме [[валькнут]]а на логотипе [[Канада|канадского]] [[виски]] Signal Hill |
Signal Hill Canadian Whisky Logo.png | Правый трилистник в форме [[валькнут]]а на логотипе [[Канада|канадского]] [[виски]] Signal Hill |
||
SCA company logo.svg |Правый трилистник в форме [[валькнут]]а на логотипе [[Шведское целлюлозное предприятие|Шведского целлюлозного предприятия]] |
SCA company logo.svg |Правый трилистник в форме [[валькнут]]а на логотипе [[Шведское целлюлозное предприятие|Шведского целлюлозного предприятия]] |
||
ATN Bangla.svg | Правильно раскрашенный в три цвета левый трилистник в форме [[валькнут]]а на логотипе [[ |
ATN Bangla.svg | Правильно раскрашенный в три цвета левый трилистник в форме [[валькнут]]а на логотипе [[бангладеш]]ского телеканала ATN Bangla |
||
Logo Hennlich schwarz.png |Левый трилистник в форме [[валькнут]]а на логотипе группы компаний HENNLICH |
Logo Hennlich schwarz.png |Левый трилистник в форме [[валькнут]]а на логотипе группы компаний HENNLICH |
||
Comunn Oiseanach.png |Двукомпонентное зацепление из правого трилистника и тривиального узла на эмблеме [[Оссиан |
Comunn Oiseanach.png |Двукомпонентное зацепление из правого трилистника и тривиального узла на эмблеме [[Оссиан]]ского общества [[Университет Глазго|Университета Глазго]] |
||
Celtic_Knot_2020.svg |Правый трилистник, правильно раскрашенный в три цвета, на эмблеме конференции [[Викимедиа]] по многоязычию Celtic Knot Conference 2020 |
Celtic_Knot_2020.svg |Правый трилистник, правильно раскрашенный в три цвета, на эмблеме конференции [[Викимедиа]] по многоязычию Celtic Knot Conference 2020 |
||
Triodos Bank textlogo.svg | Правый трилистник на логотипе группы [[Нидерланды|нидерладских]] банков [[Триодос Банк]] |
Triodos Bank textlogo.svg | Правый трилистник на логотипе группы [[Нидерланды|нидерладских]] банков [[Триодос Банк]] |
||
</gallery> |
</gallery> |
||
==Абстрактные изображения трилистников == |
|||
[[Файл:Trefoil-non-3-symm.svg|thumb|right|Трилистник с осевой симметрией порядка 2]] |
|||
[[Файл:Trefoil Knot.gif|right|180px]] |
|||
В качестве простейшего нетривиального узла, трилистник является частым [[Мотив (искусство)|мотивом]] в [[Иконография|иконографии]] и [[Изобразительное искусство|изобразительном искусстве]]. |
|||
<gallery> |
|||
Mjollnir.png|Древне­скандинавская подвеска [[мьёльнир]] с трилистником |
|||
Triquetra-Vesica.svg|Простой символ [[трикветр]] |
|||
Triquetra-tightly-knotted.svg|Плотный трикветр |
|||
Valknut-Symbol-triquetra.svg|Немецкий {{не переведено 5|Валкнут|Валкнут||Valknut}} |
|||
Metallic Valknut black background.PNG|Металлический Валкнут в виде трилистника |
|||
ATV News GL5463 and Yau Ma Tei Station exit 20060712.jpg|Трилистник, используемый в Лого {{не переведено 5|ATV Home|aTV ||ATV Home}} |
|||
Superfície - bordo trifólio.jpg|Ориентируемая поверхность, ограниченная трилистником |
|||
Superfície não orientável - Bordo trifólio.jpg|[[Лист Мёбиуса]], ограниченный трилистником |
|||
</gallery> |
|||
Присутствует на современных последних норвежских монетах Харальда Хардроде (1047—1066), для которых этот тройной узел стал наиболее типичным изображением, как правило, заполнявшим поле аверса.<ref name="Керсновский">Керсновский Р. Монета в культуре Средних веков. — пер. с польск. и коммент. канд. ист. наук. Т.Ю. Стукаловой — С. 414 — Москва: 2018 — ISBN: 978-5-89076-320-4</ref> |
|||
Присутствует на западноевропейских монетах, происходящих с каролингских монетных дворов и, особенно, из архиепископских мастерских в Андернахе, Кёльне, Гюи или Страсбурге (531), мотив тройного узла с большой долей вероятности можно считать исключительно символом Святой Троицы.<ref name="Керсновский" /> |
|||
Присутствует на дохристианских монетах в Йорке и Хедебю, и на надгробных камнях VIII—IX вв. на острове Готланд.<ref name="Керсновский" /> |
|||
<!--- |
|||
== См. также == |
|||
* {{не переведено 5|Cписок простых узлов||en|List of prime knots}} |
|||
* [[Список узлов]] |
|||
---> |
|||
== Примечания == |
== Примечания == |
||
{{примечания|2}} |
{{примечания|2}} |
||
| Строка 780: | Строка 734: | ||
|автор = [[Шоу, Джордж Рассел|Shaw G. R.]] |
|автор = [[Шоу, Джордж Рассел|Shaw G. R.]] |
||
|заглавие = Knots: Useful & Ornamental |
|заглавие = Knots: Useful & Ornamental |
||
|ссылка = https://archive.org/details/knotsusefulornam0000shaw_k2s0 |
|||
|nodot = |
|nodot = |
||
|язык = en |
|язык = en |
||
Текущая версия от 12:30, 11 июня 2023
| Трилистник | |
|---|---|
 Левый трилистник | |
| Обозначения | |
| Конвея | [3] |
| Александера–Бриггса[англ.] | 31 |
| Даукера[англ.] | 4, 6, 2 |
| Многочлены | |
| Александера | |
| Джонса |
|
| Кауфмана |
|
| Конвея | |
| HOMFLY |
|
| Инварианты | |
| Инвариант Арфа[англ.] | 1 |
| Длина косы | 3 |
| Число нитей | 2 |
| Число мостов | 2 |
| Число плёнок[англ.] | 1 |
| Число пересечений | 3 |
| Род | 1 |
| Число отрезков | 6 |
| Число туннелей[англ.] | 1 |
| Число развязывания | 1 |
| Свойства | |
| Простой, торический, альтернированный, кружевной, несрезанный, не топологически срезанный, двусторонний, трёхцветный, скрученный, расслоенный | |
Трилистник (или узел-трилистник, англ. trefoil knot) — общее название для двух простейших нетривиальных узлов. Левый и правый трилистники – единственные узлы, допускающие диаграмму с тремя перекрёстками, при том, что любая диаграмма с меньшим числом перекрёстков представляет тривиальный узел[1].
Стоит отметить, что в научной литературе по теории узлов нередко можно встретить словосочетание «узел трилистник», которое от случая к случаю может подразумевать и один конкретный трилистник из двух существующих, и пару из двух трилистников с намёком на то, что утверждение, использующее этот термин, справедливо для них обоих, и использование такого определения самого узла, в котором между левым и правым трилистниками в принципе нет никакого различия (существование не обязательно сохраняющего ориентацию гомеоморфизма пар вместо существования объемлющей изотопии в качестве отношения эквивалентности геометрических узлов)[2]. Более подробно этот терминологический вопрос обсуждается в разделе «Определение».
Левый и правый трилистники являются зеркальными образами друг друга, а потому обладают очень сходными наборами присущих им свойств. Однако всё же некоторые тонкие инварианты, такие как многочлен HOMFLY-PT или сигнатура[англ.], способны установить их формальное различие. Ещё одним дополнительным обстоятельством, способствующим существованию единого названия «трилистник» для обоих узлов, является то, что большинство классический табуляций в связи с экономией места не различают зеркальные узлы друг от друга.
Будучи простейшими узлами сразу по ряду показателей, трилистники нередко выступают как классические примеры или контр-примеры в различных теоретико-узловых рассуждениях, наряду с другим «несложным» узлом восьмёркой[3]. Выдвигаемые гипотезы или обширные концепции нередко в первую очередь оказываются проверены и изучены именно в случае трилистников, если это представляется возможным в рамках предположений[4]. Во многом в связи с этим трилистники – одни из наиболее подробно исследованных узлов.
Трилистники часто возникают в химии и молекулярной биологии как форма заузленности молекул (в таких случаях они иногда называются молекулярными или органическими трилистниками), являясь в этом виде классическими представителями пересечения абстрактной топологии с естественными науками[5][6].
Кроме того, различные изображения трилистников встречаются на многих артефактах разных культур и эпох – трилистники нередко использовались в качестве мистического или религиозного символа (в этом смысле чаще встречаются более локальные и специальные понятия вроде трикветр или валькнут), а также в искусстве, например, как составная часть росписей, узоров или мозаик.
В современном мире символ трилистника не менее популярен и различные стилизованные изображения трилистников нередко можно встретить на эмблемах и логотипах, в качестве декоративных элементов или в произведениях искусства.
Наряду с кольцами Борромео, зацеплением Хопфа, тривиальным узлом и некоторыми другими понятиями как классической теории узлов, так и топологии в целом, трилистники являются ключевым объектом в изложении и практике спорного[7] психоаналитического исследования философов Жака Лакана и Жана-Мишеля Вапперо[8].
Определение
[править | править код]-
Левый трилистник
-
Правый трилистник
Когда речь заходит о трилистниках, в математической литературе обычно даётся одновременно некорректное и остенсивное определение, а именно, приводится изображение одного (правого или левого) трилистника и подпись вида «на этом рисунке изображён узел трилистник»[9][10][2][11][12]. Чаще всего это связано с предполагаемым уровнем знаний читателя – в работах для начинающих излагаемые ниже тонкие детали предполагаются несущественными, а в изданиях для профессионалов – хорошо известными. Кроме того, существует и другая неоднозначность – на рисунке справа (как и везде далее) трилистники называются левым и правым в соответствии с обозначениями книги Кунио Мурасуги «Knot Theory & Its Applications» (Murasugi, 1996), однако в этом случае нет общего устоявшегося соглашения о нотации. Так, например, в другом классическом учебнике «Knot theory» Чарльза Ливингстона (Livingston, 1996) используются противоположные обозначения[13][14][15].
Конечно, в случае определения с помощью рисунка, всегда подразумевается, что соответствующим трилистником называется любой геометрический узел, объемлюще-изотопный геометрическому узлу, образ которого изображён на рисунке, а также соответствующий объемлюще-изотопический класс.
Нередко слова «левый» и «правый» в принципе оказываются опущены в изложении. В таком случае обычно один из двух трилистников называется «трилистником», а другой — его «зеркальным образом». Действительно, левый и правый трилистники являются зеркальными образами друг друга, то есть диаграмма, полученная одновременным переключением всех перекрёстков на произвольной диаграмме правого трилистника, оказывается диаграммой левого трилистника и наоборот (определение зеркального образа корректно, так как «зеркальные отражения» движений Рейдемейстера являются движениями Рейдемейстера).
Кроме того, нетривиальным результатом является и то, что подобная терминология в принципе осмыслена, а левый и правый трилистники — действительно различные нетривиальные узлы, то есть являются несовпадающими объемлюще-изотопическими классами геометрических узлов. Впервые этот результат получил[16] Макс Ден в 1914 году, исследуя введенную им в этой же работе группу узла вместе с так называемой «периферической системой» в виде меридиана и параллели, однако со временем появились и другие, менее трудоёмкие способы различить два трилистника, к примеру раскраски узлов или полиномиальные инварианты[17].
Хотя визуальное определение и является наиболее распространённым, существует ряд и более аккуратных эквивалентных определений, пусть и задействующих некоторые дополнительные концепции.
Косы
[править | править код]-
Двуниточная коса
Правым трилистником называется любой геометрический узел, объемлюще изотопный замыканию Александера косы с двумя нитями, а также соответствующий объемлюще-изотопический класс.
Торические узлы
[править | править код]-
Правый трилистник, вложенный в тор
Правым трилистником называется торический узел . Иными словами, правым трилистником называется любой геометрический узел, объемлюще изотопный простой замкнутой кривой в , заданной параметрически как
и лежащей на торе
а также соответствующий объемлюще-изотопический класс.
Рациональные тэнглы
[править | править код]Правым трилистником называется любой геометрический узел, объемлюще изотопный числителю рационального тэнгла с дробью , а также соответствующий объемлюще-изотопический класс.
В каждом из приведённых выше случаев левый трилистник можно определить либо по аналогии, заменяя соответствующие знаки на противоположные, либо как зеркальный образ правого трилистника по определению.
Кроме того, заметим, что иногда термин «трилистник» всё таки имеет место быть без дополнительных уточнений. Дело в том, что всё изложенное выше (и далее) подразумевает работу с определением узла, основанном на понятии объемлющей изотопии. Существует также и эквивалентное этому определение, где под узлом также понимается некоторый класс эквивалентности геометрических узлов, но два геометрических узла теперь называются эквивалентными, если существует соответствующий гомеоморфизм пар (образ узла, трёхмерная сфера), переводящий образ одного геометрического узла в образ другого и сохраняющий ориентацию трёхмерной сферы[2]. Однако в некоторых работах условие сохранения ориентации опускается, в связи с чем, оказывается допустимым гомеоморфизм, реализующий зеркальное отражение. Иными словами, в определении, не учитывающем сохранение ориентации, узел и его зеркальный образ являются одним и тем же узлом по определению. В частности, в таком определении левый и правый трилистники ничем не различаются и корректно использование одного слова для указания на любой из них. Но в связи с тем, что такое определение хоть и удобно для пользования в свете определенных задач и вопросов, но утрачивает достаточно широкий круг деталей, всё изложение настоящей статьи производится в объемлюще-изотопическом смысле.
Свойства
[править | править код]Комбинаторные
[править | править код]
- Правый и левый трилистники – единственные узлы, допускающие диаграмму с тремя перекрёстками, причем в обоих случаях эта диаграмма минимальна. Иначе говоря, трилистники – единственные узлы с числом перекрёстков равным .
- Правый и левый трилистники являются рациональными (или двумостовыми) узлами с дробями и соответственно.
- Оба трилистника являются альтернированными узлами.
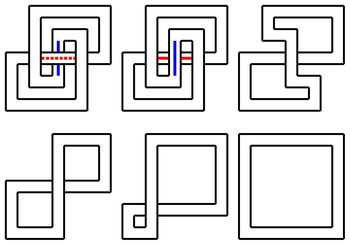
- Оба трилистника имеют число развязывания, равное .

- Оба трилистника имеют число отрезков, равное , причём это наименьшее значение, которое принимает число отрезков на нетривиальных узлах. Кроме того, трилистники – единственные узлы с таким числом отрезков[18].
- Оба трилистника имеют индекс косы равный , так как правый трилистник можно определить как замыкание Александера косы с двумя нитями, а левый – как замыкание Александера косы с двумя нитями, а индекс косы нетривиального узла всегда больше или равен .

- Оба трилистника являются -раскрашиваемыми.
- Любой узел за конечное количество пасс-мувов можно преобразовать либо в тривиальный узел, либо в один из трилистников, причем трилистники тоже можно преобразовать друг в друга за конечное число пасс-мувов. Однако тривиальный узел нельзя преобразовать ни в левый, ни в правый трилистник за конечное число пасс-мувов. Более точно, гордиев граф преобразования пасс-мув имеет две компоненты связности, в одной содержится тривиальный узел, а в другой – оба трилистника. Если вершина гордиева графа пасс-мува, соответствующая некоторому данному узлу, в лежит в компоненте связности тривиального узла, то инвариант Арфа этого узла равен , а если в компоненте трилистников, то . Следовательно, оба трилистника имеют инвариант Арфа, равный . Это замечание, в частности, можно рассматривать как эквивалентное определение инварианта Арфа[19].
- Левый и правый трилистники не допускают зеркального сглаживания или, иначе говоря, не являются зеркально косметически эквивалентными. Это означает, что ни одна диаграмма правого трилистника не имеет такого перекрёстка, разрешение (сглаживание) которого бы дало диаграмму левого трилистника (и наоборот). Иными словами, в гордиевом графе -мува нет ребра, соединяющего трилистники[20].

- Если – узел, являющийся связной суммой узлов, каждый из которых либо левый, либо правый трилистник, то его число развязывания и -число развязывания равны в точности исходя из гомологической оценки Хоста-Наканиши-Таниямы. В частности, из этого факта следует, что гордиевы графы переключения перекрёстков и -мува имеют бесконечный диаметр[21].
Топологические
[править | править код]
- Дополнения трилистников гомеоморфны (так как отражение является гомеоморфизмом). Оба трилистника имеют группу узла, допускающую копредставление . Другое копредставление этой же группы говорит об изоморфности этой группы группе кос с тремя нитями. Эта связь объясняется гомотопической эквивалентностью конфигурационного пространства трёх различных неупорядоченных точек на плоскости и внутренности дополнения трилистников.
- -листное разветвлённое накрытие , разветвлённое в правом трилистнике, гомеоморфно -листному разветвлённому накрытию , разветвлённому в левом трилистнике, и обычно обозначается через . Эти пространства исследованы достаточно подробно, в частности, известны их фундаментальные группы и группы гомологий[22]. Так, при учёте обозначения справедливо следующее,
- Некоторые из этих разветвлённых накрытий обладают необычными свойствами или являются особенными примечательными многообразиями. Так, например,
- двулистное накрытие гомеоморфно линзовому пространству [23],
- фундаментальная группа трёхлистного накрытия изоморфна группе кватернионов[24],
- фундаментальная группа четырёхлистного накрытия изоморфна бинарной группе тетраэдра[25],
- пятилистное накрытие гомеоморфно гомологической сфере Пуанкаре, а его фундаментальная группа изоморфна бинарной группе икосаэдра[25],
- -листные накрытия являются попарно негомеоморфными гомологическими сферами[26],
- -листное накрытие гомеоморфно многообразию Брискорна [22].
- Оба трилистника имеют род, равный .
- Оба трилистника имеют туннельное число, равное [27].
- Оба трилистника не являются ни срезанными (например, потому что их сигнатуры не равны нулю), ни топологически срезанными узлами. Оба имеют срезанный род, равный , и топологический срезанный род, равный [28].
- Оба трилистника являются расслоенными узлами[29].
- Правый трилистник используется для построения многообразия Черна. Говоря более подробно, правый трилистник с оснащением задаёт приклеивание четырёхмерной -ручки к четырёхмерному шару. Получающееся после приклеивания -многообразие обычно называют -следом правого трилистника. Трёхмерное многообразие, являющееся границей -следа правого трилистника, является гомологической сферой, а значит, по результату Михаэля Фридмана, ограничивает топологически стягиваемое -многообразие . Тогда многообразие Черна определяется как склейка по границе -следа правого трилистника и многообразия [30].
- Луис Мозер получил полное описание всех возможных пространств, которые получаются из трёхмерной сферы хирургией Дена с коэффициентом по торическому узлу , то есть, в частности и по трилистникам[31].
Геометрические
[править | править код]- Оба трилистника имеют дуговой индекс, равный , и допускают -страничное представление[28][32].
- Правый и левый трилистники являются торическими узлами и соответственно.
Алгебраические
[править | править код]- Оба трилистника являются простыми узлами (например, так как трилистники имеют род , а род аддитивен относительно связного суммирования).
- Правый трилистник имеет сигнатуру, равную , а левый – равную . Оба трилистника имеют детерминант, равный [33][34].
| Многочлен Александера | Многочлен Джонса | Многочлен Кауфмана | HOMFLY-PT | |
|---|---|---|---|---|
| Правый трилистник | ||||
| Левый трилистник |
Симметрии
[править | править код]Оба трилистника являются двусторонними узлами, иначе говоря:
- Оба трилистника являются обратимыми узлами, то есть два геометрических узла, представляющих объемлюще-изотопический класс правого трилистника, с введёнными на них противоположным образом ориентациями являются объемлюще-изотопными с сохранением ориентации, то есть в процессе объемлющей изотопии один ориентированный геометрический узел переходит в другой таким образом, что в итоге совпадут не только их образы, но и ориентации (аналогично для левого). Кроме того, оба трилистника являются строго обратимыми.
- Оба трилистника являются хиральными узлами, то есть правый трилистник и его зеркальный образ (левый трилистник) являются несовпадающими объемлюще-изотопическими классами геометрических узлов (аналогично для левого).
Кроме того, оба трилистника являются периодическими с периодом [35].
Трилистники в других областях знаний
[править | править код]Молекулярная биология
[править | править код]
С восьмидесятых годов двадцатого века в молекулярной биологии активно исследуются механически соединённые молекулярные структуры, аналогичные обыкновенным макроскопическим узлам – молекулярные узлы. Трилистники, как наиболее геометрически простые узлы, нередко оказываются выделены как непосредственно природно, так и в процессе исследований. Так, например, трилистники являются самой распространённой формой заузливания белков в естественной природе[36], а первым искусственно синтезированным молекулярным узлом был левый трилистник, полученный Жан-Пьером Соважем и коллегами в 1989 году[37].
Зоология
[править | править код]
Глубоководные бесчелюстные существа миксины обладают способностью завязывать собственное длинное и гибкое тело в узел трилистник (чаще всего левый), причем эта способность носит вполне утилитарный характер. Так, например, если миксине грозит опасность, она завязывает собственный хвост узлом, выделяет ядовитый слизистый секрет и начинает продвигать узел далее по телу, нанося секрет по всей его длине и обволакивая себя ядовитым коконом из слизи. Позже аналогичным образом миксина очищает себя от слизистого покрытия, сдвигая узел из собственного тела в обратную сторону[1].
Психоанализ Лакана
[править | править код]
В психоаналитической теории Лакана идея «узла-трилистника» играет ключевую роль в описании структуры паранойи. Впервые Лакан упоминает узел трилистник (здесь и далее без уточнения о том, правый или левый), на семинаре RSI (22 семинар) в 1974 году, где сообщает, что этот узел тесно связан с зацеплением Борромео – трилистник получается из зацепления Борромео путем переклеивания нитей в трёх перекрёстках – между Воображаемым и Реальным, между Символическим и Воображаемым и между Реальным и Символическим. Лакан подчеркивает, что после этого преобразования утрачивается наличие трёх компонент, «регистры больше не могут быть дифференцированы», но «форма» зацепления Борромео остаётся, и всё ещё можно определить «местоположение четырёх отверстий, в которых находятся различные типы наслаждения». Такое преобразование он называет «непрерывностью» или «интерференцией между регистрами». Связь трилистника с паранойей объясняется уже в 23 семинаре в 1975 году: «если субъект связывает в тройку воображаемое, символическое и реальное, то он поддерживается только своей непрерывностью, эти три составляют одну и ту же последовательность. И это то, из чего состоит паранойяльный психоз»[38]. Эту идею развивает Жан-Мишель Вапперо в своей работе «Узел», где говорит об узле трилистнике как о паранойяльном бреде[39].
Не смотря на широкую популярность и культовый статус теоретико-узлового метода Лакана среди его учеников и последователей, научная общественность скептически относится к подобного рода исследованиям, ставя под сомнение не только уместность пространных аналогий между топологическими объектами и психическими состояниями, но и в принципе осмысленность тех или иных терминов, предложений или даже текстов Лакана. Так, например, Жан Брикмон и Алан Сокал в своей работе «Интеллектуальные уловки: критика современной философии постмодерна» резюмируют математическую составляющую работ Лакана следующим образом: «…его аналогии между психоанализом и математикой невообразимо произвольны, и он не даёт им абсолютно никакого концептуального или эмпирического оправдания. В конечном счёте, мы думаем, что вышеприведённые тексты служат красноречивым свидетельством выставленной напоказ поверхностной эрудиции и манипулирования фразами, лишёнными смысла...»[7].
Символические изображения трилистников
[править | править код]Искусство, религия и культура
[править | править код]-
Текстильный дизайн с левыми трилистниками в обрамлении переплетающегося сотового узора с жемчугами, изготовлен в Мюлузе, Эльзас, 1840 год, экспонат Метрополитен-музея
-
Скульптура «VALKYRE» в виде правого трилистника и её автор, американский скульптор T Barny
-
Орнаментальный левый трилистник на странице Паренесиса Ефрема Сирина, XI век, Библиотека РАН
-
Левый трилистник как элемент Уппландской рунической надписи номер 937, Университетский парк, XI век, Уппсала, Швеция
-
Левый и правый трилистники как части двукомпонентых зацеплений с тривиальным узлом, вырезанные на камне проповедником Георгом Густавссоном, XX век, Швеция
-
Левый трилистник на капители Маульброннского монастыря, 1147 год, Германия
-
Двукомпонентное зацепление из левого трилистника и тривиального узла на ноктурлабиуме
-
Крепление из медного сплава в виде левого трилистника, раннее средневековье, 700-1000 годы, найдено в графстве Лестершир, Великобритания
-
Золотая оправа в виде левого трилистника, раннее средневековье, 575-700 годы, найдена в графстве Норфолк, Великобритания
-
Правый трилистник в работе по дереву Эрвина Шомоджи, смешение классического японского и готического стилей
-
Связная сумма шести правых трилистников на кельтском дверном молотке за авторством дизайнера Робина Ламли
-
Левый трилистник на цветной реставрации рунического камня Харальда I Синезубого, 970-986 годы, Еллинг, Дания
-
Связная сумма четырёх левых трилистников на военном мемориале, созданном Elkana Symonds, кладбище у церкви Святого Константина, 900-1300 годы, деревня Константин, район Керриер, графство Корнуолл, Великобритания
-
Зацепление из правого трилистника и тривиального узла на алтаре церкви Святой Троицы, деревня Блитбург, графство Суффолк, Великобритания
-
Пост-средневековая медная пуговица в виде левого трилистника, 1500-1600 годы, найдена в графстве Норфолк, Великобритания
-
Медная пряжка с серебряным левым трилистником, 650-850 годы, найдена в графстве Северный Йоркшир, Великобритания
-
Медная булавочная головка с левым трилистником, 750-900 годы, найдена в графстве Ноттингемшир, Великобритания
-
Неопознанный серебряный объект с левым трилистником, 800-925 годы, найден в графстве Северный Йоркшир, Великобритания
-
Медная пряжка с левым трилистником, 800-900 годы, найдена в графстве Норфолк, Великобритания
-
Медное эмалированное подвесное крепление для чаши с левым трилистником, 650-750 годы, найдено в графстве Стаффордшир, Великобритания
-
Медная пряжка с левым трилистником, 1150-1450 годы, найдена в графстве Ист-Райдинг-оф-Йоркшир, Великобритания
-
Двукомпонентное зацепление из правого трилистника и тривиального узла на кафедре в монастыре города Крайстчёрч, графство Дорсет, Великобритания
-
Серебряное кольцо в виде правого трилистника, 600-1900 годы, найдено в графстве Сомерсет, Великобритания
Геральдика и Вексиллология
[править | править код]-
Двукомпонентное зацепление из левого трилистника и тривиального узла на гербе епископа Питера Хью Брауна, Епархия Самоа — Паго-Паго, Американское Самоа
-
Двукомпонентное зацепление из правого трилистника и тривиального узла на гербе епископа Дугласа Джона Люсии, Епархия Сиракьюса, США
-
Двукомпонентное зацепление из правого трилистника и тривиального узла на гербе епископа Альберта Уйя, Епархия Тагбиларана, Республика Филиппины
-
Левый трилистник на гербе епископа Алехандро Алкана, Архиепархия Лос-Анджелеса, США
-
Двукомпонентное зацепление из правого трилистника и тривиального узла на гербе епископа Грегори Джона Хартмайера, Епархия Саванны, США
-
Левый трилистник на гербе коммуны Дуомон,Франция
Нумизматика
[править | править код]-
Правый трилистник на аверсе именной серебряной монеты Рагналла Гутфритссона, короля Йорка, 943-944 годы
-
Левый трилистник на монете короля Норвегии Харальда III Сурового, 1047-1066 годы
Эмблемы и логотипы
[править | править код]-
Правый трилистник на логотипе национального агентства по сохранению культурного наследия Грузии
-
Призовая статуэтка европейской премии в области электронного обучения Eurelea Award в виде правого трилистника.
-
Правильно раскрашенный в три цвета левый трилистник на почтовой марке Казахстана, посвящённой 15-илетию СВМДА
-
Левый трилистник на логотипе крупнейшего португальского банка «Caixa Geral de Depósitos»
-
Правый трилистник на логотипе испанского политического формирования Utiel Siglo XXI
-
Левый трилистник в форме валькнута на почтовой марке США, посвященной 50-летию службе национальных парков США
-
Правый трилистник на логотипе телекомпании Asia Television Limited, Гонконг
-
Двукомпонентное зацепление из правого трилистника и тривиального узла на логотипе Исследовательского и Антропологического Центра Призваний, основанного кардиналом Марком Уэлле, Сен-Клу, Франция
-
Правый трилистник в форме валькнута на логотипе Шведского целлюлозного предприятия
-
Правильно раскрашенный в три цвета левый трилистник в форме валькнута на логотипе бангладешского телеканала ATN Bangla
-
Левый трилистник в форме валькнута на логотипе группы компаний HENNLICH
-
Двукомпонентное зацепление из правого трилистника и тривиального узла на эмблеме Оссианского общества Университета Глазго
-
Правый трилистник, правильно раскрашенный в три цвета, на эмблеме конференции Викимедиа по многоязычию Celtic Knot Conference 2020
-
Правый трилистник на логотипе группы нидерладских банков Триодос Банк
Примечания
[править | править код]- ↑ 1 2 Сосинский А. Б., 2005.
- ↑ 1 2 3 Rolfsen, 2003.
- ↑ Rolfsen, 2003, Главы «Cyclic coverings of branched over the trefoil» и «Fibering the complement of a trefoil».
- ↑ Gompf, 1986.
- ↑ Ponnuswamy, Cougnon, Clough, Pantoş, Sanders, 2012.
- ↑ Rapenne, Dietrich-Buchecker, Sauvage, 1996.
- ↑ 1 2 Брикмон, Сокал, 2002.
- ↑ Вапперо Ж.-М., 2022.
- ↑ Burde, Zieschang, 2013.
- ↑ Adams, 2004.
- ↑ Livingston, 1996.
- ↑ Kawauchi, 1996.
- ↑ Burde, Zieschang, 2013, Есть термины «левый» и «правый» трилистник, обозначены противоположно варианту Мурасуги.
- ↑ Adams, 2004, Нет терминов «левый» и «правый» трилистник, левый назван «трилистником» правый – его «отражением».
- ↑ Kawauchi, 1996, Введены термины «левый» и «правый» трилистники, однако употребляются единожды, а во всех остальных случаях «трилистником» и его «отражением» называются попеременно оба узла.
- ↑ Dehn, 1914.
- ↑ Burde, Zieschang, 2013, p. 322.
- ↑ Jin, 1997.
- ↑ Kauffman, 1987, p. 74-78.
- ↑ Livingston, 2020.
- ↑ Hoste, Nakanishi, Taniyama, 1990.
- ↑ 1 2 Mulazzani, Vesnin, 2001.
- ↑ Rolfsen, 2003, p. 304.
- ↑ Rolfsen, 2003, p. 305.
- ↑ 1 2 Rolfsen, 2003, p. 306.
- ↑ Rolfsen, 2003, p. 308.
- ↑ Morimoto, 2016.
- ↑ 1 2 KnotInfo, 2004.
- ↑ Rolfsen, 2003, Глава «Fibering the complement of a trefoil», p. 327.
- ↑ Freedman, 1982.
- ↑ Sullivan, 2013.
- ↑ Dynnikov, 2000.
- ↑ Rolfsen, 2003, p. 220.
- ↑ Burde, Zieschang, 2013, p. 243.
- ↑ Livingston, 1996, p. 156.
- ↑ Jamroz, Niemyska, Rawdon, Stasiak, Millett, Sułkowski, Sulkowska, 2015.
- ↑ Albrecht-Gary, Meyer, Dietrich-Buchecker, Sauvage, Guilhem, Pascard, 2010.
- ↑ Godoy, 2004.
- ↑ Вапперо Ж.-М., 2022, p. 289.
Литература
[править | править код]Математические материалы
- Сосинский А. Б. Хронология одной математической теории. — МЦНМО, 2005. — 112 с. — ISBN 5-94057-220-0.
- Adams C. C. The Knot Book. An Elementary Introduction to the Mathematical Theory of Knots (англ.). — New York: American Mathematical Society, 2004. — 307 p. — ISBN 978-0821836781.
- Burde G., Zieschang H., Heusener M. Knots (англ.). — Walter de gruyter, 2013. — Vol. 5. — 417 p. — ISBN 978-3110270747.
- Dehn M. Die beiden kleeblattschlingen (нем.) // Mathematische Annalen. — 1914. — Bd. 75, Nr. 3. — S. 402-413. — doi:10.1007/BF01563732.
- Freedman M. H. The topology of four-dimensional manifolds (англ.) // Journal of Differential Geometry. — 1982. — Vol. 17, no. 3. — P. 357-453. — doi:10.4310/jdg/1214437136.
- Gompf R. E. Smooth concordance of topologically slice knots (англ.) // Topology. — 1986. — Vol. 25, no. 3. — P. 353-373. — doi:10.1016/0040-9383(86)90049-2.
- Hoste J., Nakanishi Y., Taniyama K. Unknotting operations involving trivial tangles (англ.) // Osaka Journal of Mathematics. — 1990. — Vol. 27, no. 3. — P. 555-566. — doi:10.18910/10958.
- Jin G. T. Polygon indices and superbridge indices of torus knots and links (англ.) // Journal of Knot Theory and its Ramifications. — 1997. — Vol. 6, iss. 2. — P. 281—289. — doi:10.1142/S0218216597000170.
- Kauffman L. H. On knots (англ.). — Princeton University Press, 1987. — Vol. 115. — 423 p. — (Annals of Mathematics Studies). — ISBN 0-691-08435-1.
- Kawauchi A. Survey on knot theory (англ.). — Birkhäuser Basel, 1996. — 423 p. — ISBN 978-3-0348-9227-8. — doi:10.1007/978-3-0348-9227-8.
- Livingston C. Knot Theory (англ.). — The Mathematical Association of America, 1996. — Vol. 24. — 258 p. — (The Carus Mathematical Monographs). — ISBN 978-0883850275.
- Livingston C. Chiral smoothings of knots (англ.) // Proceedings of the Edinburgh Mathematical Society. — 2020. — Vol. 63, iss. 4. — P. 1048-1061. — doi:10.1017/S0013091520000322.
- Morimoto K. Tunnel numbers of knots (англ.) // Knot Theory and Its Applications. — 2016. — Vol. 670. — P. 327.
- Mulazzani M., Vesnin A. The many faces of cyclic branched coverings of -bridge knots and links (англ.) // arXiv preprint. — 2001.
- Murasugi K., Kurpita B. Knot theory and its applications (англ.). — Boston: Birkhäuser, 1996. — 341 p. — ISBN 978-0-8176-4719-3.
- Rolfsen D. Knots and links (англ.). — American Mathematical Society, 2003. — Vol. 346. — 439 p. — ISBN 978-0821834367.
- Sullivan M. Trefoil surgery (англ.) // Preprint. — 2013.
Прочее
- Вапперо Ж.-М. Узел. Теория узла по стопам Ж. Лакана. — Логос, 2022. — 390 с. — ISBN 987-5-94244-084-8.
- Брикмон Ж., Сокал А. Интеллектуальные уловки. Критика современной философии постмодерна / Пер. с англ. Костиковой А. и Кралечкина Д., предисловие Капицы С. П.. — Москва: Дом интеллектуальной книги, 2002. — 248 с.
- Albrecht-Gary A. M., Meyer M., Dietrich-Buchecker C. O., Sauvage J. P., Guilhem J., Pascard C. Dicopper (I) trefoil knots: Demetallation kinetic studies and molecular structures (англ.) // Recueil des Travaux Chimiques des Pays-Bas : journal. — 2010. — 2 September (vol. 112, no. 6). — P. 427-428. — doi:10.1002/recl.19931120622.
- Godoy C. El nudo trébol en la enseñanza de J. Lacan (исп.) // XI Jornadas de Investigación. – Facultad de Psicología-Universidad de Buenos Aires : journal. — 2004.
- Jamroz M., Niemyska W., Rawdon E., Stasiak A., Millett K. C., Sułkowski P., Sulkowska J. I. KnotProt: a database of proteins with knots and slipknots (англ.) // Nucleic Acids Research : journal. — 2015. — 28 January (vol. 43). — P. D306–D314. — doi:10.1093/nar/gku1059.
- Ponnuswamy, N., Cougnon, F. B., Clough, J. M., Pantoş, G. D., Sanders, J. K. Discovery of an organic trefoil knot (англ.) // Science. — 2012. — Vol. 338, no. 6108. — P. 783-785. — doi:10.1126/science.1227032.
- Rapenne G., Dietrich-Buchecker C., Sauvage J. P. Resolution of a molecular trefoil knot (англ.) // Journal of the American Chemical Society. — 1996. — Vol. 118, no. 44. — P. 10932-10933. — doi:10.1021/ja961898o.
Ссылки
[править | править код]- Livingston C., Moore A. H. KnotInfo: Table of Knots (англ.). Indiana University Bloomington (2004). Дата обращения: 18 февраля 2023.
- Dynnikov I. Trefoil Knot (англ.). Electronic Geometry Models (2000). Дата обращения: 18 февраля 2023.