Сферическая система координат: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
Fascinum (обсуждение | вклад) →Дифференциальные характеристики: Неправильный знак |
|||
| (не показано 112 промежуточных версий 46 участников) | |||
| Строка 1: | Строка 1: | ||
'''Сфери́ческая систе́ма координа́т''' — [[Трёхмерное пространство|трёхмерная]] [[система координат]], в которой каждая точка [[Пространство в физике|пространства]] определяется тремя числами <math>(r,\;\theta,\;\varphi)</math>, где <math>r</math> — расстояние до [[Начало координат|начала координат]] (радиальное расстояние), а <math>\theta</math> и <math>\varphi</math> — зенитный и азимутальный [[Угол|углы]] соответственно. |
|||
[[Файл:Spherical with grid.svg|thumb|right|Точка <math>P</math> имеет три декартовых и три сферических координаты]] |
|||
Понятия ''[[Зенит (астрономия)|зенит]]'' и ''[[Азимут (астрономия)|азимут]]'' широко используются в [[Астрономия|астрономии]]. '''[[Зенит]]''' — направление вертикального подъёма над произвольно выбранной точкой (точкой наблюдения), принадлежащей '''[[Фундаментальная плоскость|фундаментальной плоскости]]'''. В качестве фундаментальной плоскости в астрономии может быть выбрана плоскость, в которой лежит экватор, или плоскость, в которой лежит горизонт, или плоскость эклиптики и т. д., что порождает разные системы небесных координат. '''[[Азимут]]''' — угол между произвольно выбранным лучом фундаментальной плоскости с началом в точке наблюдения и другим лучом этой плоскости, имеющим общее начало с первым. |
|||
Сферическую систему координат удобно определять, соотносясь с декартовой прямоугольной системой координат (см. рисунок): |
|||
[[Файл:Spherical with grid.svg|thumb|300px|Рис. 1.Точка имеет три декартовых и три сферических координаты]] |
|||
'''Сферическими координатами''' называют систему координат для отображения геометрических свойств фигуры в трёх измерениях посредством задания трёх координат <math>(r,\;\theta,\;\varphi)</math>, где <math>r</math> — расстояние до [[Начало координат|начала координат]], а <math>\theta</math> и <math>\varphi</math> — зенитный и азимутальный углы соответственно. |
|||
Если рассматривать сферическую систему координат относительно [[Прямоугольная система координат|декартовой системы]] <math>Oxyz</math>, фундаментальной плоскостью будет плоскость <math>xy</math>, зенитным углом точки, заданной радиус-вектором <math>P</math>, будет угол между <math>P</math> и осью <math>z</math>, а азимутом — угол между проекцией <math>P</math> на плоскость <math>xy</math> и осью <math>x</math>. Это объясняет названия углов и то, что сферическая система координат может служить обобщением множества видов '''[[Система небесных координат|систем небесных координат]]'''. |
|||
== Определения == |
|||
Понятия ''[[Зенит (астрономия)|зенит]]'' и ''[[Азимут (астрономия)|азимут]]'' широко используются в [[Астрономия|астрономии]]. Вообще '''зенит''' — это направление вертикального подъёма над произвольно выбранной точкой (точкой наблюдения), принадлежащей так называемой [[Фундаментальная плоскость|'''фундаментальной плоскости''']]. В качестве фундаментальной плоскости в астрономии может быть выбрана плоскость, в которой лежит экватор, или плоскость, в которой лежит горизонт, или плоскость эклиптики и т. д., что порождает разные системы небесных координат. '''Азимут''' — угол между произвольно выбранным лучом фундаментальной плоскости с началом в точке наблюдения и другим лучом этой плоскости, имеющим общее начало с первым. |
|||
Положение точки <math>P</math> в сферической системе координат определяется тройкой <math>(r,\;\theta,\;\varphi)</math>, где |
|||
Применительно к нашему рисунку сферической системы координат, фундаментальная плоскость — это плоскость xy. Зенит — некая удалённая точка, лежащая на оси Z и видимая из начала координат. Азимут отсчитывается от оси X до проекции радиус-вектора r на плоскость xy. Это объясняет названия углов, как и то, что сферическая система координат может служить обобщением (пусть хотя бы и приближённым) множества видов [[Система небесных координат|'''систем небесных координат''']]. |
|||
== Определения == |
|||
Три координаты <math>(r,\;\theta,\;\varphi)</math> определены как: |
|||
* <math>r\geqslant 0</math> — расстояние от начала координат до заданной точки <math>P</math>. |
* <math>r\geqslant 0</math> — расстояние от начала координат до заданной точки <math>P</math>. |
||
* <math>0\leqslant\theta\leqslant 180^\circ</math> — угол между осью <math> |
* <math>0^\circ\leqslant\theta\leqslant 180^\circ</math> — угол между осью <math>z</math> и отрезком, соединяющим начало координат и точку <math>P</math>. |
||
* <math>0\leqslant\varphi< 360^\circ</math> — угол между осью <math> |
* <math>0^\circ\leqslant\varphi< 360^\circ</math> — угол между осью <math>x</math> и проекцией отрезка, соединяющего начало координат с точкой <math>P</math>, на плоскость <math>xy</math> (см. рис. 1). |
||
Угол <math>\theta</math> называется '''зенитным''', или '''полярным''', или '''нормальным''', а также он может быть назван английским словом '''colatitude''', а угол <math>\varphi</math> — '''азимутальным'''. |
|||
Углы <math>\theta</math> и <math>\varphi</math> не имеют значения при <math>r=0</math>, а <math>\varphi</math> не имеет значения при <math>\sin(\theta)=0</math> (то есть при <math>\theta=0</math> или <math>\theta=180^\circ</math>). |
|||
Угол <math>\theta</math> называется '''зенитным''', или '''полярным''', также он может называться '''наклонением''', или '''коширотой''', а угол <math>\varphi</math> — '''азимутальным'''. Углы <math>\theta</math> и <math>\varphi</math> не определены при <math>r=0</math>, также не определён угол <math>\varphi</math> при <math>\sin(\theta)=0</math> (то есть при <math>\theta=0</math> или <math>\theta=180^\circ</math>). |
|||
Зависимо или независимо от стандарта ([[ISO 31-11]]), существует и такое соглашение или [[конвенция]] ({{lang-en|convention}}), когда вместо зенитного угла <math>\theta</math>, используется угол между проекцией радиус-вектора точки r на плоскость xy и самим радиус-вектором r, равный <math>90^\circ</math> — <math>\theta</math>. Он называется '''углом подъёма''' и может быть обозначен той же буквой <math>\theta</math>. |
|||
В этом случае он будет изменяться в пределах <math>-90^\circ\leqslant\theta\leqslant 90^\circ</math>. |
|||
Такое соглашение установлено в стандарте ([[ISO 31-11]]). Кроме того может использоваться соглашение, когда вместо зенитного угла <math>\theta</math>, используется угол между радиус-вектором точки <math>P</math> и плоскостью <math>xy</math>, равный <math>90^\circ - \theta</math>. Он называется '''широтой''' и может быть обозначен той же буквой <math>\theta</math>. Широта может изменяться в пределах <math>-90^\circ\leqslant\theta\leqslant 90^\circ</math>. При этом соглашении углы <math>\theta</math> и <math>\varphi</math> не имеют значения при <math>r=0</math>, так же как и в первом случае, а <math>\varphi</math> не имеет значения при <math>\cos(\theta)=0</math> (то есть при <math>\theta=-90^\circ</math> или <math>\theta=90^\circ</math>). |
|||
== Переход к другим системам координат == |
== Переход к другим системам координат == |
||
* [[Прямоугольная система координат|Декартова система координат]] |
|||
=== [[Прямоугольная система координат|Декартова система координат]] === |
|||
** Если заданы сферические координаты точки, то переход к декартовым осуществляется по формулам: |
|||
Если заданы сферические координаты точки <math>(r,\;\theta,\;\varphi)</math>, то переход к декартовым осуществляется по формулам: |
|||
**: <math>\begin{cases} |
|||
: <math>\begin{cases} |
|||
x=r\sin\theta\cos\varphi, \\ |
x=r\sin\theta\cos\varphi, \\ |
||
y=r\sin\theta\sin\varphi, \\ |
y=r\sin\theta\sin\varphi, \\ |
||
z=r\cos\theta. |
z=r\cos\theta. |
||
\end{cases}</math> |
\end{cases}</math> |
||
** Обратно, от декартовых к сферическим: |
|||
Обратно, от декартовых к сферическим: |
|||
**: <math>\begin{cases} |
|||
: <math>\begin{cases} |
|||
r=\sqrt{x^2+y^2+z^2}, \\ |
r=\sqrt{x^2+y^2+z^2}, \\ |
||
\theta=\arccos |
\theta=\arccos\dfrac{z}{\sqrt{x^2+y^2+z^2}}=\mathrm{arctg}\dfrac{\sqrt{x^2+y^2}}{z}, \\ |
||
\varphi=\mathrm{arctg} |
\varphi=\mathrm{arctg}\dfrac{y}{x}. |
||
\end{cases}</math> |
\end{cases}</math> |
||
*** (здесь, конечно, требуется определенное естественное уточнение для значений <math>\varphi</math> вне первого октанта; то же для всех формул с [[арктангенс]]ом здесь и ниже; впрочем, замена на соответствующую формулу с арккосинусом снимает этот вопрос в отношении координаты <math>\theta</math>). |
|||
[[Якобиан]] преобразования к сферическим координатам равен |
|||
**: <math>J=r^2\sin\theta.\ </math> |
|||
: <math>\begin{alignat}{2} |
|||
* [[Цилиндрическая система координат]] |
|||
J & =\frac{\partial(x,y,z)}{\partial (r,\theta,\varphi)}=\begin{vmatrix} |
|||
** Если заданы сферические координаты точки, то переход к цилиндрическим осуществляется по формулам: |
|||
\sin \theta \cos \varphi & r \cos \theta \cos \varphi & -r\sin\theta\sin\varphi \\ |
|||
**: <math>\begin{cases} |
|||
\sin \theta \sin \varphi & r \cos \theta \sin \varphi & r \sin \theta \cos \varphi \\ |
|||
\cos \theta & - r\sin\theta & 0 |
|||
\end{vmatrix} |
|||
= \\ & =\cos \theta (r^2 \cos \varphi^2 \cos \theta \sin \theta + r^2\sin^2\varphi \cos\theta\sin\theta) + r\sin\theta(r\sin^2\theta\cos^2\varphi + r\sin^2\theta\sin^2\varphi) = \\ & = r^2 \cos^2\theta \sin \theta + r^2 \sin^2 \theta \sin\theta =\\ &= |
|||
r^2\sin\theta. |
|||
\end{alignat} </math> |
|||
Таким образом, элемент объёма при переходе от декартовых к сферическим координатам будет выглядеть следующим образом: |
|||
: <math> |
|||
\mathrm{d}V = \mathrm{d}x\, \mathrm{d}y\, \mathrm{d}z = J(r,\theta,\varphi) \,\mathrm{d}r\,\mathrm{d}\theta\,\mathrm{d}\varphi = r^2 \sin \theta \, \,\mathrm{d}r\,\mathrm{d}\theta\,\mathrm{d}\varphi |
|||
</math> |
|||
=== [[Цилиндрическая система координат]] === |
|||
Если заданы сферические координаты точки, то переход к цилиндрическим осуществляется по формулам: |
|||
: <math>\begin{cases} |
|||
\rho=r\sin\theta, \\ |
\rho=r\sin\theta, \\ |
||
\varphi=\varphi, \\ |
\varphi=\varphi, \\ |
||
z=r\cos\theta. |
z=r\cos\theta. |
||
\end{cases}</math> |
\end{cases}</math> |
||
Обратно от цилиндрических к сферическим: |
|||
: <math>\begin{cases} |
|||
r=\sqrt{\rho^2+z^2}, \\ |
r=\sqrt{\rho^2+z^2}, \\ |
||
\theta=\mathrm{arctg} |
\theta=\mathrm{arctg}\dfrac{\rho}{z}, \\ |
||
\varphi=\varphi. |
\varphi=\varphi. |
||
\end{cases}</math> |
\end{cases}</math> |
||
[[Якобиан]] преобразования от сферических к цилиндрическим <math>J=r </math>. |
|||
**: <math>J=r.\ </math> |
|||
== Дифференциальные характеристики == |
== Дифференциальные характеристики == |
||
| Строка 63: | Строка 75: | ||
: <math> |
: <math> |
||
\boldsymbol{\hat r} |
\boldsymbol{\hat r} |
||
=\sin \theta \cos \ |
=\sin \theta \cos \varphi \boldsymbol{\hat{\imath}} + |
||
\sin \theta \sin \ |
\sin \theta \sin \varphi \boldsymbol{\hat{\jmath}} + |
||
\cos \theta \boldsymbol{\hat{k}} |
\cos \theta \boldsymbol{\hat{k}} |
||
</math> |
</math> |
||
: <math> \boldsymbol{\hat\theta } |
: <math> \boldsymbol{\hat\theta } |
||
=\cos \theta \cos \ |
=\cos \theta \cos \varphi \boldsymbol{\hat{\imath}} + |
||
\cos \theta \sin \ |
\cos \theta \sin \varphi \boldsymbol{\hat{\jmath}} |
||
-\sin \theta \boldsymbol{\hat{k}} |
-\sin \theta \boldsymbol{\hat{k}} |
||
</math> |
</math> |
||
: <math> |
: <math> |
||
\boldsymbol{\hat \varphi} |
\boldsymbol{\hat \varphi} |
||
=\sin \ |
=-\sin \varphi \boldsymbol{\hat{\imath}} + \cos \varphi \boldsymbol{\hat{\jmath}} |
||
</math> |
</math> |
||
ортогональные единичные векторы сферических координат в направлении увеличения <math>r,\theta,\varphi</math>, соответственно, |
ортогональные [[Единичный вектор|единичные векторы]] сферических координат в направлении увеличения <math>r,\theta,\varphi</math>, соответственно, а <math>\boldsymbol{\hat{\imath}}, \boldsymbol{\hat{\jmath}}, \boldsymbol{\hat{k}}</math> — единичные векторы декартовых координат. Сферические координаты являются ортогональными, поэтому [[метрический тензор]] имеет в них диагональный вид: |
||
а <math>\boldsymbol{\hat{\imath}}, \boldsymbol{\hat{\jmath}}, \boldsymbol{\hat{k}}</math> — единичные векторы декартовых координат. |
|||
Сферические координаты являются ортогональными, поэтому [[метрический тензор]] имеет в них диагональный вид: |
|||
: <math>g_{ij}=\begin{pmatrix} |
: <math>g_{ij}=\begin{pmatrix} |
||
1 & 0 & 0\\ 0 & r^2 & 0\\ 0 & 0 & r^2\sin^2\theta |
1 & 0 & 0\\ 0 & r^2 & 0\\ 0 & 0 & r^2\sin^2\theta |
||
| Строка 86: | Строка 96: | ||
\end{pmatrix}</math> |
\end{pmatrix}</math> |
||
* <math>\det(g_{ij})=r^4\sin^2\theta.\ </math> |
* <math>\det(g_{ij})=r^4\sin^2\theta.\ </math> |
||
* Квадрат дифференциала длины дуги: |
* Квадрат [[Дифференциал длины дуги|дифференциала длины дуги]]: |
||
: <math>ds^2=dr^2+r^2\,d\theta^2+r^2\sin^2\theta\,d\varphi^2.</math> |
: <math>ds^2=dr^2+r^2\,d\theta^2+r^2\sin^2\theta\,d\varphi^2.</math> |
||
* [[Криволинейная система координат# |
* [[Криволинейная система координат#Коэффициенты Ламе|Коэффициенты Ламе]]: |
||
: <math>H_r=1,\quad H_\theta=r,\quad H_\varphi=r\sin\theta.</math> |
: <math>H_r=1,\quad H_\theta=r,\quad H_\varphi=r\sin\theta.</math> |
||
| Строка 96: | Строка 106: | ||
: <math>\Gamma^2_{33}=-\cos\theta\sin\theta,\quad \Gamma^3_{23}=\Gamma^3_{32}=\mathrm{ctg}\,\theta.</math> |
: <math>\Gamma^2_{33}=-\cos\theta\sin\theta,\quad \Gamma^3_{23}=\Gamma^3_{32}=\mathrm{ctg}\,\theta.</math> |
||
Остальные равны нулю. |
Остальные равны нулю. |
||
== Математическое моделирование Земли == |
|||
=== Сферическая географическая система координат === |
|||
Сферическая географическая система координат строится следующим образом<ref name="bru"/>: |
|||
* её начало помещено в центр [[Земля|Земли]]; |
|||
* полярная ось направлена по [[Вращательное движение|оси вращения]] Земли; |
|||
* координата <math>r</math> отсчитывается вдоль радиус-вектора, проведенного из центра Земли; |
|||
* полярный угол <math>\theta</math> есть ''коширота'' (дополнение географической [[Широта|широты]] до <math>90^\circ</math>); |
|||
* азимутальный угол <math>\varphi</math> совпадает с географической [[Долгота|долготой]] (восточной). |
|||
Вектор [[Магнитная индукция|магнитной индукции]] [[Магнитное поле Земли|магнитного поля Земли]] <math>\mathbf{B}</math> имеет компоненты |
|||
: <math>B_r = -B \sin I, \; B_\theta = -B \cos I \cos D, \; B_\varphi = B \cos I \sin D,</math> |
|||
где <math>I</math> — [[магнитное наклонение]]; <math>D</math> — [[магнитное склонение]]. |
|||
Компоненты вектора [[Ускорение свободного падения|ускорения свободного падения]] <math>\mathbf{g}</math> равны |
|||
: <math>g_r = -g, \; g_\theta = g_\varphi = 0.</math> |
|||
Наконец, компоненты вектора [[Суточное вращение Земли#Период и скорость вращения|угловой скорости вращения Земли]] <math>\mathbf{\Omega}</math> такие: |
|||
: <math>\Omega_r = \Omega \cos \theta, \; \Omega_\theta = -\Omega \sin \theta, \; \Omega_\varphi = 0.</math> |
|||
В сферических географических координатах оптимально решать уравнения, описывающие поведение нейтральных частиц околоземного пространства<ref name="bru"/>. |
|||
=== Сферическая геомагнитная система координат === |
|||
Сферическая геомагнитная система координат строится следующим образом<ref name="bru"/>: |
|||
* её начало помещено в центр [[Земля|Земли]]; |
|||
* полярная ось направлена по оси [[Диполь (электродинамика)#Магнитный диполь|магнитного диполя]] Земли (геомагнитной оси), проходящей через [[Магнитный полюс Земли#Геомагнитные полюса|магнитные полюса]]; |
|||
* координата <math>r</math> отсчитывается вдоль радиус-вектора, проведенного из центра Земли; |
|||
* полярный угол <math>\Theta</math> есть геомагнитная ''коширота'' (дополнение магнитной широты <math>\Phi</math> до <math>90^\circ \colon\; \Theta = \pi/2 - \Phi</math>); |
|||
* азимутальный угол <math>\Lambda</math> совпадает с геомагнитной долготой, отсчитываемой к востоку от плоскости в [[Западное полушарие|западном полушарии]], содержащей географический и геомагнитный полюсы. |
|||
Географические координаты [[Северный магнитный полюс|северного магнитного полюса]] равны |
|||
: <math>\theta_0 = 4,6^\circ, \; \varphi_0 = 43,0^\circ \; (2012).</math> |
|||
В сферической геомагнитной системе координат склонение <math>D = 0</math> и |
|||
: <math>B_r = -B \sin I, \; B_\Theta = -B \cos I, \; B_\Lambda = 0,</math> |
|||
: <math>g_r = -g, \; g_\Theta = g_\Lambda = 0.</math> |
|||
: <math>\Omega_r = \Omega (\cos \theta_0 \cos \Theta - \sin \theta_0 \sin \Theta \cos \Lambda),</math> |
|||
: <math>\Omega_\Theta = -\Omega (\cos \theta_0 \sin \Theta + \sin \theta_0 \cos \Theta \cos \Lambda),</math> |
|||
: <math>\Omega_\Lambda = \Omega \sin \theta_0 \sin \Lambda.</math> |
|||
Формулы, связывающие географические и геомагнитные сферические координаты<ref name="bru"/>: |
|||
: <math>\cos \Theta = \cos \theta_0 \cos \theta + \sin \theta_0 \sin \theta \cos (\varphi - \varphi_0),</math> |
|||
: <math>\cos \Lambda = \frac{-\sin \theta_0 \cos \theta + \cos \theta_0 \sin \theta \cos (\varphi - \varphi_0)}{\sin \Theta},</math> |
|||
: <math>\cos \theta = \cos \theta_0 \cos \Theta - \sin \theta_0 \sin \Theta \cos \Lambda,</math> |
|||
: <math>\cos (\varphi - \varphi_0) = \frac{\sin \theta_0 \cos \Theta + \cos \theta_0 \sin \Theta \cos \Lambda}{\sin \theta}.</math> |
|||
В сферических геомагнитных координатах проще, чем в сферических географических координатах, описывать влияние геомагнитного поля на заряженные частицы околоземного пространства<ref name="bru"/>. |
|||
== См. также == |
== См. также == |
||
* [[Системы небесных координат]] |
|||
* [[Полярная система координат]] |
|||
* [[Цилиндрическая система координат]] |
|||
* [[Углы Эйлера]] |
* [[Углы Эйлера]] |
||
* [[Гиперсферические координаты]] |
|||
== Примечания == |
|||
{{примечания|2|refs= |
|||
<ref name="bru">''Брюнелли Б. Е., Намгаладзе А. А.'' Физика ионосферы. М.: Наука, 1988. § 3.5, С. 172—173. {{ISBN|5-02-000716-1}}</ref> |
|||
}} |
|||
== Ссылки == |
== Ссылки == |
||
* {{MathWorld|SphericalCoordinates|Сферические координаты}} |
* {{MathWorld|SphericalCoordinates|Сферические координаты}} |
||
{{Системы координат}} |
{{Системы координат}} |
||
{{Небесная механика}} |
{{Небесная механика}} |
||
[[Категория:Системы координат]] |
[[Категория:Системы координат]] |
||
[[Категория: |
[[Категория:Сферическая геометрия|Система координат]] |
||
[[Категория:Астрометрия]] |
|||
[[Категория:Небесная механика]] |
|||
[[fi:Koordinaatisto#Pallokoordinaatisto]] |
|||
[[it:Sistema di riferimento#Il sistema sferico]] |
|||
Текущая версия от 10:29, 16 ноября 2024
Сфери́ческая систе́ма координа́т — трёхмерная система координат, в которой каждая точка пространства определяется тремя числами , где — расстояние до начала координат (радиальное расстояние), а и — зенитный и азимутальный углы соответственно.
Понятия зенит и азимут широко используются в астрономии. Зенит — направление вертикального подъёма над произвольно выбранной точкой (точкой наблюдения), принадлежащей фундаментальной плоскости. В качестве фундаментальной плоскости в астрономии может быть выбрана плоскость, в которой лежит экватор, или плоскость, в которой лежит горизонт, или плоскость эклиптики и т. д., что порождает разные системы небесных координат. Азимут — угол между произвольно выбранным лучом фундаментальной плоскости с началом в точке наблюдения и другим лучом этой плоскости, имеющим общее начало с первым.
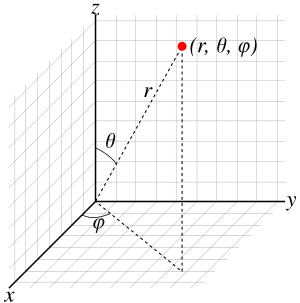
Если рассматривать сферическую систему координат относительно декартовой системы , фундаментальной плоскостью будет плоскость , зенитным углом точки, заданной радиус-вектором , будет угол между и осью , а азимутом — угол между проекцией на плоскость и осью . Это объясняет названия углов и то, что сферическая система координат может служить обобщением множества видов систем небесных координат.
Определения
[править | править код]Положение точки в сферической системе координат определяется тройкой , где
- — расстояние от начала координат до заданной точки .
- — угол между осью и отрезком, соединяющим начало координат и точку .
- — угол между осью и проекцией отрезка, соединяющего начало координат с точкой , на плоскость (см. рис. 1).
Угол называется зенитным, или полярным, также он может называться наклонением, или коширотой, а угол — азимутальным. Углы и не определены при , также не определён угол при (то есть при или ).
Такое соглашение установлено в стандарте (ISO 31-11). Кроме того может использоваться соглашение, когда вместо зенитного угла , используется угол между радиус-вектором точки и плоскостью , равный . Он называется широтой и может быть обозначен той же буквой . Широта может изменяться в пределах . При этом соглашении углы и не имеют значения при , так же как и в первом случае, а не имеет значения при (то есть при или ).
Переход к другим системам координат
[править | править код]Если заданы сферические координаты точки , то переход к декартовым осуществляется по формулам:
Обратно, от декартовых к сферическим:
Якобиан преобразования к сферическим координатам равен
Таким образом, элемент объёма при переходе от декартовых к сферическим координатам будет выглядеть следующим образом:
Если заданы сферические координаты точки, то переход к цилиндрическим осуществляется по формулам:
Обратно от цилиндрических к сферическим:
Якобиан преобразования от сферических к цилиндрическим .
Дифференциальные характеристики
[править | править код]Вектор , проведённый из точки в точку , равен
где
ортогональные единичные векторы сферических координат в направлении увеличения , соответственно, а — единичные векторы декартовых координат. Сферические координаты являются ортогональными, поэтому метрический тензор имеет в них диагональный вид:
- Квадрат дифференциала длины дуги:
Остальные равны нулю.
Математическое моделирование Земли
[править | править код]Сферическая географическая система координат
[править | править код]Сферическая географическая система координат строится следующим образом[1]:
- её начало помещено в центр Земли;
- полярная ось направлена по оси вращения Земли;
- координата отсчитывается вдоль радиус-вектора, проведенного из центра Земли;
- полярный угол есть коширота (дополнение географической широты до );
- азимутальный угол совпадает с географической долготой (восточной).
Вектор магнитной индукции магнитного поля Земли имеет компоненты
где — магнитное наклонение; — магнитное склонение.
Компоненты вектора ускорения свободного падения равны
Наконец, компоненты вектора угловой скорости вращения Земли такие:
В сферических географических координатах оптимально решать уравнения, описывающие поведение нейтральных частиц околоземного пространства[1].
Сферическая геомагнитная система координат
[править | править код]Сферическая геомагнитная система координат строится следующим образом[1]:
- её начало помещено в центр Земли;
- полярная ось направлена по оси магнитного диполя Земли (геомагнитной оси), проходящей через магнитные полюса;
- координата отсчитывается вдоль радиус-вектора, проведенного из центра Земли;
- полярный угол есть геомагнитная коширота (дополнение магнитной широты до );
- азимутальный угол совпадает с геомагнитной долготой, отсчитываемой к востоку от плоскости в западном полушарии, содержащей географический и геомагнитный полюсы.
Географические координаты северного магнитного полюса равны
В сферической геомагнитной системе координат склонение и
Формулы, связывающие географические и геомагнитные сферические координаты[1]:
В сферических геомагнитных координатах проще, чем в сферических географических координатах, описывать влияние геомагнитного поля на заряженные частицы околоземного пространства[1].
См. также
[править | править код]Примечания
[править | править код]Ссылки
[править | править код]- Weisstein, Eric W. Сферические координаты (англ.) на сайте Wolfram MathWorld.





































































