Нормальное распределение

Нормальное распределение
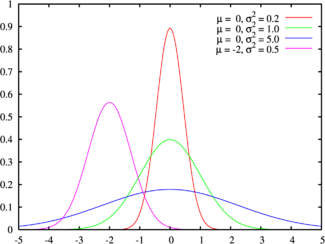Зеленая линия соответствует стандартному нормальному распределениюПлотность вероятности
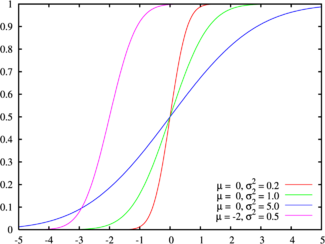Цвета на этом графике соответствуют графику наверхуФункция распределения
Обозначение	$N\left(\mu ,\sigma ^{2}\right)$
Параметры	μ — коэффициент сдвига (вещественный) σ > 0 — коэффициент масштаба (вещественный, строго положительный)
Носитель	$x\in \left(-\infty ;+\infty \right)$
Плотность вероятности	${\frac {1}{\sigma {\sqrt {2\pi }}}}\;\exp \left(-{\frac {\left(x-\mu \right)^{2}}{2\sigma ^{2}}}\right)$
Функция распределения	${\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sqrt {2\sigma ^{2}}}}\right)\right]$
Математическое ожидание	$\mu$
Медиана	$\mu$
Мода	$\mu$
Дисперсия	$\sigma ^{2}$
Коэффициент асимметрии	$0$
Коэффициент эксцесса	$0$
Дифференциальная энтропия	$\ln \left(\sigma {\sqrt {2\,\pi \,e}}\right)$
Производящая функция моментов	$M_{X}\left(t\right)=\exp \left(\mu \,t+{\frac {\sigma ^{2}t^{2}}{2}}\right)$
Характеристическая функция	$\phi _{X}\left(t\right)=\exp \left(\mu \,i\,t-{\frac {\sigma ^{2}t^{2}}{2}}\right)$

Норма́льное распределе́ние, также называемое распределением Гаусса или Гаусса — Лапласа — распределение вероятностей, которое в одномерном случае задаётся функцией плотности вероятности, совпадающей с функцией Гаусса:

$f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}$,

где параметр $\mu$ — математическое ожидание (среднее значение), медиана и мода распределения, а параметр $\sigma$ — среднеквадратическое отклонение, $\sigma ^{2}$ — дисперсия распределения.

Таким образом, одномерное нормальное распределение является двухпараметрическим семейством распределений, которое принадлежит экспоненциальному классу распределений. Многомерный случай описан в статье «Многомерное нормальное распределение».

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием $\mu =0$ и стандартным отклонением $\sigma =1.$

Общие сведения

Если величина является суммой многих случайных слабо взаимозависимых величин, каждая из которых вносит малый вклад относительно общей суммы, то центрированное и нормированное распределение такой величины при достаточно большом числе слагаемых стремится к нормальному распределению.

Это следует из центральной предельной теоремы теории вероятностей. В окружающем нас мире часто встречаются величины, значение которых определяется совокупностью многих независимых факторов. Этот факт, а также то, что распределение считалось типичным, обычным, привели к тому, что в конце XIX века стал использоваться термин «нормальное распределение». Нормальное распределение играет заметную роль во многих областях науки, например в математической статистике и статистической физике.

Случайная величина, имеющая нормальное распределение, называется нормальной, или гауссовской, случайной величиной.

Определения

Стандартное нормальное распределение

Наиболее простой случай нормального распределения — стандартное нормальное распределение — частный случай, когда $\mu =0$ и $\sigma =1.$ Его плотность вероятности равна:

$\varphi (x)={\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}x^{2}}.$

Множитель ${\frac {1}{\sqrt {2\pi }}}$ в выражении обеспечивает условие нормировки интеграла $\int \limits _{-\infty }^{+\infty }\varphi (x)\,dx=1$. Поскольку множитель ${\frac {1}{2}}$ в экспоненте обеспечивает дисперсию равную единице, то и стандартное отклонение равно 1. Функция симметрична в точке $x=0,$ её значение в ней максимально и равно ${\frac {1}{\sqrt {2\pi }}}.$ Точки перегиба функции: $x=+1$ и $x=-1.$

Гаусс называл стандартным нормальным распределение с $\sigma ^{2}=1/2,$ то есть:

$\varphi (x)={\frac {e^{-x^{2}}}{\sqrt {\pi }}}.$

Нормальное распределение с параметрами $\mu ,\sigma$

Каждое нормальное распределение — это вариант стандартного нормального распределения, область значений которого растягивается множителем $\sigma$ (стандартное отклонение) и переносится на $\mu$ (математическое ожидание):

$f(x\mid \mu ,\sigma ^{2})={\frac {1}{\sigma }}\varphi \left({\frac {x-\mu }{\sigma }}\right).$

$\mu ,\sigma$ являются параметрами нормального распределения. Плотность вероятности должна нормироваться ${\frac {1}{\sigma }},$ так что интеграл равен 1.

Если $Z$ — стандартная нормальная случайная величина, то величина $X=\sigma Z+\mu$ будет иметь нормальное распределение с математическим ожиданием $\mu$ и стандартным отклонением $\sigma .$ Наоборот, если $X$ — нормальная величина с параметрами $\mu$ и $\sigma ^{2},$ то $Z={\frac {X-\mu }{\sigma }}$ будет иметь стандартное нормальное распределение.

Если в экспоненте плотности вероятности раскрыть скобки и учитывать, что $1=\ln e$, то:

$f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}=e^{-{\frac {1}{2}}\left(2\ln \sigma +\ln 2\pi +({\frac {x-\mu }{\sigma }}\right)^{2})}=e^{-{\frac {1}{2}}\left({\frac {x^{2}}{\sigma ^{2}}}-2{\frac {\mu x}{\sigma ^{2}}}+2\ln \sigma +\ln 2\pi +{\frac {\mu ^{2}}{\sigma ^{2}}}\right)}.$

Таким образом, плотность вероятности каждого нормального распределения представляет собой экспоненту квадратичной функции:

$f(x)=e^{ax^{2}+bx+c},$

где $a=-{\frac {1}{2\sigma ^{2}}},\ b={\frac {\mu }{\sigma ^{2}}},\ c=-\left(\ln \sigma +{\frac {1}{2}}\ln 2\pi +{\frac {1}{2}}{\frac {\mu ^{2}}{\sigma ^{2}}}\right).$

Отсюда можно выразить среднее значение как $\mu =-{\frac {b}{2a}},$ а дисперсию как $\sigma ^{2}=-{\frac {1}{2a}}.$ Для стандартного нормального распределения $a=-1/2,$ $b=0$ и $c=-{\frac {1}{2}}\ln 2\pi .$

Обозначение

Плотность вероятности стандартного нормального распределения (с нулевым средним и единичной дисперсией) часто обозначается греческой буквой $\phi$ (фи). Также достаточно часто используется альтернативная формы греческой буквы фи $\varphi$.

Нормальное распределение часто обозначается $N(\mu ,\sigma ^{2}),$ или ${\mathcal {N}}(\mu ,\sigma ^{2})$. Если случайная величина $X$ распределена по нормальному закону со средним $\mu$ и вариацией $\sigma ^{2},$ то пишут:

$X\sim {\mathcal {N}}(\mu ,\sigma ^{2}).$

Функция распределения

Функция распределения стандартного нормального распределения обычно обозначается заглавной греческой буквой $\Phi$ (фи) и представляет собой интеграл:

$\Phi (x)={\frac {1}{\sqrt {2\pi }}}\int \limits _{-\infty }^{x}e^{-t^{2}/2}\,dt.$

С ней связана функция ошибок (интеграл вероятности) $\operatorname {erf} (x),$ дающий вероятность того, что нормальная случайная величина со средним 0 и вариацией 1/2 попадёт в отрезок $[-x,x]$:

$\operatorname {erf} (x)={\frac {2}{\sqrt {\pi }}}\int \limits _{0}^{x}e^{-t^{2}}\,dt.$

Эти интегралы не выражаются в элементарных функциях и называются специальными функциями. Многие их численные приближения известны. См. ниже.

Функции связаны, в частности, соотношением:

$\Phi (x)={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)\right]$.

Нормальное распределение с плотностью $f,$ средним $\mu$ и отклонением $\sigma$ имеет следующую функцию распределения:

$F(x)=\Phi \left({\frac {x-\mu }{\sigma }}\right)={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\right].$

Можно использовать функцию $Q(x)=1-\Phi (x)$ — она даст вероятность того, что значение стандартной нормальной случайной величины $X$ превысит $x$:

$P(X>x)$.

График стандартной нормальной функции распределения $\Phi$ имеет 2-кратную вращательную симметрию относительно точки (0;1/2), то есть $\Phi (-x)=1-\Phi (x).$ Её неопределенный интеграл равен:

$\int \Phi (x)\,dx=x\Phi (x)+\varphi (x)+C.$

Функция распределения стандартной нормальной случайной величины может быть разложена с помощью метода интегрирования по частям в ряд:

$\Phi (x)={\frac {1}{2}}+{\frac {1}{\sqrt {2\pi }}}\cdot e^{-x^{2}/2}\left[x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{3\cdot 5}}+\cdots +{\frac {x^{2n+1}}{(2n+1)!!}}+\cdots \right],$

где знак $!!$ означает двойной факториал.

Асимптотическое разложение функции распределения для больших $x$ может быть также произведено интегрированием по частям.

Стандартное отклонение

См. также: Интервальная оценка

Правило 68-95-99,7.
Для нормального распределения количество значений, отличающиеся от среднего на число, меньшее чем одно стандартное отклонение, составляют 68,27 % выборок. В то же время количество значений, отличающиеся от среднего на два стандартных отклонения, составляют 95,45 %, а на три стандартных отклонения — 99,73 %.

Около 68 % значений из нормального распределения находятся на расстоянии не более одного стандартного отклонения σ от среднего; около 95 % значений лежат расстоянии не более двух стандартных отклонений; и 99,7 % не более трёх. Этот факт является частным случаем правила 3 сигм для нормальной выборки.

Более точно, вероятность получить нормальное число в интервале между $\mu -n\sigma$ и $\mu +n\sigma$ равна:

$F(\mu +n\sigma )-F(\mu -n\sigma )=$

$\Phi (n)-\Phi (-n)=\operatorname {erf} \left({\frac {n}{\sqrt {2}}}\right).$

С точностью до 12 значащих цифр значения для $n=1,2,\ldots ,6$ приведены в таблице:

$n$	$p=F(\mu +n\sigma )-F(\mu -n\sigma )$	$1-p$	${\frac {1}{1-p}}$	OEIS
1	0,682689492137	0,317310507863	3,15148718753	A178647
2	0,954499736104	0,045500263896	21,9778945080	A110894
3	0,997300203937	0,002699796063	370,398347345	A270712
4	0,999936657516	0,000063342484	15787.1927673
5	0,999999426697	0,000000573303	1744277,89362
6	0,999999998027	0,000000001973	506797345,897

Свойства

Моменты

Моментами и абсолютными моментами случайной величины $X$ называются математические ожидания случайных величин $X^{p}$ и $\left|X\right|^{p},$ соответственно. Если математическое ожидание случайной величины $\mu =0,$ то эти параметры называются центральными моментами. В большинстве случаев представляют интерес моменты для целых $p.$

Если $X$ имеет нормальное распределение, то для неё существуют (конечные) моменты при всех $p$ с действительной частью больше −1. Для неотрицательных целых $p$ центральные моменты таковы:

$\mathbb {E} \left[X^{p}\right]={\begin{cases}0&p=2n+1,\\\sigma ^{p}\,\left(p-1\right)!!&p=2n.\end{cases}}$

Здесь $n$ — натуральное число, а запись $(p-1)!!$ означает двойной факториал числа $p-1,$ то есть (поскольку $p-1$ в данном случае нечётно) произведение всех нечётных чисел от 1 до $p-1.$

Центральные абсолютные моменты для неотрицательных целых $p$ таковы:

$\mathbb {E} \left[\left|X\right|^{p}\right]=\sigma ^{p}\,\left(p-1\right)!!\cdot \left.{\begin{cases}{\sqrt {\frac {2}{\pi }}}&p=2n+1,\\1&p=2n.\end{cases}}\right\}=\sigma ^{p}\cdot {\frac {2^{\frac {p}{2}}\Gamma \left({\frac {p+1}{2}}\right)}{\sqrt {\pi }}}.$

Последняя формула справедлива также для произвольных $p>-1$.

Преобразование Фурье и характеристическая функция

Преобразование Фурье нормальной плотности вероятности $f$ с математическим ожиданием $\mu$ стандартным отклонением $\sigma$ равно:

${\hat {f}}(t)=\int \limits _{-\infty }^{\infty }f(x)e^{-itx}\,dx=e^{-i\mu t}e^{-{\frac {1}{2}}(\sigma t)^{2}},$

где $i$ есть мнимая единица.

Если математическое ожидание $\mu =0,$ то первый множитель равен 1, и преобразование Фурье, с точностью до константы есть нормальная плотность вероятности на частотных интервалах, с математическим ожиданием равным 0 и стандартным отклонением $1/\sigma .$ В частности, стандартное нормальное распределение $\varphi$ есть собственная функция от преобразования Фурье.

В теории вероятности, преобразование Фурье плотности распределения действительной случайной величины $X$ близко связано с характеристической функцией $\varphi _{X}(t)$ этой величины, которая определена как математическое ожидание от $e^{itX}$ и является функцией вещественной переменной $t$ (частотный параметр преобразования Фурье). Определение может быть распространено и на комплексную переменную $t$. Соотношение записывается так:

$\varphi _{X}(t)={\hat {f}}(-t).$

Бесконечная делимость

Нормальное распределение является бесконечно делимым.

Если случайные величины $X_{1}$ и $X_{2}$ независимы и имеют нормальное распределение с математическими ожиданиями $\mu _{1}$ и $\mu _{2}$ и дисперсиями $\sigma _{1}^{2}$ и $\sigma _{2}^{2}$ соответственно, то $X_{1}+X_{2}$ также имеет нормальное распределение с математическим ожиданием $\mu _{1}+\mu _{2}$ и дисперсией $\sigma _{1}^{2}+\sigma _{2}^{2}.$

Отсюда вытекает, что нормальная случайная величина представима как сумма произвольного числа независимых нормальных случайных величин.

Максимальная энтропия

Нормальное распределение имеет максимальную дифференциальную энтропию среди всех непрерывных распределений, дисперсия которых не превышает заданную величину.

Правило трёх сигм для гауссовской случайной величины

Основная статья: Правило трёх сигм

График плотности вероятности нормального распределения и процент попадания случайной величины на отрезки, равные среднеквадратическому отклонению.

Правило трёх сигм ($3\sigma$) — практически все значения нормально распределённой случайной величины лежат в интервале:

$\left(\mu -3\sigma ;\mu +3\sigma \right),$

где $\mu =\mathbb {E} \xi$ — математическое ожидание и параметр нормальной случайной величины.

Более точно — приблизительно с вероятностью 0,9973 значение нормально распределённой случайной величины лежит в указанном интервале.

Моделирование нормальных псевдослучайных величин

При компьютерном моделировании, особенно при применении метода Монте-Карло, желательно использовать величины, распределенные по нормальному закону. Многие алгоритмы дают стандартные нормальные величины, так как нормальную величину $X\sim N(\mu ,\sigma ^{2})$ можно получить как:

$X=\mu +\sigma Z,$

где Z — стандартная нормальная величина.

Алгоритмы также используют различные преобразования равномерных величин. Простейшие приближённые методы моделирования основываются на центральной предельной теореме. Если сложить достаточно большое количество независимых одинаково распределённых величин с конечной дисперсией, то сумма будет иметь распределение, близкое к нормальному. Например, если сложить 100 независимых стандартно равномерно распределённых случайных величин, то распределение суммы будет приближённо нормальным.

Для программного генерирования нормально распределённых псевдослучайных величин предпочтительнее использовать преобразование Бокса — Мюллера. Оно позволяет генерировать одну нормально распределённую величину на базе одной равномерно распределённой.

Также существует алгоритм Зиккурат, который работает даже быстрее преобразования Бокса — Мюллера. Тем не менее, сложнее в реализации, но его применение оправдано в случаях, когда требуется генерирование очень большого числа неравномерно распределённых случайных чисел.

Нормальное распределение в природе и приложениях

Нормальное распределение часто встречается в природе. Например, следующие случайные величины хорошо моделируются нормальным распределением:

• отклонение при стрельбе;
• погрешности измерений (однако погрешности некоторых измерительных приборов имеют иное распределение);
• некоторые характеристики живых организмов в популяции.

Такое широкое распространение этого распределения связано с тем, что оно является бесконечно делимым непрерывным распределением с конечной дисперсией. Поэтому к нему в пределе приближаются некоторые другие, например биномиальное и пуассоновское. Этим распределением моделируются многие недетерминированные физические процессы.

Многомерное нормальное распределение используется при исследовании многомерных случайных величин (случайных векторов). Одним из многочисленных примеров таких приложений является исследование параметров личности человека в психологии и психиатрии.

Связь с другими распределениями

• Нормальное распределение является распределением Пирсона типа XI.
• Отношение пары независимых стандартных нормально распределенных случайных величин имеет распределение Коши. То есть, если случайная величина $X$ представляет собой отношение $X=Y/Z$ (где $Y$ и $Z$ — независимые стандартные нормальные случайные величины), то она будет обладать распределением Коши.
• Если $z_{1},\ldots ,z_{k}$ — совместно независимые стандартные нормальные случайные величины, то есть $z_{i}\sim N\left(0,1\right),$ то случайная величина $x=z_{1}^{2}+\ldots +z_{k}^{2}$ имеет распределение хи-квадрат с k степенями свободы.
• Если случайная величина $X$ подчинена логнормальному распределению, то её натуральный логарифм имеет нормальное распределение. То есть, если $X\sim \mathrm {LogN} \left(\mu ,\sigma ^{2}\right),$ то $Y=\ln \left(X\right)\sim \mathrm {N} \left(\mu ,\sigma ^{2}\right).$ И наоборот, если $Y\sim \mathrm {N} \left(\mu ,\sigma ^{2}\right),$ то $X=\exp \left(Y\right)\sim \mathrm {LogN} \left(\mu ,\sigma ^{2}\right).$
• Если $X_{1},X_{2},...,X_{n}$ независимые нормально распределенные случайные величины с математическими ожиданиями $\mu$ и дисперсиями $\sigma ^{2},$ то их выборочное среднее независимо от выборочного стандартного отклонения, а отношение следующих двух величин будет иметь t-распределение с ${\text{n}}-1$степенями свободы:

$t={\frac {{\overline {X}}-\mu }{S/{\sqrt {n}}}}={\frac {{\frac {1}{n}}(X_{1}+\cdots +X_{n})-\mu }{\sqrt {{\frac {1}{n(n-1)}}\left[(X_{1}-{\overline {X}})^{2}+\cdots +(X_{n}-{\overline {X}})^{2}\right]}}}\sim t_{n-1}.$

• Если $X_{1},X_{2},...,X_{n},$ $Y_{1},Y_{2},...,Y_{n}$ независимые стандартные нормальные случайные величины, то отношение нормированных сумм квадратов будет иметь распределение Фишера с (${\text{n}},$ ${\text{m}}$) степенями свободы:

$F={\frac {\left(X_{1}^{2}+X_{2}^{2}+\cdots +X_{n}^{2}\right)/n}{\left(Y_{1}^{2}+Y_{2}^{2}+\cdots +Y_{m}^{2}\right)/m}}\sim F_{n,m}.$

• Отношение квадратов двух стандартных нормальных случайных величин имеет распределение Фишера со степенями свободы $\left(1,1\right).$

История

Впервые нормальное распределение как предел биномиального распределения при $p={\tfrac {1}{2}}$ появилось в 1738 году во втором издании работы Муавра «Доктрина случайностей». Это было первое доказательство частного случая центральной предельной теоремы. В 1809 году Гаусс в сочинении «Теория движения небесных тел» ввёл это распределение как возникающее в результате многократных измерений движения небесных тел. Однако Гаусс вывел формулу для действительных случайных величин из принципа достижения максимума совместной плотности всех измерений в точке с координатами, равными среднему всех измерений. Этот принцип впоследствии подвергался критике. В 1812 году Лаплас в теореме Муавра — Лапласа обобщил результат Муавра для произвольного биномиального распределения, то есть для сумм одинаково распределённых независимых бинарных величин.

См. также

• Аддитивный белый гауссовский шум
• Логнормальное распределение
• Равномерное распределение
• Центральная предельная теорема
• Двумерное нормальное распределение
• Многомерное нормальное распределение
• Распределение хи-квадрат
• Статистический критерий
• Частотное распределение

Литература

• Королюк В. С., Портенко Н. И., Скороход А. В., Турбин А. Ф. Справочник по теории вероятностей и математической статистике. — М.: Наука, 1985. — 640 с.
• Halperin, Max; Hartley, Herman O.; Hoel, Paul G. Recommended Standards for Statistical Symbols and Notation. COPSS Committee on Symbols and Notation (англ.) // The American Statistician : journal. — 1965. — Vol. 19, no. 3. — P. 12—14. — doi:10.2307/2681417. — .
• McPherson, Glen. Statistics in Scientific Investigation: Its Basis, Application and Interpretation (англ.). — Springer-Verlag, 1990. — ISBN 978-0-387-97137-7.
• Bryc, Wlodzimierz. The Normal Distribution: Characterizations with Applications (англ.). — Springer-Verlag, 1995. — ISBN 978-0-387-97990-8.

Ссылки

• Таблица значений функции стандартного нормального распределения
• Онлайн расчёт вероятности нормального распределения