Тетраэдр Гурса

Тетраэдр Гурса — тетраэдральная фундаментальная область построения Витхоффа. Каждая грань тетраэдра представляет зеркальную гиперплоскость на 3-мерной поверхности — 3-сферы, евклидового 3-мерного пространства и гиперболического 3-мерного пространства. Коксетер назвал область именем Эдуара Гурса, который первым обратил внимание на эти области. Тетраэдр Гурса является расширением теории треугольников Шварца для построения Витхоффа на сфере.
Графическое представление
[править | править код]Тетраэдр Гурса может быть представлен графически тетраэдральным графом, который является двойственной конфигурацией фундаментальной области в виде тетраэдра. В этом графе каждый узел представляет грань (зеркало) тетраэдра Гурса. Каждое ребро помечено рациональным числом, соответствующим порядку отражения, который равен /двугранный угол.
4-вершинная диаграмма Коксетера — Дынкина представляет эти тетраэдральные графы со скрытыми рёбрами второго порядка. Если много рёбер имеют порядок 2, группа Коксетера может быть представлена скобочной нотацией[англ.].
Для существования тетраэдра Гурса каждый из подграфов с 3 вершинами этого графа, (p q r), (p u s), (q t u) и (r s t), должны соответствовать треугольнику Шварца.
Внешняя симметрия
[править | править код]
|

|
| Симметрия тетраэдра Гурса может быть тетраэдральной симметрией любой подгруппы симметрии, показанной в дереве цветом рёбер. | |
Расширенная симметрия тетраэдра Гурса является полупрямым произведением группы Коксетера симметрии и фундаментальной области симметрии (тетраэдра Гурса, в этом случае). Нотация Коксетера[англ.] поддерживает эту симметрию как вложенные скобки, наподобие [Y[X]], что означает полную группу Коксетера симметрии [X] с Y в качестве симметрии тетраэдра Гурса. Если Y является чистой зеркальной симметрией, группа будет представлять другую группу Коксетера отражений. Если имеется только одна простая удваивающая симметрия, Y может быть выражена явно, наподобие [[X]] с зеркальной или вращательной симметрией, в зависимости от контекста.
Расширенная симметрия каждого тетраэдра Гурса задана ниже. Наивысшая возможная симметрия у правильного тетраэдра, [3,3], и она достигается на призматической точечной группе [2,2,2], или [2[3,3]], и на паракомпактной гиперболической группе [3[3,3]].
См. симметрии тетраэдра для 7 симметрий низкого порядка тетраэдра.
Полное число решений
[править | править код]Последующие секции показывают все из полного набора решений тетраэдров Гурса для 3-сферы, евклидова 3-мерного пространства и гиперболического 3-мерного пространства. Расширенная симметрия каждого тетраэдра тоже указана.
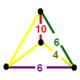
Цветные тетраэдральные диаграммы ниже являются вершинными фигурами всеусечённых[англ.] многогранников и сот из каждого семейства симметрий. Метки рёбер представляют порядки многоугольных граней, которые являются удвоенными порядками ветвей графа Коксетера. Двугранный угол ребра, помеченного 2n, равен . Жёлтые рёбра, помеченные цифрой 4, получаются из прямого угла (несвязанных) зеркал (узлов) диаграммы Коксетера.
(Конечные) решения на 3-сфере
[править | править код]
Решения для 3-сферы с плотностью 1: (однородные многогранники)
| Группа Коксетера и диаграмма |
[2,2,2] |
[p,2,2] |
[p,2,q] |
[p,2,p] |
[3,3,2] |
[4,3,2] |
[5,3,2] |
|---|---|---|---|---|---|---|---|
| Порядок группы симметрии | 16 | 8p | 4pq | 4p2 | 48 | 96 | 240 |
| Симметрии тетраэдра |
[3,3] (порядок 24) |
[2] (порядок 4) |
[2] (порядок 4) |
[2+,4] (порядок 8) |
[ ] (порядок 2) |
[ ]+ (порядок 1) |
[ ]+ (порядок 1) |
| Расширенные симметрии | [(3,3)[2,2,2]] =[4,3,3] |
[2[p,2,2]] =[2p,2,4] |
[2[p,2,q]] =[2p,2,2q] |
[(2+,4)[p,2,p]] =[2+[2p,2,2p]] |
[1[3,3,2]] =[4,3,2] |
[4,3,2] |
[5,3,2] |
| Порядок расширенных групп симметрии | 384 | 32p | 16pq | 32p2 | 96 | 96 | 240 |
| Тип графа | Линейный | Трёхлистный | |||
|---|---|---|---|---|---|
| Группа Коксетера и диаграмма |
Пяти- ячейный [3,3,3][англ.] |
Шестнадцати- ячейный [4,3,3][англ.] |
Двадцати- четырёхъ- ячейный [3,4,3][англ.]]] |
Шестисот- ячейный [5,3,3][англ.] [5,3,3][англ.] |
Полутессеракт [31,1,1][англ.] |
| Вершинная фигура всеусечённых однородных многогранников | |||||
| Тетраэдр | 
|

|

|
|

|
| Порядок группы симметрии |
120 | 384 | 1152 | 14400 | 192 |
| Тетраэдральная симметрия |
[2]+ (порядок 2) |
[ ]+ (порядок 1) |
[2]+ (порядок 2) |
[ ]+ (порядок 1) |
[3] (порядок 6) |
| Расширенная симметрия |
[2+[3,3,3]] |
[4,3,3] |
[2+[3,4,3]] |
[5,3,3] |
[3[31,1,1]] =[3,4,3] |
| Порядок группы расширенной симметрии | 240 | 384 | 2304 | 14400 | 1152 |
Решения в евклидовом 3-мерном пространстве
[править | править код]
Решения плотности 1: Выпуклые однородные соты[англ.]:
| Тип графа | Линейный | Трёхлистный | Кольцо | Призматический | Вырожденный | ||
|---|---|---|---|---|---|---|---|
| Группа Коксетера Диаграмма Коксетера |
[4,3,4][англ.] |
[4,31,1][англ.] |
[3[4]][англ.] |
[4,4,2] |
[6,3,2] |
[3[3],2] |
[∞,2,∞] |
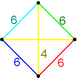
| Вершинная фигура всеусечённых сот | |||||||
| Тетраэдр | 
|

|
|
||||
| Тетраэдральная симметрия |
[2]+ (порядок 2) |
[ ] (порядок 2) |
[2+,4] (порядок 8) |
[ ] (порядок 2) |
[ ]+ (порядок 1) |
[3] (порядок 6) |
[2+,4] (порядок 8) |
| Расширенная симметрия |
[(2+)[4,3,4]] |
[1[4,31,1]] =[4,3,4] |
[(2+,4)[3[4]]] =[2+[4,3,4]] |
[1[4,4,2]] =[4,4,2] |
[6,3,2] |
[3[3[3],2]] =[3,6,2] |
[(2+,4)[∞,2,∞]] =[1[4,4]] |
Решения для гиперболических 3-пространств
[править | править код]Решения плотности 1: (Выпуклые однородные соты в гиперболическом пространстве[англ.]) (Компакт (группы симплексов Ланнера))
Решения в паракомпактных гиперболических 3-пространствах
[править | править код]

Решения плотности 1: (См. Паракомпакт (группы симплексов Козула))
Рациональные решения
[править | править код]Существует сотни рациональных решений для 3-сфер, включая эти 6 линейных графов, которые образуют многогранники Шлефли–Гесса, и 11 нелинейных:
Линейные графы
|
Графы «кольцо с хвостом»:
|
См. также
[править | править код]- Точечная группа симметрии для n-симплексных решений на (n-1)-сфере.
Примечания
[править | править код]Литература
[править | править код]- Coxeter H. C. M. Table 3: Schwarz’s Triangles // Regular Polytopes (book)[англ.]. — Third edition. — Dover Edition, 1973. — С. 280, Goursat's tetrahedra. — ISBN 0-486-61480-8.
- N.W. Johnson. The Theory of Uniform Polytopes and Honeycombs. — University of Toronto, 1966. — (Ph.D. Dissertation). Джонсон доказал, что перечисление тетраэдров Гурса Коксетером полно.
- Edouard Goursat. Sur les substitutions orthogonales et les divisions régulières de l'espace // Annales scientifiques de l'École Normale Supérieure. — 1889. — Вып. 6. — С. 9–102, 80–81 tetrahedra.
- Klitzing, Richard.Dynkin Diagrams Goursat tetrahedra
- N.W. Johnson. Главы 11,12,13 // Geometries and Transformations. — 2015.
- Johnson N. W., Kellerhals R., Ratcliffe J. G., Tschantz S. T. Transformation Groups // The size of a hyperbolic Coxeter simplex. — 1999. — Т. 4. — С. 329–353.
Для улучшения этой статьи желательно:
|











