Кватернион: различия между версиями
| [непроверенная версия] | [отпатрулированная версия] |
→Элементарные функции: \hat \mathbf{u} -> \frac{\mathbf{u}}{\left| \mathbf{u} \right|} (обозначение \mathbf{u} не было ранее определено) |
|||
| (не показана 81 промежуточная версия 38 участников) | |||
| Строка 1: | Строка 1: | ||
{{Универсальная карточка}} |
|||
'''Кватернио́ны''' (от {{lang-lat|quaterni}}, ''по четыре'') — система [[Гиперкомплексное число|гиперкомплексных чисел]], образующая [[векторное пространство]] [[Размерность пространства|размерностью]] четыре над [[Поле (алгебра)|полем]] [[вещественное число|вещественных чисел]]. |
'''Кватернио́ны''' (от {{lang-lat|quaterni}}, ''по четыре'') — система [[Гиперкомплексное число|гиперкомплексных чисел]], образующая [[векторное пространство]] [[Размерность пространства|размерностью]] четыре над [[Поле (алгебра)|полем]] [[вещественное число|вещественных чисел]]. |
||
Обычно обозначаются символом <math>\mathbb H</math>. Предложены [[Гамильтон, Уильям Роуан|Уильямом Гамильтоном]] в [[1843 |
Обычно обозначаются символом <math>\mathbb H</math>. Предложены [[Гамильтон, Уильям Роуан|Уильямом Гамильтоном]] в [[1843 год]]у. |
||
Кватернионы удобны для описания [[Изометрия (математика)|изометрий]] трёх- и четырёхмерного [[Евклидово пространство|евклидовых пространств]] |
Кватернионы удобны для описания [[Изометрия (математика)|изометрий]] трёх- и четырёхмерного [[Евклидово пространство|евклидовых пространств]] и поэтому получили широкое распространение в [[механика|механике]]. Также их используют в вычислительной математике — например, при создании трёхмерной графики<ref>[http://wat.gamedev.ru/articles/quaternions Кватернионы в программировании игр] {{Wayback|url=http://wat.gamedev.ru/articles/quaternions |date=20090725092721 }} ([[GameDev.ru]])</ref>. |
||
Также их используют в вычислительной математике, например, при создании трёхмерной графики.<ref>[http://wat.gamedev.ru/articles/quaternions Кватернионы в программировании игр] ([[GameDev.ru]])</ref> |
|||
[[Анри Пуанкаре]] писал о кватернионах: «Их появление дало мощный толчок развитию [[Общая алгебра|алгебры]]; исходя от них, наука пошла по пути обобщения понятия числа, придя к концепциям [[Матрица (математика)|матрицы]] и [[Линейное отображение|линейного оператора]], пронизывающим современную математику. Это была революция в арифметике, подобная той, которую сделал [[Лобачевский, Николай Иванович|Лобачевский]] в геометрии»<ref>{{статья|автор=Полак Л. С. |заглавие=Уильям Роуэн Гамильтон (к 150-летию со дня рождения) |издательство=АН СССР |издание=Труды Института истории естествознания |год=1956 |том=15 (История физ.-мат. наук) |страницы=273. }}</ref>. |
[[Анри Пуанкаре]] писал о кватернионах: «Их появление дало мощный толчок развитию [[Общая алгебра|алгебры]]; исходя от них, наука пошла по пути обобщения понятия числа, придя к концепциям [[Матрица (математика)|матрицы]] и [[Линейное отображение|линейного оператора]], пронизывающим современную математику. Это была революция в арифметике, подобная той, которую сделал [[Лобачевский, Николай Иванович|Лобачевский]] в [[Геометрия Лобачевского|геометрии]]»<ref>{{статья|автор=Полак Л. С. |заглавие=Уильям Роуэн Гамильтон (к 150-летию со дня рождения) |издательство=АН СССР |издание=Труды Института истории естествознания |год=1956 |том=15 (История физ.-мат. наук) |страницы=273. }}</ref>. |
||
== Определения == |
== Определения == |
||
=== Стандартное === |
=== Стандартное === |
||
Кватернионы можно определить как сумму |
|||
Кватернионы можно определить как формальную сумму <math>a+bi+cj+dk,</math> где <math>a, b, c, d</math> — вещественные числа, а <math>i, j, k</math> — ''[[Мнимая единица|мнимые единицы]]'' со следующим свойством: <math>i^2=j^2=k^2=ijk=-1i=-1j=-1k</math>. Таким образом<!-- следовательно -->, таблица умножения ''[[базис]]ных кватернионов'' — <math>1, i, j, k</math> — выглядит так: |
|||
: <math>q=a+bi+cj+dk</math> |
|||
где <math>a, b, c, d</math> — вещественные числа |
|||
<math> |
|||
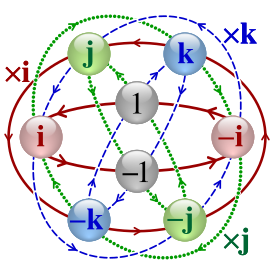
[[File:Quaternion-multiplication-cayley-3d-with-legend.png|thumb|350px|Графическое представление таблицы умножения базисных кватернионов (цвет шара определяет первый множитель, цвет выходящей стрелки - второй множитель, стрелка указывает на результат умножения)]] |
|||
\begin{matrix} |
|||
: <math>i, j, k</math> — ''[[Мнимая единица|мнимые единицы]]'' со следующим свойством: <math>i^2=j^2=k^2=ijk=-1</math>, при этом результат их попарного произведения зависит от порядка следования (не является [[коммутативная операция|коммутативным]]): <math>ij=k</math>, a <math>ji=-k</math>. |
|||
& \times & \mathbf1 & \mathbf{i} & \mathbf{j} & \mathbf{k} \\ |
|||
<center> |
|||
& \mathbf1 & \,1 & \,i & \,j & \,k \\ |
|||
{| class="wikitable" |
|||
& \mathbf{i} & \,i & \,-1 & \,k & \,-j \\ |
|||
|+ Таблица умножения базисных кватернионов <math>1, i, j, k</math> |
|||
& \mathbf{j} & \,j & \,-k & \,-1 & \,i \\ |
|||
!X |
|||
& \mathbf{k} & \,k & \,j & \,-i & \,-1 \\ |
|||
!1 |
|||
\end{matrix} |
|||
!i |
|||
</math> |
|||
!j |
|||
!k |
|||
Например, <math>ij=k</math>, a <math>ji=-k</math>. |
|||
|- |
|||
|'''1''' |
|||
|1 |
|||
|i |
|||
|j |
|||
|k |
|||
|- |
|||
|'''i''' |
|||
|i |
|||
| -1 |
|||
|k |
|||
| -j |
|||
|- |
|||
|'''j''' |
|||
|j |
|||
| -k |
|||
| -1 |
|||
|i |
|||
|- |
|||
|'''k''' |
|||
|k |
|||
|j |
|||
| -i |
|||
| -1 |
|||
|} |
|||
</center> |
|||
=== Как вектор и скаляр === |
=== Как вектор и скаляр === |
||
| Строка 28: | Строка 54: | ||
Операции сложения определены следующим образом: |
Операции сложения определены следующим образом: |
||
: <math>\left(a, \vec{u} \right)+ \left(b , \vec{v}\right)= \left(a + b , \vec{u} + \vec{v}\right) </math> |
: <math>\left(a, \vec{u} \right)+ \left(b , \vec{v}\right)= \left(a + b , \vec{u} + \vec{v}\right). </math> |
||
Произведение определяется следующим образом: |
Произведение определяется следующим образом: |
||
: <math>\left(a, \vec{u}\right)\left(b, \vec{v}\right)= \left(ab - \vec{u}\cdot\vec{v}, a\vec{v} + b\vec{u} + \vec{u}\times\vec{v}\right)</math> |
: <math>\left(a, \vec{u}\right)\left(b, \vec{v}\right)= \left(ab - \vec{u}\cdot\vec{v}, a\vec{v} + b\vec{u} + \vec{u}\times\vec{v}\right),</math> |
||
где <math>\cdot</math> обозначает [[скалярное произведение]], а <math>\times</math> — [[векторное произведение]]. |
где <math>\cdot</math> обозначает [[скалярное произведение]], а <math>\times</math> — [[векторное произведение]]. |
||
В частности |
В частности: |
||
: <math>\left(a, 0\right)\left(0, \vec{v}\right)=\left(0, \vec{v}\right)\left(a, 0 \right)= \left(0, a\vec{v}\right)</math> |
: <math>\left(a, 0\right)\left(0, \vec{v}\right)=\left(0, \vec{v}\right)\left(a, 0 \right)= \left(0, a\vec{v}\right),</math> |
||
: <math>\left(a, 0\right)\left(b, 0\right)=\left(ab, 0\right)</math> |
: <math>\left(a, 0\right)\left(b, 0\right)=\left(ab, 0\right),</math> |
||
: <math>\left(0, \vec{u} \right)\left(0, \vec{v}\right)= \left( - \vec{u}\cdot\vec{v} , \vec{u}\times\vec{v}\right)</math> |
: <math>\left(0, \vec{u} \right)\left(0, \vec{v}\right)= \left( - \vec{u}\cdot\vec{v} , \vec{u}\times\vec{v}\right).</math> |
||
Заметим, что: |
Заметим, что: |
||
| Строка 71: | Строка 97: | ||
*: <math> |
*: <math> |
||
\left|q \right| ^ 4 = |
\left|q \right| ^ 4 = |
||
\det Q |
\det Q. |
||
</math> |
</math> |
||
==== Комплексными матрицами ==== |
==== Комплексными матрицами ==== |
||
Альтернативно, кватернионы можно определить как комплексные матрицы следующего вида с обычными матричными произведением и суммой: |
Альтернативно, кватернионы можно определить как комплексные матрицы следующего вида с обычными матричными произведением и суммой{{sfn|Stillwell|2008|p=7}}: |
||
: <math>\begin{pmatrix} \;\;\alpha & \beta \\ -\bar \beta & \bar \alpha \end{pmatrix}=\begin{pmatrix} \;\;a+bi & c+di \\ -c+di & a-bi \end{pmatrix},</math> |
: <math>\begin{pmatrix} \;\;\alpha & \beta \\ -\bar \beta & \bar \alpha \end{pmatrix}=\begin{pmatrix} \;\;a+bi & c+di \\ -c+di & a-bi \end{pmatrix},</math> |
||
здесь <math>\bar \alpha</math> и <math>\bar \beta</math> обозначают комплексно-сопряжённые числа к <math>\alpha</math> и <math>\beta</math>. |
здесь <math>\bar \alpha</math> и <math>\bar \beta</math> обозначают комплексно-сопряжённые числа к <math>\alpha</math> и <math>\beta</math>. |
||
| Строка 89: | Строка 115: | ||
*: <math> |
*: <math> |
||
\left|q \right| ^ 2 = |
\left|q \right| ^ 2 = |
||
\det Q |
\det Q. |
||
</math> |
</math> |
||
== Связанные объекты и операции == |
== Связанные объекты и операции == |
||
| Строка 99: | Строка 125: | ||
=== Сопряжение === |
=== Сопряжение === |
||
Для кватерниона <math>q |
Для кватерниона <math>q</math> ''сопряжённым'' называется{{sfn|Stillwell|2008|p=9}}: |
||
: <math>\bar q=a-bi-cj-dk</math> |
: <math>\bar q=a-bi-cj-dk.</math> |
||
Сопряжённое произведение есть произведение сопряжённых в обратном порядке: |
Сопряжённое произведение есть произведение сопряжённых в обратном порядке{{sfn|Stillwell|2008|p=10}}: |
||
: <math> \overline {pq} = \bar q \bar p </math> |
: <math> \overline {pq} = \bar q \bar p. </math> |
||
Для кватернионов справедливо равенство |
Для кватернионов справедливо равенство |
||
: <math> \overline {p} =-\frac 12 (p+ipi+jpj+kpk) </math> |
: <math> \overline {p} =-\frac 12 (p+ipi+jpj+kpk). </math> |
||
=== Модуль === |
=== Модуль === |
||
Так же, как и для комплексных чисел, |
Так же, как и для комплексных чисел{{sfn|Stillwell|2008|p=8}}, |
||
: <math> \left|q \right| =\sqrt{q\bar q}=\sqrt{a^2+b^2+c^2+d^2}</math> |
: <math> \left|q \right| =\sqrt{q\bar q}=\sqrt{a^2+b^2+c^2+d^2}</math> |
||
| Строка 125: | Строка 151: | ||
=== Обращение умножения (деление) === |
=== Обращение умножения (деление) === |
||
Кватернион, обратный по умножению к <math>q</math>, вычисляется так: |
Кватернион, обратный по умножению к <math>q</math>, вычисляется так{{sfn|Stillwell|2008|p=9}}: |
||
<math> q^{-1} = \frac {\bar q} {\left|q \right| ^ 2} </math>. |
<math> q^{-1} = \frac {\bar q} {\left|q \right| ^ 2} </math>. |
||
== Алгебраические свойства == |
== Алгебраические свойства == |
||
Множество кватернионов является примером [[Тело (алгебра)|тела]], то есть кольца с делением и единицей. |
|||
Четыре базисных кватерниона и четыре противоположных им по знаку образуют по умножению |
|||
[[группа (математика)|группу]] кватернионов ([[порядок группы|порядка]] 8). |
|||
Обозначается: |
|||
: <math> Q_8 = \left\{\pm 1, \pm i, \pm j, \pm k \right\} </math>. |
|||
Множество кватернионов является примером кольца с делением. |
|||
Множество кватернионов образует четырёхмерную ассоциативную алгебру с делением |
Множество кватернионов образует четырёхмерную ассоциативную алгебру с делением |
||
над полем вещественных (но не комплексных) чисел. |
над полем вещественных (но не комплексных) чисел. |
||
По [[Теорема Фробениуса|теореме Фробениуса]] тела |
|||
<math> \mathbb R</math>, <math> \mathbb C</math>, <math> \mathbb H</math> |
<math> \mathbb R</math>, <math> \mathbb C</math>, <math> \mathbb H</math> |
||
являются единственными конечномерными ассоциативными алгебрами с делением |
являются единственными конечномерными ассоциативными алгебрами с делением |
||
над полем вещественных чисел |
над полем вещественных чисел. |
||
Некоммутативность умножения кватернионов приводит к неожиданным последствиям. |
Некоммутативность умножения кватернионов приводит к неожиданным последствиям. |
||
| Строка 147: | Строка 169: | ||
q^2 + 1 = 0 </math> |
q^2 + 1 = 0 </math> |
||
имеет бесконечно много решений — это все единичные чисто векторные кватернионы. |
имеет бесконечно много решений — это все единичные чисто векторные кватернионы. |
||
Четыре базисных кватерниона и четыре противоположных им по знаку образуют по умножению |
|||
[[группа (математика)|группу]] кватернионов ([[порядок группы|порядка]] 8). |
|||
Обозначается: |
|||
: <math> Q_8 = \left\{\pm 1, \pm i, \pm j, \pm k \right\}. </math> |
|||
== Кватернионы и повороты пространства == |
== Кватернионы и повороты пространства == |
||
| Строка 152: | Строка 179: | ||
[[Файл:Rotating gimbal-xyz.gif|thumb|240px|Организация [[Шесть степеней свободы|трёх степеней свободы]], но окончательная свобода меньших колец зависит от положения больших колец]] |
[[Файл:Rotating gimbal-xyz.gif|thumb|240px|Организация [[Шесть степеней свободы|трёх степеней свободы]], но окончательная свобода меньших колец зависит от положения больших колец]] |
||
Кватернионы, рассматриваемые как [[Алгебра над полем|алгебра]] над <math>\ |
Кватернионы, рассматриваемые как [[Алгебра над полем|алгебра]] над <math>\mathbb R</math>, образуют четырёхмерное вещественное [[векторное пространство]]. Любой поворот этого пространства относительно <math>0</math> может быть записан в виде <math>q\mapsto \xi q \zeta</math>, где <math>\xi</math> и <math>\zeta</math> — пара единичных кватернионов, при этом пара <math>\left(\xi,\zeta\right)</math> определяется с точностью до знака, то есть один поворот определяют в точности две пары — <math>\left(\xi,\zeta\right)</math> и <math>\left(-\xi,-\zeta\right)</math>. Из этого следует, что [[группа Ли]] <math>\text{SO}\left(\R,4\right)</math> [[поворот]]ов <math>\R^4</math> есть [[факторгруппа]] <math>S^3\times S^3/\Z_2</math>, где <math>S^3</math> обозначает мультипликативную группу единичных кватернионов. |
||
Чисто векторные кватернионы образуют трёхмерное вещественно векторное пространство. Любой поворот пространства чисто векторных кватернионов относительно <math>0</math> может быть записан в виде <math>u\mapsto \xi u \bar\xi</math>, где <math>\xi</math> — некоторый единичный кватернион. Соответственно, <math>\text{SO}\left(\R,3\right)=S^3/\Z_2</math>, в частности, <math>\text{SO}\left(\R,3\right)</math> [[диффеоморфизм|диффеоморфно]] <math>\R \mathrm{P}^3</math>. |
Чисто векторные кватернионы образуют трёхмерное вещественно векторное пространство. Любой поворот пространства чисто векторных кватернионов относительно <math>0</math> может быть записан в виде <math>u\mapsto \xi u \bar\xi</math>, где <math>\xi</math> — некоторый единичный кватернион. Соответственно, <math>\text{SO}\left(\R,3\right)=S^3/\Z_2</math>, в частности, <math>\text{SO}\left(\R,3\right)</math> [[диффеоморфизм|диффеоморфно]] <math>\R \mathrm{P}^3</math>. |
||
| Строка 160: | Строка 187: | ||
\left\|z \right\| = \left |z \right | ^ 2 </math>. |
\left\|z \right\| = \left |z \right | ^ 2 </math>. |
||
''Целыми'' |
''Целыми'' [[Кватернион Гурвица|по Гурвицу]] принято называть кватернионы <math>a + bi + cj + dk</math> такие, что все <math>2a, 2b, 2c, 2d</math> — [[целое число|целые]] и одинаковой чётности. |
||
Целый кватернион называется |
Целый кватернион называется |
||
| Строка 174: | Строка 201: | ||
=== Целые единичные кватернионы === |
=== Целые единичные кватернионы === |
||
Существует 24 целых единичных кватерниона: |
Существует 24 целых единичных кватерниона: |
||
: <math> \pm 1</math>; |
: <math> \pm 1</math>; <math> \pm i</math>; <math> \pm j</math>; <math> \pm k</math>; <math> \frac {\pm 1 \pm i \pm j \pm k } {2}. </math> |
||
Они образуют группу по умножению, лежат в вершинах правильного |
Они образуют группу по умножению, лежат в вершинах правильного 4-мерного многогранника — [[Двадцатичетырёхъячейник|3-кубооктаэдра]] (не путать с 3-мерным многогранником-[[кубооктаэдр]]ом). |
||
=== Разложение на простые сомножители === |
=== Разложение на простые сомножители === |
||
| Строка 228: | Строка 255: | ||
: <math> |
: <math> |
||
\operatorname {sgn}\, q = |
\operatorname {sgn}\, q = |
||
\frac {q} {\left|q \right|} |
\frac {q} {\left|q \right|}. |
||
</math> |
</math> |
||
Аргумент кватерниона — это угол в четырёхмерном пространстве между кватернионом и вещественной |
Аргумент кватерниона — это угол в четырёхмерном пространстве между кватернионом и вещественной единицей: |
||
: <math> \arg q = \arccos \frac {a} {\left|q \right|} </math> |
: <math> \arg q = \arccos \frac {a} {\left|q \right|}. </math> |
||
В дальнейшем используется представление заданного кватерниона <math>q</math> в виде |
В дальнейшем используется представление заданного кватерниона <math>q</math> в виде |
||
: <math>q = a + \left| \mathbf{u} \right| \mathrm{i} = \left| q \right| \mathrm{e}^{\mathrm{i}\,\mathrm{arg}\,q}</math> |
: <math>q = a + \left| \mathbf{u} \right| \mathrm{i} = \left| q \right| \mathrm{e}^{\mathrm{i}\,\mathrm{arg}\,q}.</math> |
||
Здесь <math>a</math> — вещественная часть кватерниона, <math>\mathrm{i} = \left| \mathbf{u} \right|^{-1} \mathbf{u}</math>. При этом <math>\mathrm{i}^2 = -1</math>, поэтому проходящая через <math>q</math> и вещественную прямую плоскость имеет структуру алгебры комплексных чисел, что позволяет перенести на случай кватернионов произвольные аналитические функции. Они удовлетворяют стандартным соотношениям, если все аргументы имеют вид <math>a+b\mathrm{i}</math> для фиксированного единичного вектора <math>\mathrm{i}</math>. В случае если требуется рассматривать кватернионы с разным направлением, формулы значительно усложняются, в силу некоммутативности алгебры кватернионов. |
Здесь <math>a</math> — вещественная часть кватерниона, <math>\mathrm{i} = \left| \mathbf{u} \right|^{-1} \mathbf{u}</math>. При этом <math>\mathrm{i}^2 = -1</math>, поэтому проходящая через <math>q</math> и вещественную прямую плоскость имеет структуру алгебры комплексных чисел, что позволяет перенести на случай кватернионов произвольные аналитические функции. Они удовлетворяют стандартным соотношениям, если все аргументы имеют вид <math>a+b\mathrm{i}</math> для фиксированного единичного вектора <math>\mathrm{i}</math>. В случае если требуется рассматривать кватернионы с разным направлением, формулы значительно усложняются, в силу некоммутативности алгебры кватернионов. |
||
| Строка 246: | Строка 273: | ||
: <math> |
: <math> |
||
\ |
\mathrm{e}^q = \mathrm{e}^a \left( |
||
\cos \left|\mathbf{u} \right| + \ |
\cos \left|\mathbf{u} \right| + \frac{\mathbf{u}}{\left| \mathbf{u} \right|} \sin \left| \mathbf{u} \right| |
||
\right) |
\right) |
||
</math> |
</math> |
||
: <math> |
: <math> |
||
\ln q = \ln \left|q \right| + \ |
\ln q = \ln \left|q \right| + \frac{\mathbf{u}}{\left| \mathbf{u} \right|} \arg q |
||
</math> |
</math> |
||
Отметим, что, как обычно в комплексном анализе, логарифм оказывается определён лишь с точностью до <math>2\pi \ |
Отметим, что, как обычно в комплексном анализе, логарифм оказывается определён лишь с точностью до <math>2\pi \frac{\mathbf{u}}{\left| \mathbf{u} \right|}</math>. |
||
; Тригонометрические функции |
; Тригонометрические функции |
||
| Строка 265: | Строка 292: | ||
\operatorname {ch} \left|\mathbf{u} \right| |
\operatorname {ch} \left|\mathbf{u} \right| |
||
+ |
+ |
||
\cos a \, \operatorname {sh} \left|\mathbf{u} \right| |
\frac{\mathbf{u}}{\left| \mathbf{u} \right|} \cos a \, \operatorname {sh} \left|\mathbf{u} \right| |
||
</math> |
</math> |
||
| Строка 274: | Строка 301: | ||
\operatorname {ch} \left|\mathbf{u} \right| |
\operatorname {ch} \left|\mathbf{u} \right| |
||
- |
- |
||
\sin a \, \operatorname {sh} \left|\mathbf{u} \right| |
\frac{\mathbf{u}}{\left| \mathbf{u} \right|} \sin a \, \operatorname {sh} \left|\mathbf{u} \right| |
||
</math> |
</math> |
||
| Строка 281: | Строка 308: | ||
= \frac{\sin q}{\cos q} |
= \frac{\sin q}{\cos q} |
||
</math> |
</math> |
||
=== Линейное отображение === |
|||
Отображение <math>f:\mathbb H\rightarrow \mathbb H</math> |
|||
алгебры кватернионов называется линейным, если верны равенства |
|||
: <math>f(x+y)=f(x)+f(y)</math> |
|||
: <math>f(ax)=af(x)</math> |
|||
: <math>x,y\in\mathbb H, a\in\mathbb R</math> |
|||
где <math>\mathbb R</math> — поле действительных чисел. |
|||
Если <math>f</math> является линейным отображением алгебры кватернионов, |
|||
то для любых <math>a, b\in\mathbb H</math> отображение |
|||
: <math>(afb)(x)=af(x)b</math> |
|||
является линейным отображением. |
|||
Если <math>f</math> — тождественное отображение (<math>f(x)=x</math>), |
|||
то для любых <math>a, b\in\mathbb H</math> |
|||
мы можем отождествить [[тензорное произведение]] <math>a\otimes b</math> с отображением |
|||
: <math>(a\otimes b)\circ x=axb</math> |
|||
Для любого линейного отображения |
|||
<math>f:\mathbb H\rightarrow \mathbb H</math> |
|||
существует [[тензор]] <math>a\in\mathbb H\otimes\mathbb H</math>, |
|||
<math>a=a_{s0}\otimes a_{s1}</math>, |
|||
такой, что |
|||
: <math>f(x)=a\circ x=(a_{s0}\otimes a_{s1})\circ x=a_{s0}xa_{s1}</math> |
|||
В приведённых выше равенствах предполагается суммирование по индексу <math>s</math>. |
|||
Поэтому мы можем отождествить линейное отображение <math>f</math> |
|||
и тензор <math>a</math>. |
|||
=== Регулярные функции === |
=== Регулярные функции === |
||
| Строка 300: | Строка 352: | ||
University of York, 1977.</ref>. |
University of York, 1977.</ref>. |
||
=== Дифференцирование отображений === |
|||
=== Производная Гато === |
|||
{{main|Кватернионный анализ}} |
{{main|Кватернионный анализ}} |
||
Непрерывное отображение |
|||
[[Производная Гато]] функции кватернионного переменного |
|||
<math>f:\mathbb H\rightarrow \mathbb H</math> |
|||
определена согласно формуле |
|||
называется дифференцируемым |
|||
: <math>\partial f(x)(a)=\lim_{t\to 0}(t^{-1}(f(x+ta)-f(x)))</math> |
|||
на множестве <math>U\subset \mathbb H</math>, |
|||
если в каждой точке <math>x\in U</math> |
|||
изменение отображения <math>f</math> может быть представлено в виде |
|||
: <math>f(x+h)-f(x)=\frac{d f(x)}{d x}\circ h+o(h)</math> |
|||
где |
|||
: <math>\frac{d f(x)}{d x}:\mathbb H\rightarrow\mathbb H</math> |
|||
линейное отображение алгебры кватернионов <math>\mathbb H</math> и |
|||
<math>o:\mathbb H\rightarrow \mathbb H</math> |
|||
такое непрерывное отображение, что |
|||
: <math>\lim_{a\rightarrow 0}\frac{|o(a)|}{|a|}=0</math> |
|||
Линейное отображение |
|||
<math>\frac{d f(x)}{d x}</math> |
|||
называется производной отображения <math>f</math>. |
|||
Производная может быть представлена в |
|||
Производная Гато является [[Аддитивное отображение|аддитивным отображением]] |
|||
виде<ref>Выражение <math>\frac{d_{sp} f(x)}{d x} </math> |
|||
приращения аргумента и может быть представлена в |
|||
не является дробью и должно восприниматься как единый символ. |
|||
виде<ref>Выражение <math>\frac{{}_{(s)p}\partial f(x)}{\partial x} </math> |
|||
Данное обозначение предложено для совместимости с обозначением производной. |
|||
не является дробью и должно восприниматься как символ оператора. |
|||
Значение выражения <math>\frac{d_{sp} f(x)}{d x} </math> при заданном <math>x</math> |
|||
Данное обозначение предложено для того, чтобы сохранить преемственность |
|||
является кватернионом.</ref> |
|||
с классическим анализом.</ref> |
|||
: <math>\ |
: <math>\frac{d f(x)}{d x}= |
||
\frac{{} |
\frac{d_{s0} f(x)}{d x} |
||
\otimes |
|||
\frac{d_{s1} f(x)}{d x} |
|||
</math> |
|||
Соответственно дифференциал отображения <math>f</math> имеет вид |
|||
: <math>df=\frac{d f(x)}{d x}\circ dx= |
|||
\left( |
|||
\frac{d_{s0} f(x)}{d x} |
|||
\otimes |
|||
\frac{d_{s1} f(x)}{d x}\right)\circ dx= |
|||
\frac{d_{s0} f(x)}{d x} |
|||
dx |
dx |
||
\frac{{} |
\frac{d_{s1} f(x)}{d x} |
||
</math> |
</math> |
||
Здесь предполагается суммирование по индексу <math>s</math>. Число слагаемых |
Здесь предполагается суммирование по индексу <math>s</math>. Число слагаемых |
||
зависит от выбора функции <math>f</math>. Выражения |
зависит от выбора функции <math>f</math>. Выражения |
||
<math>\frac{{} |
<math>\frac{d_{s0}d f(x)}{d x}</math> и |
||
<math>\frac{{} |
<math>\frac{d_{s1} f(x)}{d x}</math> называются |
||
компонентами производной. |
компонентами производной. |
||
Для произвольного кватерниона <math>a</math> верно равенство |
|||
: <math>\frac{d f(x)}{d x}\circ a=\lim_{t\to 0}(t^{-1}(f(x+ta)-f(x)))</math> |
|||
== Виды умножений == |
== Виды умножений == |
||
| Строка 331: | Строка 409: | ||
=== Евклидово умножение === |
=== Евклидово умножение === |
||
Отличается от общепринятого тем, что вместо первого сомножителя |
Отличается от общепринятого тем, что вместо первого сомножителя берётся сопряжённый к нему: <math>\bar p q</math>. |
||
Оно также некоммутативно. |
Оно также некоммутативно. |
||
| Строка 363: | Строка 441: | ||
== Из истории == |
== Из истории == |
||
[[Файл:William Rowan Hamilton Plaque - geograph.org.uk - 347941.jpg|thumb|<center>Памятная табличка на мосту Брум Бридж в [[Дублин]]е: «Здесь на прогулке, 16 октября 1843 |
[[Файл:William Rowan Hamilton Plaque - geograph.org.uk - 347941.jpg|thumb|<center>Памятная табличка на мосту Брум Бридж в [[Дублин]]е: «Здесь на прогулке, 16 октября 1843 года, во вспышке гения, сэр [[Гамильтон, Уильям Роуан|Уильям Роуэн Гамильтон]] открыл формулу перемножения кватернионов»<ref>В письме своему сыну Арчибальду от 5 августа 1865 года Гамильтон пишет: «…Но, конечно, надпись уже стёрлась» (''Л. С. Полак'' Вариационные принципы механики, их развитие и применение в физике.— М.: Физматгиз, 1960.— С.103-104)</ref></center>]] |
||
Система кватернионов была впервые опубликована [[Гамильтон, Уильям Роуан|Гамильтоном]] в [[1843 год]]у. Историки науки также обнаружили наброски по этой теме в неопубликованных рукописях [[Карл Гаусс|Гаусса]], относящихся к [[1819]]—[[1820 год]]ам<ref>{{книга |автор=[[Николя Бурбаки|Бурбаки Н.]]. |заглавие=Архитектура математики. Очерки по истории математики |место=М. |издательство=Иностранная литература |год=1963 |страницы=68 }}</ref>. Также кватернионы рассматривал Эйлер. [[Родриг, Олинд|Б. О. Родриг]] (1840 год) при рассмотрении поворотов абсолютно твёрдого тела вывел правила умножения кватернионов<ref>{{статья |автор = Rodrigues Olinde |заглавие = Геометрические законы, управляющие перемещениями твёрдой системы в пространстве, и изменение координат, возникающее в результате этих перемещений, рассматриваемые независимо от причин, которые могут их вызвать|оригинал = Des lois géométriques qui régissent les déplacements d'un système solide dans l'espace, et de la variation des coordonnées provenant de ces déplacements considérés indépendamment des causes qui peuvent les produire|ссылка = https://books.google.com/books?id=f9ZGAAAAcAAJ&pg=PA380|издание = Journal de Mathématiques Pures et Appliquées|год =1840 |том = 5|страницы = 380—440 |doi = |pmid = |bibcode = |arxiv = |ref = }}</ref>{{sfn|Березин, Курочкин и Толкачёв|2003|с=5}}. |
|||
Система кватернионов была впервые опубликована [[Гамильтон, Уильям Роуан|Гамильтоном]] в [[1843 год]]у. |
|||
Историки науки также обнаружили наброски по этой теме в неопубликованных рукописях [[Карл Гаусс|Гаусса]], относящихся к [[1819]]—[[1820 год]]ам.<ref>{{книга |
|||
|автор=[[Николя Бурбаки|Бурбаки Н.]]. |заглавие=Архитектура математики. Очерки по истории математики |
|||
|место=М. |издательство=Иностранная литература |год=1963 |страницы=68 }}</ref> |
|||
Бурное и чрезвычайно плодотворное развитие комплексного анализа в |
Бурное и чрезвычайно плодотворное развитие комплексного анализа в XIX веке стимулировало у математиков интерес к следующей задаче: найти новый вид чисел, аналогичный по свойствам [[комплексное число|комплексным]], но содержащий не одну, а две мнимые единицы. Предполагалось, что такая модель будет полезна при решении пространственных задач математической физики. Однако работа в этом направлении оказалась безуспешной{{sfn|Березин, Курочкин и Толкачёв|2003|с=5}}. |
||
Новый вид чисел был обнаружен ирландским математиком [[Гамильтон, Уильям Роуэн|Уильямом Гамильтоном]] в [[1843 |
Новый вид чисел был обнаружен ирландским математиком [[Гамильтон, Уильям Роуэн|Уильямом Гамильтоном]] (который также занимался указанной задачей) в [[1843 год в науке|1843 году]], и он содержал не две, как ожидалось, а три мнимые единицы. Гамильтон работал сначала с ''дуплетами'' (точками на плоскости) и легко получил правила для умножения соответствующие комплексным числам, но для точек в пространстве (''триплеты'') не мог получить никакой формулы умножения для таких наборов. В конце концов решил попробовать ''четвёрки'' — точки в четырёхмерном пространстве. Эти числа Гамильтон назвал ''кватернионами''{{sfn|Мищенко и Соловьёв|1983|с=11—12}}. Позднее [[Фробениус, Фердинанд Георг|Фробениус]] строго доказал (1877) [[Теорема Фробениуса|теорему]], согласно которой расширить комплексное [[Поле (алгебра)|поле]] до поля или [[Тело (алгебра)|тела]] с двумя мнимыми единицами невозможно{{sfn|Мищенко и Соловьёв|1983|с=15}}. |
||
Несмотря на необычные свойства новых чисел (их некоммутативность), эта модель довольно быстро принесла практическую пользу. [[Максвелл, Джеймс Клерк|Максвелл]] использовал компактную кватернионную запись для формулировки [[Уравнения Максвелла|своих уравнений]] электромагнитного поля.<ref>''А. Н. Крылов'' [http://vivovoco.astronet.ru/VV/PAPERS/BIO/KRYLOV/KRYLOV_23.HTM Отзыв о работах академика П. П. Лазарева.]</ref> Позднее на основе алгебры кватернионов был создан трёхмерный [[векторный анализ]] ([[Гиббс, Джозайя Уиллард|Гиббс]], [[Хевисайд, Оливер|Хевисайд]]). |
Развитие кватернионов и их приложений в физике следовало по трём путям, связанным с алгебраическим подходом, апологетами которого выступали [[Кэли, Артур|Кэли]], который в 1858 году открыл матричное представление кватернионов{{sfn|Stillwell|2008|p=10}}, [[Клиффорд, Уильям Кингдон|Клиффорд]], [[Пирс, Бенджамин|Б. Пирс]], [[Пирс, Чарльз Сандерс|Ч. Пирс]] и Фробениус; с теорией комплексных кватернионов, представителями которого были Клиффорд, [[Штуди, Эдуард|Штуди]] и [[Котельников, Александр Петрович|Котельников]]; с физикой из-за имён Максвелла и Хэвисайда{{sfn|Березин, Курочкин и Толкачёв|2003|с=6—8}}. Несмотря на необычные свойства новых чисел (их некоммутативность), эта модель довольно быстро принесла практическую пользу. [[Максвелл, Джеймс Клерк|Максвелл]] использовал компактную кватернионную запись для формулировки [[Уравнения Максвелла|своих уравнений]] электромагнитного поля.<ref>''А. Н. Крылов'' [http://vivovoco.astronet.ru/VV/PAPERS/BIO/KRYLOV/KRYLOV_23.HTM Отзыв о работах академика П. П. Лазарева.] {{Wayback|url=http://vivovoco.astronet.ru/VV/PAPERS/BIO/KRYLOV/KRYLOV_23.HTM |date=20170503043859 }}</ref> Позднее на основе алгебры кватернионов был создан трёхмерный [[векторный анализ]] ([[Гиббс, Джозайя Уиллард|Гиббс]], [[Хевисайд, Оливер|Хевисайд]]){{sfn|Березин, Курочкин и Толкачёв|2003|с=8}}. Применение кватернионов было вытеснено векторным анализом из уравнений электродинамики. Впрочем тесная связь уравнений Максвелла с кватернионами не исчерпывается только электродинамикой, поскольку была построена теория СТО с использованием кватернионов {{нп3|Конвей, Артур Уильям|А. У. Конвеем|en|Arthur William Conway}} и {{нп3|Зильберштейн, Людвиг|Зильберштейном|pl|Ludwik Silberstein}}{{sfn|Березин, Курочкин и Толкачёв|2003|с=9}}. Послевоенный период применения кватернионов в физике связан с широким применением теории групп и их представлений в физике элементарных частиц. Также возможно заменить стандартное гильбертово пространство квантовой механики на его определение над телом кватернионов{{sfn|Березин, Курочкин и Толкачёв|2003|с=10}}. |
||
== Современное применение == |
== Современное применение == |
||
В XX |
В XX веке были сделаны несколько попыток использовать кватернионные модели в [[квантовая механика|квантовой механике]]<ref>{{книга|автор=Курочкин Ю. А. |заглавие=Кватернионы и некоторые приложения их в физике. Препринт диссертации № 109|издание=ИФ АН БССР |год=1976}}</ref> и [[теория относительности|теории относительности]]<ref name=ALEX>{{книга|автор=Александрова Н. В. |часть=Исчисление кватернионов Гамильтона |заглавие=''Гамильтон У. Р.'' Избранные труды: оптика, динамика, кватернионы |издательство=Наука |место=М. |год=1994 |серия=Классики науки}}— С. 519—534.</ref>. Реальное применение кватернионы нашли в современной [[компьютерная графика|компьютерной графике и программировании игр]]<ref>{{книга|автор=Побегайло А. П.|заглавие=Применение кватернионов в компьютерной геометрии и графике|место=Минск|издательство=Издательство БГУ |год=2010 |страниц=216 |isbn=978-985-518-281-9 }}.</ref>, а также в [[вычислительная механика|вычислительной механике]]<ref name="wittenburg">{{книга|автор=Виттенбург Й.|заглавие=Динамика систем твёрдых тел|место=М.|издательство=Мир|год=1980|страниц=292}} — С. 25—26, 34—36.</ref><ref name="pogorelov">{{книга|автор=Погорелов Д. Ю.|заглавие=Введение в моделирование динамики систем тел|место=Брянск|издательство=Издательство БГТУ|год=1997|страниц=156|isbn=5-230-02435-6}}. — С. 22—26, 31—36.</ref>, в [[инерциальная навигация|инерциальной навигации]] и [[теория управления|теории управления]]<ref>{{книга|автор=[[Ишлинский, Александр Юльевич|Ишлинский А. Ю.]]|заглавие=Ориентация, гироскопы и инерциальная навигация|место=М.|издательство=Наука|год=1976|страниц=672}} — С. 87—103, 593—604.</ref><ref>{{cite web|url=http://hypercomplex.xpsweb.com/articles/366/ru/pdf/07-10.pdf|title=Уравнения инерциальной навигации и кватернионная теория пространства-времени|last=Чуб В. Ф.|accessdate=2013-12-09|archive-date=2013-12-13|archive-url=https://web.archive.org/web/20131213142532/http://hypercomplex.xpsweb.com/articles/366/ru/pdf/07-10.pdf|deadlink=no}}</ref>. С 2003 года издаётся журнал «Гиперкомплексные числа в геометрии и физике»<ref>{{Cite web |url=http://hypercomplex.xpsweb.com/section.php?lang=ru&genre=3 |title=Журнал «Гиперкомплексные числа в геометрии и физике» |access-date=2014-03-13 |archive-date=2016-09-26 |archive-url=https://web.archive.org/web/20160926203312/http://hypercomplex.xpsweb.com/section.php?lang=ru&genre=3 |deadlink=no }}</ref>. |
||
Во многих областях применения были найдены более общие и практичные средства, чем кватернионы. Например, в наши дни для исследования движений в пространстве чаще всего применяется [[Матрица (математика)|матричное исчисление]]<ref>{{книга |автор=[[Клейн, Феликс|Клейн Ф.]] |заглавие=Лекции о развитии математики в XIX столетии |ссылка=http://www.math.ru/lib/book/djvu/klassik/razvitie.djvu |том=I |издательство=ГОНТИ |место=М.-Л. |год=1937 |страницы=229—231. |страниц=432}}</ref>. Однако там, где важно задавать трёхмерный поворот при помощи ''минимального'' числа скалярных параметров, использование [[параметры Родрига — Гамильтона|параметров Родрига — Гамильтона]] (то есть четырёх компонент кватерниона поворота) весьма часто оказывается предпочтительным: такое описание никогда не вырождается, а при описании поворотов тремя параметрами (например, [[углы Эйлера|углами Эйлера]]) всегда существуют критические значения этих параметров, когда описание вырождается<ref name="wittenburg" /><ref name="pogorelov" />. |
Во многих областях применения были найдены более общие и практичные средства, чем кватернионы. Например, в наши дни для исследования движений в пространстве чаще всего применяется [[Матрица (математика)|матричное исчисление]]<ref>{{книга |автор=[[Клейн, Феликс|Клейн Ф.]] |заглавие=Лекции о развитии математики в XIX столетии |ссылка=http://www.math.ru/lib/book/djvu/klassik/razvitie.djvu |том=I |издательство=ГОНТИ |место=М.-Л. |год=1937 |страницы=229—231. |страниц=432 |archivedate=2013-12-06 |archiveurl=https://web.archive.org/web/20131206192959/http://www.math.ru/lib/book/djvu/klassik/razvitie.djvu }}</ref>. Однако там, где важно задавать трёхмерный поворот при помощи ''минимального'' числа скалярных параметров, использование [[параметры Родрига — Гамильтона|параметров Родрига — Гамильтона]] (то есть четырёх компонент кватерниона поворота) весьма часто оказывается предпочтительным: такое описание никогда не вырождается, а при описании поворотов тремя параметрами (например, [[углы Эйлера|углами Эйлера]]) всегда существуют критические значения этих параметров, когда описание вырождается<ref name="wittenburg" /><ref name="pogorelov" />. |
||
Как алгебра над <math>\scriptstyle\ |
Как алгебра над <math>\scriptstyle\mathbb R</math>, кватернионы образуют вещественное векторное пространство <math>\scriptstyle\mathbb H</math>, снабжённое [[тензор]]ом третьего ранга <math>S</math> типа (1,2), иногда называемого ''структурным тензором''. Как всякий тензор такого типа, <math>S</math> отображает каждую [[Внешняя форма|1-форму]] <math>t</math> на <math>\scriptstyle\mathbb H</math> и пару векторов <math>\left(a, b\right)</math> из <math>\scriptstyle\mathbb H</math> в вещественное число <math>S\left(t, a, b\right)</math>. Для любой фиксированной 1-формы <math>t</math> <math>S</math> превращается в ковариантный тензор второго ранга, который, в случае его симметрии, становится [[Скалярное произведение|скалярным произведением]] на <math>\mathbb H</math>. Поскольку каждое вещественное векторное пространство является также вещественным [[Линейное многообразие|линейным многообразием]], такое скалярное произведение порождает тензорное поле, которое, при условии его невырожденности, становится (псевдо- или собственно-)евклидовой [[Метрика (дифференциальная геометрия)|метрикой]] на <math>\mathbb H</math>. В случае кватернионов это скалярное произведение [[Индефинитное произведение|индефинитно]], его [[Сигнатура (математика)|сигнатура]] не зависит от 1-формы <math>t</math>, а соответствующая псевдоевклидова метрика есть [[метрика Минковского]]<ref>''Vladimir Trifonov'' A Linear Solution of the Four-Dimensionality Problem // Euruphysics Letters, — IOP Publishing, V. 32, № 8 / 12.1995. — С. 621—626 — DOI: 10.1209/0295-5075/32/8/001.</ref>. Эта метрика автоматически продолжается на [[Группа Ли|группу Ли]] ненулевых кватернионов вдоль её левоинвариантных векторных полей, образуя так называемую закрытую ФЛРУ (Фридман — Леметр — Робертсон — Уолкер) метрику<ref>''Vladimir Trifonov'' Natural Geometry of Nonzero Quaternions // International Journal of Theoretical Physics, — Springer Netherlands, V. 46, № 2 / 02.2007. — С. 251—257 — ISSN 0020-7748 (Print) ISSN 1572-9575 (Online).</ref> — важное решение уравнений Эйнштейна. Эти результаты проясняют некоторые аспекты проблемы совместимости [[Квантовая механика|квантовой механики]] и [[ОТО|общей теории относительности]] в рамках теории [[Квантовая гравитация|квантовой гравитации]]<ref>''Vladimir Trifonov'' GR-Friendly Description of Quantum Systems // International Journal of Theoretical Physics, — Springer Netherlands, V. 47, № 2 / 02.2008. — С. 492—510 — ISSN 0020-7748 (Print) ISSN 1572-9575 (Online).</ref>. |
||
== См. также == |
== См. также == |
||
* [[Кватернионы и вращение пространства]] |
* [[Кватернионы и вращение пространства]] |
||
* [[Кватернионный анализ]] |
* [[Кватернионный анализ]] |
||
* [[Октонионы]] |
|||
* [[Октавы (алгебра)|Октавы]] |
|||
* [[Теорема Фробениуса]] |
* [[Теорема Фробениуса]] |
||
* [[Складывание рамок]] |
|||
* [[Шарнирный клин]] |
|||
== Примечания == |
== Примечания == |
||
| Строка 394: | Строка 469: | ||
== Литература == |
== Литература == |
||
;на русском языке |
|||
* ''И. Л. Кантор, А. С. Солодовников'' [http://www.ftl.kherson.ua/index.php?option=com_remository&Itemid=5&func=showdown&id=8026 Гиперкомплексные числа]. — {{М}}: [[Наука (издательство)|Наука]], 1973. — 144 с. |
|||
* {{книга|автор=Березин А. В., Курочкин Ю. А., Толкачёв Е. А.|часть=|заглавие=Кватернионы в релятивистской физике|оригинал=|ссылка=https://archive.org/details/isbn_5354004039|издание=2-е|ответственный=|место=М.|издательство=Едиториал УРСС|год=2003|том=|страницы=[https://archive.org/details/isbn_5354004039/page/n10 12]|страниц=202|isbn=5-354-00403-9|ref=Березин, Курочкин и Толкачёв}} |
|||
* ''Мищенко А., Соловьев Ю.'' [http://kvant.mccme.ru/1983/09/kvaterniony.htm Кватернионы], — [[Квант (журнал)|Квант]], N9, 1983. |
|||
* {{статья|автор=Ватульян А. О.|заглавие=Кватернионы|издание=[[Соросовский образовательный журнал]]|год=1999|номер=5|страницы=117—120 |ссылка=http://www.pereplet.ru/nauka/Soros/pdf/9905_117.pdf}} |
|||
* ''Martin John Baker'' [http://www.euclideanspace.com/maths/algebra/realNormedAlgebra/quaternions/index.htm EuclideanSpace.com] — применение кватернионов в 3D графике. |
|||
* {{книга |автор=Кантор И. Л., Солодовников А. С.|ссылка=https://studizba.com/uploads/unziped/real/246967/pdf/77557-66098.pdf |заглавие=Гиперкомплексные числа |место={{М}} |издательство=[[Наука (издательство)|Наука]] |год=1973 |страниц=144}} |
|||
* [https://web.archive.org/web/20041120030005/http://quater1.narod.ru/glava_II.pdf Кватернионы. Кватеры.] |
* [https://web.archive.org/web/20041120030005/http://quater1.narod.ru/glava_II.pdf Кватернионы. Кватеры.] |
||
* {{книга |автор=[[Конвей, Джон Хортон|Конвей Д.]], Смит Д.|заглавие=О кватернионах и октавах: об их геометрии, арифметике и симметриях |место={{М}} |издательство=[[МЦНМО]] |год=2009 |страниц=184 |ISBN=978-5-94057-517-7}} |
|||
* {{статья|автор=Ватульян А. О.|заглавие=Кватернионы|издание=[[Соросовский образовательный журнал]]|год=1999|номер=5|страницы= 117-120}} |
|||
* {{статья |автор = [[Мищенко, Александр Сергеевич|Мищенко А. С.]], Соловьёв Ю. П.|заглавие = Кватернионы|оригинал = |ссылка = http://kvant.mccme.ru/1983/09/kvaterniony.htm|издание = [[Квант (журнал)|Квант]]|год = 1983|том = 9|страницы = 10—15 |doi = |pmid = |bibcode = |arxiv = |ref = Мищенко и Соловьёв}} |
|||
* ''Джон Х.Конвей, Дерек А.Смит.'' О кватернионах и октавах: об их геометрии, арифметике и симметриях. - М.: МЦНМО, 2009. - 184 с. ISBN 978-5-94057-517-7 |
|||
;на других языках |
|||
* {{cite book | author=Stillwell, J. | year= 2008 | title=Naive lie theory | url=https://archive.org/details/naivelietheory0000stil | publisher=Springer | series=Undergraduate texts in mathematics | isbn=9780387782140|ref=Stillwell}} |
|||
* ''Martin John Baker'' [http://www.euclideanspace.com/maths/algebra/realNormedAlgebra/quaternions/index.htm EuclideanSpace.com] {{Wayback|url=http://www.euclideanspace.com/maths/algebra/realNormedAlgebra/quaternions/index.htm |date=20070927221021 }} — применение кватернионов в 3D графике. |
|||
{{вс}} |
|||
{{Числа}} |
{{Числа}} |
||
{{Алгебра над кольцом}} |
{{Алгебра над кольцом}} |
||
Текущая версия от 09:48, 28 сентября 2024
| Кватернион | |
|---|---|
| Дата основания, создания, возникновения | 1843[1] |
| Предыдущее по порядку | комплексное число |
| Следующее по порядку | Алгебра Кэли |
| Первооткрыватель или изобретатель | Уильям Роуэн Гамильтон[1] |
| Дата открытия (изобретения) | 1843 |
| Определяющая формула | |
| Обозначение в формуле | , и |
 | |
 | |
Кватернио́ны (от лат. quaterni, по четыре) — система гиперкомплексных чисел, образующая векторное пространство размерностью четыре над полем вещественных чисел. Обычно обозначаются символом . Предложены Уильямом Гамильтоном в 1843 году.
Кватернионы удобны для описания изометрий трёх- и четырёхмерного евклидовых пространств и поэтому получили широкое распространение в механике. Также их используют в вычислительной математике — например, при создании трёхмерной графики[2].
Анри Пуанкаре писал о кватернионах: «Их появление дало мощный толчок развитию алгебры; исходя от них, наука пошла по пути обобщения понятия числа, придя к концепциям матрицы и линейного оператора, пронизывающим современную математику. Это была революция в арифметике, подобная той, которую сделал Лобачевский в геометрии»[3].
Определения
[править | править код]Стандартное
[править | править код]Кватернионы можно определить как сумму
где — вещественные числа

- — мнимые единицы со следующим свойством: , при этом результат их попарного произведения зависит от порядка следования (не является коммутативным): , a .
| X | 1 | i | j | k |
|---|---|---|---|---|
| 1 | 1 | i | j | k |
| i | i | -1 | k | -j |
| j | j | -k | -1 | i |
| k | k | j | -i | -1 |
Как вектор и скаляр
[править | править код]Кватернион представляет собой пару где — вектор трёхмерного пространства, а — скаляр, то есть вещественное число.
Операции сложения определены следующим образом:
Произведение определяется следующим образом:
где обозначает скалярное произведение, а — векторное произведение.
В частности:
Заметим, что:
- Алгебраические операции в кватернионах обладают свойством дистрибутивности;
- Антикоммутативность векторного произведения влечёт некоммутативность произведения кватернионов.
Через комплексные числа
[править | править код]Произвольный кватернион можно представить как пару комплексных чисел в виде
или эквивалентно
где — комплексные числа, поскольку выполняется как для комплексных чисел, так и для кватернионов, а .
Через матричные представления
[править | править код]Вещественными матрицами
[править | править код]Кватернионы также можно определить как вещественные матрицы следующего вида с обычными матричными произведением и суммой:
При такой записи:
- сопряжённому кватерниону соответствует транспонированная матрица:
- ;
- четвёртая степень модуля кватерниона равна определителю соответствующей матрицы:
Комплексными матрицами
[править | править код]Альтернативно, кватернионы можно определить как комплексные матрицы следующего вида с обычными матричными произведением и суммой[4]:
здесь и обозначают комплексно-сопряжённые числа к и .
Такое представление имеет несколько замечательных свойств:
- комплексному числу соответствует диагональная матрица;
- сопряжённому кватерниону соответствует сопряжённая транспонированная матрица:
- ;
- квадрат модуля кватерниона равен определителю соответствующей матрицы:
Связанные объекты и операции
[править | править код]Для кватерниона
кватернион называется скалярной частью а кватернион — векторной частью. Если то кватернион называется чисто скалярным, а при — чисто векторным.
Сопряжение
[править | править код]Для кватерниона сопряжённым называется[5]:
Сопряжённое произведение есть произведение сопряжённых в обратном порядке[6]:
Для кватернионов справедливо равенство
Модуль
[править | править код]Так же, как и для комплексных чисел[7],
называется модулем . Если то называется единичным кватернионом.
В качестве нормы кватерниона обычно рассматривают его модуль: .
Таким образом, на множестве кватернионов можно ввести метрику. Кватернионы образуют метрическое пространство, изоморфное с евклидовой метрикой.
Кватернионы с модулем в качестве нормы образуют банахову алгебру.
Из тождества четырёх квадратов вытекает, что иными словами, кватернионы обладают мультипликативной нормой и образуют ассоциативную алгебру с делением.
Обращение умножения (деление)
[править | править код]Кватернион, обратный по умножению к , вычисляется так[5]: .
Алгебраические свойства
[править | править код]Множество кватернионов является примером тела, то есть кольца с делением и единицей. Множество кватернионов образует четырёхмерную ассоциативную алгебру с делением над полем вещественных (но не комплексных) чисел.
По теореме Фробениуса тела , , являются единственными конечномерными ассоциативными алгебрами с делением над полем вещественных чисел.
Некоммутативность умножения кватернионов приводит к неожиданным последствиям. Например, количество различных корней полиномиального уравнения над множеством кватернионов может быть больше, чем степень уравнения. В частности, уравнение имеет бесконечно много решений — это все единичные чисто векторные кватернионы.
Четыре базисных кватерниона и четыре противоположных им по знаку образуют по умножению группу кватернионов (порядка 8). Обозначается:
Кватернионы и повороты пространства
[править | править код]
Кватернионы, рассматриваемые как алгебра над , образуют четырёхмерное вещественное векторное пространство. Любой поворот этого пространства относительно может быть записан в виде , где и — пара единичных кватернионов, при этом пара определяется с точностью до знака, то есть один поворот определяют в точности две пары — и . Из этого следует, что группа Ли поворотов есть факторгруппа , где обозначает мультипликативную группу единичных кватернионов.
Чисто векторные кватернионы образуют трёхмерное вещественно векторное пространство. Любой поворот пространства чисто векторных кватернионов относительно может быть записан в виде , где — некоторый единичный кватернион. Соответственно, , в частности, диффеоморфно .
«Целые» кватернионы
[править | править код]В качестве нормы кватерниона выберем квадрат его модуля: .
Целыми по Гурвицу принято называть кватернионы такие, что все — целые и одинаковой чётности.
Целый кватернион называется
- чётным
- нечётным
- простым
если таким же свойством обладает его норма.
Целый кватернион называется примитивным, если он не делится ни на какое натуральное число, кроме , нацело (иными словами, ).
Целые единичные кватернионы
[править | править код]Существует 24 целых единичных кватерниона:
- ; ; ; ;
Они образуют группу по умножению, лежат в вершинах правильного 4-мерного многогранника — 3-кубооктаэдра (не путать с 3-мерным многогранником-кубооктаэдром).
Разложение на простые сомножители
[править | править код]Для примитивных кватернионов верен аналог основной теоремы арифметики.
Теорема.[8] Для любого фиксированного порядка множителей в разложении нормы кватерниона в произведение простых целых положительных чисел существует разложение кватерниона в произведение простых кватернионов такое, что . Причём данное разложение единственно по модулю домножения на единицы — это значит, что любое другое разложение будет иметь вид
- ,
где , , , … — целые единичные кватернионы.
Например, примитивный кватернион имеет норму 60, значит, по модулю домножения на единицы он имеет ровно 12 разложений в произведение простых кватернионов, отвечающих 12 разложениям числа 60 в произведений простых:
Общее число разложений такого кватерниона равно
Функции кватернионного переменного
[править | править код]Вспомогательные функции
[править | править код]Знак кватерниона вычисляется так:
Аргумент кватерниона — это угол в четырёхмерном пространстве между кватернионом и вещественной единицей:
В дальнейшем используется представление заданного кватерниона в виде
Здесь — вещественная часть кватерниона, . При этом , поэтому проходящая через и вещественную прямую плоскость имеет структуру алгебры комплексных чисел, что позволяет перенести на случай кватернионов произвольные аналитические функции. Они удовлетворяют стандартным соотношениям, если все аргументы имеют вид для фиксированного единичного вектора . В случае если требуется рассматривать кватернионы с разным направлением, формулы значительно усложняются, в силу некоммутативности алгебры кватернионов.
Элементарные функции
[править | править код]Стандартное определение аналитических функций на ассоциативной нормированной алгебре основано на разложении этих функций в степенные ряды. Рассуждения, доказывающие корректность определения таких функций, полностью аналогичны комплексному случаю и основаны на вычислении радиуса сходимости соответствующих степенных рядов. Учитывая указанное выше «комплексное» представление для заданного кватерниона, соответствующие ряды можно привести к указанной ниже компактной форме. Здесь приведены лишь некоторые наиболее употребительные аналитические функции, аналогично можно вычислить любую аналитическую функцию. Общее правило таково: если для комплексных чисел, то , где кватернион рассматривается в «комплексном» представлении .
- Степень и логарифм
Отметим, что, как обычно в комплексном анализе, логарифм оказывается определён лишь с точностью до .
- Тригонометрические функции
Линейное отображение
[править | править код]Отображение алгебры кватернионов называется линейным, если верны равенства
где — поле действительных чисел. Если является линейным отображением алгебры кватернионов, то для любых отображение
является линейным отображением. Если — тождественное отображение (), то для любых мы можем отождествить тензорное произведение с отображением
Для любого линейного отображения существует тензор , , такой, что
В приведённых выше равенствах предполагается суммирование по индексу . Поэтому мы можем отождествить линейное отображение и тензор .
Регулярные функции
[править | править код]Существуют разные способы определения регулярных функций кватернионного переменного. Самый явный — рассмотрение кватернионно дифференцируемых функций, при этом можно рассматривать праводифференцируемые и леводифференцируемые функции, не совпадающие в силу некоммутативности умножения кватернионов. Очевидно, что их теория полностью аналогична. Определим кватернионно леводифференцируемую функцию как имеющую предел
Оказывается, что все такие функции имеют в некоторой окрестности точки вид
где — постоянные кватернионы. Другой способ основан на использовании операторов
и рассмотрении таких кватернионных функций , для которых[9]
что полностью аналогично использованию операторов и в комплексном случае. При этом получаются аналоги интегральной теоремы Коши, теории вычетов, гармонических функций и рядов Лорана для кватернионных функций[10].
Дифференцирование отображений
[править | править код]Непрерывное отображение называется дифференцируемым на множестве , если в каждой точке изменение отображения может быть представлено в виде
где
линейное отображение алгебры кватернионов и такое непрерывное отображение, что
Линейное отображение называется производной отображения .
Производная может быть представлена в виде[11]
Соответственно дифференциал отображения имеет вид
Здесь предполагается суммирование по индексу . Число слагаемых зависит от выбора функции . Выражения и называются компонентами производной.
Для произвольного кватерниона верно равенство
Виды умножений
[править | править код]Умножение Грассмана
[править | править код]Так по-другому называется общепринятое умножение кватернионов ().
Евклидово умножение
[править | править код]Отличается от общепринятого тем, что вместо первого сомножителя берётся сопряжённый к нему: . Оно также некоммутативно.
Скалярное произведение
[править | править код]Аналогично одноимённой операции для векторов:
- .
Эту операцию можно использовать для выделения одного из коэффициентов, например, .
Определение модуля кватерниона можно видоизменить:
- .
Внешнее произведение
[править | править код]- .
Используется не очень часто, тем не менее рассматривается в дополнение к скалярному произведению.
Векторное произведение
[править | править код]Аналогично одноимённой операции для векторов. Результатом является тоже вектор:
- .
Из истории
[править | править код]
Система кватернионов была впервые опубликована Гамильтоном в 1843 году. Историки науки также обнаружили наброски по этой теме в неопубликованных рукописях Гаусса, относящихся к 1819—1820 годам[13]. Также кватернионы рассматривал Эйлер. Б. О. Родриг (1840 год) при рассмотрении поворотов абсолютно твёрдого тела вывел правила умножения кватернионов[14][15].
Бурное и чрезвычайно плодотворное развитие комплексного анализа в XIX веке стимулировало у математиков интерес к следующей задаче: найти новый вид чисел, аналогичный по свойствам комплексным, но содержащий не одну, а две мнимые единицы. Предполагалось, что такая модель будет полезна при решении пространственных задач математической физики. Однако работа в этом направлении оказалась безуспешной[15].
Новый вид чисел был обнаружен ирландским математиком Уильямом Гамильтоном (который также занимался указанной задачей) в 1843 году, и он содержал не две, как ожидалось, а три мнимые единицы. Гамильтон работал сначала с дуплетами (точками на плоскости) и легко получил правила для умножения соответствующие комплексным числам, но для точек в пространстве (триплеты) не мог получить никакой формулы умножения для таких наборов. В конце концов решил попробовать четвёрки — точки в четырёхмерном пространстве. Эти числа Гамильтон назвал кватернионами[16]. Позднее Фробениус строго доказал (1877) теорему, согласно которой расширить комплексное поле до поля или тела с двумя мнимыми единицами невозможно[17].
Развитие кватернионов и их приложений в физике следовало по трём путям, связанным с алгебраическим подходом, апологетами которого выступали Кэли, который в 1858 году открыл матричное представление кватернионов[6], Клиффорд, Б. Пирс, Ч. Пирс и Фробениус; с теорией комплексных кватернионов, представителями которого были Клиффорд, Штуди и Котельников; с физикой из-за имён Максвелла и Хэвисайда[18]. Несмотря на необычные свойства новых чисел (их некоммутативность), эта модель довольно быстро принесла практическую пользу. Максвелл использовал компактную кватернионную запись для формулировки своих уравнений электромагнитного поля.[19] Позднее на основе алгебры кватернионов был создан трёхмерный векторный анализ (Гиббс, Хевисайд)[20]. Применение кватернионов было вытеснено векторным анализом из уравнений электродинамики. Впрочем тесная связь уравнений Максвелла с кватернионами не исчерпывается только электродинамикой, поскольку была построена теория СТО с использованием кватернионов А. У. Конвеем[англ.] и Зильберштейном[пол.][21]. Послевоенный период применения кватернионов в физике связан с широким применением теории групп и их представлений в физике элементарных частиц. Также возможно заменить стандартное гильбертово пространство квантовой механики на его определение над телом кватернионов[22].
Современное применение
[править | править код]В XX веке были сделаны несколько попыток использовать кватернионные модели в квантовой механике[23] и теории относительности[24]. Реальное применение кватернионы нашли в современной компьютерной графике и программировании игр[25], а также в вычислительной механике[26][27], в инерциальной навигации и теории управления[28][29]. С 2003 года издаётся журнал «Гиперкомплексные числа в геометрии и физике»[30].
Во многих областях применения были найдены более общие и практичные средства, чем кватернионы. Например, в наши дни для исследования движений в пространстве чаще всего применяется матричное исчисление[31]. Однако там, где важно задавать трёхмерный поворот при помощи минимального числа скалярных параметров, использование параметров Родрига — Гамильтона (то есть четырёх компонент кватерниона поворота) весьма часто оказывается предпочтительным: такое описание никогда не вырождается, а при описании поворотов тремя параметрами (например, углами Эйлера) всегда существуют критические значения этих параметров, когда описание вырождается[26][27].
Как алгебра над , кватернионы образуют вещественное векторное пространство , снабжённое тензором третьего ранга типа (1,2), иногда называемого структурным тензором. Как всякий тензор такого типа, отображает каждую 1-форму на и пару векторов из в вещественное число . Для любой фиксированной 1-формы превращается в ковариантный тензор второго ранга, который, в случае его симметрии, становится скалярным произведением на . Поскольку каждое вещественное векторное пространство является также вещественным линейным многообразием, такое скалярное произведение порождает тензорное поле, которое, при условии его невырожденности, становится (псевдо- или собственно-)евклидовой метрикой на . В случае кватернионов это скалярное произведение индефинитно, его сигнатура не зависит от 1-формы , а соответствующая псевдоевклидова метрика есть метрика Минковского[32]. Эта метрика автоматически продолжается на группу Ли ненулевых кватернионов вдоль её левоинвариантных векторных полей, образуя так называемую закрытую ФЛРУ (Фридман — Леметр — Робертсон — Уолкер) метрику[33] — важное решение уравнений Эйнштейна. Эти результаты проясняют некоторые аспекты проблемы совместимости квантовой механики и общей теории относительности в рамках теории квантовой гравитации[34].
См. также
[править | править код]- Кватернионы и вращение пространства
- Кватернионный анализ
- Октонионы
- Теорема Фробениуса
- Складывание рамок
Примечания
[править | править код]- ↑ 1 2 Hazewinkel M., Gubareni N. M., (not translated to en) Algebras, rings and modules (англ.) — Springer Science+Business Media, 2004. — P. 12. — ISBN 978-1-4020-2690-4
- ↑ Кватернионы в программировании игр Архивная копия от 25 июля 2009 на Wayback Machine (GameDev.ru)
- ↑ Полак Л. С. Уильям Роуэн Гамильтон (к 150-летию со дня рождения) // Труды Института истории естествознания. — АН СССР, 1956. — Т. 15 (История физ.-мат. наук). — С. 273..
- ↑ Stillwell, 2008, p. 7.
- ↑ 1 2 Stillwell, 2008, p. 9.
- ↑ 1 2 Stillwell, 2008, p. 10.
- ↑ Stillwell, 2008, p. 8.
- ↑ John C. Baez. On Quaternions and Octonions: Their Geometry, Arithmetic, and Symmetry, by John H. Conway and Derek A. Smith (англ.). — Review. Дата обращения: 7 февраля 2009. Архивировано 22 августа 2011 года.
- ↑ R. Fueter Über die analytische Darstellung der regulären Funktionen einer Quaternionenvariablen, — Comment. math. Helv. 8, pp.371—378, 1936.
- ↑ A. Sudbery Quaternionic Analysis, — Department of Mathematics, University of York, 1977.
- ↑ Выражение не является дробью и должно восприниматься как единый символ. Данное обозначение предложено для совместимости с обозначением производной. Значение выражения при заданном является кватернионом.
- ↑ В письме своему сыну Арчибальду от 5 августа 1865 года Гамильтон пишет: «…Но, конечно, надпись уже стёрлась» (Л. С. Полак Вариационные принципы механики, их развитие и применение в физике.— М.: Физматгиз, 1960.— С.103-104)
- ↑ Бурбаки Н.. Архитектура математики. Очерки по истории математики. — М.: Иностранная литература, 1963. — С. 68.
- ↑ Rodrigues Olinde. Геометрические законы, управляющие перемещениями твёрдой системы в пространстве, и изменение координат, возникающее в результате этих перемещений, рассматриваемые независимо от причин, которые могут их вызвать = Des lois géométriques qui régissent les déplacements d'un système solide dans l'espace, et de la variation des coordonnées provenant de ces déplacements considérés indépendamment des causes qui peuvent les produire // Journal de Mathématiques Pures et Appliquées. — 1840. — Т. 5. — С. 380—440.
- ↑ 1 2 Березин, Курочкин и Толкачёв, 2003, с. 5.
- ↑ Мищенко и Соловьёв, 1983, с. 11—12.
- ↑ Мищенко и Соловьёв, 1983, с. 15.
- ↑ Березин, Курочкин и Толкачёв, 2003, с. 6—8.
- ↑ А. Н. Крылов Отзыв о работах академика П. П. Лазарева. Архивная копия от 3 мая 2017 на Wayback Machine
- ↑ Березин, Курочкин и Толкачёв, 2003, с. 8.
- ↑ Березин, Курочкин и Толкачёв, 2003, с. 9.
- ↑ Березин, Курочкин и Толкачёв, 2003, с. 10.
- ↑ Курочкин Ю. А. Кватернионы и некоторые приложения их в физике. Препринт диссертации № 109. — ИФ АН БССР. — 1976.
- ↑ Александрова Н. В. Исчисление кватернионов Гамильтона // Гамильтон У. Р. Избранные труды: оптика, динамика, кватернионы. — М.: Наука, 1994. — (Классики науки).— С. 519—534.
- ↑ Побегайло А. П. Применение кватернионов в компьютерной геометрии и графике. — Минск: Издательство БГУ, 2010. — 216 с. — ISBN 978-985-518-281-9..
- ↑ 1 2 Виттенбург Й. Динамика систем твёрдых тел. — М.: Мир, 1980. — 292 с. — С. 25—26, 34—36.
- ↑ 1 2 Погорелов Д. Ю. Введение в моделирование динамики систем тел. — Брянск: Издательство БГТУ, 1997. — 156 с. — ISBN 5-230-02435-6.. — С. 22—26, 31—36.
- ↑ Ишлинский А. Ю. Ориентация, гироскопы и инерциальная навигация. — М.: Наука, 1976. — 672 с. — С. 87—103, 593—604.
- ↑ Чуб В. Ф. Уравнения инерциальной навигации и кватернионная теория пространства-времени. Дата обращения: 9 декабря 2013. Архивировано 13 декабря 2013 года.
- ↑ Журнал «Гиперкомплексные числа в геометрии и физике». Дата обращения: 13 марта 2014. Архивировано 26 сентября 2016 года.
- ↑ Клейн Ф. Лекции о развитии математики в XIX столетии. — М.—Л.: ГОНТИ, 1937. — Т. I. — С. 229—231.. — 432 с. Архивировано 6 декабря 2013 года.
- ↑ Vladimir Trifonov A Linear Solution of the Four-Dimensionality Problem // Euruphysics Letters, — IOP Publishing, V. 32, № 8 / 12.1995. — С. 621—626 — DOI: 10.1209/0295-5075/32/8/001.
- ↑ Vladimir Trifonov Natural Geometry of Nonzero Quaternions // International Journal of Theoretical Physics, — Springer Netherlands, V. 46, № 2 / 02.2007. — С. 251—257 — ISSN 0020-7748 (Print) ISSN 1572-9575 (Online).
- ↑ Vladimir Trifonov GR-Friendly Description of Quantum Systems // International Journal of Theoretical Physics, — Springer Netherlands, V. 47, № 2 / 02.2008. — С. 492—510 — ISSN 0020-7748 (Print) ISSN 1572-9575 (Online).
Литература
[править | править код]- на русском языке
- Березин А. В., Курочкин Ю. А., Толкачёв Е. А. Кватернионы в релятивистской физике. — 2-е. — М.: Едиториал УРСС, 2003. — С. 12. — 202 с. — ISBN 5-354-00403-9.
- Ватульян А. О. Кватернионы // Соросовский образовательный журнал. — 1999. — № 5. — С. 117—120.
- Кантор И. Л., Солодовников А. С. Гиперкомплексные числа. — М.: Наука, 1973. — 144 с.
- Кватернионы. Кватеры.
- Конвей Д., Смит Д. О кватернионах и октавах: об их геометрии, арифметике и симметриях. — М.: МЦНМО, 2009. — 184 с. — ISBN 978-5-94057-517-7.
- Мищенко А. С., Соловьёв Ю. П. Кватернионы // Квант. — 1983. — Т. 9. — С. 10—15.
- на других языках
- Stillwell, J. Naive lie theory. — Springer, 2008. — ISBN 9780387782140.
- Martin John Baker EuclideanSpace.com Архивная копия от 27 сентября 2007 на Wayback Machine — применение кватернионов в 3D графике.

























































































































![{\displaystyle {\frac {df}{dq}}=\lim _{h\to 0}\left[h^{-1}\left(f\left(q+h\right)-f\left(q\right)\right)\right]}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/bc96e5f4fcf7b74e526843c7c0affac5b73c9abe)










































